一种基于路网抗震韧性的路段重要度评价方法
陈轶钦, 黄淑萍
(上海交通大学 船舶海洋与建筑工程学院,上海 200240)
工程系统发展至今,呈现出高度复杂化与集成化的特点,系统内部构件与构件、子系统与子系统间相互联系、相互依赖,不可避免地增加了系统发生级联故障的隐患.识别重要构件可以降低级联故障的风险,提高系统的安全性,是工程系统安全的一大研究重点.
过去,工程系统的可靠性(reliability)、脆弱性(vulnerability)与鲁棒性(robustness)是主要研究方向,构件的重要度指标因而基于系统的可靠性/脆弱性/鲁棒性.以上3种属性互有差异,但都关注系统的灾前预防阶段,缺少对系统灾后恢复阶段的考虑.近几年来,韧性理论受到广泛关注,许多学者开始转向工程系统韧性的研究.韧性(resilience)是系统抵抗灾害事件干扰、恢复功能的能力,涉及自灾害发生至系统性能恢复的全过程,系统韧性的研究可以为系统灾前预防与灾后恢复策略提供重要的参考.
基于韧性的构件重要度指标的基本思想与基于可靠性、脆弱性的重要度指标类似,即构件重要度体现在构件的状态变化对系统的正面/负面影响.已有的文献多采用二态极值的原则,即考虑构件完好无损/完全损坏两个状态,以系统韧性的增加/减少值(Resilience Achievement/Reduction Worth,RAW/RRW)作为重要度指标[1-2].Li等[3]提出还可以将构件状态波动一定数值或一定比例下系统韧性的增加/减少值作为评价指标.
已有的文献多考虑灾害事件发生初始时刻时,构件处于完好无损/完全损坏对系统韧性的影响.Li等[3]考虑构件自t=0始终连通/中断时系统总体韧性的变化;Barker等[1]考虑构件的连通/中断对系统恢复时间的影响;潘星等[4]考虑构件t=0时刻中断时系统的RRW;Zhang等[5-6]基于构件t=0时刻的连通/中断,计算构件的结构重要度、冗余重要度和加固重要度.
具体到道路交通系统,识别重要构件一般指识别重要路段.目前,路段脆弱性重要度的研究较为丰富,而路段韧性重要度的研究较少,吕彪等[2]以路段自t=0时刻起始终中断/连通时不同时刻韧性的变化作为RRW/RAW,未考虑该路段的恢复过程;Gao等[7]以概率重要度和临界重要度评价不同时刻路段中断/连通时对系统连通韧性的影响程度,并以某时刻所评价路段的瞬时状态变化为假设.何祥等[8]采用扩展傅里叶振幅灵敏度检验(EFAST)方法提出了一种各路段基于不同韧性能力的重要度评价框架,分别评价路段的抵御、吸收和恢复能力对路网韧性的影响.
综观已有文献,本文认为目前构件/路段韧性重要度的研究主要存在两点不足.第一,已有多数研究仅以灾害发生初始时刻构件状态变化对系统韧性的影响来评价构件韧性重要度,评价结果不够全面.构件韧性重要度可能会随时间变化,因而不同时刻构件韧性重要度及其排序可能会与t=0时刻不同;此外,从定义来看,韧性是系统鲁棒性(灾前抵抗)与恢复性(灾后恢复)的综合体现,t=0时刻构件重要度只反映了构件的鲁棒性水平对系统韧性的影响.第二,已有的不同时刻路段韧性重要度研究考虑的是某时刻路段状态的瞬时变化对系统韧性的影响,实质上是一种将连续的系统韧性曲线在时间维度上离散化,每个时刻单独进行敏感性分析的方法,关注的是该时刻系统韧性的变化,不考虑该时刻路段状态的变化对其他时刻系统韧性的影响,缺少系统韧性的全过程变化视角.此外,仅单纯将具有连续时间属性的韧性在时间维度上离散化,不考虑不同时刻路段状态的变化对其他时刻系统韧性的影响,是基于维修短时或瞬时完成的假设,这与一般维修过程不符,实际维修并非瞬时完成,并对恢复系统韧性具有过程性的影响.因此,考虑由路段的维修过程而引起的系统韧性全过程变化更具有现实意义.
简而言之,目前大多数的研究基本思路沿袭了可靠性、脆弱性的构件/路段重要度识别,忽略了恢复过程在构件/路段重要度识别中的作用.对于构件/路段,初始状态与恢复过程都会影响其韧性重要度.因此,对于构件/路段韧性重要度的评价不能仅仅沿用可靠性、脆弱性研究的思路,只考虑瞬时状态的变化,而应考虑路段在不同恢复过程下的重要度变化.
贝叶斯网络(Bayesian Network,BN)因其直观表达变量间的关系、处理不确定性、信息融合等能力,是可靠性、脆弱性研究中应用较多的图论方法[9-10].BN能够以节点的观测数据为证据,结合先验条件概率表实现双向(向前、向后)推理,更新网络各节点的后验概率,适用于构件重要度的识别.作为BN的扩展,动态贝叶斯网络(Dynamic Bayesian Network,DBN)的优势在于直观表达变量时变特征的能力,其增加了时间维度,以跨时间片变量间的条件概率表征变量随时间的变化.BN双向推理实现的是某时刻观测节点的父节点与子节点的概率更新,而DBN双向推理实现的是观测节点的父节点与子节点的全过程时刻概率更新,能够同时反映系统韧性的两要素——抗震鲁棒性与震后恢复性的动态变化.
综上所述,以韧性的增加值RAW为评价指标,提出一种基于路网抗震韧性的路段重要度评价方法.此重要度评价方法重新定义并量化了不同时刻路段抗震韧性重要度,能够从震前预防和震后恢复两个视角指导路网抗震韧性水平的提升.对震前预防策略来说,需要重点关注t=0时刻重要度较高的路段,提高路段抗震鲁棒性,从韧性理论中的鲁棒性部分提高路网韧性水平;对震后恢复策略来说,需要合理分配维修资源,优先修复重要度对时间较敏感的路段,提高路段震后恢复性,从韧性理论中的恢复性部分提高路网韧性水平.
1 路网抗震韧性的量化模型
1.1 基于性能曲线的韧性函数
韧性是系统对干扰事件抵抗、恢复性能的能力,韧性函数是量化系统韧性的常用模型,其以系统性能随时间变化的曲线为基础.
一般来说,一次干扰事件发生后,系统性能会经历4个阶段,即灾前阶段、抵抗/破坏阶段、恢复阶段和恢复后阶段.Henry等[11]给出了普遍的系统受干扰事件影响的性能曲线,如图1所示.图中:F(t)为t时刻系统的性能;F(t0)为干扰事件发生前系统正常运行时的性能;F(td)为系统受干扰事件影响后的性能;F(tf)为系统恢复后的性能;S0为系统初始稳定状态;Sd为破坏状态;Sf为恢复后稳定状态;t0为初始时刻;te为干扰事件发生的起始时刻;td为干扰事件影响的结束时刻;ts为系统恢复的起始时刻;tf为系统恢复95%或100%初始稳定状态水平的时刻.

图1 干扰事件下的系统性能变化曲线
[te,tf]时间段系统性能曲线表达了系统自干扰事件发生起,抵抗干扰事件造成的负面影响,并逐渐恢复至原有或新稳定水平时性能随时间变化的特征.该时间段的性能曲线即为系统韧性量化的基础,应用韧性函数即可计算系统t时刻的韧性.韧性函数表示为系统性能曲线与横轴所围面积和系统正常运行时性能与横轴所围面积之比,表达式如下:
(1)
式中:R(t)为t时刻系统的韧性.
1.2 路网抗震性能之一——连通性
1.2.1路网的抗震功能组成 在地震发生后,可按照不同的功能将区域路网节点划分为三类——救援要害部门、人口密集区和区域对外出入口.其中,救援要害部门由政府部门、消防公安单位与医院组成;人口密集区由避灾疏散场所、社区与商业区组成;区域对外出入口由公路出入口、火车站、码头等组成.受灾区域路网承担的任务主要包括应急救援、物资运输和医疗救护,如图2所示.
应急救援、物资运输和医疗救护系统作为抗震功能的子系统,3个功能均有效时,路网的抗震功能被认为是有效的.因此,子系统的连通性共同决定了路网的连通性.
1.2.2路网抗震功能的连通逻辑 基于图2的内容并进行路网分析,路网抗震功能的连通逻辑如下:
(1) 路段—路径.路径上的每条路段都连通时,该条路径被认为是连通的,路段与路径的关系类似逻辑门中的“与门”.
(2) 路径—OD对.OD对所含路径至少有一条是连通时,该OD对被认为是连通的,路径与OD对的关系类似逻辑门中的“或门”.
(3)OD对—OD对中的O点/D点.与O点/D点组成的OD对中至少有一对是连通时,该O点/D点被认为是连通的,O点/D点与相应的OD对的关系类似逻辑门中的“或门”.
(4)O点/D点—抗震功能系统.抗震功能系统所含的每个O点/D点都连通时,该系统被认为是连通的,O点/D点与系统的关系类似逻辑门中的“与门”.
(5) 抗震功能系统—路网.路网的抗震功能分系统均连通时,该路网被认为是连通的,抗震功能系统与路网的关系类似逻辑门中的“与门”.
1.2.3路网连通性随时间的变化 基于上节的内容可以得到,路段的连通性共同决定了路网抗震功能的连通性,赋予路段连通性的时变特征能够推导路网连通性的时变特征.
假定维修速率不变,在维修过程中,路段状态的变化仅由上一时刻的状态决定,与之前时刻的状态无关,这一规律符合马尔可夫链.马尔可夫链是一种离散的马尔可夫过程,该过程中,在给定当前知识或信息的情况下,只有当前的状态用于预测将来,过去(即历史状态)对于预测未来(即当前之后的状态)是无关的.在马尔可夫链模型中,对象从一个状态变到另一个状态是遵循概率分布的.状态的改变称为“迁移”,与不同的状态改变相关的概率称为“状态迁移概率”.
在本文构建的路段状态的马尔可夫链中,路段状态分为“连通”与“中断”,状态迁移概率由维修速率决定.路段状态的迁移概率矩阵如表1所示.表中:λ=1/tMTTR,λ为维修速率,tMTTR为维修时间(Mean Time to Repair, MTTR)[12].

表1 路段状态的迁移矩阵
地震破坏时间相对于震后抢修时间非常短暂,假定地震灾害对系统的破坏是瞬时的,且道路抢修工作及时进行,即考虑图1中[ts,tf]时间段的连通性曲线量化评价路网的韧性.
2 基于路网抗震韧性的路段重要度评价方法
采用DBN表征路网抗震功能的连通逻辑及路段连通性随时间的变化,输出路网连通性时变曲线,应用韧性函数量化路网韧性曲线.借助DBN双向推理能力,以初始DBN为基准,不同时刻路段连通为证据,更新路网韧性曲线,计算韧性的增加值,评价不同时刻路段韧性重要度.评价方法技术路线如图3所示.
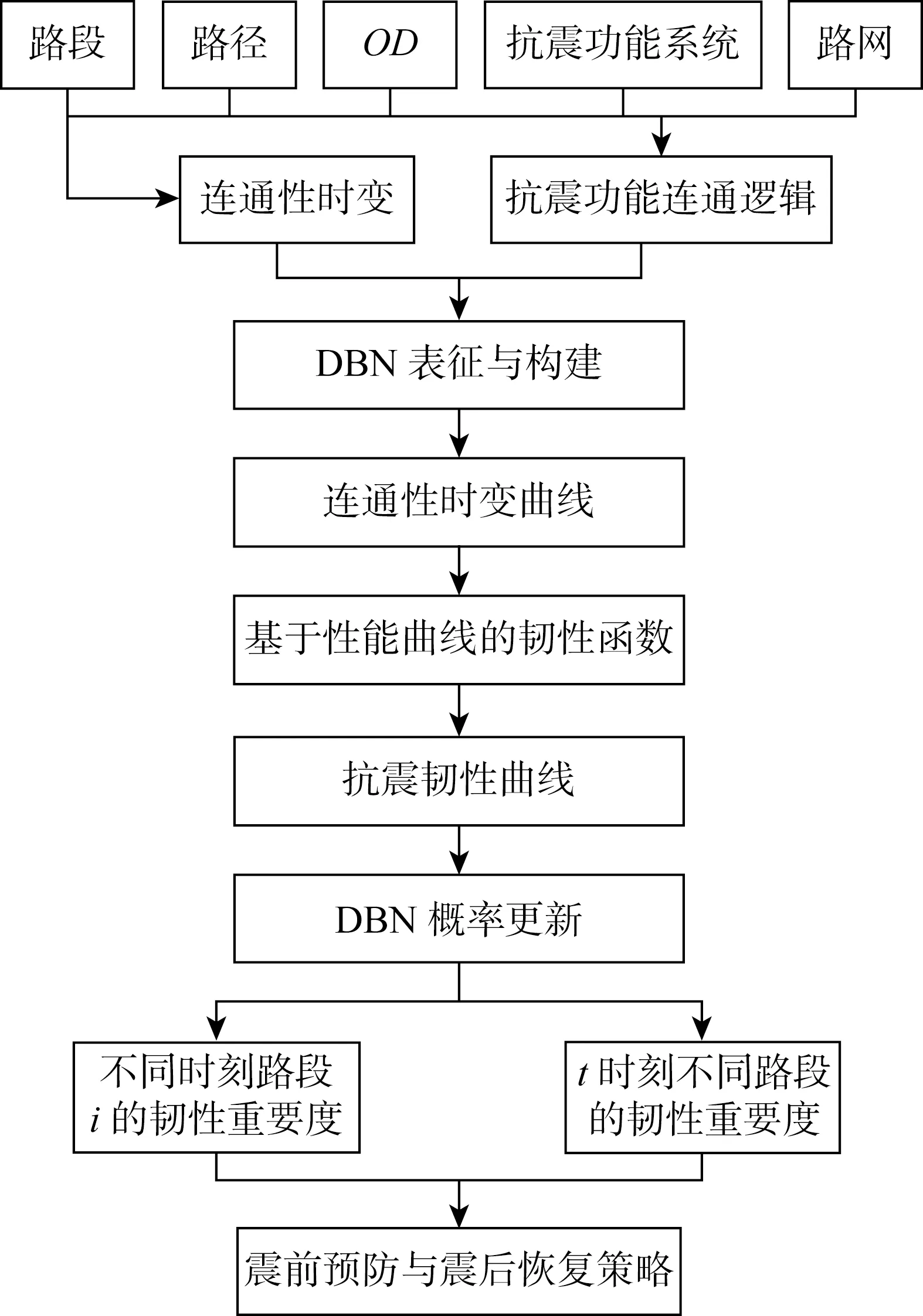
图3 评价方法技术路线图
2.1 基准DBN构建
本文构建的基准DBN如图4所示.其中,地震节点(烈度7、烈度8、烈度9)与恢复节点(7恢复速率、8度恢复速率、9度恢复速率)为三态节点,其余节点(中断、连通)均为二态节点.节点之间的边代表条件概率表(Conditioned Probability Table, CPT),反映节点的因果关系,表2给出了DBN中边的意义.

表2 DBN中边的意义

图4 路网动态贝叶斯网络结构示意图
构建动态贝叶斯网络模型的过程如图5所示.与BN模型构建类似, DBN的建模也需要先确定节点及各节点间的因果关系.而两者的不同之处在于,DBN建模还需确定各节点间在时间维度上是否存在因果关系,即BN模型的构建需要节点及各节点间的CPT,DBN模型在上述两个要素外还需各节点间跨时刻的CPT.
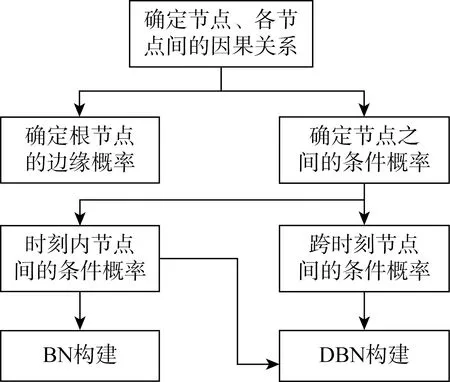
图5 动态贝叶斯网络建模过程
基于1.2节内容,可构建本文的基准DBN.其中,“路网的抗震功能组成”用于确定DBN中的节点,即“路段”“路径”“OD对”“O/D点”“抗震功能系统”和“路网”节点;“路网抗震功能的连通逻辑”用于确定时刻内节点间的条件概率;“路网连通性随时间的变化”用于确定跨时刻节点间的CPT,即不同时刻的“路段”节点之间的条件概率.
除此之外,构建的DBN中还有“地震”与“恢复”节点.“地震”节点为根节点,与“路段”节点的连通概率和“恢复”节点的恢复速率存在因果关系,影响路网初始时刻的连通性;“恢复”节点与“路段”节点的恢复过程存在因果关系,影响路网的连通性时变.“地震”节点的边缘概率由所考虑的烈度而定,评价何烈度下的路网韧性,即设置该烈度的发生概率为1.
CPT的来源较为广泛,可来自于调查问卷、模拟实验数据或专家访谈,本文的CPT则是基于客观数据进行设置,相对客观.其中,“地震”与“路段”节点间的CPT是基于震害数据并采用震害经验统计法计算得到的;时刻内各节点的CPT是基于路网分析得到的客观逻辑设置的;跨时刻节点间的CPT是基于表1路段状态的迁移矩阵设置的.因此,本文所构建的基准DBN较为客观、符合现实情况.
基于地震烈度的先验概率与节点间的条件概率表,可以计算每一时刻路网的连通性,输出连通性曲线,应用韧性函数即可得到路网的抗震韧性曲线.具体方法与过程可参考文献[13].
2.2 路段韧性重要度评价
2.2.1路网韧性重要度指标 本文基于韧性的内涵,将t时刻路段韧性重要度定义为:自t=0时刻起,至t时刻路段修复至连通时路网韧性的增加值.路段韧性重要度指标的表达式如下:
(2)

该路段韧性重要度指标是对已有路段韧性重要度指标[2,7]的一种改进.与仅考虑初始时刻路段处于完全中断/连通对路网韧性的影响作为重要度指标相比,本指标考虑了不同时刻路段恢复对路网韧性的影响;与考虑某时刻路段完全中断/连通对路网韧性的影响作为重要度指标相比,本指标考虑了路段的恢复过程对全过程路网韧性(即韧性曲线的变化)的影响.
如图6所示,传统路段韧性重要度指的是路段瞬时连通下该时刻系统韧性的增加值,韧性曲线在该时刻骤变;本文路段韧性重要度指的是路段在不同维修速率下基准时刻的系统韧性增加值,关注韧性曲线的全过程变化.

图6 路段韧性重要度对比
2.2.2路段韧性重要度评价 在基准DBN中添加t时刻路段i连通的证据后,DBN的向前推理能够更新节点(路段i节点自身、路段i节点的父节点与子节点)t时刻及以后的概率变化,向后推理能够更新节点初始时刻至t时刻的概率变化,实现路网韧性的全过程概率更新,如图7所示.将更新后的路网韧性与基准路网韧性代入式(2),即可评价路段韧性重要度.

图7 DBN的概率更新原理
本文提出的路段韧性重要度指标符合韧性的内涵,重要度评价方法能够指导区域路网灾前预防与灾后恢复策略.t=0时刻的路段韧性重要度反映了路段受地震作用依然保持连通条件下路网韧性的提高水平,符合韧性内涵中的鲁棒性部分,对应灾前预防工作;t>0时刻的路段韧性重要度反映了路段震后不同修复速率条件下路网韧性的提高水平,符合韧性内涵中的恢复性部分,对应灾后恢复工作.
3 实例应用
3.1 实例概况
选择青岛市市南区局部(八大湖、金门路、香港中路和珠海路4个街道)路网作为实例,验证本文提出的基于路网韧性的路段重要度评价方法的实用性.该路网的拓扑结构图包含17个节点、42条路段,如图8所示;不同烈度下路段的连通概率如表3所示,其为张洁[14]通过震害调查数据,结合震害经验统计法计算得到的客观结果;路段—路径—OD对—O点/D点—抗震功能系统的关联信息如表4所示.其中,应急救援/物资运输系统的连通指其所含的所有D点的连通,每个D点的连通表示每个汇点均有至少一个O点(救援部门/物资运输点)能够服务;医疗救护系统的连通指所含的所有O点的连通,每个O点的连通表示每个源点均有至少一个D点(医院)能够服务.
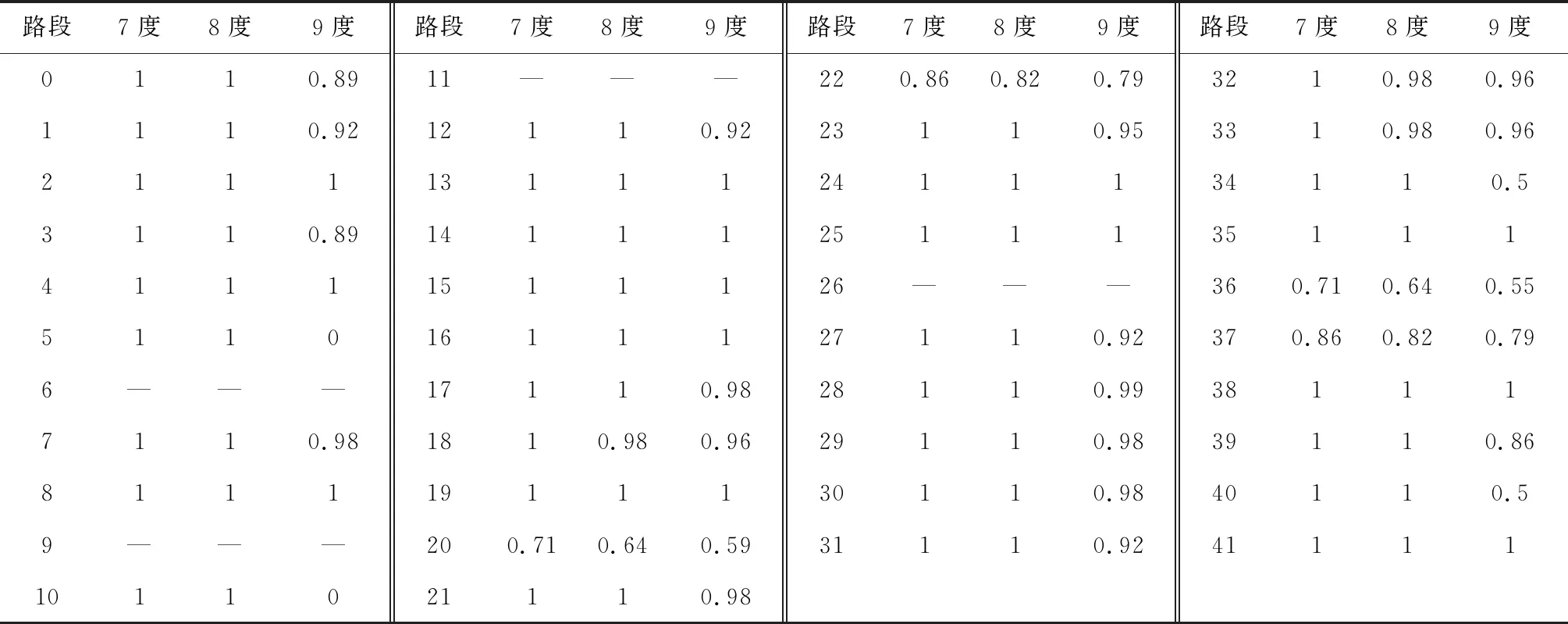
表3 不同烈度下路段的连通概率[14]

表4 抗震功能分系统下的OD对及路径

图8 路网拓扑结构图
方东平等[15]给出了不同烈度下各类交通功能完全恢复的平均时间,基于此,本文设定7度、8度、9度烈度下的恢复时间tMTTR=2, 5, 11 d.
3.2 基准DBN构建
基于上述实例信息与数据,构建路网的DBN.该DBN能够评价路网的全过程抗震韧性,同时也是评价路段韧性重要度的基准.
在7、8度烈度下,该路网的连通性始终为1,因而其韧性也为1,可能的原因是所选算例的设计抗震烈度高,路网7、8度烈度下性能未受损.因此本文关注9度烈度下该路网的连通性与抗震韧性,9度烈度下路网的基准连通性曲线与韧性曲线如图9所示.

图9 9度烈度下路网的连通性和韧性曲线
9度烈度下,自0时刻开始,路网的连通性逐渐恢复.t=13 d时,路网的连通性约为0.954,超过了路网连通性期望水平(本文取1)的95%,因此取tf=13 d为路网恢复至期望水平的时刻.路网的韧性也逐渐提高,最终韧性水平为0.885.
3.3 路段韧性重要度评价
t=0代表地震影响结束的时刻,t=3, 6, 9 d分别位于维修前期、中期和后期3个不同的时间段,本文选择t=0, 3, 6, 9 d共4个时刻评价路段的韧性重要度,具有一定的代表性.同时,仅考虑在9度烈度下有中断概率的路段作为研究对象,不考虑9度烈度下完全连通的路段如路段2、4等.其中,路段5和路段10较为特殊,其在9度烈度下完全中断,且这两条路段属于同一路径,仅考虑其中一条连通并不影响路径的状态变化,因此在重要度评价中将其视为一条路段,即5&10.
3.3.1t时刻不同路段连通下的路网韧性曲线 以t时刻路段i连通作为证据,将概率更新后的路网连通性曲线代入式(1),得到相应路网的韧性曲线如图10所示,这里给出韧性重要度较为显著的、具有代表性的路段31、27、5&10和29的相应结果.
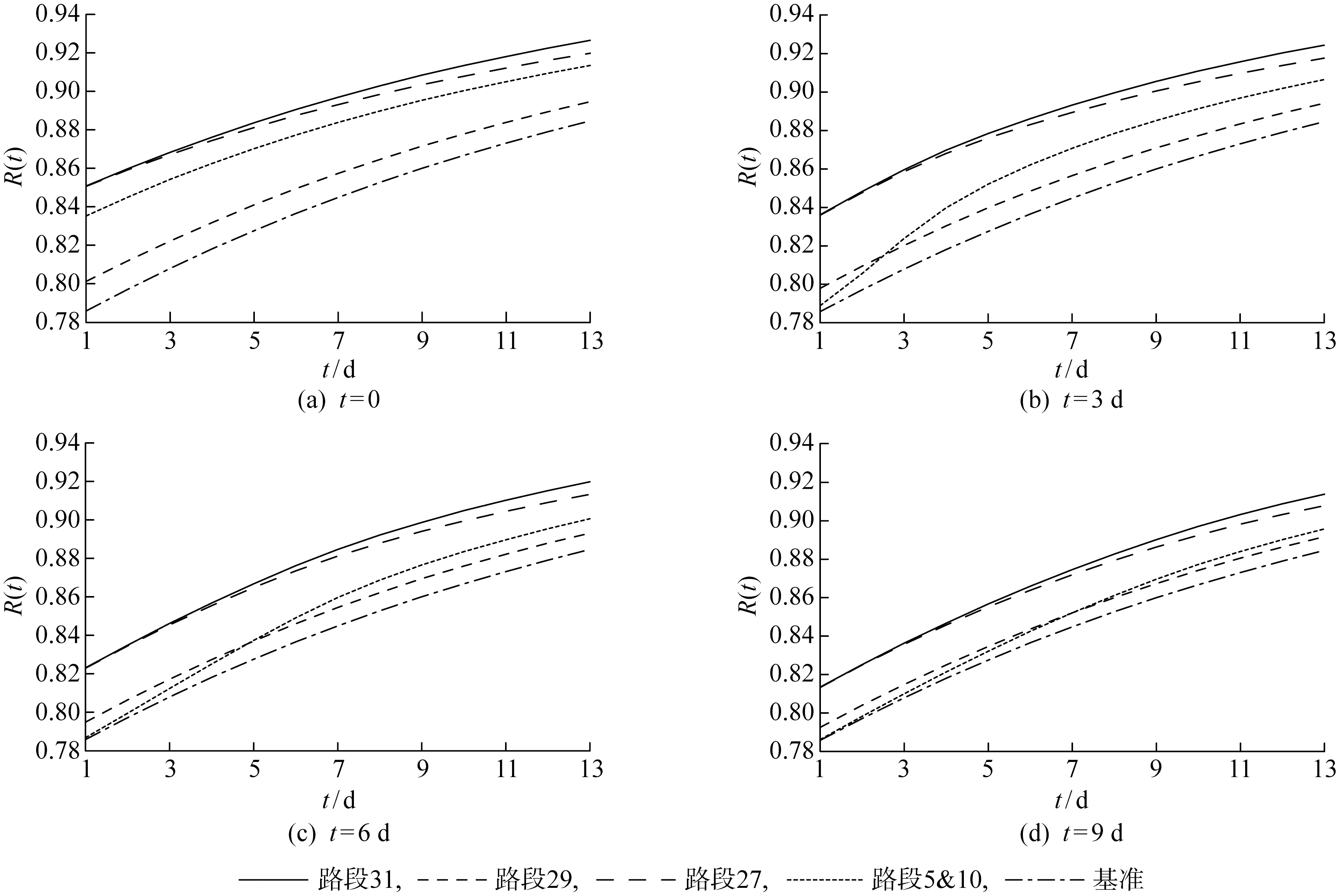
图10 t时刻不同路段连通条件下路网的韧性曲线
从图10可以得到,t时刻不同路段的连通均会提高路网的韧性水平,但提高的程度不同,该提高程度即代表路段韧性重要度.t=0时刻,路段31、27和5&10连通时,路网的韧性水平有显著提高,与基准路网韧性值0.885相比,该3条路段的连通对路网韧性的提高值分别为0.041、0.035和0.028;其余路段对路网韧性的提高程度较为接近,其中路段29的连通对路网韧性的提高值为0.01.t=3, 6, 9 d 时刻,路段31、27的韧性重要度依然较为显著,而路段5&10的重要度逐渐下降.
因此,从路网震前预防策略来看,需要重点关注路段31、27和5&10,提升其抗震鲁棒性能够更高效地提升路网的抗震鲁棒性水平,从而提升路网的抗震韧性.
3.3.2路段在不同时刻连通下的路网韧性曲线 以路段i在不同时刻连通为证据,路网的韧性曲线如图11所示,这里给出路段31、5&10、23和0的相应结果.
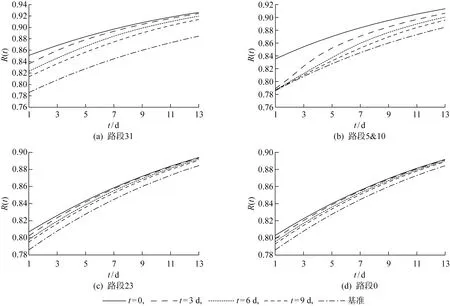
图11 路段i不同时刻连通条件下路网的韧性曲线
从图11可以得到,路段在不同时刻的连通均会提高路网的韧性水平,但提高的程度不同,路段韧性重要度与维修速率成正相关.
不同路段的韧性重要度对t时刻的敏感程度不同.路段31与路段5&10的韧性重要度对t时刻较为敏感,路段23与路段0的韧性重要度对t时刻敏感度较低.以路段5&10为例,t=0时刻其重要度为0.028,t=3 d时刻为0.021,t=6 d时刻为0.015,t=9 d时刻下降到0.011,不同时刻其重要度差距较为显著;而对路段23来说,t=0时刻其重要度为0.009,至t=9 d时刻下降到0.006,差距较小.
因此,从路网震后恢复策略来看,在维修资源有限的条件下,重要度较高且对时间较为敏感的路段的维修优先级应视为最高级,其次为重要度较高但重要度对时间敏感性较低的路段,再次为重要度较低但对时间较为敏感的路段,最后为重要度与时间敏感性均较低的路段.
3.3.3路段韧性重要度总结 根据式(2)计算得到的路段韧性重要度结果如表5和图12所示.

表5 路段韧性重要度结果

图12 各时刻路段韧性重要度
3.3.1和3.3.2节分别从横向(t时刻不同路段)与纵向(路段不同时刻)对比了路网抗震韧性曲线的变化,图12总结了路段韧性重要度的横向与纵向比较结果.从图12可以得到,路段的重要度与重要度对时间的敏感性是路网抗震韧性水平提高程度的两个重要因素.重要度较高且对时间较为敏感的路段连通的时刻越早,路网韧性水平提高越显著;路段31、27和5&10的连通能够显著提高路网的韧性水平,而路段7、30和39的连通对于路网韧性水平的提高程度较小.
路段韧性重要度评价的结果可以为路网震前预防和震后恢复策略的制定提供参考.对震前预防策略来说,需要重点关注t=0时刻重要度较高的路段,如31、27和5&10等,提高路段抗震鲁棒性,从韧性理论中的鲁棒性部分提高路网韧性水平;对震后恢复策略来说,需要合理分配维修资源,优先修复重要度较高且对时间较为敏感的路段,提高路段震后恢复性,从韧性理论中的恢复性部分提高路网韧性水平.
4 结论
已有研究多根据瞬时的构件/路段状态变化导致的系统韧性变化来识别重要构件/路段,同时较少关注除初始时刻t=0外的时刻,基本思路沿袭了可靠性、脆弱性的构件/路段重要度识别,忽略了恢复过程在构件/路段重要度识别中的作用.因此,以路网韧性的增加值RAW为评价指标,提出了一种基于路网抗震韧性的路段重要度评价方法.以9度烈度下青岛市市南区局部路网的路段韧性重要度评价为例,结果表明:
(1) 本文提出的路段重要度指标是对已有路段韧性重要度指标的一种改进,考虑了路段的恢复过程以及对全过程路网韧性(即韧性曲线的变化)的影响.
(2) 同一时刻不同路段的连通均会提高路网的韧性水平,但提高的程度不同;同一路段在不同时刻的连通均会提高路网的韧性水平,但提高的程度不同,路段恢复至连通状态的时刻越早,路网的韧性水平越高.
(3) 不同路段的韧性重要度对t时刻的敏感程度不同.因此,路网韧性策略需要重点关注重要度较高且对时间较为敏感的路段.
(4) 提出的基于路网抗震韧性的路段重要度评价方法实现了从路网韧性到路段重要度的一种整体与局部的联系,从宏观和微观两个视角为路网抗震韧性水平的提高提供参考.
本文提出的路段抗震韧性重要度评价方法能够指导路网震前预防和震后恢复策略制定,从而改善路网韧性,提升抗震减灾水平,但也存在一定的不足之处,后续可以在以下方面继续开展研究工作:
(1) 本文仅考虑了路网抗震性能中最基本的连通性时变曲线作为抗震韧性评价的指标.实际上,运输能力、行程时间可靠性等也属于抗震性能的范围,综合考虑多种抗震性能能够丰富路网抗震韧性评价.因此,后续研究可探索基于多指标的路网抗震韧性评价.
(2) 在维修前期对重要路段进行抢修是提升路网抗震韧性水平最高效的方式,但也对维修资源、成本提出了更高的要求.后续研究可结合不同路段在不同时刻的韧性重要度评价结果与维修资源、成本,探索兼顾成本与效率的震后路网修复策略.
(3) 本文所构建的模型中,假定地震对道路交通系统的影响结束后立刻进行道路抢修工作,忽略了实际情况中的一些延滞时间;同时,假定路段的维修速率都是相同的.实际情况中,维修速率还与路段受损情况、维修资源等相关.后续研究中可基于实际数据,在路段时变特征的表达上对维修速率及状态迁移矩阵进一步改进.

