液体冷却并联通道热沉中的流量分配特性
辛鹏飞, 苗建印, 匡以武, 张红星, 王 文
(1. 上海交通大学 机械与动力工程学院,上海 200240; 2. 北京空间飞行器总体设计部 空间热控技术北京市重点实验室,北京 100086)
随着电子产品集成度和功率的不断提高,电子器件的散热压力也逐渐增大,散热需求达到了 1 000 W/cm2量级[1-2],泵驱两相系统结合微通道换热技术可以获得较高冷却能力,在航空航天、制冷空调、通信、燃料电池等领域为保证电子器件的正常运行都有着广泛的应用和发展前景[3].泵驱两相流在运行过程中存在压力和流量失稳导致的运行可靠性问题,主要分为静态不稳定以及动态不稳定两种类型[4].流量漂移(Ledinegg不稳定)是静态不稳定中经常出现的情况,它是一种系统层面的不稳定性[5].对于单个通道来说,负斜率区域导致在一定压降范围内,压降与流量之间不再是一一对应的关系.对于并联管道来说,由于进出口压降保持一致,因而在流量漂移区间内可能存在多种不同的流量组合.流量的变化使得部分管道的出口为过冷或者过热,从而影响换热器的性能.
在针对多个分散的热控单元进行液体冷却时,多个散热器的并联运行不可避免,散热器间流量的相互影响会导致其换热能力产生一定波动特征.Akagawa等[6]观察了并联蒸汽发生器管道中的流量漂移现象,进行了理论分析并提出了稳定性的判定标准.Minzer等[7-8]研究了太阳能直接蒸汽发生器并联管道中流量分配,理论分析了两并联管道中的流量分布及稳定区域.张炳雷等[9]在低高宽比微通道实验中观察到了流量漂移不稳定现象的存在,发现流量漂移易发生在大流量和低进口温度下.Oevelen等[10-11]利用广义特征值的方法分析大量并行微通道下的流量分配,并考虑了侧壁面导热对流量分配的影响.
在自然循环系统中,也存在多换热器之间流量分配问题.杨瑞昌等[12]建模分析了自然循环压水堆一回路系统内并联换热管内正流和倒流的流量.郝建立等[13]通过分析自然循环蒸汽发生器一回路倒流现象,发现工作于负斜率区域是流量漂移的原因.彭传新等[14]对并联通道两相自然循环系统中流量漂移导致的流动失稳进行实验研究.
文献中针对多并联系统中的稳定性分析采用的方法主要包括线性变换和拉普拉斯变换[6,8,15]、广义特征值解法[10]、矩阵分析[16]等.
现有文献中研究对象多为动力系统和供暖系统的并联管道的流量漂移现象,而对于小型泵驱冷却系统多个并联换热器件的研究相对较少.与并联管道所不同的是,并联热沉间由于流动换热结构、传热所导致的密度和流型变化等原因使得影响流量分配因素更多,出现的特征也有所不同.此外,绝大多数研究的工质以水为对象,在泵驱两相液冷回路中还常采用氨和有机低沸点流体作为工质,其物性与水也有所不同.
本文针对泵驱两相冷却系统的并联多蒸发器进行建模,采用氨作为冷却工质,研究了在较高热流密度下影响单个蒸发器流动特征曲线的因素,并在此基础上研究了相关因素对多蒸发器系统流量分配的影响规律,分析了流量变化对于蒸发器温度分布的影响.
1 理论模型及求解过程
1.1 建立模型
多蒸发器两相泵驱系统如图1所示.图中:Lin表示蒸发器进口连接管道长度;Lout表示蒸发器出口连接管道长度.换热器尺寸参照文献[17]中蒸发器实验模型.为简化计算,对多蒸发器系统进行以下假设:① 蒸发器结构相同;② 蒸发器内部各微通道间流量均匀分配;③ 外部管道内壁光滑;④ 忽略蒸发过程中饱和压力变化对物性参数的影响;⑤ 忽略换热器与外界环境之间的漏热.
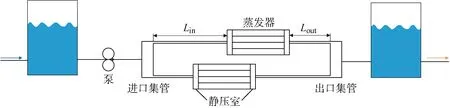
图1 多蒸发器热沉并联模型
本文计算中将单个蒸发器简化成一个单通道换热单元,在此基础上考虑工质在蒸发器内的各个局部压降,包括从管道进出蒸发器静压室、静压室的截面变化以及静压室进出通道等过程中引起的局部阻力.计算中边界条件设置为出口压力保持恒定,每个工况下进口流量恒定,同时,多蒸发器连接在同一集箱上,进出口压差相同.
对于水平方向布置的蒸发器,其一维动量方程为
(1)
式中:G为蒸发器的质量流速;u为通道内流速;z为计算点到通道入口的距离;p为压力;fw为壁面摩擦系数;t为时间.
对于并行蒸发器,蒸发器间的总流量保持不变,满足:
(2)
式中:W为质量流量;N为并行蒸发器的数目.
根据假设,将动量方程沿通道长度进行积分,得到蒸发器的集总参数模型:
pout=pin-pout-Fi(Wi)
(3)
式中:L为蒸发器的等效长度;A为等效截面积;Δpa、Δpf、Δpc、Δpe分别为蒸发器内的加速压降、摩擦压降[18]、突缩压降[19]、突扩压降[20];pin、pout为通道进口、出口压力;Fi(Wi)为蒸发器中各部分压降之和.
对于单相区域,其摩擦压降可表示为
(4)
Po=24(1-1.355 3β+1.946 7β2-
1.701 2β3+0.956 4β4-0.253 7β5)
(5)
式中:pf,sp为单相区摩擦压降;Po为泊肃叶数;μ为运动黏度;ρ为流体密度;ν为比体积;Dh为水力直径;β为通道短边与长边的比值.
两相区域压降摩擦压降表示为
(6)
(7)
(8)
式中:pf,tp为两相区摩擦压降;C为Chisholm因子,在层流状态下为5;x为干度;l表示液相;g表示气相.
蒸发器中突缩压降Δpc、突扩压降Δpe分别表示为
(9)
(10)
式中:γ表示测试通道截面积与集箱截面积的比值;Cc为收缩系数;Ke为膨胀系数;xe,out为蒸发器出口干度;G1为突缩前质量流率;G2为突缩后质量流率.
同时,考虑到蒸发器通道以及壁面在热流下温度变化,将流体和蒸发器壁面沿流动方向分为若干个节点,如图2所示,考虑节点间的导热以及与流体节点间的对流换热.图中:Tf为流体温度;Tw为壁面温度;i为蒸发器中通道的编号.
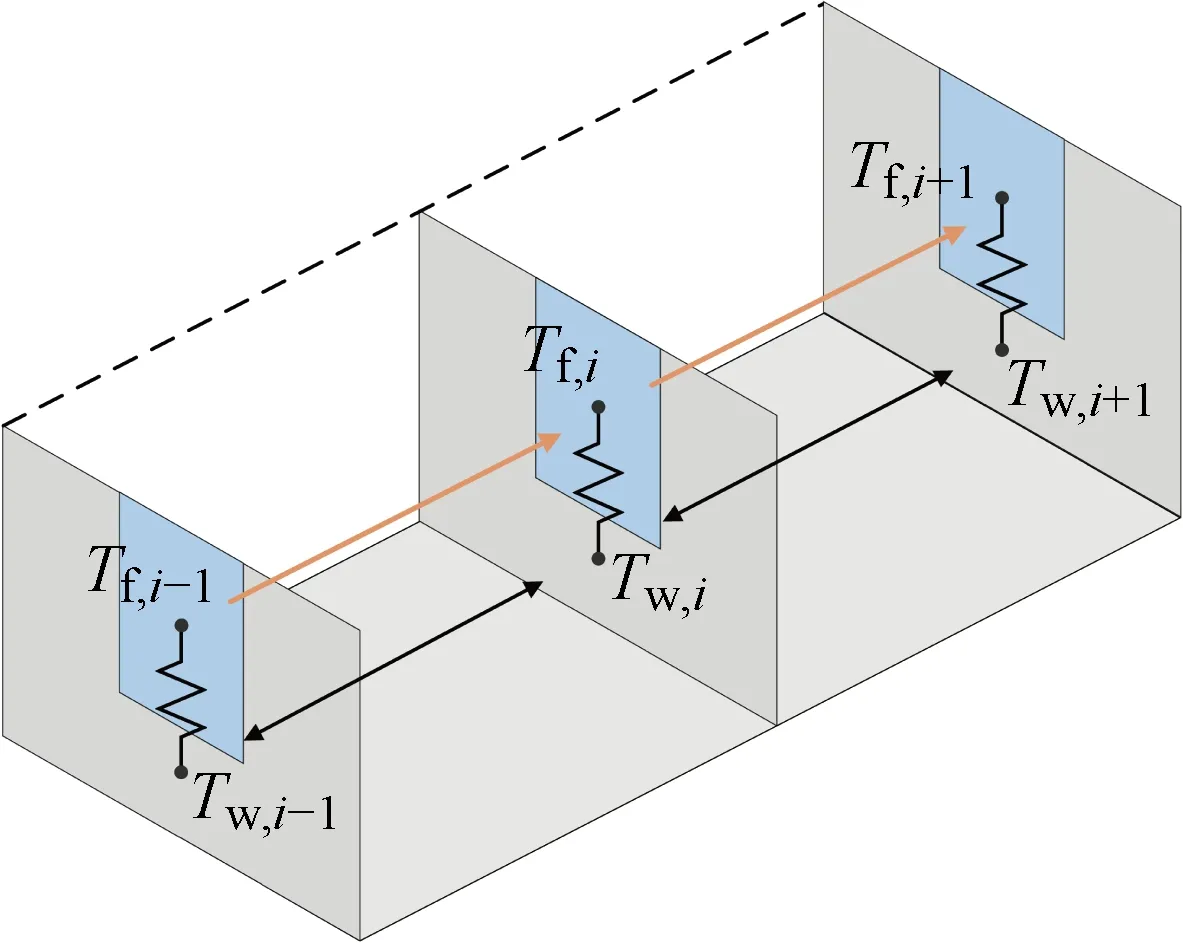
图2 蒸发器节点换热示意图
壁面导热能量方程为
(11)
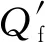
忽略黏性耗散以及流体间的扩散项,流体侧的能量方程为
(12)
式中:Hf为流体焓值.
由于两相区的存在,将流体的温度与焓值的关系用分段函数来表示[11]:
(13)
式中:Tsat为饱和温度;cl为液体比热容;cg为气体比热容;Hl为饱和液体焓值;Hg为饱和气体焓值.
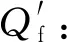
(14)
式中:η0为肋系数,文中取99.12%;hch为蒸发器内的微通道高度;h为对流换热系数,采用Bertsch等[21]提出的关联式,其表达式为
h=hNBS+hconv,tpF
(15)
hNB为核态沸腾项;hconv, tp为对流项;S为核沸腾项的抑制因子;F为对流项因子.
对于壁面的能量方程,考虑到热量在微通道壁面中向前后两个方向的传递,对扩散项采用中心差分的格式;对于流体能量方程中的对流项,采用一阶迎风格式[22].
氨是一种自然制冷剂,在微通道中的流动换热研究较少.氨具有仅次于水的汽化潜热,工作压力较高,表面张力较小,全球变暖潜能值(GWP)和消耗臭氧潜能值(ODP)为0[23],在热泵制冷[24]、航空航天[25]、环路热管[26]等领域有着较多的应用,本文将采用液氨作为冷却工质,选取的饱和温度为25 ℃.
蒸发器的材料为铜,表面镀镍,结构参数为:wch=0.4 mm;hch=0.6 mm;L=10.8 mm;wf=0.3 mm;底层厚度wt=1 mm.采用局部加热的形式,加热区域长度为6 mm,位于蒸发器底部中央.
1.2 稳定性分析
根据李雅普诺夫稳定性的理论,省略非线性方程中的高次项,利用近似一次线性系统的稳定性准则来评价其稳定性[27].并联热沉进出口压力相同,可表示为
(16)
代入式(3)可得:
(17)
令Wi=Wi0+wi,其中Wi0为稳态时i蒸发器内的流量,wi为稳态时受到的扰动量.令W=[W1W2…WN]T, 则初始状态点为W0=[W10W20…WN0]T,在W0处做泰勒展开,
(18)
其中,特征矩阵B为

(19)
令ΔW=W-W0=Keλt,代入式(11)可得:
(20)
式中:λ为特征根;m为等效惯性系数(L/A);K为系数矩阵.
当系统特征矩阵B的特征根λ全为负值时,系统是稳定的;当至少有一个特征根λ>0时,系统是不稳定;当仅存在零实部的特征根,则不能判断原系统的稳定性.
1.3 计算流程及模型验证
图3表示了计算的流程图.图中:Tw,new为迭代后壁面温度;Tf,new为迭代后流体温度;Hf,new为迭代后流体焓值;RH为流体焓值迭代设定残差;RT为温度迭代设定残差.对于单个蒸发器,沿流动方向将蒸发器分为若干个节点,先通过Gauss-Seidel方法迭代计算蒸发器的壁面和流体的温度分布,再根据每个控制体内流体的温度求解对应压降,结合蒸发器的局部压降得到系统的流动特征曲线.并根据单个蒸发器的流动特征曲线,得到系统的特征曲线以及蒸发器间的流量分配情况.

图3 计算逻辑图
在进口温度为5 ℃时,对蒸发器的壁面温度进行网格无关性检验,如图4所示.在收敛标准一致的情况下,随着划分网格数目Nc的增加,其温度分布逐渐趋于一致.为保证计算精度以及减小计算量,沿流动方向将划分216个一维网格.
图4 网格无关性检验
将模型计算结果与Miglani等[28]以水为工质、通道尺寸为1 mm×1 mm×55 mm的微通道流量分配实验数据对比,总体积流量Q=9.3 mL/min,入口温度Tin=88.5 ℃,饱和温度Tsat=100.8 ℃,如图5所示.图中:Wtot为总流量;Wi/Wtot为流量比;PT为总加热功率.可以发现,模型计算结果与实验模拟结果比较吻合,最大偏差为3.2%.综上所述,此模型满足计算要求.

图5 模型验证
2 结果分析
2.1 影响蒸发器系统流动特征曲线的因素
与常规通道相似,进口过冷度ΔTin、热流密度Q″、饱和温度Tsat以及通道水力直径Dh都会影响蒸发器的流动特征曲线,如图6所示.图中:Δp为蒸发器压降;灰色虚线表示负斜率区域的消失的边界.图6(a)中,随着进口过冷度的减少,负斜率区域倾斜程度逐渐降低,负斜率区域对应的长度先增加后减小,进口过冷度增加到一定数值后,负斜率区域消失.加热功率的影响如图6(b)所示,随着加热功率的增大,负斜率区域从无到有,倾斜程度逐渐增大,且对应的负斜率区间长度逐渐增大.在进口过冷度一定时,饱和温度的影响如图6(c)所示,饱和温度的增加会降低工质间的密度差,从而降低通道内的孔隙率,使得两相摩擦压降降低[29],饱和温度的提高会降低负斜率区域的长度和倾斜程度,提高稳定性.通道尺寸的影响如图6(d)所示,微通道水力直径Dh的减小会增加整体的压降,却减小了负斜率区间的倾斜程度,原因在于增加了通道进口的局部压降,类似于节流的效果,可以提高系统的稳定性.可以发现,虚线所代表的负斜率消失对应的质量流速随着进口过冷度的减小、加热功率的增大、饱和温度的增大以及微通道水力直径减小而增大,而饱和温度的增大对应着汽化潜热的降低,这与Kuang 等[30]得到的理论表达式变化趋势相同.

图6 热力参数和通道尺寸对蒸发器流动特征曲线的影响
在相同的过冷度15 ℃和加热功率下,水和氨的流动特征曲线如图7所示,可以看出,以水为工质的整体压降大于以氨为工质,且水的负斜率区域的范围和倾斜程度远大于氨.由于水的液气密度比为 1 600,远大于氨的77,导致在两相出现区域水的压降比较大.在相同的过冷度下,由于氨的比热容较大,使得氨的沸腾起始点小于水.但在纯液体工况下,由于相同质量流速下,氨的流速较大,使得其压降大于水.

图7 水和氨的流动特征曲线
蒸发器进出口连接管长度对系统流动特征也会产生影响,如图8所示.当进口管道长度增加时,负斜率对应的范围以及倾斜程度明显减少,主要因为进口单相段压降是流量的单调函数,能够提高系统的稳定性;当出口管道长度增加时,负斜率对应的区间以及倾斜程度会明显增加,原因是出口管道多为两相混合物,其压降与流量之间的函数关系是非线性的,从而使得系统的稳定性降低.图9表示在连接管道总长为220 mm时,进口管道内的压降Δpin、出口管道内的压降Δpout与总压降Δptot的比值.当出口长度较长时,管道内的压降会大于蒸发器内部的压降,而出口管道流动特性曲线中存在的负斜率区域会增加系统的不稳定性;进口长度较长时,进口管道压降较大的占比会提高系统的稳定性.当进口管道长度增加到一定数值后,可以抵消蒸发器产生的负斜率区间,但会增加系统整体的压降和占用的空间.因此,对于特定的多热源冷却系统,合理的安排蒸发器的位置有助于提高系统的稳定性.

图8 进出口管道长度对流动特征曲线的影响
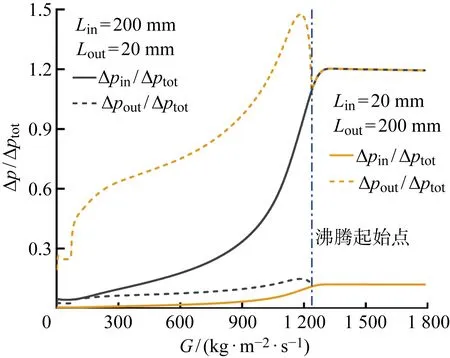
图9 进出口连接管道内压降与蒸发器内压降比值
2.2 多蒸发器间的流量分配特性
由于蒸发器流动特性曲线中负斜率区域的存在,在满足质量守恒与动量守恒的前提下,蒸发器内部的流量分配有着多种的可能性.当进口过冷度ΔTin=20 ℃,总质量流速Gtot=1 500 kg/(m2·s)时,蒸发器中的流量分配存在3种情况,图10中两个换热单元的流量压降曲线相交于各自的负斜率区域,其对应的质量流速和始终为 1 500 kg/(m2·s),两条流动特征曲线的交点即为可能的流量分布情况.图中:Δp1为蒸发器1压降;Δp2为蒸发器2压降;x1为蒸发器1出口干度.当两个蒸发器完全相同时,其流量组合为(1 101/399) kg/(m2·s)或(750/750) kg/(m2·s).将工况点代入式(20)计算特征矩阵的特征根,工况点1、3特征根实部为负值,相对稳态流量变化量ΔW在扰动后逐渐降低,是稳定工作点;工况点2为正值,ΔW在扰动后逐渐增大,为不稳定工作点.图中:Wa表示沸腾起始的质量流速;Wb表示负斜率区域消失的质量流速.从而将流动特征曲线分为3个区域,III 区位于单相液区,II 区以及 I 区大部分位于两相区,单相气区在整体流量变化中占据的范围较小.

图10 两并联热沉间的流量漂移
流量漂移的存在使得部分蒸发器得到更多的流量,从而出口为单相状态;部分蒸发器得到较少的流量,出口流体为高干度甚至过热状态.如上图初始状态两个蒸发器流体的出口干度均为0.02,当发生流量漂移后,蒸发器流体的出口干度变为0.12或0.两相区流体的干度对流体对流换热系数有着比较大的影响,因此流量的变化会对蒸发器整体温度分布有着比较大的影响.

图11 流量漂移前后蒸发器壁面温度、流体温度以及单位长度对流换热量的变化
通过对上述进行分析可以发现,在部分区域加热时,发生流量漂移之后对于蒸发器整体温度分布来说,不一定是不利的.如上述情况下,流量漂移增加了一个蒸发器整体换热系数,使其壁面温度降低,而另一个蒸发器壁面温度不会发生明显的变化.
图12为大范围质量流速下两个蒸发器由于流量漂移而出现的系统压降和流量分配特征,进口过冷度为20 ℃、加热功率为500 W/cm2,其中红色虚线表示不稳定状态,蓝色实线表示稳定状态,并表示出上文讨论的工况点.可以发现,在此参数下不稳定的工况点主要出现在两个蒸发器都运行在负斜率区域时,这是由于蒸发器在此参数下的流动特征曲线负斜率区域较为平缓.将图10中的沸腾起始流量Wa和负斜率区域消失流量Wb表示在图12中,假设蒸发器2中的流量始终高于蒸发器1,其流量分布为带有灰色阴影的曲线.在沸腾起始流量Wa之前,蒸发器内部呈现均匀分配状态;流量继续降低导致流量分配不均的情况出现,蒸发器2在 III 区随总流量减小而增大到极值W2,max,蒸发器1在 II 区流量降低直到Wb.总流量继续降低,蒸发器2在 II 区流量从极值W2, max降低到Wa,蒸发器1在 I 区流量降低到极小值W1,min.随后,总流量的降低使得蒸发器1的流量增加、蒸发器2的流量减低,最后都达到负斜率消失点Wb,此后两蒸发器间保持均匀分配的状态.

图12 两并联热沉的流量分配
为了评价蒸发器间的流量分配,引入无量纲流量βi[32]和流量分配不均匀系数φ:
(21)
(22)
式中:n为工况点数目;βavg为n个工况点的平均无量纲流量.


图13 不同加热功率下的两蒸发器流量漂移
当进口过冷度逐渐降低时,所有工况的不均匀系数φ随之降低,如图14所示.因为随着进口过冷度的降低,蒸发器流动特性曲线中的负斜率区域斜率减小,从而降低了工况的不均匀程度.当进口过冷度达到15 ℃后,不稳定区间只会出现在均匀分配的区域,不稳定工况点的不均匀系数变为0.不均匀分配程度随过冷度减小逐渐降低,直至完全消失.

图14 不同过冷度下两蒸发器的不均匀系数和不稳定区间占比
由于进出口的管道长度会影响蒸发器的流动特征曲线,所以蒸发器的布置对系统的流量分布有着比较大的影响.图15表示在进口过冷度为20 ℃、加热功率为500 W/cm2时,当总长度保持不变,采用流量分配不均匀系数φ表示蒸发器布置位置对系统流量分布的影响.当蒸发器之间的距离发生变化时,其流量分配情况也存在一定的差异.定义无量纲长度di=d/Ltot,表示蒸发器间距在总长度所占的比例.可以发现,在总长度为220 mm时,随着di增大,所有工况点的不均匀系数呈现逐渐增大的趋势,这是由于随着蒸发器之间距离的增大,其流动特征曲线的差异逐渐增大,导致蒸发器的运行状态更加偏离均分的情况,进口管道长的蒸发器内,会得到更多的流量.稳定工况点除di为0.636外,其余均呈现上升的趋势,而不均匀系数的下降是因为不均匀分配工况中稳定点所占比例减小导致的.此外,随着蒸发器之间距离的增大,其最大流量比也会增加,在这些工况点发生流量漂移后的危害也会增大.

图15 不均匀系数和最大流量比与两蒸发器间距离的关系
3 结论
本文针对并联微通道热沉系统进行建模,研究在部分区域加热情况下蒸发器热沉系统中的流量分配问题,并分析了不同参数对单个蒸发器以及系统的影响情况.为了更好地表示流量分配对蒸发器系统的影响,对蒸发器的温度分布进行了计算.主要结论如下:
蒸发器系统中的静态不稳定性与其流动特征曲线的负斜率区域相关.进口过冷度的增加、加热功率增加以及饱和温度的降低都会增加流动特征曲线的负斜率倾斜程度,引起系统的不稳定;通道尺寸的降低可以增加进口压降,从而降低负斜率区域倾斜程度,但会增加系统整体压降.
蒸发器的结构参数对不稳定性也会有较大的影响.在总长度保持一定时,增加蒸发器进口连接管道所占比例能够提高系统的稳定性,甚至可以消除负斜率区域;增加出口连接管道所占比例会加剧系统的不稳定性.合理安排蒸发器的位置有利于提高系统的稳定性.
当蒸发器系统运行在不稳定区间时,受到扰动便会产生流量漂移,从而改变蒸发器间的流量分配情况.通过表示出不同流量下蒸发器温度的分布情况,可以发现,在部分加热的条件下,产生流量漂移不一定会恶化系统的对流换热.流量降低使得部分两相区出现在加热区域内,换热系数的增大降低了蒸发器壁面的最高温度.而得到更多流量的蒸发器由于全部是单相换热,其平均温度会大于初始状态.
两个蒸发器加热功率存在差异时,低加热功率的蒸发器会得到更多的流量,随着加热功率差异的增大,其不均匀程度也会增加;进口过冷度的减小会降低系统整体的不均匀分配程度,由于两相区长度的增加,其不稳定区间占比先会有所上升,最后负斜率区域消失,不稳定区间也消失;不同的进出口管道长度配置会影响系统流量的分配倾向,进口长度占比大的通道会得到更多的流量,随着蒸发器间的无量纲间距增大,其不均匀程度也会增加,发生流量漂移后的危害也会增加.

