加工时间为区间数的两阶段流水生产鲁棒调度

张先超，周 泓

1.东南大学 信息科学与工程学院，南京 210096

2.北京航空航天大学 经济管理学院，北京 100191

生产调度是将有限的资源，如设备、场地、人员等，按时间分配给任务，使得一个或几个目标值达到最优。由此可见，生产调度涉及到任务、资源和任务在资源上的处理时间等众多因素。然而，实际生产过程中的很多因素是不确定的，经常导致无法按照既定的初始调度方案实施生产，在生产过程中需要对初始调度方案进行一定的调整，这对生产过程和生产结果都会产生一定的影响。在这种情况下，为了顺利完成生产，确保生产结果，要求初始调度方案在一定限度的不确定因素扰动下，小幅调整即可实施，并能实现满意的结果。将初始调度具有的这样的性质称为鲁棒性，具有鲁棒性的初始调度方案称为鲁棒性初始调度方案。可以使用在不确定因素扰动下，实际调度目标与能够达到的最优调度目标的差距作为调度鲁棒性的指标，用以度量初始调度方案的鲁棒性[1]。

在离散制造业中，流水车间（flow shop）是一种典型的作业模式，在生产制造的整个过程或关键部分环节被广泛运用。两台机器串行构成的两阶段流水线是最为简单的流水车间结构，其调度问题的研究，在理论上是其他更为复杂的流水车间调度问题研究的基础，在实际生产中也有着广泛的应用，例如，汽车的某些冲压件需要依次经过整形和冲孔两道工序。

加工时间不确定是制造过程中一种常见的影响调度方案实施的不确定因素，以往很多学者将不确定的加工时间作为随机变量，求解期望调度目标最优的调度方案，称这样的调度问题为随机调度，可以使用随机优化等多种方法予以解决[2-3]。然而，在很多情况下，加工时间未必服从某一确切的概率分布函数，即便如此，也难以获得准确的概率分布，此外，非常满意的随机调度方案在一次具体的生产过程中也可能导致较差的生产结果。因此，在加工时间不确定的环境下，随机调度具有很大的局限性。相比随机调度，鲁棒调度不要求加工时间的准确的分布函数，而且，求取的调度方案在任何可能的加工时间情景下都能获得比较满意的生产效果。

近年来，对于加工时间不确定的鲁棒调度问题，已经有了一定的研究。文献[4]给出了流水车间调度算法的鲁棒性。文献[5]研究了加工时间是离散情景，分布式流水生产鲁棒调度问题的局部搜索算法。文献[6]研究了加工时间不确定的job-shop鲁棒调度问题，也是将加工时间描述为离散情景，运用邻域搜索，结合模拟退火和邻域搜索求解。加工时间为离散情景在实际生产中并不常见，用区间数来表征实际生产中的加工时间更具有适用性。Liao等[7]研究了加工时间为区间数的置换流水车间Min-Max准则鲁棒调度问题，并运用遗传算法求解该问题。Levorato 等[8]研究了加工时间是区间分布，以工期为调度目标的鲁棒调度问题，建立混合整数规划模型，使用列和约束生成算法求解。Wu等[9]也是针对以工期为目标的两阶段流水车间，研究了加工时间依赖具体情境的Min-Max鲁棒调度问题。相比工期，总完工时间在实际生产中有着更广泛的意义，例如，总完工时间与库存密切相关，减小总完工时间可以降低库存，提高资金周转率。进一步来看，使用总完工时间作为调度目标，对于生产以外的其他领域也同样具有很好的适用价值。文献[10]研究了针对云资源，以总完工时间为目标的调度问题。Sun等[11]研究了以总完工时间及其偏差的和为目标的流水车间鲁棒调度问题，但其加工时间表征为离散情景。

流水车间鲁棒调度问题的求解往往具有很高的复杂性，降低计算复杂性也是研究的重点。Cwik等[12]针对加工时间为区间数的，以工期为调度目标的流水车间鲁棒调度问题，通过两次松弛来降低计算复杂度。利用调度解的占优特点（dominance）是降低复杂性的常用手段。在不确定加工时间的环境下，很少存在对于任何加工时间情景都是最优的调度解，但可能会存在任意加工时间情景下，某些调度解都会优于另外的一些调度解，称这样的调度解是占优的。Allahverdi和Sotskov[13]证明了加工时间是随机数或区间数的两台机器流水车间鲁棒调度占优解的充分条件。Matsveichuk和Sotskov等[14]求解了该鲁棒调度问题的占优解集，对于某一特定的加工时间情景，占优解集至少包含这种加工时间情景下的一个最优调度解。Wu等[15]针对以总完工时间为目标的两阶段流水车间调度问题，给出了利用占优条件的分支定界算法，以及CA、GSA 等启发式算法。然而，占优解集在实际应用中有着很大的局限性，需要根据当前的生产情况实时选择调度方案，需要高效率的算法支持，且对实现的调度目标没有准确的预期。

本文研究以总完工时间作为调度目标，加工时间为区间数的两阶段流水生产鲁棒调度问题，使得在所有可能的加工时间情景下，调度目标相对相应的最优调度目标的最大偏差最小，即求解Min-Max准则的鲁棒调度解。

1 问题描述与模型

1.1 鲁棒调度的三元组形式

1.2 鲁棒调度的三元组形式

由此，调度在所有加工时间情景下调度目标相对最优调度目标的最大偏差为：

设调度σR满足：

则调度σR为调度目标最大偏差最小的调度方案，即Min-Max准则的鲁棒调度方案。

1.3 数学模型

为建立问题的数学规划模型，引入变量xjk和，规定如下：

式（4）给出了xjk(j,k=1,2,…,n)与调度σ的一一对应关系。那么，在加工时间情景λ下，调度σ的第j个位置的工件σ(j)在两台机器上的加工时间为：

同理，根据式（5），得到：

根据式（7）和（8），在加工时间情景λ下，调度σ和最优调度σλ中第j个位置的工件σ(j)和σλ(j)的完工时间分别为：

那么，调度σ和σλ的总完工时间为：

根据式（11）和（12），得到：

由此，式（3）转换为以下的整数规划模型：

在模型（14）中，约束（a）使得每个工件在调度σ中位于且仅位于一个位置，约束（b）是调度σ中每个位置有且仅有一个工件，约束（c）是式（6）对的求解，约束（d）表明xtk是0-1变量。

进一步，式（14）改写为：

模型（15）中约束（b）到（e）同模型中约束（a）到（d），求解的τ即为最小最大调度目标偏差。根据模型（15）的解{xtk|t,k=1,2,…,n} 形成的调度方案即为Min-Max准则的鲁棒调度σR。由于区间数加工时间的情景集合Λ是无穷集合，那么，模型（15）具有无穷约束，是半无限规划模型。

2 简化性质与占优性质

根据式（18），对式（13）进行变换，得到：

根据式（19），式（2）给出的区间数加工时间环境下，调度σ的总完工时间最大偏差的求解如式（20）所示：

定理1（简化性质）对于给定的调度σ，使得总完工时间偏差最大的情景一定是工件加工时间取其所在时间区间的极端值。

定理1 将区间数工件时间转化为可列可数加工时间情景，使得模型（20）的约束个数有限化，模型得以简化，便于问题的求解。

设b是B中的任意一个工件，b∈B，那么

设c是C中的任意一个工件，c∈C，容易得到：

根据式（22）、（24）、（26）和（27），得到：

定理2成立。

定理3（占优性质）对于已经给出调度方案的工件集合σs，以及尚未调度的工件i和j，如果满足以下条件：

则存在工件j不是工件集合σs的紧后工件的鲁棒调度方案。

设调度σ={σsiAjB}，对于满足给定条件的任意加工时间情景，都有：

又根据式（30）的给定条件，得到：

根据式（31），易得：

根据式（32）和（33），得到：

显然

那么，根据式（29），得到：

又因为

根据式（35）、（36）和（37），得到：

根据式（32）、（34）、（36）和（38），得到：

定理3成立。

定理2 和定理3 给出了所求调度的占优条件，用以缩小解空间，可以减小分支定界方法搜索的节点数目，从而降低求解难度。

3 分支定界-遗传算法

在加工时间为区间数的环境下，Min-Max准则鲁棒调度解的搜索涉及到调度解和加工时间两个空间。先对于给定的调度解，搜索总完工时间偏差最大的加工时间情景，再从调度解空间中搜索最大偏差最小的调度解，即鲁棒调度解。遗传算法具有很好的全局搜索性，具有广泛的适用性[17-18]。本文将分支定界方法与遗传算法结合起来，设计分支定界-遗传混合算法（branch and bound-genetic algorithm，BB-GA），运用遗传算法搜索给定调度解的总完工时间偏差最大的加工时间情景，再运用分支定界方法从解空间中获得min-max 准则的鲁棒调度解，如图1所示。

图1 BB-GA算法框架Fig.1 Framework of BB-GA

根据定理1，求解给定调度解的总完工时间最大偏差的加工时间向量，只需要搜索各加工时间区间的端点值即可。因此，遗传算法可采用0-1编码，染色体长度等于工件数量与机器台数的乘积。采用这样的方式解码，染色体的各基因位依次对应给定调度解的各加工时间，如果基因位是“0”，则相应的工件加工时间取其区间下限，反之，基因位是“1”，则相应的工件加工时间取其区间的上限，从而，染色体与加工时间向量一一对应，实现了遗传算法的编码与解码。

对于给定的调度解，遗传算法的一条染色体对应一种加工时间情景，那么，可以依据式求取该染色体对应的总完工时间偏差，以此作为适应度函数，进行遗传算法的种群选择。从而，求取给定调度解的总完工时间最大偏差。

分支定界算法采用深度优先策略，按照字典序依次搜索。对于搜索到的新的分支，如果部分序的下界小于已有的上界，或者不满足定理2或定理3，则搜索下一个分支，否则，延长部分序的长度，计算其下界，并判断对于定理2和定理3的满足性。如果沿着一条路径搜索到了最底层，也就是形成了完整的调度解，所有工件都已安排，验证其总完工时间最大偏差是否小于已有的上界，如果小于已有的上界，则替代形成新的上界，并记录该调度解，否则，按照深度优先策略搜索下一路径。依此，直至搜索完全部路径。

用MD表示总完工时间最大偏差的最小值，σ表示字典序的当前序列，σ′表示字典序的下一个序列，σl表示σ中l个工件的部分序，σ(l)是σ中第l个工件，表示σl的总完工时间最大偏差下界，σR是所求解的鲁棒调度。

算法步骤如下：

输入：n个工件在两台机器上的加工时间区间。

输出：总完工时间最大偏差最小值MD，及鲁棒调度σR。

步骤1设定σ={1,2,…},n,l=1,MD为足够大的初始值。

步骤2根据遗传算法（GA）求解,如果≤MD，σl满足定理2 和定理3，且l ＜n，则l=l+1，返回步骤2；否则，如果＞MD，或σl不满足定理2或定理3，转到步骤3。

步骤3如果l=n，转到步骤4；否则，如果σ(l)＜n，则σ=σ′,返回步骤2，如果σ(l)=n,则σ=σ′,l=l-1,返回步骤2。

步骤4如果＜MD,则=MD,σR=σl；如果σ(1)=n,σ(n)=1,算法结束，输出最大偏差的最小值MD和鲁棒调度σR,否则，σ=σ′,返回步骤2。

在图1中，算法的效果由运用遗传算法求解给定调度解的完工时间最大偏差，以及运用分支定界求解完工时间最大偏差最小的调度解两部分决定，由于分支定界算法是确定性算法，能够得到最优解，因此，算法效果主要取决于前者。

4 仿真实验

4.1 实验设计

仿真实验硬件设备为配备Intel®CoreTMi9-11900K @3.5 GHz处理器的台式计算机。

开展两类实验，一是针对给定调度方案，验证遗传算法求解其总完工时间最大偏差的优越性；二是验证求解的初始鲁棒性调度方案的鲁棒性。

4.2 总完工时间最大偏差的实验分析

从每个问题中随机产生10个实例，在每个实例中，对工件按照生成的先后次序进行排序，以按照生成次序排序的调度方案作为给定调度方案。针对每个问题，对各实例分别运用遗传算法、模拟退火算法、禁忌搜索算法求解总完工时间最大偏差，以及随机选取另外一个调度方案，求解其总完工时间偏差，然后求解10个实例总完工时间最大偏差的平均值。这几类算法在智能优化中具有典型性。结果如图2所示。

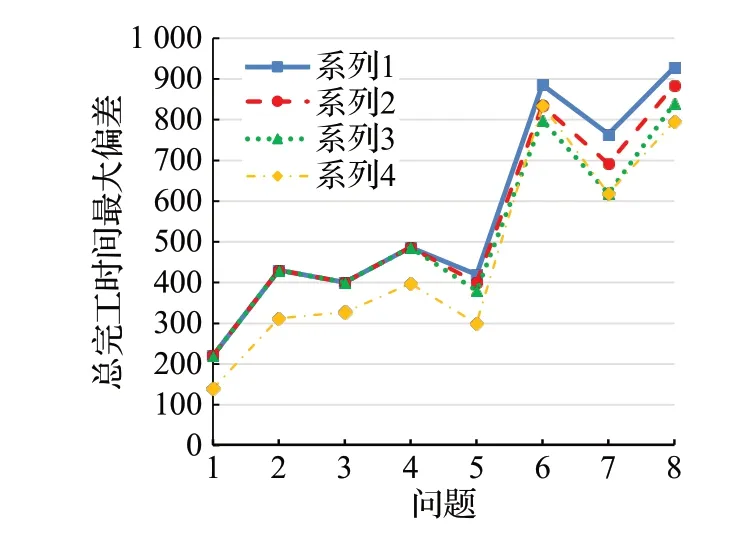
图2 总完工时间偏差最大值仿真结果Fig.2 Maximum deviation of total completion time

从图2 可以看出，对于给定调度方案，遗传算法求解的总完工时间偏差最大值大于其他各类算法，当问题规模增大时，优势更为明显。

4.3 初始调度方案鲁棒性的实验分析

（1）验证指标

从每个问题中随机产生10 个实例，分别记录和计算每个问题的10 个实例中最优期望调度（以期望加工时间作为调度目标求解的调度方案）σE的总完工时间最大偏差与鲁棒调度σR的总完工时间最大偏差的最大比值MaxDev(E/R)、平均比值MeanDev(E/R)和最小比值MinDev(E/R)，鲁棒调度σR的期望总完工时间与最优期望调度σE的期望总完工时间的最大比值MaxTc(R/E)、平均比值MeanTc(R/E)和最小比值MinTc(R/E)。各指标如表2所示。

（2）实验结果

仿真实验结果如表3所示。

在表3 中，第（1）列是问题编号，第（2）列是工件数目，第（3）和（4）列分别是α1和α2的均匀分布区间，第（5）到（10）列分别是表1给出的指标。第（5）到第（10）列的各列中圆括弧标出了各列的最小值，方括弧标出了各列的最大值。

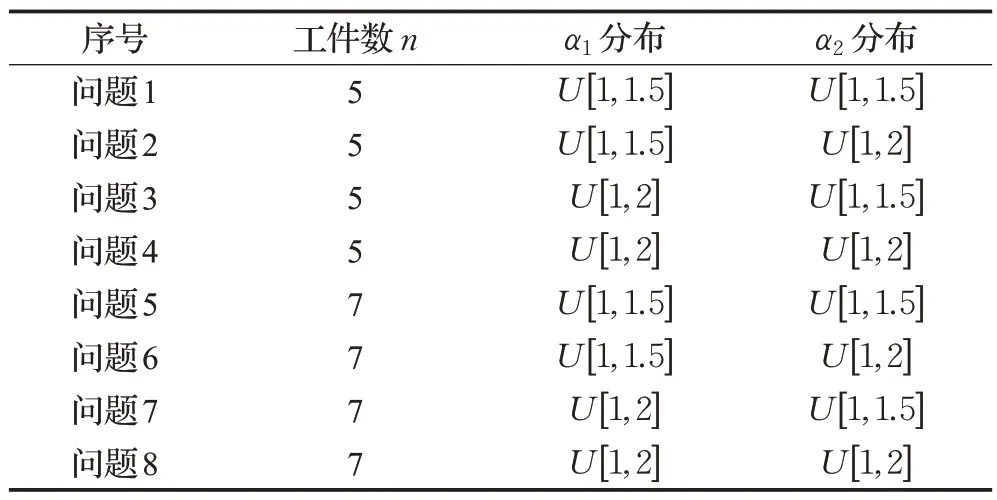
表1 实验问题Table 1 Experimental questions

表2 计算实验比较指标Table 2 Indices of computational experiments

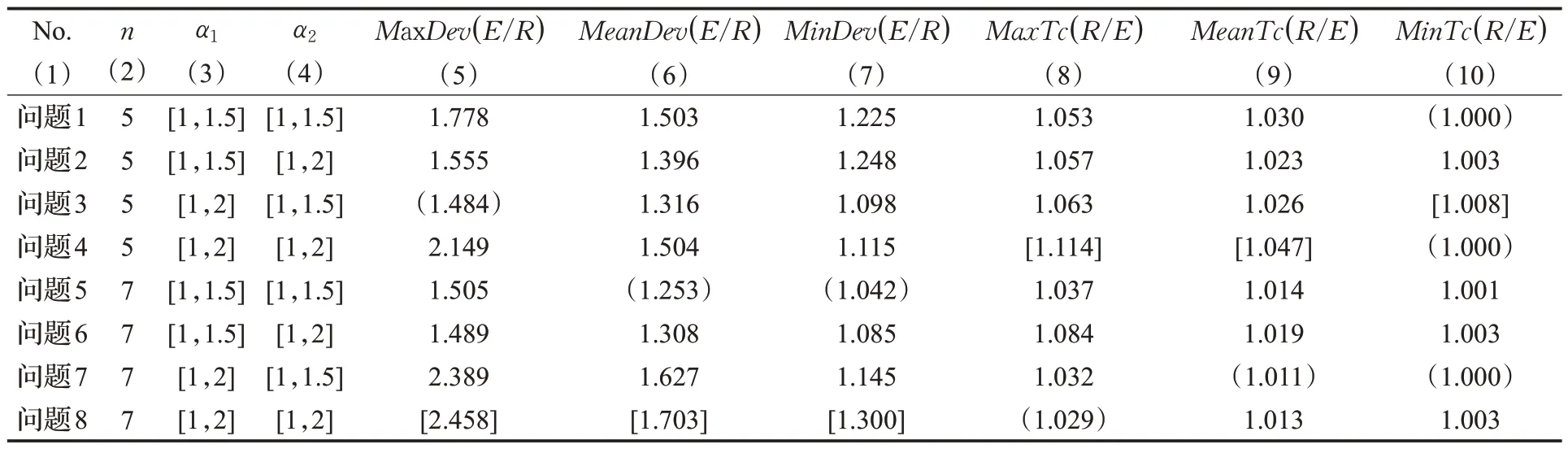
表3 计算实验结果Table 3 Result of computational experiments

（3）实验分析

从表3 可以看出，在各组问题中，最优期望调度的总完工时间最大偏差都明显大于鲁棒调度，各组最大偏差比值的最大值高达2.458，最小值有1.484，各组平均偏差比值的最大值达到1.703，最小值为1.253，各组最小偏差比值的最大值有1.3，最小值也有1.042。从鲁棒调度的期望调度目标与期望调度的目标比值来看，各组中最大比值的最大值只有1.114，平均比值的最大值仅有1.047，最小值为1.011，而各组最小比值的最大值仅为1.008，最小值则为1，也就是说二者有着相同的期望总完工时间。

图3 展示了实验结果，横轴是问题，纵轴是比值，6条折线分别是表1 中的6 个指标。图2 中，对于8 个问题，指标1、2和3明显大于指标4、5和6。而且，指标4、5和6都接近于1。

图3 实验分析Fig.3 Experiment analysis

表3和图3充分表明：

（1）鲁棒调度能够有效克服加工时间的不确定性的扰动，避免生成总完工时间偏差较大的调度方案；

（2）鲁棒调度相比最优期望调度的性能损失很小。

计算实验验证了本文的鲁棒调度方法能够生成总完工时间偏差较小，而性能损失较小的初始鲁棒调度方案，能够有效解决加工时间是区间数，以总完工时间为调度目标的两阶段流水车间调度问题。

5 结语

本文研究了以总完工时间作为调度目标，加工时间为区间数的两阶段流水车间鲁棒调度问题，求解所有加工时间情景下，使得能够获得最优调度目标最大偏差最小的鲁棒性初始调度方案，即Min-Max 准则的鲁棒调度。以总完工时间为调度目标的调度问题作为研究对象，更符合实际生产需要。建立了该类鲁棒调度问题的半无限规划模型，证明了问题的一个简化定理和两个占优定理，简化定理将半无限规划模型转化为等价的有限约束的模型，占优定理用以缩小解空间。建模与定理证明的理论价值显著，对于类似问题的研究具有很好的借鉴意义。设计了求解的分支定界-遗传算法，使用遗传算法获取给定调度解的完工时间最大偏差，分支定界算法搜索调度解，利用了遗传算法的全局搜索性和分支定界的全局最优性，混合算法效果良好。本文的研究对于生产以外的其他领域，还可以推广应用于供应链、信息网络等其他领域。