水资源优化配置在枋洋水利枢纽的应用

赵玉娇，苏煜杭，杨 晔，李书明

（1.国电南京自动化股份有限公司,江苏 南京 210061；2.厦门水务原水投资运营有限公司,福建 厦门 361000）

0 引言

时空分布不均是我国水资源的显著特征,因此造成的水资源不合理使用以及水资源污染、浪费等情况加剧了各地区水资源供需矛盾。水资源统一调配是解决供需矛盾的主要方法,但水资源的统一调配是一个复杂的、系统性的问题,需要考虑社会、经济和生态等方面。所以,水资源的优化调配是一个多目标优化问题。

自从二十世纪五十年代起,许多专家学者参与到了水资源体系的优化调整和研究中。目前,调度模型的常用求解方法有动态规划方法、大系统分解协调方法、模拟方法、人工神经网络法和遗传算法等[1]。在水资源优化调度领域比较成熟的算法是遗传算法[2]和人工神经网络算法[3]。蚁群算法[4]、模拟退火算法[5]、粒子群算法等新型智能算法也开始得到应用。但这些算法通常存在收敛速度慢,容易陷入局部最优等问题。

基于分解的多目标进化算法（Multiobjective Evolutionary Algorithm Based on Decomposition,MOEA/D）由Qingfu Zhang[6]等人提出,该方法将多目标优化问题分解为多个子问题并通过优化每一个子问题来求解。该算法由于收敛速度快,计算复杂度低,性能优异等特点,被众多专家学者研究并应用于医学诊断等诸多领域。因此,本文以长泰枋洋水利枢纽为例,建立了一种水资源优化调度模型,以供水缺额最小以及供水效益最大作为调度目标,并充分考虑水源供水能力、用水户需水限制以及实际应用中的变量非负约束,使用MOEA/D 算法对模型进行计算求解,并从Pareto 解集中优选,得到水资源优化配置方案,以期改善该区域水资源利用效率,助力经济发展。

1 水资源优化调度数学模型

区域水资源调度往往要兼顾经济、社会以及环境等多个方面,所以水资源优化调度其实是一个多目标优化问题。水资源优化调度的数学模型通常被描述为如下形式：

其中D为可行域,D∩Rn,X为n维决策变量,f1（x）,i=1,L,p为目标函数个数。可行域是D满足一系列等式约束和不等式约束条件的所有解的集合。

1.1 目标函数

（1）经济效益目标。以区域内供水经济效益达到最大为目标。表达式为：

式中：bijk为某区域供水带来的效益系数,元/m3,cijk为某区域供水消耗的费用系数,元/m3；xijk为i水源向k分区j用水户输送水量,万m3；qik为i水源向k分区供水顺序系数；φjk为k分区j用水户的用水公平系数；为k分区权重系数；I、J、K分别为水源、分区和用水户总数。

（2）社会效益目标。以供水量缺额最小作为目标,表达式为：

式中：Djk为分区j用水户的需水量,万m3。

1.2 约束及处理

（1）需水能力约束。水源向用户输送的水量应该大于等于最小需水量并小于等于最大需水量,即：

式中：L（k,j）、H（k,j）分别为k分区j用水户需水量的上、下限。

（2）供水能力约束。k分区i水源向所有用水户的输送的水量总量应不大于其可供水量,即：

式中：Wik为k分区i水源可供水量。

（3）变量非负约束。

2 MOEA/D 算法

2.1 权重向量

使用MOEA/D 算法,需要产生一个权重向量来指导后代的选择,权重向量可以通过用Das[7]等提出的systematic approach 方法来获得。在MOEA/D 算法中应用的权重向量应该满足以下要求：

其中,m为目标函数的个数；H为一个用户自定义的整数,表示将每一个维度的目标坐标分割成H份,而权重向量的个数由m和H共同决定,即种群大小和子问题个数也由m和H共同决定,它们均满足。

2.2 聚合方法

本文采用Tchebycheff 法,其表达为：

2.3 约束处理

对于求出的所有Pareto 解集中的所有解,都应满足约束条件。采用如下的惩罚函数处理方法：

式中：α为越界的惩罚系数；V（x）表示目标函数对约束的破坏情况。

显然,对于所有可行解,必须存在V（x）=0；否则,该解就是不可行解。

2.4 目标值归一化

在多目标问题的各个目标中,不同目标函数的结果量纲往往不一致,进而造成可行解不合理的问题。因此需要对各个目标函数进化归一化处理,即：

式中：Fm、F'm分别为目标函数的实际值和归一化值；Fmmin、Fmmax分别为对应目标函数的最小值以及最大值。

2.5 本文算法的步骤

（1）初始化。根据目标函数个数以及自定义整数H确定目标种群数量；初始化权重向量矩阵；种群的随机生成；初始化参考点,参考点为全部个体的每个子目标函数值中的最小值。

（2）进化。利用差分进化算法进行进化操作；修复不合法个体；变异操作增加种群多样性。

（3）评价新个体。计算利用新个体得到目标向量,然后更新参考点。

（4）更新邻域。利用Tchebycheff 聚合方法进行更新。

（5）判断是否为最后一个个体,若是,进入下一步；否则对下一个个体返回（2）。

（6）判断迭代次数是否达到最大,若是,输出最佳前沿、个体以及目标值；否则返回（2）。

3 算例研究

3.1 研究区概况

长泰枋洋水利枢纽工程地处我国福建省漳州市长泰县境内,水系属九龙江北溪龙津溪支流,由上存水库、尚吉电站、溪口闸坝、溪口-许庄引水隧洞4 个部分组成,实现厦门、漳州两市之间的跨区域、跨流域水资源配置。水资源系统概化图见图1。

图1 水资源系统概化图

上存水库年径流量多年平均值为2.53 亿m3,正常蓄水位以下库容1.151 亿m3,兴利库容为1.077 亿m3,为具年调控性质的大（二）型水库。溪口水库年径流量多年平均值为5.24 亿m3,正常蓄水位以下库容216 万m3,兴利库容为30 万m3,为略具日调节性能的小（一）型水库。溪口至许庄引水隧洞全长13.9 km,设计流量10 m3/s,进水口设在溪口水库左岸上游100 m 处,出水口设在厦门市集美区石兜水库的上游河道。石兜水库来水量多年平均值为0.637 亿m3,正常蓄水位以下库容0.332 亿m3,兴利库容为0.319 亿m3,为具有多年调度能力的中型水库。

3.2 需水预测

供水系统中的用水部门主要包括生活用水、生态用水、工业用水和农业用水。本文首先对研究区域内的长泰片以及厦门片进行需水预测,需水预测方法为定额法。

定额法是以社会经济指标和相应的用水定额为参考,通过预测两者的变化,再相乘得到需水量的一种方法。根据《厦门市水资源公报2020》,当年本地人均综合用水量为135 m3,农业亩均用水量为527.5 m3,万元工业增加值用水量为6.6 m3。另外,《2020 漳州市水资源公报》显示,长泰县人均综合用水量406 m3,农田灌溉亩均用水量578 m3,万元工业增加值用水量18 m3。以2020 年为现状基准年,预测生活用水、生态用水、工业用水和农业用水在2025 年的需水量,预测结果见表1。

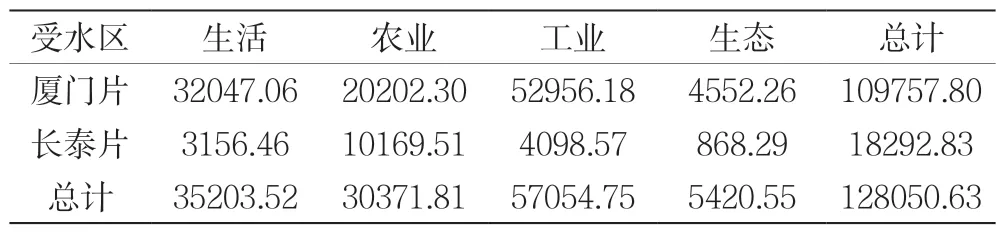
表1 需水预测结果 单位：万m3

3.3 算例参数

根据水资源优化调度模型设置如下参数：

1）效益系数。按照居民用水优先的原则,结合厦门市以及长泰县的实际情况,按照生活、生态、农业、工业的顺序,厦门市供水效益系数（元/m3）为500、500、45、250；漳州市供水效益系数（元/m3）为500、500、26、182。

2）费用系数。费用系数参考厦门市以及长泰县的水价。厦门市生活生态用水为3.2 元/m3,其他用水为3.7 元/m3；漳州市生活生态用水为1.6 元/m3,其他用水为2.0 元/m3。

3）用水公平系数。根据各用水部门的重要程度,本文将生活、生态、农业和生态用水的用水公平系数分别设置为：0.37、0.30、0.10、0.23。

4）MOEA/D 算法参数。设置种群数目为100,最大迭代次数为500。

3.4 结果分析

常规调度由水库调度图来指导水库的调度运行。长泰枋洋水利枢纽水资源系统调度主要是上存水库供水调度。上存水库供水调度图由各个供水对象的控制供水曲线构成,把水库的水位范围分割为几个区段,并按照水库的时段初蓄水情况进行向各个供水对象的分级分量供水。

调度结果见表2。水量、效益。由于厦门市供水水源不止本研究的目标长泰枋洋水利枢纽,因此本研究结果显示的缺水量较多。

表2 调度结果

实验结果表明,对本研究来说,相较于常规调度,基于MOEA/D 的多目标优化调度结果缺水量减少了17.12%；而供水效益增加了34.66%。此研究结果证明了基于MOEA/D 算法的水资源优化调度的可行性与有效性。

4 结论

本文综合考虑供水缺额以及供水带来的效益两个目标,建立水资源优化调度数学模型,采用了MOEA/D 算法来计算求解水资源优化调度模型,并在算法中加入约束处理、归一化及特殊变异操作来改善算法的性能并保持解的多样性。并以枋洋水利枢纽为例,进行水资源优化调度计算,证明了采用本文的利用MOEA/D 算法进行水资源优化调配的可行性。

但实际水资源优化调度还应考虑水质问题,不同水质可应用的部门有所不同,因此,研究水资源优化调度,在这方面还应加强改善。