扭转单壁碳纳米管的第一性原理研究

丁怡 盛雷梅

(上海大学理学院,上海 200444)

1 引言

1991 年日本电子显微学专家Iijima[1]发现了多壁碳纳米管,随后1993 年发现单壁碳纳米管(single-walled carbon nanotubes,SWCNTs)[2],这引发了纳米材料的研究热潮,对其中代表材料碳纳米管的各种物理性质进行实验和理论研究[3−6].1999 年,Fischer 和Johnson [7]提出单壁碳纳米管的电子特性可为小型电子器件提供良好的应用前景,进而为电路中量子尺寸效应的大规模开发提供了碳基芯片的发展方向[8−14],而碳基芯片的一个重要问题便是带隙可控化.

Mazzoni 和Chacham[15]通过第一性原理计算,研究了径向形变对半导体型单壁碳纳米管电子性质的影响,挤压导致单壁碳纳米管带隙从0.92 eV逐渐减小到零.Peng 和Cho[16]通过第一性原理计算,研究了径向形变对半导体型单壁碳纳米管(8,0)电子性能的影响,随着形变程度的增大,单壁碳纳米管首先发生了半导体-金属过渡,进一步形变导致带隙重新打开并诱导了金属-半导体的转变,这种转变是径向形变诱导杂化效应的结果.Shtogun 和Woods[17,18]利用密度泛函理论 (DFT)研究了径向形变和缺陷对单壁碳纳米管性能的影响,并进一步研究了在横向外电场作用下发生径向形变的单壁碳纳米管的电子结构特征.Kang 等[19]研究了空位缺陷对单壁碳纳米管电学性质的影响,结构的变化导致碳管带隙被打开.Berd 等[20]采用强高氯酸处理单壁碳纳米管,通过傅里叶红外变换和拉曼光谱等实验装置进行研究,并通过广义梯度近似和局域密度近似实现第一性原理理论计算,结果共同表明氯原子吸附会导致金属型单壁碳纳米管 (9,9) 产生带隙,从而实现了单壁碳纳米管从金属型向半导体型的转变.Kato 等[21]通过DFT 计算发现手性单壁碳纳米管具有略微扭曲的基态几何形状,扭曲导致手性单壁碳纳米管带隙出现了金属-半导体跃迁.

扭转单壁碳纳米管的分子动力学模拟一直是备受关注的研究方向[22−27],然而分子动力学模拟主要研究单壁碳纳米管的力学性质,并没有研究基态稳定模型与带隙变化规律.本文利用第一性原理密度泛函理论研究扭转单壁碳纳米管,提出了扭转单壁碳纳米管的稳定基态模型,总结了带隙变化的规律,为单壁碳纳米管的带隙可控化研究提出了新的解决方案.

2 模型与计算方法

本文利用第一性原理密度泛函计算软件DSPAW 计算扭转单壁碳纳米管的带隙变化规律.DS-PAW 是Device Studio 平台下的一款第一性原理密度泛函理论(DFT)计算程序,DFT 是基于Hohenberg和Kohn[28]提出的两个基本定理建立,并在Kohn和Sham[29]推导出更严密的方程后发展起来的,其计算核心思路是: 电子密度函数决定了系统的基态物理性质.本文所有SWCNTs 都在周期边界条件下计算,采用共轭梯度近似[30]进行结构优化,赝势选择了PAW 赝势[31],优化的精度设置为10−4eV与0.05 eV/Å,最大优化步长为60,超 胞的 设置 中α=90°,β=90°,γ=120°,3 个坐标轴方向的长度分别为20 Å,20 Å,LZ,其中LZ为超胞在碳管轴向方向的长度,不同碳管模型中LZ是不同的,下文将详细介绍如何确定LZ.k点设置为 (1 × 1 ×kZ),其中kZ根据LZ的大小决定,交换关联函数为PBE[32],能量截止为300 eV,计算过程中没有考虑范德瓦耳斯力.

图1 为(n,m)单壁碳纳米管结构示意图,选取了n+m=8,10,12 这3 类碳纳米带的带隙进行计算,DSWCNT表示碳纳米管的直径,3 类碳纳米带中单壁碳纳米管的直径均在0.5—1.0 nm之间,其中包括手性单壁碳纳米管 (chiral SWCNTs)、锯齿型单壁碳纳米管 (zigzag SWCNTs)和扶手椅型单壁碳纳米管 (armchair SWCNTs),旨在与扭转单壁碳纳米管的带隙变化进行对照.

扭转单壁碳纳米管模型包括了扶手椅型单壁碳纳米管 (4,4),(5,5),(6,6)和锯齿型单壁碳纳米管 (8,0),(10,0),(12,0).扭转模型的构建要遵循两个原则,第一个原则是延管壁方向 (即Z轴方向) 必须是周期性排列并且无限循环.图2 中虚线圆圈的碳原子与实线碳原子之间角度差被定义为最小旋转周期角θperiod(n,m)=360°/n,图2(a)—(f)分别是单壁碳纳米管 (4,4),(5,5),(6,6),(8,0),(10,0),(12,0)的Z轴截面示意图,其θperiod分别为90°,72°,60°,45°,36°,30°.

图2 6 种单壁碳纳米管的最小扭转周期角示意图(a) 90°;(b) 72°;(c) 60°;(d) 45°;(e) 36°;(f) 30°Fig.2.Schematic diagram of the minimum torsional period angle of the six SWCNTs: (a) 90°;(b) 72°;(c) 60°;(d) 45°;(e) 36°;(f) 30°.

图3 更加清晰地表达了扭转单壁碳纳米管需要遵循周期性规律,左边是超胞Ⅰ (Supercell Ⅰ),右边是超胞Ⅱ (Supercell Ⅱ),超胞内每层碳原子绕Z轴旋转不同角度,黄实线上的碳原子在旋转前是平行Z轴分布的,但是旋转后黄实线变为了斜线,可以理解为原子1 (Atom1) 经过一个周期的旋转后到达了原子2 (Atom2) 的位置,超胞Ⅱ内原子2 与超胞Ⅰ内原子3 (Atom3) 在Z轴方向是平行的,并且原子2 等于原子3,这样的扭转模型既能满足单壁碳纳米管是周期性的,也能满足碳原子在Z轴无限排列.

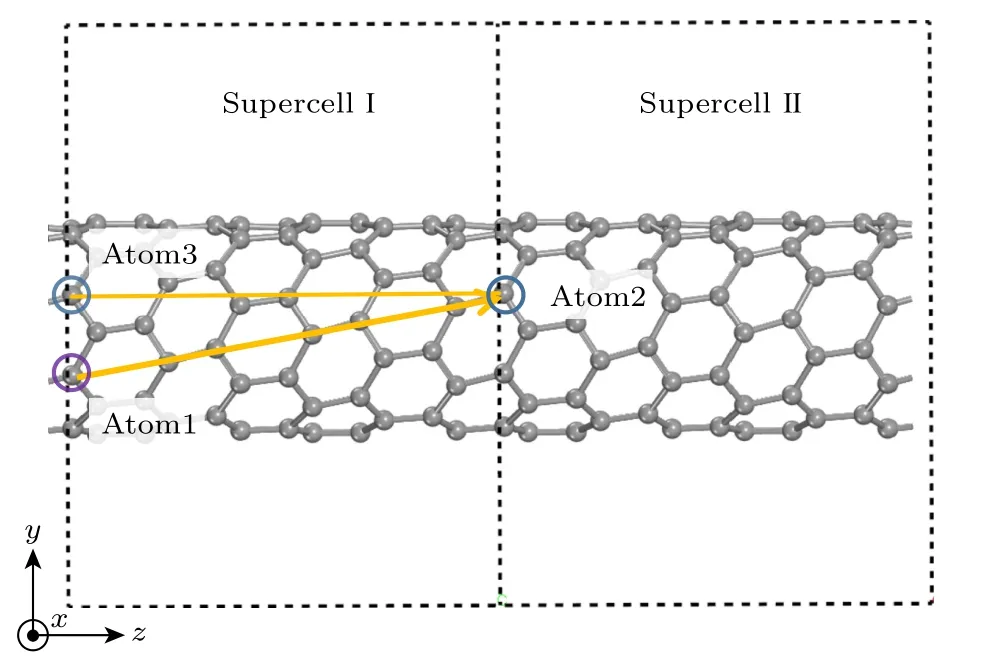
图3 (8,0) 单壁碳纳米管扭转后模型图(扭转强度=3.52 (°)/Å)Fig.3.The (8,0) SWCNT model diagram after torsion(Torsional strength=3.52 (°)/Å).

图4 展示了单壁碳纳米管 (8,0) 扭转模型的构建过程,模型的构建过程参考了Kinoshita 和Ohno[33]的工作,首先定义α为扭转强度 (torsional strength),即单壁碳纳米管在Z轴方向上单位长度的旋转角度,单位是(°)/Å:

图4 扭转 (8,0) 单壁碳纳米管过程示意图Fig.4.Schematic diagram of the torsional process for (8,0)SWCNT.

图4 中原子i绕Z轴旋转θi可得到右侧的旋转模型:

式中zi表示原子i在Z轴方向的坐标,将超胞内所有原子按照图4 旋转θi,即可得到单壁碳纳米管扭转模型.

扭转遵循的第二个原则是由于扶手椅型单壁碳纳米管在Z轴方向是AB 排列,因此超胞Z轴方向上的碳原子数必须是2 的整数倍,而锯齿型的单壁碳纳米管在Z轴方向是ABCD 排列,所以超胞Z轴方向上的碳原子数必须是4 的整数倍.这个原则限制了单壁碳纳米管超胞在Z轴方向的长度,同时限制了LZ,由于每一种单壁碳纳米管的θperiod是定值,所以通过改变LZ就可以改变α,从而得到不同扭转强度下的扭转模型.单壁碳纳米管扭转模型的长度越大,扭转强度则越小,扶手椅型单壁碳纳米管 (6,6) 的长度区间为12.3—44.3 Å,对应的扭转强度区间就是4.88—1.36 (°)/Å.锯齿型单壁碳纳米管 (12,0) 的长度区间为8.5—25.56 Å,对应的扭转强度区间就是3.52—1.17 (°)/Å.更小长度的碳管并没有优化成功,这是因为扭转强度过大,导致碳管失去了周期性结构分布规律.由于受限于模型的原子数,因此更小的扭转强度以及更大的模型无法计算.

3 结果与讨论

图5 展示了扭转(5,5)碳管后典型的能带图与电荷局域密度图,可以看出碳管的带隙在扭转强度为1.62 (°)/Å时被打开,带隙大小为1.02 eV,进一步的扭转则导致了带隙闭合.分析电荷局域密度的变化可以发现扭转确实改变了电荷密度的分布,图中绿色等值面设置为5×10−6e−/bohr3,紫色等值面设置为8×10−6e−/bohr3,扭转强度为1.62 (°)/Å时,紫色等值面明显小了很多,反应到能带图便是带隙变大.但是电荷局域密度图并不能解释所有的能带图变化规律,而带隙的改变也不是完全由电荷局域密度分布的改变而造成,因此本文认为是结构的改变导致带隙的改变.附录图A1 展示了更多碳管的能带图.

图5 扭转 (5,5) 单壁碳纳米管后能带图与电荷局域密度图Fig.5.Change in the band structure and electron localization function of (5,5) SWCNT.

扭转扶手椅型单壁碳纳米管带隙变化规律如图6(a)所示,扭转强度从0 (°)/Å增至7.5 (°)/Å,从下往上3 条曲线分别为扭转单壁碳纳米管 (4,4),(5,5)和(6,6),这3 种单壁碳纳米管的带隙变化均为先增大后减小再增大,发生了3 次相变: 金属型-半导体型;半导体型-金属型;金属型-半导体型.其中,(6,6) 碳纳米管只需要1.6 (°)/Å的扭转强度,带隙就从0 eV 变化到1 eV 左右,图中虚线可对比看出(4,4)与 (5,5) 碳纳米管则需要更大的扭转强度,由于 (6,6) 碳纳米管直径最大,更容易实现扭转,因此 (6,6) 碳纳米管是本文研究的单壁碳纳米管中最理想的带隙可控化结构.目前晶体管的门极长度是衡量半导体技术的关键,假设碳基芯片的门极为一根10 nm 长的扶手椅型碳管 (6,6).根据已知数据预测,为了保证其半导体导电性能,最多需要施加1.36 (°)/Å左右的扭转强度,也就是旋转碳管一个端口136°即可满足芯片需求.

图6 单壁碳纳米管带隙变化图(a) 扶手椅型单壁碳纳米管;(b) 3 类碳纳米带中本征单壁碳纳米管;(c) 锯齿型单壁碳纳米管Fig.6.Band gap variation chart of SWCNTs: (a) Armchair SWCNTs;(b) SWCNTs in three types of carbon nanoribbons;(c) zigzag SWCNTs.

扭转锯齿型单壁碳纳米管带隙变化规律如图6(c)所示,扭转强度从右侧的0 (°)/Å增大到左侧的6 (°)/Å,(8,0) 碳纳米管带隙单调递减,发生了一次半导体型-金属型的相变;(10,0) 碳纳米管带隙先增大后减小,发生了一次半导体型-金属型的相变;(12,0) 碳纳米管带隙单调增大,发生了一次金属型-半导体型的相变.

图6(b)展示了3 类碳纳米带的带隙变化规律,横坐标是不同结构的单壁碳纳米管,纵坐标是单壁碳纳米管的带隙,从下往上3 条曲线分别为n+m=8,10,12.n+m=8 时,单壁碳纳米管的导电性发生了3 次相变: 金属型→半导体型→金属型→半导体型.n+m=10 时,单壁碳纳米管的导电性也发生了3 次相变: 金属型→半导体型→金属型→半导体型.n+m=12 时,单壁碳纳米管的导电性发生了4 次相变: 金属型→半导体型→金属型→半导体型→金属型.

通过图6(a)—(c)横向对比可以看出,扶手椅型单壁碳纳米管带隙变化趋势与3 类碳纳米带中(n,n) 到 (2n,0) 的变化趋势一致,由于扭转强度有极限,因此并没有完全复现3 类碳纳米带的带隙变化趋势.比如,图6(a)中 (6,6) 碳纳米管带隙变化是0→1.2→0→0.6 eV,与之对应的图6(b)中单壁碳纳米管 (6,6)→(7,5)→(8,4)→(9,3)→(10,2)带隙变化是0→0.9→0.8→0.1→0.9 eV,由于 (6,6)碳纳米管扭转强度最大为4.88 (°)/Å,所以带隙并没有继续沿着 (10,2)→(11,1)→(12,0) 而变化.锯齿型单壁碳纳米管带隙变化趋势则与3 类碳纳米带中 (2n,0) 到 (n,n) 的变化趋势吻合,例如,扭转 (10,0)的带隙变化符合 (10,0)→(9,1)→(8,2)的变化规律,并没有复现出 (7,3)→(6,4)→(5,5)的变化规律,原因是扭转强度最大极限为4.23 (°)/Å.

为了进一步分析扭转单壁碳纳米管与3 类碳纳米带的性能变化规律,图7 显示了单壁碳纳米管的直径变化.从图7(a)可看出,扭转扶手椅型单壁碳纳米管的直径随扭转轻度变大单调递增.而从图7(c)可看出,扭转锯齿型单壁碳纳米管的直径单调递减.图7(b)是3 类碳纳米带中单壁碳纳米管直径变化规律,均为单调递增.因此可得出一个结论,扭转单壁碳纳米管的直径变化趋势与3 类碳纳米带中单壁碳纳米管的直径变化趋势相一致.

图7 单壁碳纳米管直径变化图(a) 扶手椅型单壁碳纳米管直径随扭转强度的变化;(b) 3 类碳纳米带中本征单壁碳纳米管直径变化;(c)锯齿型单壁碳纳米管直径随扭转强度的变化Fig.7.Diameter variation chart of SWCNTs: (a) Relationship between diameter and torsional strength for armchair SWCNTs;(b) diameter of SWCNTs in three types of carbon nanoribbons;(c) relationship between diameter and torsional strength for zigzag SWCNTs.

统计单壁碳纳米管优化后的六边形模型平均键长与平均键角如图8 所示.图8(a)表明键长随扭转强度单调递增,其中,扶手椅型单壁碳纳米管键长比锯齿型单壁碳纳米管键长增大更明显,这是因为扶手椅型单壁碳纳米管是AB 排列,而锯齿型单壁碳纳米管是ABCD 排列,所以扭转后,扶手椅型单壁碳纳米管中六边形的形状变化更明显.当扭转强度由0 (°)/Å变化到5 (°)/Å时,增大速率最快的(6,6)碳纳米管,平均键长增大0.04 Å.这是因为如果旋转角度相同,直径越大的单壁碳纳米管,碳原子旋转的距离就越大.最终因为 (4,4) 碳纳米管能够承受最大的扭转强度为7.32 (°)/Å,所以键长增大最多为0.07 Å.图8(b)表明平均键角随扭转强度的变化单调递减,其中,扶手椅型单壁碳纳米管的键角比锯齿型单壁碳纳米管的键角减小更明显,原因是单壁碳纳米管中碳原子排列方式不同.当扭转强度由0 (°)/Å变化到5 (°)/Å时,减小速率最快的是 (5,5) 碳纳米管与 (6,6) 碳纳米管,平均键角减小了0.28 °,而 (4,4) 碳纳米管减小得最多,减小了0.65 °.

图9 为扭转后的形变能变化.其中ET=(Ea-Eb)/Ns,ET表示一个原子的能量变化,Ea表示扭转后体系的能量总和,Eb表示扭转前体系的能量总和,Ns表示超胞内的原子数.可以看出不同种类的单壁碳纳米管在相同扭转强度下有不同的能量变化,但随着扭转强度变大形变能都是单调递增.对于同种单壁碳纳米管来说,直径越大的单壁碳纳米管所需要的能量越多,这是因为单壁碳纳米管的能量变化主要是因为碳原子之间的距离改变.

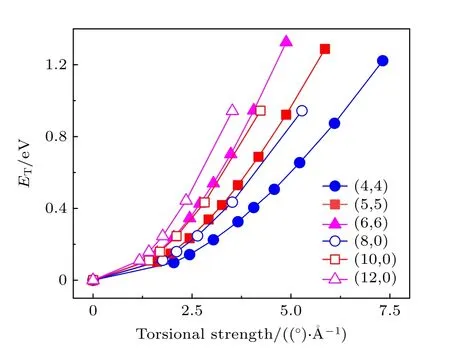
图9 扭转单壁碳纳米管的能量变化图Fig.9.Relationship between energy and torsional strength for SWCNTs.

从图8(a)可以看到,最近邻的碳原子之间平均距离增大,也就是势能增大,因此需要吸收能量.但是对比扶手椅型与锯齿型单壁碳纳米管可以看出,其能量与直径并没有直接联系,原因是体系的能量不仅与碳原子键长有关,也与键角、直径、层间距离有关.

总之,带隙变化是因为结构改变造成的,扭转单壁碳纳米管导致结构发生改变,进而导致了单壁碳纳米管带隙发生变化.单壁碳纳米管带隙变化趋势与对应的碳纳米带变化趋势一致,结构变化也一致,所以我们认为扭转单壁碳纳米管带隙变化是键长、键角和直径等结构因素共同作用的结果.

4 结论

本文通过在Z轴方向上旋转单壁碳纳米管每个原子得到扭转模型,扭转过程中,每种单壁碳纳米管的带隙变化都不一样,但均出现了多次金属型-半导体型或半导体型-金属型的相变,并且扭转单壁碳纳米管的带隙变化趋势与对应的碳纳米带的变化趋势一致.扭转后,扶手椅型单壁碳纳米管的直径单调递增,锯齿型单壁碳纳米管的直径单调递减.通过统计碳原子平均键长与平均键角,发现键长随扭转强度增大而单调增大,键角则随扭转强度增大单调递减.扭转过程中,碳原子的能量单调增大.上述研究结果为单壁碳纳米管带隙可控化提出了新的解决方案,为基于单壁碳纳米管的纳米电子器件和微集成电路提供了理论依据.

附 录

图A1 为本文计算中碳管扭转后典型的能带图,可以看出随着扭转强度的增大,能带图发生了明显变化.

图A1 扭转SWCNTs 后能带图Fig.A1.Change in the band structure of SWCNTs.