快时变信道下基于深度学习的OFDM系统信道估计

季 策, 宋博翰, 耿 蓉, 梁敏骏

(1.东北大学计算机科学与工程学院, 辽宁 沈阳 110169; 2. 东北大学医学影像智能计算教育部重点实验室, 辽宁 沈阳 110169; 3. 东北大学信息科学与工程学院, 辽宁 沈阳 110819)

0 引 言

近年来,随着高速铁路和移动通信的发展,快时变环境下通信系统的研究已然成为热点。为了支持快时变环境下的数据传输,进行准确的信道估计是十分必要的。而正交频分复用(orthogonal frequecy division multiplexing, OFDM)技术,由于其拥有较高的频带利用率和抗频率选择性衰落的能力,已广泛应用于现代通信系统,预计在未来通信网络中也将作为核心技术之一。另一方面,由于多普勒频移和多径效应的影响,信道的快速变化会引起子载波干扰(intercarrier interference,ICI),导致OFDM系统的性能下降。鉴于此,找到一种适应快时变环境的OFDM系统信道估计方法是亟待解决的问题。

对于信道估计算法可分为频域估计算法和时域估计算法,传统的频域算法常采用基于导频辅助的形式,如最小二乘算法(least square, LS)和线性最小均方误差(linear minimum mean square error, LMMSE)算法[1]。其常假定信道的频率响应(channel frequency response, CFR)在导频和数据位置的变化是一种线性关系,然而在快时变环境下这种假设并不成立,因此算法性能较差。时域估计算法采用直接估计出多条路径的信道冲激响应(channel impulse response, CIR)的方式,能更好地减小ICI对信道估计性能的影响。文献[2]提出了基于基扩展模型(basis expansion model, BEM)的时域估计算法,有效提升了时变信道估计的性能。文献[3]提出了基于BEM的扩展卡尔曼滤波(extended Kalman filter, EKF)算法,即EKF_RTSS(rauch-tung-striebel smoother),对比于文献[2],通过在EKF算法后方加入RTSS平滑运算,更好地追踪了信道时域的变化。文献[4] 针对EKF算法的判决反馈矩阵引起的误差传播问题,提出了结合BEM技术的无迹卡尔曼滤波(unscented Kalman filter, UKF)方法,即BEM_UKF,进一步提高了快时变环境下时域信道估计的性能,但由于时域方法需要估计出完整路径的CIR,因此算法复杂度远高于频域方法。

近年来,深度学习算法在无线通信物理层[5-6]得到了广泛的应用,而基于深度学习的信道估计问题,已取得了一定的研究进展。文献[7]提出了一种全连接深度神经网络(fully-connected deep neural network, FC-DNN),将OFDM系统信号检测和信道估计问题进行联合运算,提高了符号的检测能力,但无法提供完整的CFR,因此应用场景受到一定限制。文献[8-9]利用OFDM系统时频面和图像间的相似性,将超分辨率技术应用于信道估计中,利用卷积神经网络(convolution neural networks, CNN)的特征提取能力为OFDM系统的信道估计问题提供了一种有效的方法。但是,上述基于深度学习的频域信道算法都没有考虑快时变环境的影响,因此在性能方面存在不足。文献[10]针对高速移动环境,提出了一种基于BEM的双向长短期记忆(bidirectional long short term memory, BiLSTM)网络,即T-ChanEstNet,有效增强了时域估计算法的性能,并将其网络结构成功扩展到多入多出的系统[11]中。文献[12]在BEM下将快速超分辨率CNN和去噪CNN做级联处理,增强了时变环境下图像超分辨率算法的性能。尽管上述基于BEM的深度学习算法极大地提高了时域估计算法的性能,但是网络结构过于庞大,在复杂度方面仍有改进的空间。

因此,针对上述问题,本文以BEM为基础,提出了一种基于时频特征提取的门控循环(gated recurrent unit, GRU)网络(简称为TF_GRU),由时频特征提取网络和GRU网络两个部分组成。首先,以初始的BEM_LS估计和频域接收信号作为网络输入,利用CNN提取时域和频域的信道特征,并进行特征融合处理,嵌入到下级网络中。其次,通过GRU网络进一步捕捉信道在时间上的变化,网络的轻量化结构使整个系统的复杂度得到了显著的改善。同时,仿真实验表明,本文提出的TF_GRU估计器在性能方面优于其他时域信道估计算法。

1 系统模型

1.1 OFDM系统模型

在OFDM系统中,信道可以被划分成一个时域和频域构成的网格,本文考虑一个子帧中OFDM系统带有T个符号,K个子载波,接收端信号在经过快速傅里叶变换(fast Fourier transform, FFT)后,频域表达式可写成:

Yt=HtXt+Wt,t=1,2,…,T

(1)

式中:Yt∈CK×1、Xt∈CK×1和Wt∈CK×1是第t个符号频域接收、发送信号和信道白噪声;Ht∈CK×K是CFR矩阵,可表示为

Ht=FGtFH

(2)

式中:F∈CK×K为K点FFT矩阵;Gt∈CK×K为第t个符号CIR矩阵,有:

(3)

式中:L为多径数目;ht(k,l)为第t个OFDM符号第l条路径在k时刻的取值。

在慢时变信道下,可认为ht(k,l)在不同采样时刻是相等的,此时Gt为托普利兹矩阵,对应Ht为一个对角矩阵,对角线元素对应各子载波期望的CFR。但在快时变环境中,信道的冲激响应随时间变化,Ht在非对角线处存在干扰项。因此,式(1)可展开成元素相乘的形式为

k=1,2,…,K;t=1,2,…,T

(4)

式中:Yt(k)、Xt(k)和Wt(k)分别是Yt、Xt和Wt的第k个元素;Ht(k,n)为Ht的第(k,n)个元素;第2项为ICI数值。此外,快时变信道存在非平稳特性[13],即信道的时域相关性呈现时变性,各个OFDM符号处的信道关联性较差。因此,传统算法的线性插值运算会使信道估计的性能受限。

1.2 基扩展模型

针对快时变环境,文献[14]已证明时域估计方法的优势,而BEM将CIR变换到基向量张成的低维空间,保证较小的信息损失前提下,降低了时域估计的参数量,因此本文采用BEM作为基本的信道模型。在BEM模型下,式(3)中ht(k,l)可表示为

(5)

Yt=Atct+Wt

(6)

(7)

(8)

2 TF-GRU信道估计算法

2.1 TF_GRU网络

TF_GRU网络结构如图1所示,TF_GRU网络分为两个阶段:① 将信道的时域和频域信息矩阵作为二维(two dimension, 2D)图像处理,利用多级CNN结构粗略提取出快时变信道的图像特征信息。② 采用GRU循环网络结构进一步捕捉各符号之间信道的变化关系,以此来缓解快时变信道的非平稳特性。

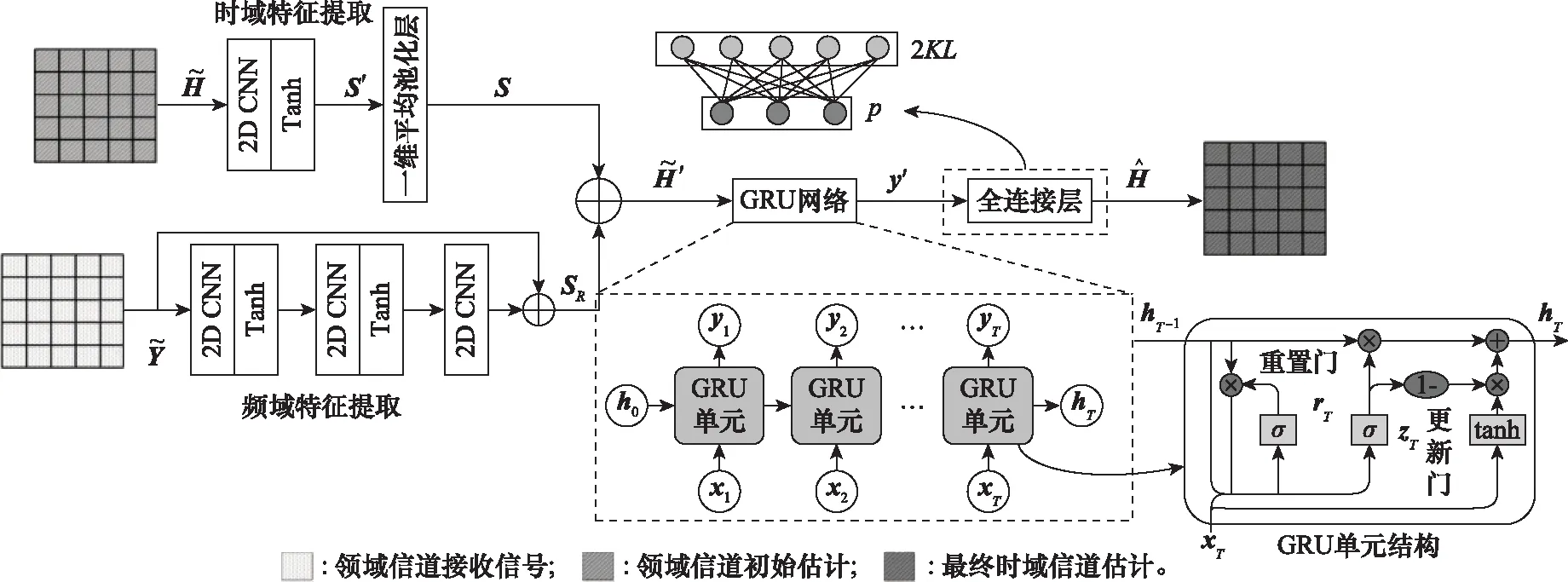
图1 TF_GRU网络原理图

2.1.1 特征提取网络

(9)

(10)

(11)

式中:*代表卷积运算;W∈R3×3为卷积滤波器权重;b∈R3×3为偏置;s∈RTL×2K;tanh为激活函数。考虑到时域估计方法需要评估出完整路径的CIR,因此本文采用一维平均池化层对时域数据进行降维处理,降低计算量,利用滑动窗口对s的每一行做平均处理,在每个OFDM符号处获取多条路径CIR的平均值,平均窗口的大小与信道多径数目L保持一致,步长L,因此输出可表示为s′∈RT×2K。

最后,对于频域特征提取部分,本文采用多级CNN提取频域特征信息,利用较深的CNN层提高网络的特征捕捉能力,首层采用4个卷积核大小为5×5×1的滤波器,保证较低复杂度的同时扩大感受域,第二层采用4个3×3×4核大小的卷积滤波器,深度捕捉信道特征,最后一层CNN有一个5×5×4大小的滤波器,恢复信道矩阵的通道维度, 期间引入残差跳跃连接方式,解决层数增加所带来的梯度爆炸问题[15],假设R代表所有的层数,那么根据式(11),表达式为

(12)

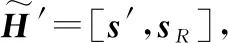
(13)

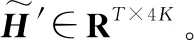
2.1.2 GRU网络

为了更好地追踪快时变信道的变化,学习信道在时间上的相关性是十分必要的。考虑OFDM符号排列与时间序列的相似性,本文采用GRU结构提高时变信道估计的准确度,结构如图1所示。相比于LSTM单元[16],GRU将忘记门和输入门合成了一个单一的更新门,同时混合隐藏状态,在保证性能的前提下,降低了LSTM单元运算复杂度。计算规则如下:

rt=σ(Wirxt+bir+Whrh(t-1)+bhr)

(14)

zt=σ(Wizxt+biz+Whzh(t-1)+bhz)

(15)

nt=tanh(Winxt+bin+rt⊙(Whnh(t-1)+bhn))

(16)

ht=(1-zt)⊙nt+zt⊙h(t-1)

(17)

式中:ht、xt、rt和zt为t时刻GRU的输出、输入以及重置门和更新门;⊙代表元素乘积;Wir、Wiz、Win∈Rp×d、Whz、Whr、Whn∈Rp×p为权重矩阵;bir、bhr、biz、bhz、bhn、bin∈Rp×1为偏置向量;p和d分别为GRU的隐藏单元维度和输入信号维度。如图1所示,首先,将特征融合后的每个OFDM符号信道处的数值作为GRU 单元的输入,GRU单元的个数为一个子帧中OFDM符号的数目T,每个GRU单元利用内在的门结构预测符号处的信道变化,并将此阶段的预测结果传输到下一个符号处,关联相邻信道的变化关系。因此,GRU网络最后的输出向量可表示为

何谓凸显？凸显(prominence)原来是听觉语音学的一个术语，指一个音或音节在其环境中比其他音或音节突出的程度。“凸显”在认知语法研究领域成为一个常用术语，但是其用法还是指某个成分在句中的突出程度，比如，形容词性谓语句“学生多”这样单个形容词作谓语的句子，一般不能单说，而一旦将其用于对比、比较的语境中，就可以了，如“学生多，老师好，学校的操场也不小”，就很自然了，为什么呢？冯胜利(2011)认为这是由汉语韵律结构对语法的制约使然，但是我们认为，形容词谓语句是描写语体的典型句型，描写语体要求对场景的状态进行描述，对场景中的若干个事物进行凸显，所以一般不出现形容词谓语句单用的表达形式。

(18)

式中:fGRU(·)和ΘGRU代表GRU网络的传输函数和全部训练参数;y′∈RT×p为一帧的输出;h0为初始隐层状态,默认为零向量。其次,需要注意,采用不同的p值会使得GRU网络的输出维度与信道标签值不一致,因此本文引入了全连接网络对输出信号的维度进行重新调整,利用神经元个数调整输出信号的维度。因此,全连接层的输入和输出神经元个数分别为p和2KL,计算过程可表示为

(19)

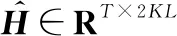
2.2 训练与测试过程

据第2.1节,在获得CIR估计值之后,本文以最小化均方误差(mean squared error, MSE)方式来训练两个网络的参数,损失函数定义为

(20)

式中:S和H∈RT×2KL分别为训练样本数目和真实的CIR。为了加快训练的收敛性,采用自适应矩估计(adaptive moment estimation, Adam)算法更新网络的参数集,测试数据和训练数据具有相同形式,在加载离线训练后的网络参数后,在线预测CIR值。这里迭代次数(epoch),批量大小(batch)和初始学习率分别设置为100,50和0.001。

3 仿真分析

3.1 仿真参数设置

对于离线训练过程,本文的数据集来自具有7条路径的瑞利衰落信道(Rayleigh fading channel)通信链路,每条路径均具有Jakes频谱的特性[17],OFDM系统的参数配置如表1所示。

表1 系统参数

在下文中,除非特殊说明,其余参数均按表1选取,移动端测试速度默认为250 km/h。对于训练数据集,将14个OFDM符号作为一个子帧,在20 dB信噪比情况下产生15 000个子帧数据,其中12 000个作为训练集,3 000个作为验证集。另一方面,对于测试集,在更广泛的信噪比情况下生成600个数据进行仿真结果的测试,测试结果分别与BEM_LS[2]、BEM_LMMSE[2]、BEM_EKF_RTSS[3]、BEM_UKF[4]、T-ChanEstNet算法[10]进行对比,算法规格均按原文要求选取。

3.2 移动端速度对估计性能的影响

为了证明快时变环境对信道估计性能的影响,图2和图3分别对比了各算法在100 km/h和300 km/h两种不同的移动端速度下的归一化MSE(normalized MSE, NMSE)性能和误码率(bit error rate, BER)性能。

图2 不同移动端速度下的NMSE性能比较

从图2可以看出,在不同高速环境下,对比其他时域算法,TF_GRU算法拥有更好的NMSE性能,并且随着移动端速度提升,TF_GRU算法有着最小的NMSE误差损失。这是因为TF_GRU网络虽然不能完全消除信道变化引起的估计误差,但能够有效学习信道的时间相关性。从图3可以看出,在100 km/h的速度下,BEM_UKF, T-ChanEstNet、BEM_EKF_RTSS和TF_GRU算法有着相近的性能,同时优于其他算法。随着移动端速度上升,两种深度学习方法和BEM_UKF算法拥有较好的BER性能和较小的BER性能损失。但值得注意的是,在相同条件下,TF_GRU算法拥有更低的运算复杂度。因此,实验证明了TF_GRU网络在高速环境下的优势。

3.3 导频数量对估计性能的影响

图4和图5分别对比了不同算法在300 km/h移动端环境,导频数量变化情况下的NMSE性能和误码率BER性能。

图4 不同导频数量下的NMSE性能比较

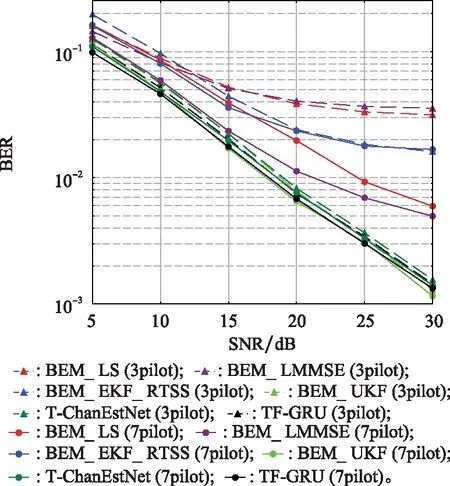
图5 不同导频数量下的BER性能比较

在图4中,当每个符号处占用7个子载波资源时,对比于其他算法,TF_GRU算法的NMSE性能最好,并且值得注意的是:随着导频子载波数目减少到3,BEM_LS, BEM_LMMSE, BEM_EKF_RTSS 3种传统时域算法的NMSE性能变化较大,证明了它们对导频先验信息的依赖性。在图5中,TF_GRU算法依旧保持较好的BER性能,证明了TF_GRU算法对于导频资源的数目变化有着较强的鲁棒性,即能以较低的性能损失节省导频资源。

3.4 调制方式对于估计性能的影响

在信道估计中,由于均衡数据符号的能力与调制方案联系较为紧密,而在高阶调制环境下,误差传播问题更为严重。因此,为了进一步证实在快时变环境下TF_GRU网络的优势,图6比较了在16QAM和64QAM两种高阶调制方式下各类算法的BER性能。

图6 不同调制方式下的BER性能比较

从图6可以看出,无论是16QAM还是在更高阶的64QAM调制方式下,对比其他算法,TF_GRU在保证低复杂度的前提下均能获得较好的BER性能,可见TF_GRU网络在高阶调制环境的性能优势。

3.5 复杂度分析

对于算法的运算复杂度,本文采用一个子帧中OFDM符号进行的实值乘法运算次数作为衡量指标。首先,假定K′为实际输入子载波数目,Q和L为基向量维度和多径数目。因此,BEM_LS的复杂度为56(QL)2K+QLK。

其次,对于时域特征提取部分,卷积核的大小为3×3×1,因此一帧的计算复杂度为192LK,对于频域特征提取部分,一帧的计算复杂度为9 632K,针对GRU单元,根据式(14)～式(17),需要3(2K′·p+p2)+2p次实值乘法。为了获取隐层更新状态,额外需要2p次乘法运算。因此GRU单元共需3(2K′·p+p2)+4p次实数乘法运算,再带入K′=4K,p=2K后,一个子帧中的GRU网络复杂度为840K2+112K。对于全连接层,根据式(19),复杂度为10 080LK,因此在考虑到BEM_LS算法的初始估计对复杂度的影响,总复杂度可表示为:56(QL)2K+QLK+840K2+10 272LK+9 744K,代入具体参数后算法总复杂度如表2所示。可以看出,BEM_LS拥有最小的复杂度,但性能并不理想,TF_GRU相比于其他方法,在保证性能的前提下,较为显著地降低了在测试过程中的运算量。

表2 算法复杂度对比

4 结束语

本文针对快时变环境下的OFDM系统信道估计问题进行了研究,引入了一种TF_GRU网络结构。实验结果表明了本文所提出的算法可有效提取信道之间的变化特征,与其他算法相比,在快时变环境下展示了较好的性能优势,并且有效降低了运算的复杂度。在未来的工作中,可以尝试将更前沿的循环网络结构加入信道估计中,并将网络构建为一种端对端的符号检测器,能否实现更好的BER性能还值得探索。