基于位置观测信息的Davenport四元数DVL标定方法

唐洪琼, 许江宁, 史文策,2, 何泓洋, 李方能,*

(1. 海军工程大学电气工程学院, 湖北 武汉 430033; 2. 中国人民解放军91321部队, 浙江 金华 322000)

0 引 言

自主式水下航行器(autonomous underwater vehicle, AUV)广泛应用于国家海防建设、海洋资源勘探等军民领域,高精度、高可靠性的自主导航能力是AUV顺利完成任务的前提[1-3]。捷联惯性导航系统(strapdown inertial navigation system,SINS)由于结构简单、体积小、隐蔽性强、便于与其他设备集成化设计等优点,在水下定位导航与授时(position, navigation and timing, PNT)领域受到广泛关注,成为AUV自主导航定位的重要手段[4-6]。然而,SINS本质上是以牛顿第二定律为基础的积分推算系统,需要对惯性测量单元(inertial measurement unit,IMU)的输出进行积分运算,导致其导航误差会随着时间的推移而不断积累[7-9]。水下环境对全球导航卫星系统(global navigation satellite system, GNSS)信号具有屏蔽作用,而多普勒计程仪(Doppler velocity log,DVL) 测速精度稳定,可为SINS提供实时外部速度辅助融合信息,SINS/DVL组合导航已成为当前解决水下导航问题的主流方案[10-12]。

DVL通过声学多普勒效应来测量AUV相对于水底或者水流的速度,在工程实际中,由于制作工艺、外界环境、安装偏差等条件限制,导致DVL的测速误差难以避免[13-14]。因此,在预先标定DVL误差参数的基础上,通过标定结果对DVL原始输出进行实时补偿以确保速度量测信息的准确性对提高SINS/DVL组合导航系统的精度具有重要意义[15-16]。

近年来,为实现DVL误差参数的准确标定,众多学者对此展开了研究。刘德铸等[17]将最小二乘法应用于标定DVL安装误差角,并通过浅海试验验证了所提方法的有效性,但此方法无法实现对刻度因子误差的标定,一定程度上影响了DVL的量测精度。Li等[18]将DVL误差标定问题转化为求取两组矢量间的旋转参数问题并通过基于奇异值分解(singular value decomposition, SVD)的最小二乘估计法实现了对其的求解,但当AUV处于非匀速直线运动时,该标定方法的效果会变差。Lyu等[19]将DVL误差作为系统状态参数利用卡尔曼滤波(Kalman filter,KF)进行实时估计实现了DVL的在线自标定,但当AUV处于不同的机动状态时,状态量的可观测度难以得到保证。徐晓苏等[20]构建了GNSS/SINS/DVL组合导航系统,提出了一种基于梯度下降(gradient descent, GD)四元数理论的标定方法,仿真和车载试验结果都验证了方法的有效性。Wang等[21]在GD法的基础上,利用二阶拟牛顿(quasi-Newton, QN)法替代一阶GD法以加快误差收敛速度,并分别基于速度和位置观测信息提出了两种标定方法,车载和船载试验结果表明基于位置观测信息的标定方法效果更佳,但方法中的权值系数通常被设定为经验值,导致该方法在不同条件下的普适性收到了制约。随着机器学习的快速发展,基于智能算法的标定方法开始出现。Wang等[22]利用遗传算法(genetic algorithm, GA)和支持向量回归(support vector regression, SVR)搭建回归预测器来标定DVL,该方法无需预先建立模型且适用于标定大安装误差角。Li等[23]利用改进的粒子群优化(particle swarm optimization, PSO)算法实现了对DVL刻度因子误差和安装误差角的估计,并设计仿真和船载试验验证了标定方法的有效性。但是,Wang和Li等的标定方法参数设置复杂且计算量庞大,导致实时性效果不佳。

基于上述研究,本文提出了一种基于位置观测信息的Davenport四元数方法以实现对DVL刻度因子误差和安装误差角的标定工作,首先,通过基于多普勒测速原理的位置观测推算来标定刻度因子误差。而后,利用基于Davenport四元数方法的位置观测矢量方程解算来标定安装角误差。所提方法相较于现有方法,无需设置初始值,不依赖于特定轨迹和准确的先验知识,更具普适性。船载湖试对比分析了该标定方法与其他方法的标定效果,结果表明,在简单和复杂不同的机动情况下,该标定方法得到的速度精度更高,同时,利用标定补偿后的DVL输出进行SINS/DVL组合导航,该方法得到的位置误差更小。

1 DVL测速误差分析与建模

定义坐标系:选取“东—北—天(E-N-U)”地理坐标系为导航坐标系,记为n系;选取“右—前—上”坐标系为载体坐标系,记为b系;DVL安装坐标系记为d系;地心惯性坐标系记为i系;地球坐标系记为e系;计算导航坐标系记为n′系。

在理想的安装情况下,DVL安装坐标系d系与载体坐标系b系的坐标轴应该是互相一致的,即安装矩阵为单位阵I3×3,但在工程实践中,由于技术工艺限制导致安装误差角难以避免,载体上DVL安装误差示意图如图1所示,其中,xb-yb-zb表示b系,xd-yd-zd表示d系。

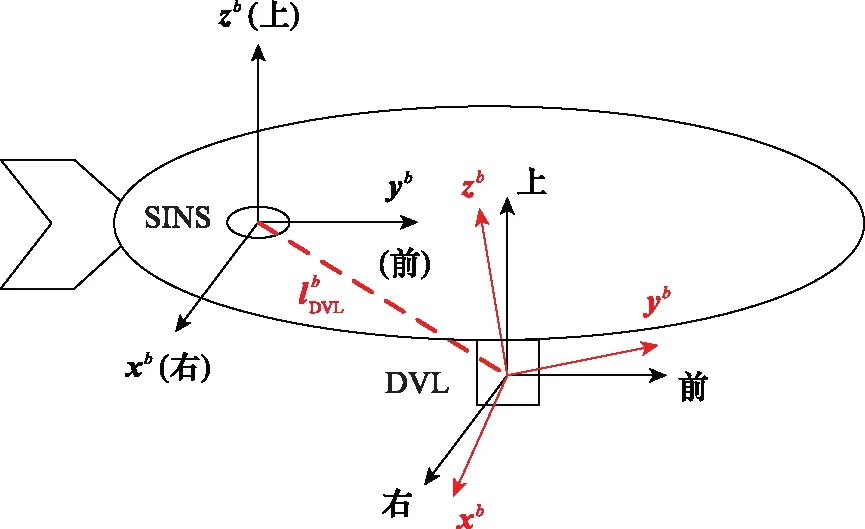
图1 DVL安装误差示意图

根据DVL的工作原理,其测速误差模型[24]可表示为

(1)

在实际工程应用中,由于SINS和DVL之间通常紧密安装且杆臂矢量可直接通过测量获得并予以补偿[25],因此本文将忽略杆臂误差的影响,式(1)可简化为

(2)

(3)

(4)

2 标定方法基本原理

在本文所提的DVL误差标定系统中,当AUV处于水面航行状态可接收GNSS信号时,利用KF最优估计方法进行SINS/GNSS组合导航,得到载体高精度的姿态和速度信息作为参考值,然后综合DVL测量的d系下的速度值,通过标定算法估计出刻度因子误差和安装误差角并对DVL输出进行补偿。DVL误差标定系统结构如图2所示。

图2 DVL标定系统结构图

2.1 刻度因子误差的标定

由于姿态旋转矩阵的模值为1,即姿态旋转矩阵与向量相乘时,只会改变向量的方向但不改变向量的大小。因此,同时对式(4)两侧进行取模可得

(5)

此时,在DVL测量得到载体d系速度的基础上,可以得出:

(6)

但需要指出的是,在利用式(6)计算刻度因子误差时,由于直接使用DVL输出的量测值会引入量测噪声误差,进而降低了刻度因子误差的标定精度。因此,为进一步消除DVL量测噪声的影响,同时对式(4)两侧进行位置运算,此时,式(4)的左侧可表示为

(7)

式中:k表示某一离散时刻;Δt表示采样时间间隔。

设在DVL每次采样时间间隔Δt内,SINS/GNSS组合导航系统解算更新n次,此时,对位置信息进行离散化处理可得式(4)的右侧为

(8)

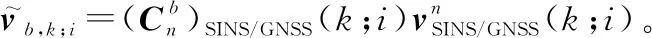
因此,可以得出基于位置信息的刻度因子误差s表达式为

(9)

2.2 安装误差角的标定

利用式(4)和式(9),可以得到基于位置信息的安装误差角计算表达式为

(10)

令:

(11)

此时,式(10)将变换为

(12)

(13)

式中:ωk为量测向量对应的权值,在本文标定问题中,ωk=1。

为快速准确地完成DVL安装误差角标定,采用Davenport四元数方法[28-29]对旋转矩阵R进行求解。

在式(13)中,由于常数对目标函数的最小化不产生任何影响,对其进行线性变换后可以得到:

(14)

(15)

忽略常数项,目标函数f可以进一步化简为

(16)

由于矩阵的迹运算对目标函数不产生影响,根据矩阵迹的性质可以得到:

(17)

旋转矩阵R可用四元数形式表示为

(18)

式中:q0和q分别为四元数的标量部分和矢量部分。此时,目标函数可改写为

(19)

根据矩阵迹的性质,对式(19)作进一步运算:

(20)

对于tr([q×]AT)而言,将其展开可得

tr([q×]AT)=q(1)(A(3,2)-A(2,3))+q(2)(A(1,3)-
A(3,1))+q(3)(A(2,1)-A(1,2))

(21)

令:

(22)

则式(21)可化简为

tr([q×]AT)=-aTq

(23)

将式(23)代入式(20)可得

(24)

设tr(A)=ρ且A+AT=B,式(24)可变换为

(25)

根据矩阵运算法则,式(25)可改写为线性形式:

(26)

式中:Q为矢量部分在前的四元数形式的姿态矩阵;D为Davenport矩阵。

基于上述推导,目标函数f化简为minf(Q)=-QTDQ且QTQ=1,采用拉格朗日乘数法对目标函数f最小化问题进行求解,则

minf(Q,λ)=-QTDQ+λ(QTQ-1)

(27)

对方程进行求导得

DQ=λQ

(28)

因此,Q为D的对应于特征值λ的特征向量。此时,姿态四元数目标函数f最小化问题转化为求解矩阵D的最大特征值对应的特征向量的问题,在求出Q的基础上,将其转换为欧拉角即为所标定出的DVL安装误差角。

3 试验验证

为验证本文所提DVL标定方法的可行性和有效性,位湖北省武汉市木兰湖开展了船载湖试试验。船载导航设备包括CY-JG90J型捷联惯性导航系统、PA600型DVL传感器和GNSS接收机,设备的参数如表1和表2所示。试验过程中以高精度实时动态定位(real-time kinematic,RTK)-GNSS与SINS进行组合后得到的结果作为参考基准。主要试验设备实物图以及试验平台安装概况如图3所示。

表1 CY-JG90J型SINS的性能参数

表2 PA600型DVL的性能参数

图3 试验平台搭建全景

此次船载试验共采集12 000 s实测数据,其中,0～1 200 s为SINS初始对准阶段,以满足后期高精度组合导航的基本需求。选取初始对准阶段后的两段1 200 s试验数据对不同机动条件下DVL标定效果进行验证,所选两段时间内DVL的原始输出数据和对应的试验船行进轨迹如图4和图5所示。其中,黄色图标表示轨迹起点,绿色图标表示轨迹终点。

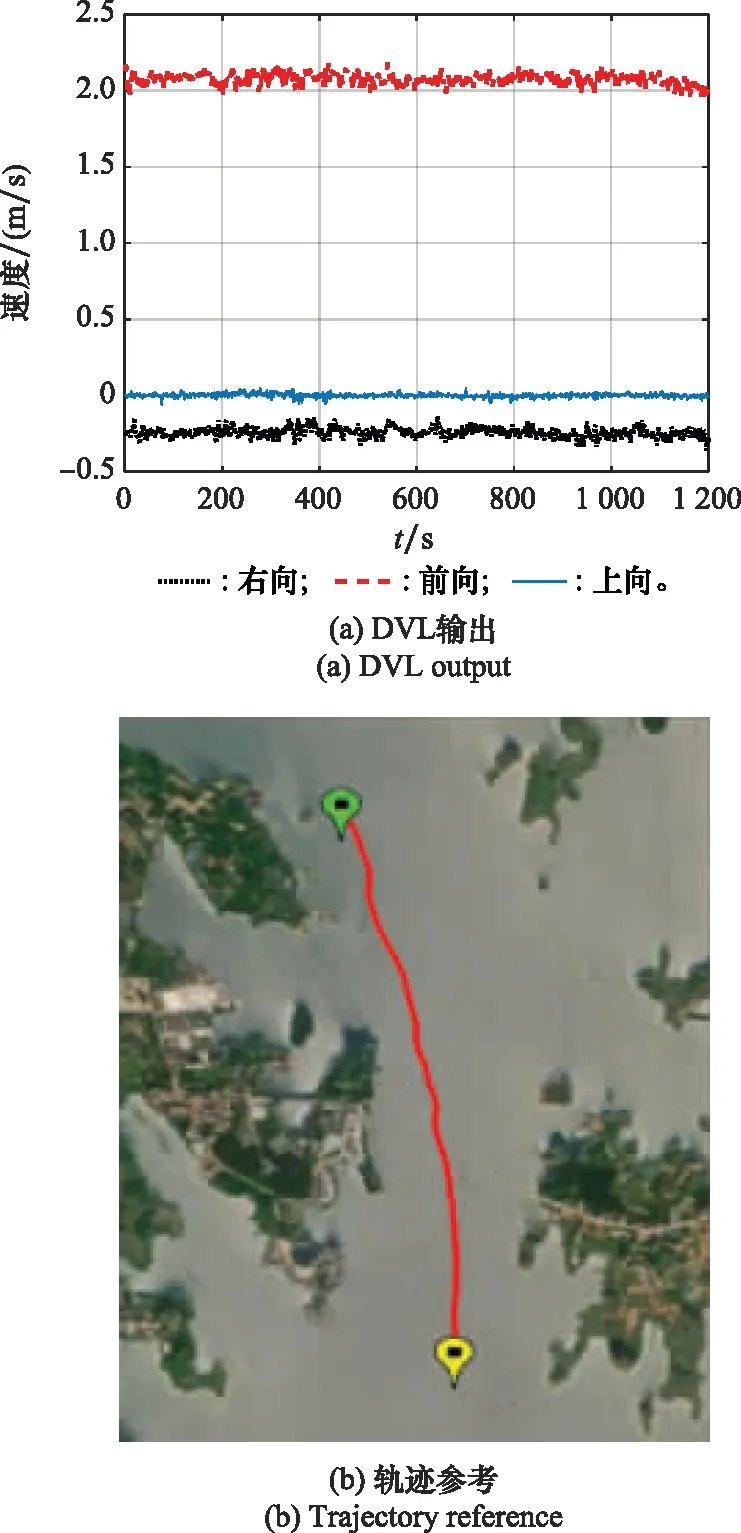
图4 简单机动情况下的DVL原始输出及对应轨迹

图5 复杂机动情况下的DVL输出及对应轨迹

3.1 简单机动情况下的性能验证

利用图4所示轨迹验证载体在简单机动情况下的DVL标定效果。为比较方法性能,分别利用SVD标定方法、KF标定方法、基于位置观测信息的拟牛顿标定方法和本文所提的标定方法进行1 200 s的标定试验,利用标定结果对DVL测量输出进行补偿,并将补偿后的结果与GNSS/SINS组合导航得到的DVL参考速度进行对比,得到3个方向的速度误差结果如图6～图8所示。为方便表述,上述4种标定方法分别记为SVD、KF、拟牛顿四元数位置规则(qusai-Newton quaternions position, QNQ-P)和Davenport位置(Davenport position, DP-P)。

图6 简单机动时右向速度标定误差

图7 简单机动时前向速度标定误差

图8 简单机动时上向速度标定误差

从图6～图8可以看出,对右向速度而言,4种标定方法补偿后的误差相对于未标定数据均有了提升,SVD和KF方法误差基本稳定在0.1 m/s以内,QNQ-P和DP-P方法误差基本稳定在0.08 m/s以内,但DP-P方法标定误差更加平滑。对前向速度而言,由于试验载体行进过程中主要为前向速度且速度量测值不可避免地受外界噪声影响,所以误差结果波动较大,但相比于未标定和KF方法标定误差,另外3种标定方法所得误差更小。对上向速度而言,由于KF标定方法的天向通道发散,导致最终标定结果不可信,而SVD、QNQ-P和DP-P方法标定误差效果基本相当。总的来说,由于简单机动情况下的试验载体近似作匀速直线运动,KF方法中部分状态量的可观测度较弱[30],因此导致KF方法的标定效果大幅下降,而其他3种标定方法的速度误差均能基本稳定在0.1 m/s以内,能够满足后续组合导航的要求。

为量化比较方法效果,选取1 200 s内速度的最大绝对误差MAX和平均绝对误差(mean absolute error, MAE)作为性能评判指标,MAE定义如下所示:

(29)

最终计算结果如表3所示,可以看出,当试验载体进行简单机动时,KF方法的标定结果不够理想,仅有右向速度误差优于未标定值,而SVD、QNQ-P和DP-P方法的速度标定误差在各个方向上均优于未标定值,达到了速度标定的目的。

表3 简单机动时不同标定方法速度误差标定结果

为进一步比较方法效果,利用SVD、QNQ-P、DP-P方法标定补偿后的DVL量测输出与SINS通过标准KF算法进行组合导航得到位置结果,并与KF标定方法进行对比以间接反映标定效果的优劣,试验得到的轨迹结果以及位置误差如图9、图10和表4所示。

表4 简单机动时位置误差的最大值与平均值

图9 简单机动时试验载体轨迹对比图

图10 简单机动时位置误差对比图

其中,位置误差[31]的计算公式如下:

(30)

式中:ΔP表示位置误差;L表示纬度;λ表示经度。

由图9可知,使用未标定的速度进行组合导航得到的轨迹发散严重,而通过标定技术对DVL输出进行补偿后再进行组合导航的轨迹均能较好地跟踪参考轨迹。需要指出的是,使用KF方法得到的位置信息准确度较高,说明当试验载体近似作匀速直线运动时,位置状态量不同于安装误差角状态量,其可观测度并没有受到影响。

由图10可知,使用QNQ-P和DP-P方法标定后的速度进行组合导航得到的位置误差精度相当且明显优于其他方法,但DP-P方法的误差曲线更加平滑。

表4可以更加直观地反映位置误差结果,从表中可以看出,相比于其他方法,QNQ-P和DP-P方法的标定效果有了大幅提高且幅度均达到80%以上,而DP-P方法的导航精度更高,以位置误差最大值为例,比QNQ-P方法进一步提高了27.94%。试验结果验证了所提DP-P标定方法在试验载体简单机动情况下的有效性。

3.2 复杂机动情况下的性能验证

利用图5所示轨迹验证载体在复杂机动情况下的DVL标定效果。利用不同标定方法得到的DVL测量输出与DVL参考速度进行比较,得到3个方向的速度误差结果,如图11～图13和表5所示。

表5 复杂机动时不同标定方法速度误差标定结果

图11 复杂机动时右向速度标定误差

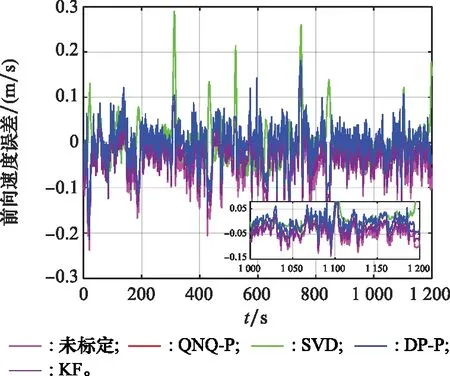
图12 复杂机动时前向速度标定误差

图13 复杂机动时上向速度标定误差

从图11～图13可以看出,当试验载体作连续“S”形的复杂机动时,SVD方法的标定效果出现了下滑,速度误差曲线波动剧烈;KF方法中安装误差角状态量的可观测度增强,右向和前向速度的标定误差结果明显优于简单机动情况,上向速度由于天向通道发散的原因,标定结果仍然不可信;QNQ-P和DP-P方法标定精度基本相当且优于其他方法,但DP-P方法的速度误差曲线波动范围更小。从表5可以看出,当试验载体进行复杂机动时,与未标定的速度误差相比,使用4种标定方法后的速度误差均有不同程度的降低,但就整体而言,本文所提DP-P方法的标定效果最佳。

利用不同方法标定后的速度进行组合导航,得到的轨迹结果以及位置误差,如图14、图15和表6所示。

表6 复杂机动时位置误差的最大值与平均值

图14 复杂机动时试验载体轨迹对比图

图15 复杂机动时位置误差对比图

由图14和图15可知,使用未标定的速度进行组合导航得到的轨迹与参考轨迹存在较大偏差;使用SVD方法标定补偿后的速度进行组合导航,位置误差随着时间的推移而逐渐增大;使用KF、QNQ-P和DP-P方法标定补偿后的速度进行组合导航,1 200 s内的位置误差基本均能控制在20 m以内。表6进一步说明了KF、QNQ-P和DP-P方法在导航精度方面所存在的优势,相比而言, DP-P方法的精度更高,以位置误差平均值为例,比KF方法提高了62.74%,比QNQ-P方法提高了10.94%。虽然DP-P方法的速度标定精度与QNQ-P方法相当,但导航定位精度更高,进而表明该方法标定的DVL误差参数准确度更高。试验结果验证了所提DP-P标定方法在试验载体复杂机动情况下的有效性。

4 结 论

本文针对DVL刻度因子和安装误差角严重影响SINS/DVL组合系统导航精度的问题,提出了一种基于位置观测信息的Davenport四元数方法,并将其应用于DVL预标定系统。通过船载湖试试验验证了方法的有效性,简单和复杂不同的机动条件下,所提标定方法在准确度和稳定性方面均具有优越性,具有良好的工程应用价值。