基于可控域的定点返回轨道全局敏感性分析

王 奇, 陆 林, 李海阳,*, 杨路易

(1. 国防科技大学空天科学学院, 湖南 长沙 410073;2. 空天任务智能规划与仿真湖南省重点实验室, 湖南 长沙 410073)

0 引 言

月球作为距离地球最近的天体,是人类进行深空探测的重要中转站[1-2]。近年来,随着航天探测技术的不断进步,月球的应用价值和开发潜力逐步显现,世界各主要航天国家纷纷将下一步的航天目标投向月球[3-4],其中包括“阿尔忒弥斯”计划[5]、“嫦娥工程”计划[6-8]等。新一轮探月热潮将主要目标集中在载人月球探测,并最终进行月球基地的建设[9]。在任务过程中,对于从月球返回地球的航天器,不仅需要确保航天员可以安全返回地球,同时为了最小化回收资源,以便对航天员进行快速搜救、开展航天器回收工作,客观上要求航天器可以准确地返回指定的着陆场。由于定点返回轨道涉及到较多的约束参数,并且各参数之间的影响程度各不相同,这对定点返回轨道的进一步认识和理解带来了困难。因此,针对定点返回轨道的相关参数进行深入的参数敏感性分析对于未来的月球探测任务具有重要意义。

参数敏感性分析是一种基于数学统计来研究数学模型的方法,通过对系统数学模型进行研究,可用于确定系统的各个不确定性输入对模型不确定性输出的影响程度[10-11],广泛运用于水文过程模拟[12]、材料结构分析[13]、风险评估[14]等领域。运用参数敏感性分析方法可以进一步对定点返回轨道的参数敏感性特性进行分析,确定对返回轨道影响较高的参数,从而为后续的轨道优化设计提供参考。

目前,已有诸多学者对月地返回轨道问题进行了研究,文献[15]基于双二体假设动力学模型,对月地返回轨道特性进行了一定程度的分析。文献[16]利用非线性规划算法优化求解了不同机动方案的月球逃逸轨道。文献[17]结合三体问题模型,运用兰伯特算法求解了航天器在环月飞行阶段的返回问题。文献[18]针对月地返回飞行任务,提出了一种双重优化算法的两层串行求解策略。文献[19]提出了一种利用单脉冲和三脉冲机动方案构造月地返回轨道的方法。文献[20]针对返回近地空间站的月地转移轨道优化问题,提出了一种基于改进的多圆锥曲线的高精度轨道设计方法。文献[21]在考虑满足给定约束条件的情况下,通过一种返回轨迹的构建算法构建了从月球返回地球大气层再入点的单脉冲和三脉冲轨道机动方案。上述研究大多基于一般月地转移轨道,在定点返回轨道的研究方面。文献[22]采用多起点算法对单脉冲定点返回轨道进行了优化求解,但搜索近乎遍历,效率不高。文献[23]针对载人月球极地探测任务,对定点返回轨道优化设计问题进行了研究。文献[24]提出了一种解析方法来快速生成单脉冲定点返回轨道的初始解。文献[25]针对三脉冲返回轨道方案,提出了一种从初步计算到精确计算的串行求解策略。文献[26]基于单脉冲月地返回轨道的可达域分析,推导了返回轨道存在性判据,并给出了单脉冲定点返回轨道的多层快速迭代设计方法。上述研究针对定点返回轨道的设计方法和轨道参数相关特性进行了分析,但尚未对定点返回轨道的可控域问题进行深入的研究。

定点返回轨道可控域表征了可行解的空间范围,可作为可达域问题[27]的逆问题进行求解,相关结果可直接用于相关的空间任务分析和设计。对于地月空间的可达域问题,文献[28]提出了精确可控域数值延拓方法,系统研究了载人登月各阶段轨道的可达域问题。文献[29]对从地月南向近直线晕轨道出发的载人奔月轨道到达月面的可达域特性进行了分析。文献[26]基于近月伪参数对一般月地返回轨道的可达域进行了分析,但未进一步分析定点返回轨道的可达域。可以看出,目前关于可达域问题的研究较多,而较少有针对可控域问题进行研究。由于近月点参数的可控域直接决定了定点回轨道的可行解范围,因此直接基于定点返回轨道的可控域进行参数敏感性分析,可以得出在可行的空间范围内各参数之间的影响程度。同时,目前关于区间的全局敏感性分析方法大多基于空间采样进行计算,而定点返回轨道的可控域为在约束条件下的有限区间范围,直接采用空间采样方法会对结果造成较大的误差,因此需要进一步发展一种针对可控域的敏感性分析方法,从而更准确的反映出可控域范围内的参数敏感性特性。

基于上述考虑,本文针对给定约束条件下的定点返回轨道,具体分析了近月点参数的可控域分布范围。并在定点返回轨道可控域分析的基础上,以参数可控域集合点为初始计算点,提出了一种基于可控域的参数敏感性分析方法。在仿真分析中,给出了定点返回轨道近月点参数的可控域分布规律,并基于提出的可控域敏感性分析方法,详细分析了在可控域空间范围内各主要参数间的影响程度,给出了各参数间的敏感性大小顺序。本文的相关研究结果可帮助工程人员进一步了解定点返回轨道的相关特性,同时也可为进一步的定点返回轨道的优化设计提供参考。

1 问题描述

对于定点返回轨道,还需要同时满足工程约束和轨道约束,其中月地返回轨道的终端特征点如图1所示, 图中A为返回轨道升交点,R为再入点,V为真空近地点,I为月球反垂点,S为着陆点。

图1 月地返回轨道终端特征点

轨道约束主要包括出发环月轨道约束、地球终端约束和返回窗口约束,环月轨道约束主要为环月轨道高度约束。

(1)

(2)

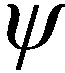
(3)

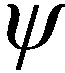
(4)

地球终端约束需要满足着陆点位置要求:

(5)

(6)

2 基于可控域的全局参数敏感性分析方法

2.1 可控域计算模型

可达域通常指在如式(7)的动力学系统中,t∈[t0,tf]系统连续,给定t0时刻初始状态x(t0)∈Θn,存在控制量u(t)=Um,使得tf时刻终端状态x(tf)∈Πn,则称集合Πn为初始状态集合Θn对应的可达域。

(7)

式中:(·)为对时间进行微分;y(t)为t时刻的状态。在有些情况下,终端状态可达域并不直观,也不是所有参数都需要关注,转而求解对应的可达域Yk。在本文所研究的定点返回轨道,其可控域是在给定返回轨道终端约束的情况下,由初始时刻的近月点轨道参数组成的多维参数集,实际上是上述可达域问题的逆问题。飞行器在tf时刻的约束为

(8)

则飞行器在t0时刻的参数可控域可以用一般化的数学描述为

(9)

在实际中对定点返回轨道进行分析设计时,主要关注近月点的设计参数在初始时刻的分布范围,其对应的可控域可以表示为

(10)

在可控域计算中,首先给定返回时刻以及约束条件,然后对返回窗口进行判断,若当前时刻满足定点返回轨道窗口约束,则遍历近月点伪参数,通过圆锥曲线拼接法对定点返回轨道进行求解,得到转移轨道的终端参数,然后判断该轨道是否满足当前时刻的约束条件,若满足定点返回轨道要求,则输出近月点参数以及对应的转移轨道参数,若不满足则选择下一组近月点参数进行计算,直至近月点参数遍历完成。计算可控域的流程图如图2所示。

图2 可控域计算流程图

2.2 全局参数敏感性计算方法

对于本文的定点返回轨道问题,可将计算模型在数学上描述为一个函数映射:

Y=Y(X1,X2,…,Xd)=Y(X)

(11)

式中:X=[X1,X2,…,Xd]为用向量表示的模型输入参数;d为输入参数数目;Y为模型的输出参数,可表示为

Y=[Y1,Y2,…,Ym]

(12)

式中:m为输出参数的数目。在文本研究的定点返回轨道问题中,X为近月点伪参数,Y则为转移轨道的终端参数。目前,常用的敏感性分析方法通常分为局部敏感性分析方法[30]和全局敏感性分析方法[31],对于本文所研究的可控域敏感性问题,局部敏感性只能反映局部点处的敏感性信息,无法在区域范围内对各参数的敏感性进行综合分析。因此,需要使用全局敏感性分析方法对可控域内的参数集合点进行敏感性分析。

Saltelli在基于方差的全局敏感性分析基础上提出了一种蒙特卡罗计算方法[32],该方法只需要对样本点进行单层抽样,假设采样次数为N,参数数目为d。该方法首先在参数空间范围内进行采样生成两个初始分析矩阵A和B,然后通过矩阵间的变换总计得到N+2d个计算输入矩阵,再将上述矩阵代入到蒙特卡罗计算公式中,可得到各参数的敏感性结果。但通常计算得到的定点返回轨道的可控域结果为限制在空间某一范围中的结果,若采用上述方法在整个空间范围内进行采样会产生很多非可控域内的参数集合点。以三参数的可控域范围为例,如图3(a)所示,可以看出在使用采样方法采样时,会在空间立方体中生成一系列采样点。该立方体中除了可控域集合中的状态点,还包含了许多非可控域内的状态点,在敏感性计算中仍使用空间中生成的序列采样点进行计算会对结果产生较大的误差。由于在计算可控域的过程中已经计算出一组参数集合点,该集合点在该区域内为近似均匀分布,同时在计算定点返回轨道中的等式约束一般是限制在允许的误差范围内,在可控域集合点附近加上微小扰动仍存在满足定点返回轨道要求的集合点。因此,可以在原有的可控域集合点施加小扰动变量生成另一组可控域集合点,如图3(b)所示。这样将这两组可控域集合点作为初始分析矩阵进行全局敏感性分析得到的结果仍然是限制在可控域范围内的敏感性结果,可以较为准确的反映在可行解范围内参数的敏感性。

图3 空间采样点与可控域集合点关系图

基于上述考虑,针对定点返回轨道的可控域问题,结合Saltelli的蒙特卡罗方法,提出一种基于可控域的全局敏感性分析方法,该方法的基本计算步骤如下。

(1) 首先通过模型计算得到满足要求的近月点参数可控域集合A:

(13)

(14)

(15)

(3) 将上述d+2个样本矩阵代入计算模型中,可得到d+2个输出矩阵:

(16)

式中:A(j)(j=1,2,…,N)表示矩阵A的第j行,其余各项定义类似。

(4) 选择输出参数Yl(l=1,2,…,m),将上述结果代入到蒙特卡罗计算公式中计算各阶方差:

(17)

(18)

(19)

式中:YA(l)表示矩阵YA中对应Yl的输出结果向量;X～i表示除了参数Xi之外的其他参数;X～ij表示除了Xi和Xj之外的其他参数。总方差为

(20)

然后通过敏感性指标可以计算出各阶敏感性系数:

(21)

(22)

(23)

式中:V(·)表示方差;E(·)表示期望;Si为一阶敏感性指数,表示单一模型参数对模型输出的影响;Sij为二阶敏感性指数,表示两个模型参数的组合对模型输出的影响;STi为全局敏感性指数,表征的是所有包括第i个模型参数在内的参数组合对于模型输出的影响。上述敏感性系数在计算时基于已有的可控域集合点,不需要进行额外的采样点生成,因此敏感性结果可以较为准确的反映在定点返回轨道可行解范围内各参数之间的敏感性信息。

3 仿真分析

3.1 可控域计算

在仿真分析中,为统计不同返回时刻下的定点返回轨道可控域分布的一般规律,分别选取近月点时刻为T1: 2029-2-10 08:53:12.522 37、T2: 2029-5-2 01:34:52.328 033、T3: 2029-08-21 22:44:19.936 099,着陆场位置为(100°E,41°N),近月点高度为100 km,返回再入角-6°,返回时间不超过3.5天,返回轨道采用降轨出发,升轨到达方式。在计算中遍历近月点伪经纬度,最终计算得到的可控域结果。为验证本文方法计算得到的可控域的准确性,首先选择T1时刻,然后将本文计算得到的可控域与采用多圆锥截线法[26]计算得到的可控域进行对比,结果如图4所示。

图4 不同计算方法得到的可控域范围

图4中,图4(a)为两个可控域范围的对比图,图4(b)表示由多圆锥截线法计算得到的可控域范围,图4(c)表示由圆锥曲线拼接法得到的可控域范围。从两个图的比较分析中可以看出,由两种方法计算得到的可控域范围基本一致,本文的计算方法可较为准确地反映定点返回轨道的可控域范围,因此继续采用本文方法进行后续的计算。进一步比较不同时刻下定点返回轨道的可控域分布范围,结果如图5所示。

图5 近月点伪经纬度可控域

从图5中结果可以看出,对于不同返回时刻下的定点返回轨道,满足定点返回条件的近月点伪经纬度可控域分布均较为连续,且可控域分布的范围和形状均比较相似,伪经度范围约在-30°～40°,伪纬度范围在-50°～30°。由于不同定点返回轨道间近月点参数可控域的相似性,因此在本文后续的分析中,只选取时刻T1下的定点返回轨道进行分析。

图6所示为T1时刻下近月点偏心率和速度倾角与近月点伪经纬度间的关系。从图6可以看出,T1时刻下的定点返回轨道的伪参数近似分布在一连续的区域范围内,具体分布范围如表1所示。表1中,αmin表示参数区间范围下限,αmax表示参数区间范围上限,Δα为参数区间范围。偏心率和倾角的范围均和伪经纬度的位置有关,偏心率的大小分布在1.3～2,且偏心率的大小大致随着近月点伪经度的增加而减小。近月点速度倾角的范围分布在160°～240°,与偏心率不同,速度倾角的大小受近月点伪纬度的影响较大,其大小近似随着伪纬度的增加而减小。

表1 近月点参数可控域区间范围

图6 近月点偏心率与速度倾角范围

3.2 参数敏感性分析

由上述可控域分析已知在给定约束条件下的定点返回轨道伪参数的可控域范围区间,为进一步判断近月点参数对定点返回轨道终端参数具体的影响程度,在此基础上使用本文提出的基于可控域的参数敏感性分析方法对定点返回轨道的参数进行敏感性分析。

在参数敏感性分析中,输入参数为4个伪参数设计变量,输出参数选择工程中的主要关注参数,分别为再入点经度、再入点纬度、返回时间、返回轨道倾角以及真空近地点高度。在进行参数敏感性分析前,首先进行误差收敛性判断以确定k的取值大小。不同的k值下,计算得到再入点经度误差限的结果如图7所示,本文收敛误差限取值为2°,图中所示结果即为计算得到的约束误差除以收敛误差限后的结果,当误差限小于1即认为满足约束要求。从图中可以看出,当k值取值较大时,有较多的集合点不满足约束参数的收敛要求,随着k取值的减小,落在误差限内的集合点数目逐渐增加。进一步统计满足定点返回轨道所有约束的集合点个数,如图8所示,当k=10-7时,满足约束的集合点个数为2 813(集合点总数为2 839),达到了99.1%,此时可认为矩阵B中的集合点已基本满足定点返回轨道约束要求。

图7 不同k值下集合点收敛情况

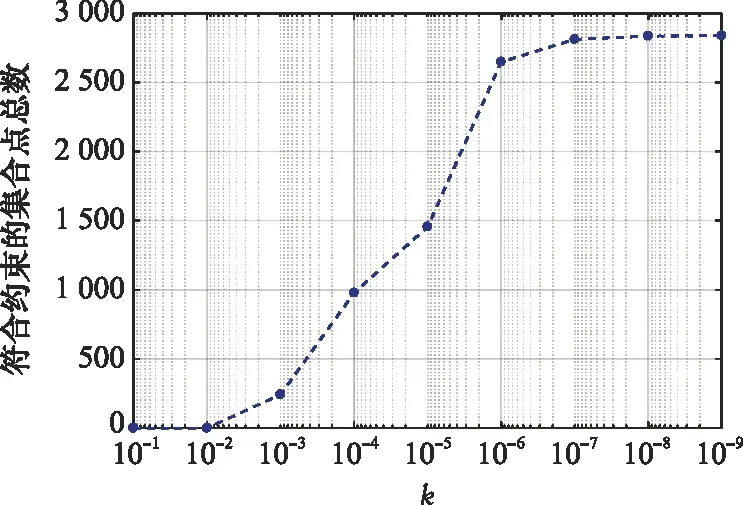
图8 符合约束要求的集合点总数随k值变化情况

进一步分析在不同k值下参数敏感性分析结果的变化情况,如图9所示。图9中结果为近月点经度对再入点经度的敏感性结果,从图中可以看出,当k取值较大时,参数敏感性计算结果不稳定,出现较大的变化幅度。而随着k取值减小,参数敏感性的计算结果逐渐稳定,当k取值为10-7时,参数敏感性计算结果为0.223 225,相比于k取值为10-9的计算结果0.223 240 25变化幅度仅为0.030 6%,当k值小于10-7时,k的取值对参数敏感性结果影响很小,因此在本文中取k=10-7进行后续的分析计算。

图9 不同k值下的敏感性系数结果

近月点伪参数的可控域范围通过上述计算已知,然后在计算得到的伪参数可控域矩阵A基础上通过比例因子k生成矩阵B,接着通过上述两个矩阵进行参数敏感性分析可得到近月点参数对转移轨道终端参数的敏感性指标。由于在可控域范围内,每个可行状态点的变化往往伴随着多个参数的改变,需要考虑各参数在整个可控域内与各参数相互作用下对结果的综合影响,因此主要统计各参数的全局敏感性系数即STi,得到的结果如图10所示。

图10 全局参数敏感性分析结果柱状图

从图10的敏感性分析结果可以看出,通过敏感性分析可以具体地区别出各参数对输出结果的敏感性大小,从而判断不同参数间的影响程度。对于不同的输出参数,近月点参数的敏感性大小也各不相同,具体敏感性结果如表2所示。从表2中可以看出,对于所选的输出参数来说,近月点偏心率均为最敏感的参数,说明在4个伪参数设计变量中偏心率对定点返回轨道的转移终端参数最为敏感,因此在对定点返回轨道进行进一步优化和调整时需要主要考虑偏心率对结果的影响。此外,从表2中也可以看出,在输出参数的低敏感性参数中,除返回轨道倾角的低敏感性参数为近月点速度倾角外,其余参数的低敏感性参数均为近月点伪纬度。因此,从整体上看近月点伪纬度对定点返回轨道的终端参数影响较低,在对定点返回轨道进行进一步优化和调整时可降低对近月点伪纬度调整的优先级。

表2 参数敏感性排序

4 结 论

本文针对月球探测任务中的定点返回轨道,对给定约束条件下的近月点参数可控域进行了分析,并在此基础上提出了一种基于可控域的参数敏感性分析方法。在可控域分析中,给出了不同时刻下的定点返回轨道的近月点参数可控域范围,以此给出了定点返回轨道可控域分布范围的一般规律。在计算得到近月点参数可控域的基础上,具体分析了在定点返回轨道可行解范围内的近月点参数对轨道终端参数的影响程度,给出了参数的全局敏感性指标以及参数间组合的敏感性指标。在实际的轨道设计任务中,可根据求得的参数敏感性结果,对于高敏感性参数需要精确求解范围或者提高权重比,对于低敏感性参数则可缩小其搜索范围或者固定为常量。同时,上述结果为二体条件下的计算结果,因此相关敏感性分析可作为进一步高精度求解的初始判断条件,从而提高求解效率。本文的相关研究结果可为未来的载人月球探测任务提供重要参考。