基于迎角分区的全局飞行器气动参数辨识方法

臧剑文, 毕晓烨, 金 钊, 刘 浩, 闫 明

(1. 大连理工大学航空航天学院, 辽宁 大连 116024; 2. 沈阳飞机设计研究所, 辽宁 沈阳 110035)

0 引 言

近年来,随着系统辨识理论的研究,飞行器气动参数辨识在飞行试验中的应用得到了飞跃发展,并在飞行器设计中起着越来越重要的作用,采用参数辨识方法来确定飞机参数,能够准确并迅速地将真实气动特性从试验结果中分离出来,对缩短数据处理时间和减少飞行试验周期等具有重要应用价值[1]。

在大迎角机动时,由于机身机翼表面的气流经历了附着流-旋涡流-涡破裂的历程,这才使得飞机气动特性呈现强非线性等特征。传统的线性辨识方法对大迎角机动非线性气动参数辨识精度较低,因此线性辨识模型不适用于大迎角机动情况。

张家铭等[2-3]提出了基于机器学习的气动参数辨识方法,但该方法需要足够多的数据样本,不适用于在线辨识。李正强等[4]提出基于最小二乘支持向量机(least squares support vector machines,LS-SVM)飞机大迎角动态辨识方法,该方法的弊端在于LS-SVM模型的学习时间较长,支持向量机的速度较慢,不适用于在线辨识。乔伟等[5-6]提出基于递推最小二乘法的飞行器模型参数在线辨识,但弊端在于无法直接用于非线性复杂运动过程。苏振宇[7-8]提出基于试飞数据的飞机大迎角气动力参数辨识方法,但弊端在于人为将迎角分割为若干小区间,不具备自动分区的能力。张婉鑫等[9]提出大迎角非定常气动参数辨识方法,该方法在数据处理的过程中要求通过插值法求解二阶导数、三阶导数等,数据存在较大的误差。

飞机大幅度机动飞行时,气动特性表现出非线性特征,特别是当飞机具有高迎角姿态时,数据愈加离散,传统的辨识方法拟合效果较差[10]。本文基于“局部线性化”的思想,提出大迎角数据实时自动分区的辨识方法,将大范围的迎角数据自动划分为几个小范围的子区域,将一个复杂的非线性建模问题分解为若干个局部线性问题,进而辨识每个子区域内的气动参数。该方法与传统的参数辨识方法相比,辨识模型结构相对简单,且适用于非线性复杂运动等情况[11];与深度学习的方法相比,不需大量的数据样本进行神经网络的训练,可应用于在线辨识[12];与插值法求解高阶导数的方法相比,数据精度较高,有利于提高后续的辨识精度[13]。

1 飞行器参数辨识模型

在参数辨识之前需要建立辨识模型,由于飞行器参数之间存在强耦合,导致辨识难度大。本文将飞行器的运动分解为纵向运动和横侧向运动,以纵向运动模型中俯仰力矩系数、升阻力系数为例,建立动力学参数辨识模型[14]。

1.1 纵向运动模型

把飞行器运动分解为纵向运动和横侧向运动,并以两组相互独立的运动方程组来描述[15]。通过对飞行器纵向受力进行分析,得到如下微分方程组[16]:

(1)

式中:m为飞行器质量;P为发动机推力;X为空气阻力;Y为升力;ωz、Mz为俯仰角速率、俯仰力矩;x、y为x轴、y轴方向上的位移;Jz为转动惯量;α、ϑ、θ为迎角、俯仰角和轨迹倾角。

1.2 观测模型

在真实的飞行过程中,升阻力系数、俯仰力矩系数不能通过传感器直接测得,而是根据其他可观测的参数计算得到,由此需要建立可观测参数与力矩系数的观测模型,为后续的辨识过程提供待辨识参数的观测值[17]。

(2)

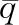
(3)

空气动力学的整体模型的理想形式是同时具有估测的模型参数值和相关不确定性的数学模型结构,可以将无量纲的空气动力学中的力和力矩系数与可以测量的飞机状态和控制联系起来。所有的全局辨识都是基于时域的方程误差最小二乘法来进行建模。在此方法中,因变量是无量纲力或力矩系数中的某一项,它是通过利用解释变量(无量纲的飞机状态量和控制面挠度)计算出非线性模型项的扩展来进行建模的[18]。

因此,可以使用特定模型结构来表达俯仰力矩系数的方程误差最小二乘问题。设置建模函数如下:

(4)

式(4)可以写成:

z=Hθ+v

(5)

其中,z代表观测模型计算的观测值:

(6)

H代表设置的建模函数:

(7)

θ代表辨识模型:

(8)

v代表残差:

(9)

2 动力学参数辨识方法

2.1 基于轴正交决策树的迎角自动分区

回归树是一种具有逻辑性的分类方法,可以为局部建模网络划分权重变量,并分出新的单元结构,该过程将解释变量归入不同的区域,来表征解释变量的非线性特征。分区方法通常采用二进制拆分法则,图1所示二进制轴正交决策树网络结构,在具有两个权重变量的情况下,在每个级别的单元格中再拆分出一个新单元格。被划分的单元称为母单元,随后拆分出的单元称为子单元[19]。

图1 二进制轴正交决策树网络图

一个回归树对应着对输入空间的一个划分,以及在划分的单元上的输出值。假设把输入空间划分为M个互不相交的单元R1,R2,…,RM,且在每个单元Rm上都有固定的输出值Cm(m=1,2,…,M),则回归树模型[20]可表示为

(10)

可迭代的二进制轴正交回归树算法已成功用于各种非线性静态和动态建模应用程序中。

假设:

(11)

对于任意的t,总要消除y(t)对其中一个xi(t)的依赖性,比如xi(t)取xp(t)。通过分区,可以在{x1(t)x2(t) …xn(t)}的真子集上重新定义y(t)[21]为

(12)

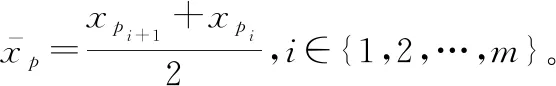
2.2 飞行器在线辨识激励信号设计

实时气动建模时需要迅速地收集到所有刚体自由度的数据信息,而在一系列飞行条件下,将自动正交优化的多正弦扰动施加在控制舵面上可以很有效地收集相关气动数据[23]。使用扰动输入来激励飞行过程,该输入通过将设计好的激励信号与控制指令中的执行器命令相加,以此作为飞行器的舵面指令。

设定应用在第j个控制面的扰动输入为uj,其为具有单个相移的正弦波谐波φk的总和[24]。

(13)

式中:M是可用的谐波相关频率的总数;T是激励的时间长度;Ak是正弦波分量的振幅;t是时间分量;nj个输入中的每一个都是从M个谐波正弦波中选择具有频率ωk=2πk/T的分量,k=1,2,…,M。ωm=2πM/T代表激励输入的频带上限。区间[ω1-ωm]代表了指定期望飞机动力学的频率范围。

为了实现均匀的功率分配,Ak被设置为

(14)

式中:n是包含在等式(13)中的正弦分量的数量;A是输入的uj幅度。

2.3 时域递推最小二乘辨识方法

使用递推最小二乘法进行参数辨识时,首先要利用已知观测量和输出量计算递推初值。在已知k时刻之前所有的观测和输出时,记B(k)=HT(k)H(k),则前k时刻所计算的递推初值为

θ(k)=B(-1)(k)HT(k)z(k)

(15)

在实际使用的过程中,随着信息的增加,信息矩阵的正定性不断减小,对新的信息改进作用逐步等于零,这一现象称为数据饱和现象[25]。为解决这一问题,提出了引入遗忘因子的递推算法。递推公式[26]如下:

(16)

经式(16)递推计算得到θ4×N矩阵:

(17)

z=Hθ4×N

(18)

由式(18)可知:

(19)

2.4 基于加权函数的数据平滑方法

当每个局部模型辨识气动参数以后,需要对全局范围内气动参数进行数据平滑整合,该部分基于加权函数对局部模型的临界数据进行数据平滑[27]。具体步骤如下:

(1) 对第k个区域进行有效性分析:根据之前确定的权重变量,φ=[φ1,φ2,…,φnφ]利用下式计算该区域的有效性:

(20)

Ck,j是第j个权重变量在该单元格内的中心点的高斯函数,计算公式如下[28]:

(21)

式中:μ代表在该单元内的该分区变量的均值;σ2代表方差。值得注意的是,由于权重变量是随着数据点的不同而不断变化的,而在每段区域中心处求该区域中心点的高斯中心值是固定的,因此根据上述公式得当某点离某一区域的高斯中心越远时,该区域在这点处有效性越小[29]。所以,比如对第一个区域内的某一数据点来说,主要是第一个区域在该点有效性比较大,离其他区域越远,则其在该点有效性越小。

(2) 根据上述公式得到各个区域的有效性后,通过式(22)来计算第k个单元的权重[30]。

(22)

(3) 利用计算出的各个单元格的权重,进行全局平滑建模。对每个点的整体建模,采用各个单元内区域建模的加权加和得到[31]:

(23)

首先,平滑的依据有两个:① 在断点处的值相等;② 在断点处导数相等。

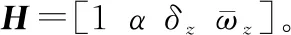
(24)

则在临界点的平滑计算值为

(25)

证毕

以上平滑的两点依据均满足,因此可以认为该曲线已经平滑。通过上述过程,可以将各个分区的建模结果进行平滑加权加和,从而得到一个平滑后的有效的整体模型。

3 仿真实例

为验证本文方法的有效性,针对飞行高度7 500 m、Ma0.4的某飞行器飞行数据,建立纵向运动模型、辨识观测模型以及递推最小二乘辨识模型,总仿真时间为ts=25 s,仿真步长为tk=0.01 s。飞行器的相关参数如表1所示。飞行器的飞行状态数据如图2所示。

表1 飞行器相关参数

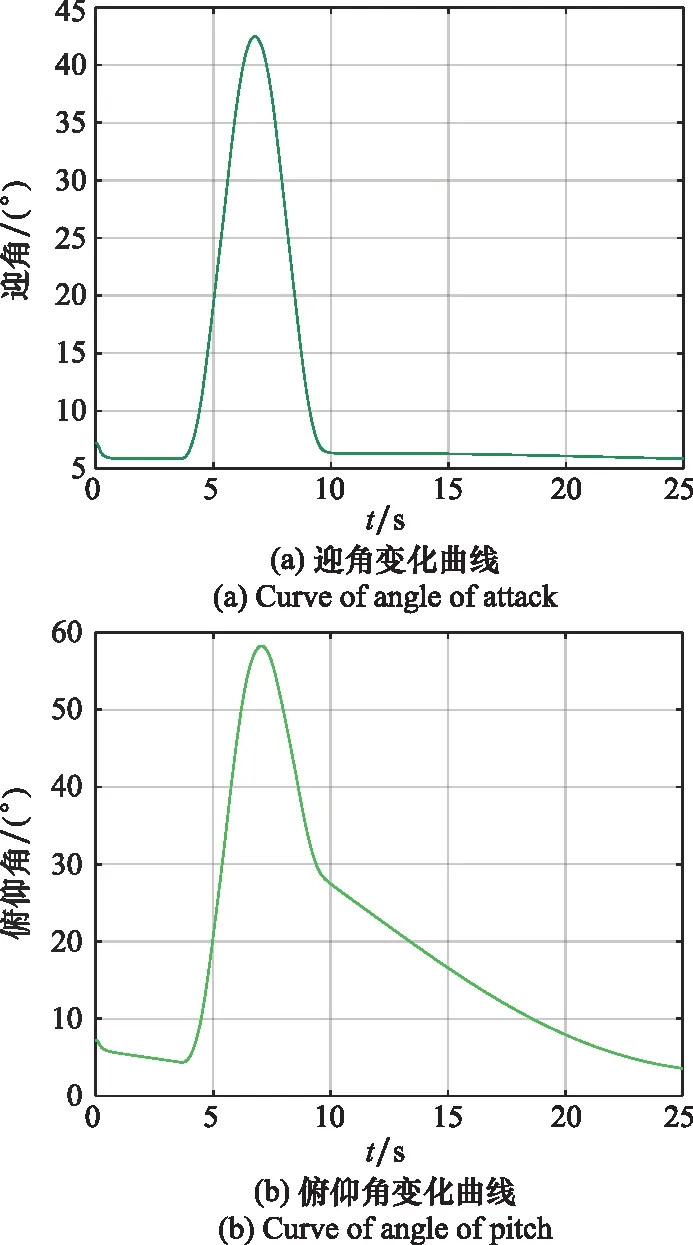
图2 大迎角机动仿真数据

3.1 仿真计算结果及分析

图3展示仿真流程示意图,仿真流程主要包括3个方面:基于激励信号的数据收集,建立观测模型、空气动力学模型、最小二乘辨识模型,基于加权函数的数据平滑处理。

图3 仿真流程示意图

本文将激励信号设计为具有特定谐波频率,优化相移和指定功率分布之后的正弦波之和[32],如图4所示。

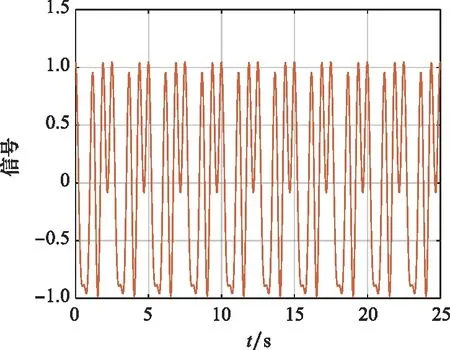
图4 正弦激励信号

公式表达如式(26),其中T=5 s。

(26)

选择特定的分量频率以覆盖飞行器姿态运动包含的频带[33]。另外,将激励信号设计为多元输入,保证其在时域和频域中相互正交,以使其在短时间内所有轴上都具有较高的数据信息含量[34]。

在充分获取数据的基础上,建立俯仰力矩系数、升力系数的观测模型如式(27)。取迎角变化范围为5°,基于回归树迎角自动分区结果如图5所示。

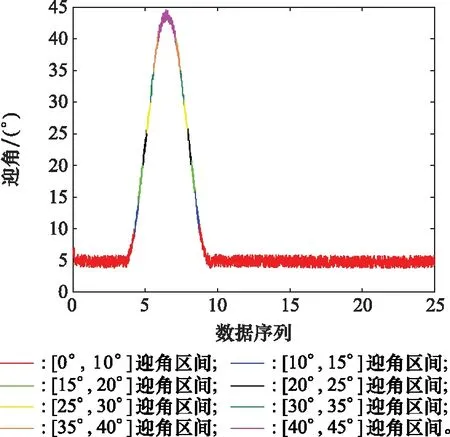
图5 回归树迎角自动分区结果

(27)

根据每个分区的辨识情况,总结了计算俯仰力矩系数、升力系数各项参数的辨识结果。由图6和图7可知,气动导数在5 s左右已经收敛,且收敛速度较快。气动导数的辨识精度分别为2.1%、2.9%、1.6%,详见表2。

表2 俯仰力矩系数辨识精度

图6 俯仰静稳定系数和升降舵效率辨识结果

由图8和图9可见,升力系数的气动导数辨识收敛较快,辨识精度分别为0.6%、0.5%,详见表3。

表3 升力系数辨识精度

图8 迎角系数和升降舵系数辨识结果

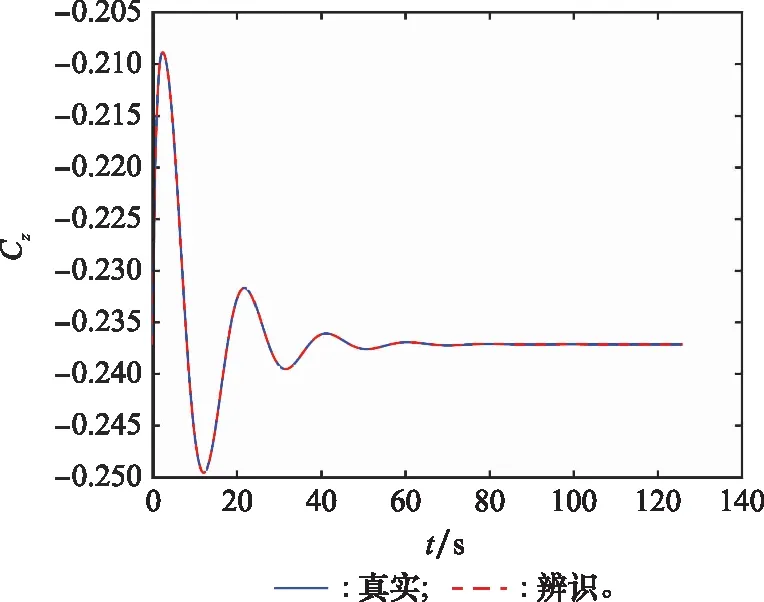
图9 升力系数辨识结果

为充分证明迎角分区时域辨识精度较传统全局辨识精度高,下文阐述迎角分区与传统全局的辨识结果对比,如图10所示。

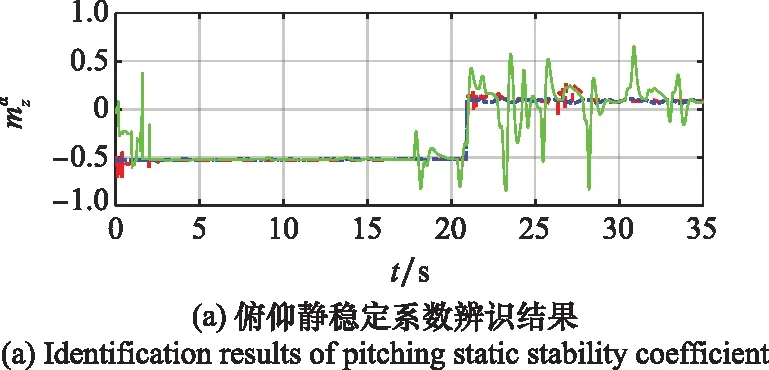
图10 俯仰静稳定系数和升降舵效率辨识结果

由表4可知,利用迎角分区辨识的方法,辨识俯仰静稳定系数、升降舵操纵效率以及俯仰阻尼力矩系数,其相对误差均在3%以内。与传统全局辨识结果相比,待辨识参数的平均相对误差明显降低,精度更高。

表4 不同辨识方法误差对比

3.2 不同迎角区间长度的离线辨识时间对比

为研究分区数量与辨识时间的关系,本文分别进行5°迎角区间、3°迎角区间、2°迎角区间以及传统全局不分区仿真实验,记录辨识时间如表5所示。

表5 不同迎角区间长度的离线辨识时间

根据表5能得到如下结论:迎角区间越小,分区的数量越多,离线辨识的时间越短。由此有以下建议:若迎角数据充分且对精度要求不高,可以适量减小迎角区间长度,增大分区的数量,由此可减小程序运行时间,提高计算效率。

4 结 论

本文基于递推最小二乘法,围绕局部线化代替整体非线性的思想,采用按回归树迎角分区的方法,对飞行器动力学模型中未知参数的时域辨识方法进行了研究。

首先,根据飞行器的纵向动力学方程,建立了适用于仿真验证的观测模型。之后,根据时域局部平滑法得到观测模型所需要的观测数据。在此基础上,按照迎角分区方法,将所得数据划分多个区域,区域间是相互独立的,且能够连续更新。并在每个不同的区域内采用递推最小二乘法,分别进行时域辨识。最后,将每个区域的辨识结果利用加权函数整合,重构俯仰力矩系数。

仿真过程和结果表明,本文基于递推最小二乘法的时域分区辨识方法,可以较为准确地给出局部气动参数的估计值,具有辨识精度高、计算效率高的特点,且所有的参数辨识误差小于3%,有利于了解全局气动模型中的局部气动特性。另外,通过比较不同迎角区间长度,得到“可适量减小迎角区间长度,增大分区数量,提高计算效率”的结论。然而,如果各区间迎角变化范围取值较小,容易导致各区间仿真数据缺少足够用于辨识的有效信息。进而递推初值计算误差大,影响辨识精度,具有一定的局限性。因此,需要提供大量且充分激励的仿真数据。