基于非标准Keystone变换的波形捷变雷达相参积累算法

张 亮, 陈 辉, 张昭建, 王晓戈, 王永良,*

(1. 空军预警学院预警技术系, 湖北 武汉 430019; 2. 中国人民解放军94326部队, 山东 济南 250000)

0 引 言

雷达作为现代武器系统的重要组成部分,为应对复杂电磁环境下的有源干扰威胁,需要具备较强的反侦察、抗干扰能力。为取得对抗优势[1],雷达系统抗干扰设计需要解决两个问题:一是如何避免干扰信号进入雷达系统;二是干扰信号已进入雷达,如何剔除干扰。对于第一个问题,通常采取参数捷变的方法,增大干扰机对雷达参数的侦收难度,降低干扰信号进入雷达系统概率;对于第二个问题,主要利用目标回波与干扰信号特征差异,空、时、频域抑制干扰信号。雷达典型参数捷变措施包括频率捷变、重频捷变、波形捷变等[2]。但受雷达天线架构、信号处理、指标要求等诸多限制,雷达载频、重频捷变范围通常较为有限。而近年来对雷达波形捷变的优化设计[3-4]成为一个重要的研究方向,较好地解决了雷达反工作模式侦察[5]、抗主瓣干扰[6-7]、距离旁瓣抑制[8]、射频隐身[9]、改善跟踪精度[10]等诸多难题,同时衍生出多输入多输出(multiple input multiple output, MIMO)雷达[11]、波形分集阵列雷达[12]、认知雷达[13]等新体制。雷达波形捷变虽然是一种有效的干扰对抗方法,但具体应用中需要解决波形捷变与雷达体制兼容性问题,其中以波形捷变相参积累最为关键。针对该问题,文献[14]设计了一种随机初始相位调频斜率捷变线性调频(linear frequency modulation, LFM)波形,用以对抗距离假目标干扰,但文献[14]未明确捷变波形时宽与带宽,而这些参数与相参处理关系密切。文献[15]提出利用变脉宽调频斜率捷变LFM波形,对抗针对合成孔径雷达的欺骗干扰,然后脉宽的变化会影响脉压后的目标峰值,成像效果不理想。针对该问题,文献[16]设计了一种变带宽调频斜率捷变LFM,该波形不存在上述问题,但由于波形脉宽固定,反侦察效果不佳。上述研究的侧重点是干扰抑制,对波形的低截获、相参性研究还不够深入,另外,目标高速运动容易出现跨距离门问题,文中同样未考虑。Keystone变换(Keystone transform, KT)是一种常用的雷达目标距离走动校正方法[17],标准的KT包含两个核心环节,即模糊数补偿和慢时间的时间尺度(time-scaling, TS)[18],由于需要搜索目标速度模糊数,搜索区间的扩大会导致计算量成倍增加,因此亟待寻求一种无需模糊数补偿的KT实现方法。

针对上述问题,提出基于非标准KT的波形捷变雷达相参积累算法。首先,对脉压后回波沿快时间进行傅里叶变换;其次,计算非零频(快时间频率)慢时间回波与零频慢时间回波尺度互相关函数,估计对应的尺度因子;再次,沿慢时间对回波进行TS,其中的尺度因子由前面估计的尺度因子取倒数得到;然后,对TS后的回波沿快时间进行傅里叶逆变换,完成目标距离走动校正;最后,对目标距离走动校正后的回波沿慢时间进行傅里叶变换,实现相参积累。另外,利用TS操作,设计了一种脉宽、带宽同时捷变低截获LFM波形,该波形不仅与相参体制雷达具有较好的兼容性,还可以实现目标距离不展宽旁瓣抑制。

1 雷达脉间捷变波形

雷达捷变波形有多种,设雷达发射基准波形为x(t),本文利用TS设计脉间捷变波形,即

(1)

式中:y(t)为脉间捷变波形;TSα[·]为TS表示符号;α∈R+为尺度因子(scale ratio, SR),不同的α对应不同波形。设x(t)、y(t)的傅里叶变换分别为X(f)、Y(f),根据傅里叶变换尺度特性可知

(2)

雷达波形设计中通常基于实际的应用需求确定,常用波形主要包括线性调频、非LFM(non-LFM, NLFM)以及相位编码信号等。设基准波形为LFM脉冲信号,可表示为

(3)

式中:T为脉宽;k=B/T为调频斜率;B为带宽。当TB≫1时,s1(t)频谱可近似为

(4)

设雷达捷变波形s2(t)=TSα[s1(t)],即

(5)

根据式(2)可知:

(6)

易知s2(t)带宽为aB,很明显,为满足采样定理,上述波形设计中应确保α取值介于0到fs/B之间,fs为采样频率。分析捷变波形s2(t)经雷达匹配滤波输出结果,首先以s2(t)为匹配信号,对s2(t)进行频域匹配滤波,容易得到匹配输出信号为

(7)

式中:F-1[·]为逆快速傅里叶变换(inverse fast Fourier transform, IFFT)表示符号。可以看出,s2(t)匹配输出信号近似为辛格函数,第1级零点宽度为2/(αB),峰值均为T,与尺度因子α无关,说明该波形具有固定压缩比特点,即脉压后目标峰值相同,便于后续的相参积累。下面再以s1(t)为匹配信号对s2(t)进行匹配滤波,当α>1时,可得

(8)

式(8)近似为LFM信号,时宽约为T(α2-1)/α2。同理,当α<1时,可得

(9)

式(9)时宽约为T(1-α2)/α。可以看出,该捷变LFM波形非完全的正交信号,不适用于正交波形应用场景,下节将介绍该波形捷变条件下的雷达相参积累原理。

2 波形捷变雷达相参积累原理

设雷达发射式(5)脉间捷变LFM波形,雷达接收射频回波经下变频处理,目标回波基带信号可表示为

sr(t,tm)=σs2[t-2R(tm)/c]exp(-i4πf0R(tm)/c)

(10)

式中:t为快时间;tm为慢时间;σ为反射系数;R(tm)=R0-vttm为目标与雷达径向距离函数;R0为目标初始距离;vt为径向速度;c为光速;f0为载频。设相参积累个数为M,脉冲重复间隔(pulse repetition interval, PRI)为Tr,对于固定PRI,慢时间可表示成离散形式,即tm=mTr(m=0,1,…,M-1)。对式(10)进行脉冲压缩,忽略反射系数σ,结合式(7)可得脉压后的回波为

ys(t,tm)=

(11)

当vt(M-1)Tr大于雷达1个距离单元时,目标出现距离走动,与雷达波形不捷变时情况相同。类似于捷变频雷达中的频率调制码字,式(11)中包含一个由雷达方设定与慢时间有关的变量α,下文记为α(tm)。设快时间频率为f,目标不模糊多普勒频率为fd,速度模糊数F,脉冲重复频率为fr,fr=1/Tr,频域尺度因子为αf,αf=(f+f0)/f0,下面分析标准KT能否适用波形捷变雷达目标距离走动校正。将式(11)模型应用于标准KT的步骤如下。

步骤 1对脉压后回波沿快时间做傅里叶变换,得到

ys(f,tm)=exp(i2π[αf(fd+Ffr)]tm)·

(12)

步骤 2对ys(f,tm)沿慢时间进行模糊数补偿,得到

(13)

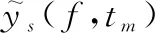
(14)

对于窄带雷达,频域尺度因子αf介于1附近,式(14)可近似表示为

(15)

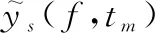
(16)

可以看出,校正后的目标峰值位置相同,对式(16)进行快速傅里叶变换(fast Fourier transform, FFT)不影响目标的正常积累。步骤3中TS操作改变了信号时宽,为确保TS前后回波慢时间采样点数相同,需对TS后回波时域补零(αf<1)或者截取(αf>1),为直观显示,图1给出了回波截取补零示意图(横坐标为快时间频率,纵坐标为慢时间),图中红色区域为时域待截取回波部分,绿色区域为补零部分,最左侧图之所以为梯形是因为式(5)雷达捷变波形带宽随尺度因子而变化(图中假设波形带宽为线性变化)。

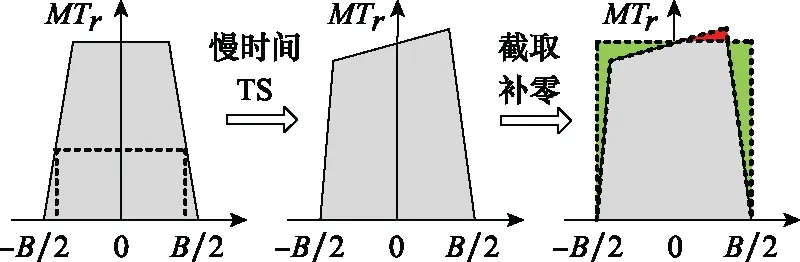
图1 回波截取补零示意图

上述分析可知,标准KT能够适用波形捷变雷达目标距离走动校正,再利用FFT可实现相参积累。标准KT存在一个固有的缺点,即需要估计目标真实模糊数,对于该问题,现有方法是设定模糊数区间,根据相参积累后的目标最大峰值搜索确定,搜索区间的扩大会导致算法运算量成倍增加。针对该问题,本文提出一种无需模糊数补偿的KT实现方法,在介绍所提方法前,首先引入一个基本概念,即尺度估计(scale-estimation, SE)。设连续信号u(t)=TSα1[v(t)],α1>0。所谓SE,即u(t)、v(t)均已知时对α1的估计。为估计α1,需计算u(t)、v(t)的尺度互相关函数(scale cross correlation function, SCCF):

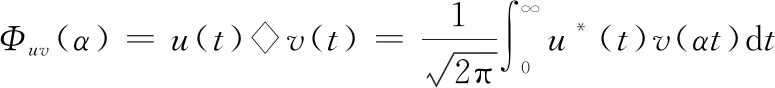
(17)

(18)

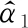
x(f,tm)=exp{i2π[αf(fd+Ffr)]tm}

(19)

进一步表示为

(20)

(21)

(22)

(23)

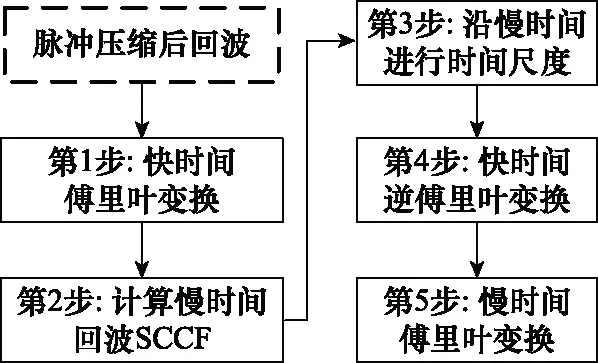
图2 波形捷变雷达相参积累流程

3 基于梅林变换的尺度估计方法

所提非标准KT具体实现上有两个问题需要解决:一是如何计算回波SCCF;二是如何对慢时间回波进行TS处理;对于第一个问题,本文利用梅林变换(Mellin transform, MT)解决SCCF数值计算问题,对于第二个问题,同样可利用MT实现,也可以使用辛格插值、Chirp滤波、尺度傅里叶变换等方法[16],不做详述。

3.1 MT与尺度变换

MT是一种积分变换,在舰船及语音信号识别、尺度滤波、尺度不变系统设计、图像配准、超声波温度补偿等领域应用广泛[19-20]。连续信号f(t)的MT定义为

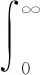
(24)

式中:z=η+iμ为MT复自变量。MT最重要的性质为尺度不变性(与傅里叶变换时移不变性相对应),设连续信号h(t)=TSα[f(t)],其MT为

(25)

易知,当η=0.5时,|Mh(z)|=|Mf(z)|,TS前信号与TS后信号的MT包络相同、相位不同,此时MT也称为尺度变换(scale transform, ST)。以此为基础,文献[18]进一步提出尺度卷积、尺度相关、平均尺度与带宽、尺度能量密度、短时尺度变换、瞬时尺度、尺度不确定理论、联合尺度表示等概念。连续信号f(t)的ST与逆ST(inverse ST, IST)定义为

(26)

(27)

式中:Df(c)为信号f(t)的ST;c为尺度;S[·]、S-1[·]分别为ST和IST表示符号。联系式(25)可知

Dh(c)=exp(iclnα)Df(c)

(28)

计算式(28)中IST,得到

(29)

利用ST与IST能够实现TS操作,首先计算信号f(t)的ST得到Df(c),再进行相位修正得到exp (iclnα)Df(c),最后计算exp (iclnα)Df(c)的IST,得到f(t)的TS后信号h(t)。

3.2 尺度互相关函数计算方法

本节利用ST给出SCCF数值计算方法,为方便分析,重写式(17)如下:

(30)

式中:Φuv(α)为连续信号u(t)、v(t)的SCCF。计算SCCF的ST,得到

(31)

容易得到

(32)

图3 SE计算流程

(33)

(34)

ST、IST可分别利用FFT、IFFT快速实现,其中,为得到FST,在计算FFT前需要对f(t)进行指数采样和幅度修正,而为得到IFST,计算IFFT后需要再进行对数采样和幅度修正。为计算SCCF需要进行两次FST、一次复数点乘和一次IFST,总共需要复乘次数为4NlnN+1.5(NlnN)·log2(NlnN),计算复杂度为O[(NlnN)log2(NlnN)]。

4 仿真结果与分析

4.1 基本参数设置

窄带条件下,雷达载频为0.5 GHz,脉冲重复频率10 kHz,相参积累个数为128,雷达发射基准LFM信号时宽20 μs,带宽10 MHz,采样频率40 MHz,尺度因子等间隔取值,取值范围为0.5～2,利用TS产生脉间捷变LFM波形;目标初始距离6 km,径向速度15.3 km/s,模糊数为10,不模糊速度300 m/s。为直观显示,图4给出第1、32、64、96和128个脉冲重复周期雷达发射波形,不同重复周期雷达发射波形时宽、幅度均不相同,其中,第1个脉冲重复周期发射信号时宽最大(40 μs),第128个脉冲重复周期发射信号时宽最小(10 μs),分别对应尺度因子0.5和2的情况。

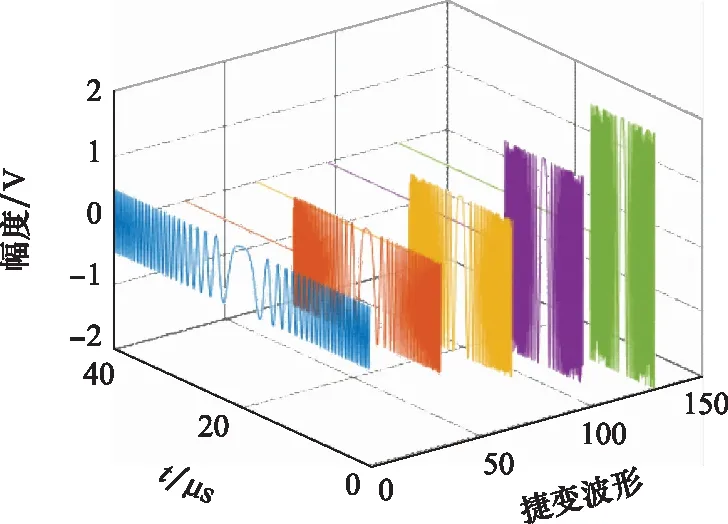
图4 雷达捷变LFM波形

4.2 可行性仿真分析

本节利用3个仿真试验,分别对所设计脉间捷变LFM与相参雷达兼容性问题、所提尺度互相关函数计算方法和波形捷变下的雷达相参积累算法可行性进行验证。为显示细节,仿真回波中均不添加噪声,第4.3节将进行算法抗噪效能验证。

4.2.1 仿真试验1

本文提出一种新颖的脉间捷变波形设计方法,即对基准波形进行不同尺度因子下的TS操作,将TS后信号作为捷变波形。本节重点对该波形与相参雷达兼容性问题以及对目标的影响进行仿真分析。设目标速度模糊数为0,此时目标未出现距离走动,雷达接收基带回波如图5(a)所示,受捷变波形影响,不同重复周期目标回波时宽、幅度均不相同,利用当前重复周期雷达信号对回波进行脉冲压缩,结果如图5(b)所示,不同重复周期目标峰值均解决于1(图中已利用基准波形对目标幅度进行了增益归一化),利用FFT沿慢时间进行相参积累,结果如图5(c)所示,峰值搜索可得目标初始距离为6 km,径向速度为319 m/s,与仿真设置参数基本一致。进一步分析捷变波形对目标主副瓣影响,分别沿距离维、多普勒维对图5(c)中的目标进行切割投影,图6给出了雷达波形捷变与波形不捷变下目标距离维、多普勒维主副瓣对比,当雷达处于波形捷变状态时,所设计波形能够确保目标距离主瓣不展宽前提下,大幅降低距离旁瓣(旁瓣能量泄露至多普勒平面),而目标多普勒维主、副瓣与正常不捷变状态相差不大。

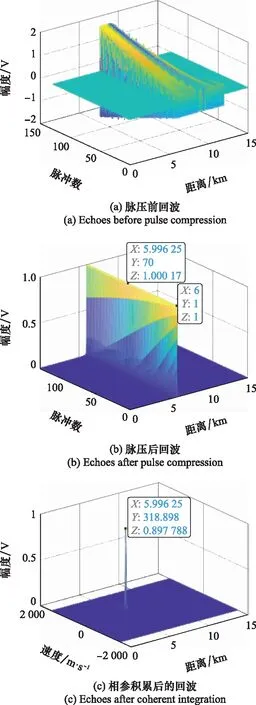
图5 雷达波形捷变下的目标回波

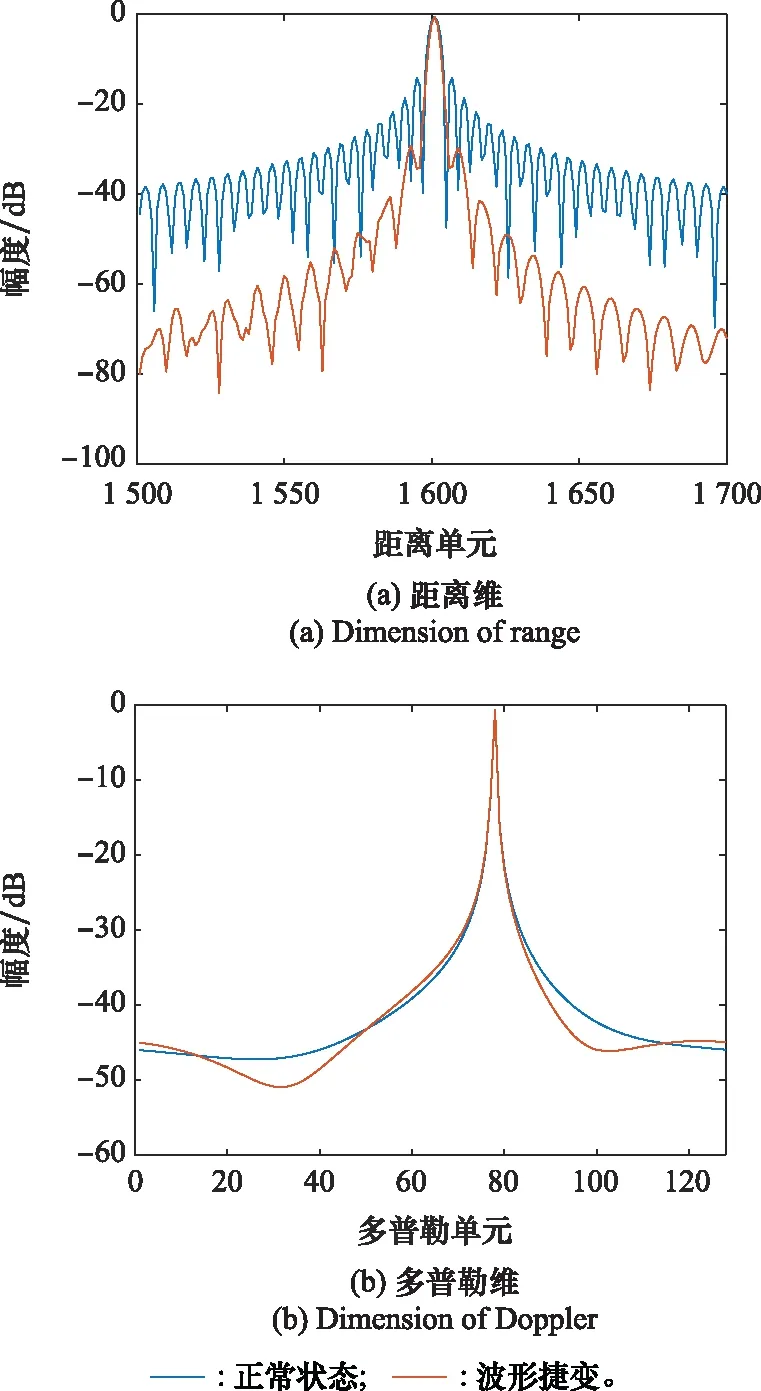
图6 线性尺度因子下的目标主副瓣对比

图6仿真结果是基于线性尺度因子捷变波形,设尺度因子取值范围、间隔同第4.1节,雷达不同重复周期发射波形对应的尺度因子在上述范围中随机选取,在此前提下,雷达波形捷变与波形不捷变下目标距离维、多普勒维主副瓣对比如图7所示。可以看出,波形捷变条件下的目标距离旁瓣同样更低,多普勒维旁瓣与正常不捷变状态相差不大。

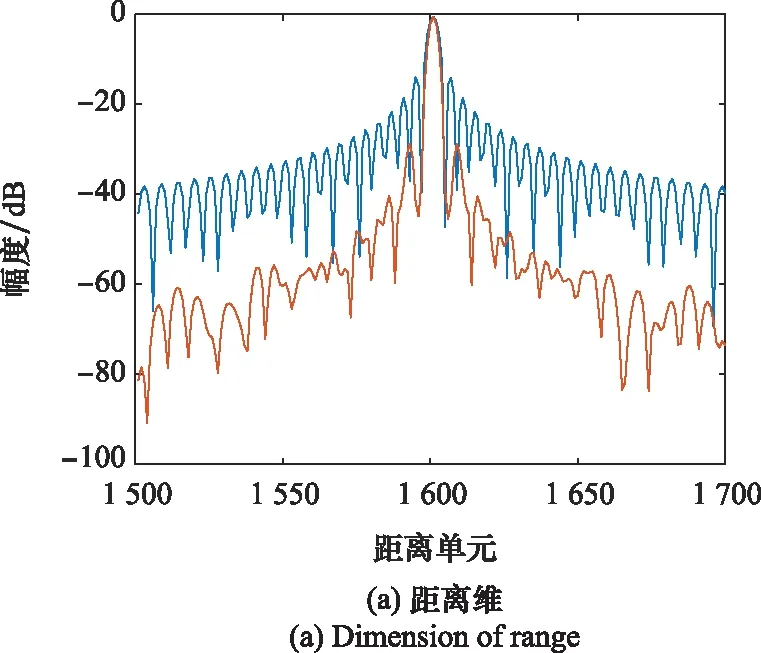
图7 随机尺度因子下目标主副瓣对比

4.2.2 仿真试验2

本节对基于尺度变换的尺度互相关函数计算方法进行验证。取雷达发射第1、128个捷变LFM信号,分别命名为波形1和波形2,如图8所示,计算其尺度变换结果如图9所示,两者包络基本相同。根据尺度互相关函数实现流程,再计算基准波形尺度变换,结果如图10所示,包络与捷变波形尺度变换包络基本相同,反应了尺度变换的尺度不变性。最后,分别计算波形1、波形2的尺度变换(共轭取反)与基准波形尺度变换点积,通过逆尺度变换可得尺度互相关函数,结果如图11所示,峰值搜索可得波形1、波形2与基准波形的尺度因子分别为0.5和2,与仿真设置参数一致。

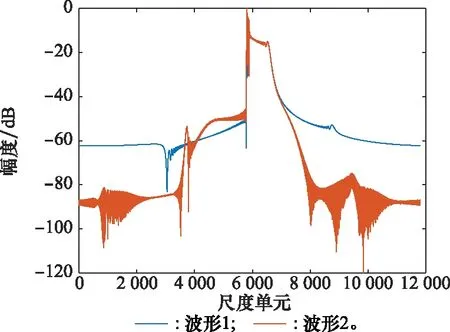
图9 捷变波形快速尺度变换

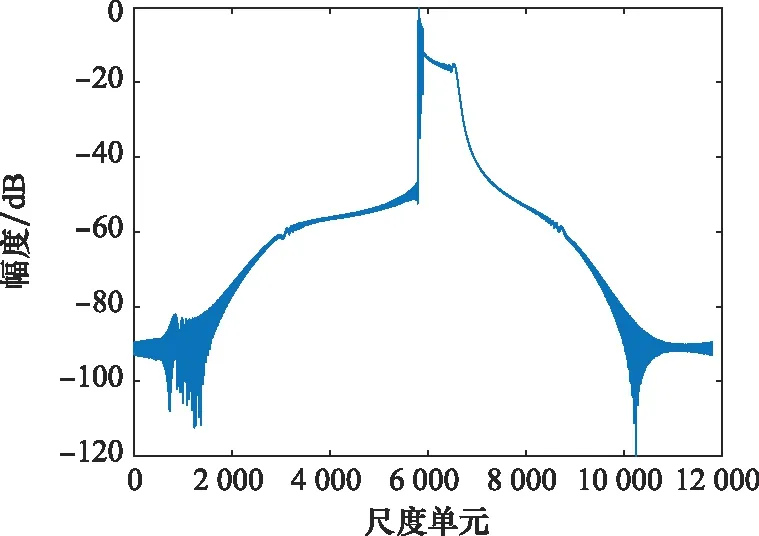
图10 基准波形快速尺度变换

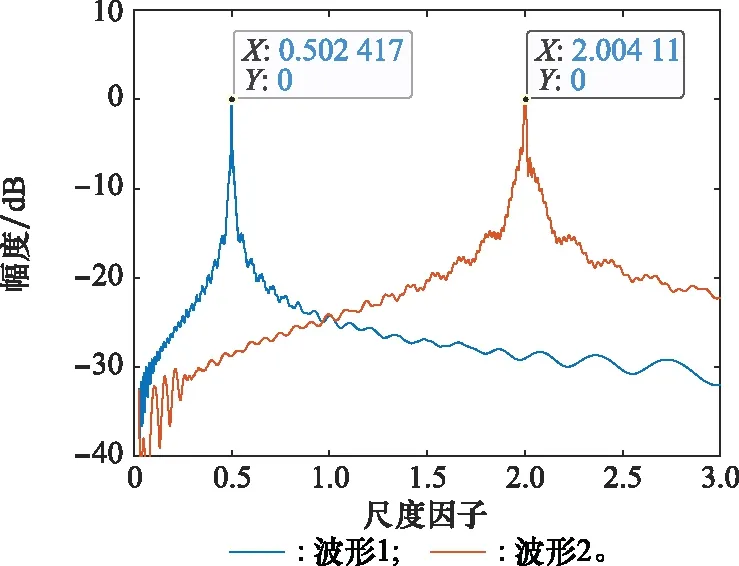
图11 SE结果

4.2.3 仿真试验3

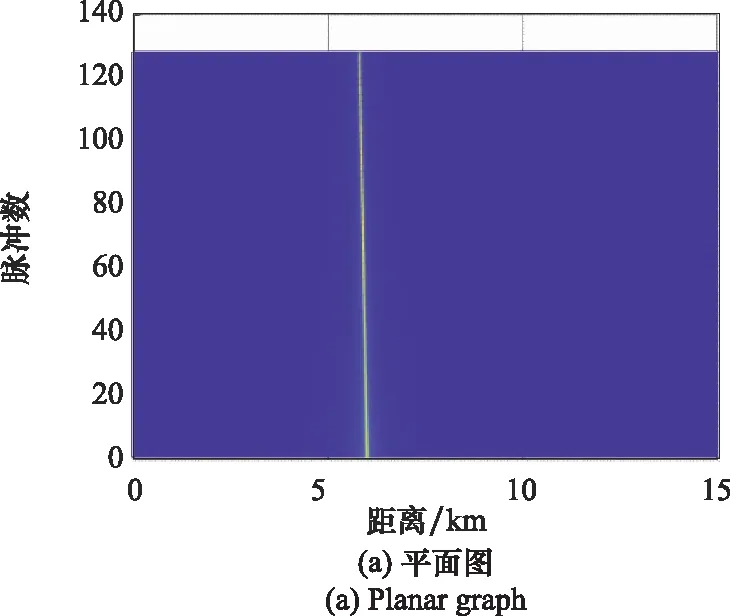
图12 脉冲压缩后回波

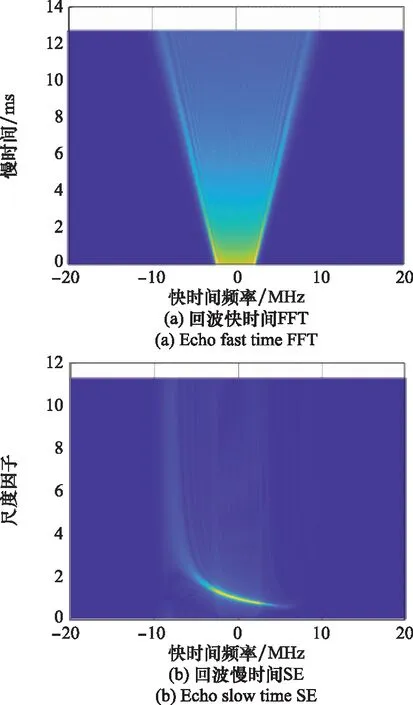
图13 回波快时间FFT及慢时间SE结果

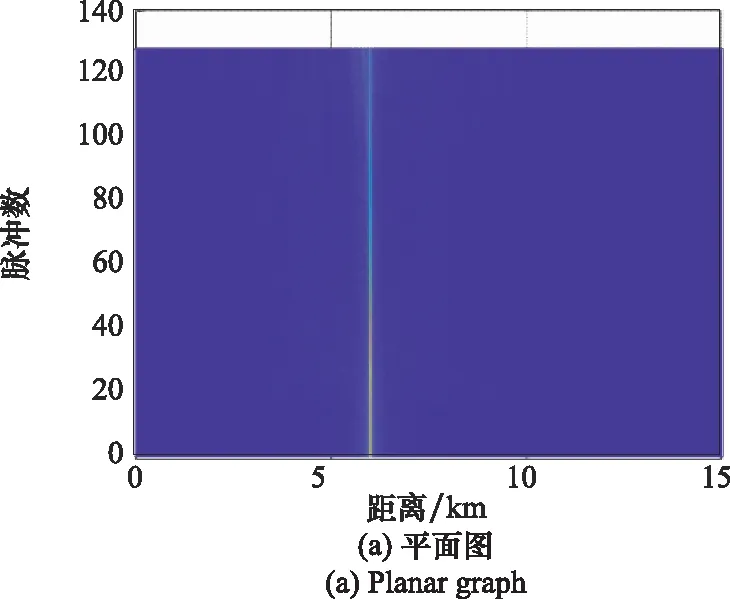
图14 距离走动校正结果

最后,沿慢时间对距离走动校正后的回波进行FFT完成相参积累,结果如图15所示,校正前目标能量较弱,校正后目标能量得到有效积累,峰值搜索可能目标径向距离为6 km,不模糊速度为319 m/s,与仿真参数基本一致,需要注意的是,由于算法缺乏模糊数补偿环节,无法得到目标真实径向速度。

图15 回波相参积累结果

4.3 抗噪效能仿真分析

本节对比现有几种KT实现方法,即辛格插值法[21]、Chirp滤波法[22]、线性调频Z变换(chirp-z trarsform,CZT)+IFFT方法[23-24]、FFT插值法[25-26]以及基于MT的KT实现方法[17],对所提基于SE的非标准KT实现方法抗噪效能进行验证。设信噪比(signal to noise ratio, SNR)取值-20～5 dB,间隔2 dB,其他参数同第4.1节,运行蒙特卡罗仿真500次,目标检测率(target detected ratio, TDR)随SNR变化曲线如图16(a)所示,将雷达载频提升至1 GHz,其他参数不变,同样运行蒙特卡罗仿真500次,TDR随SNR变化曲线如图16(b)所示。

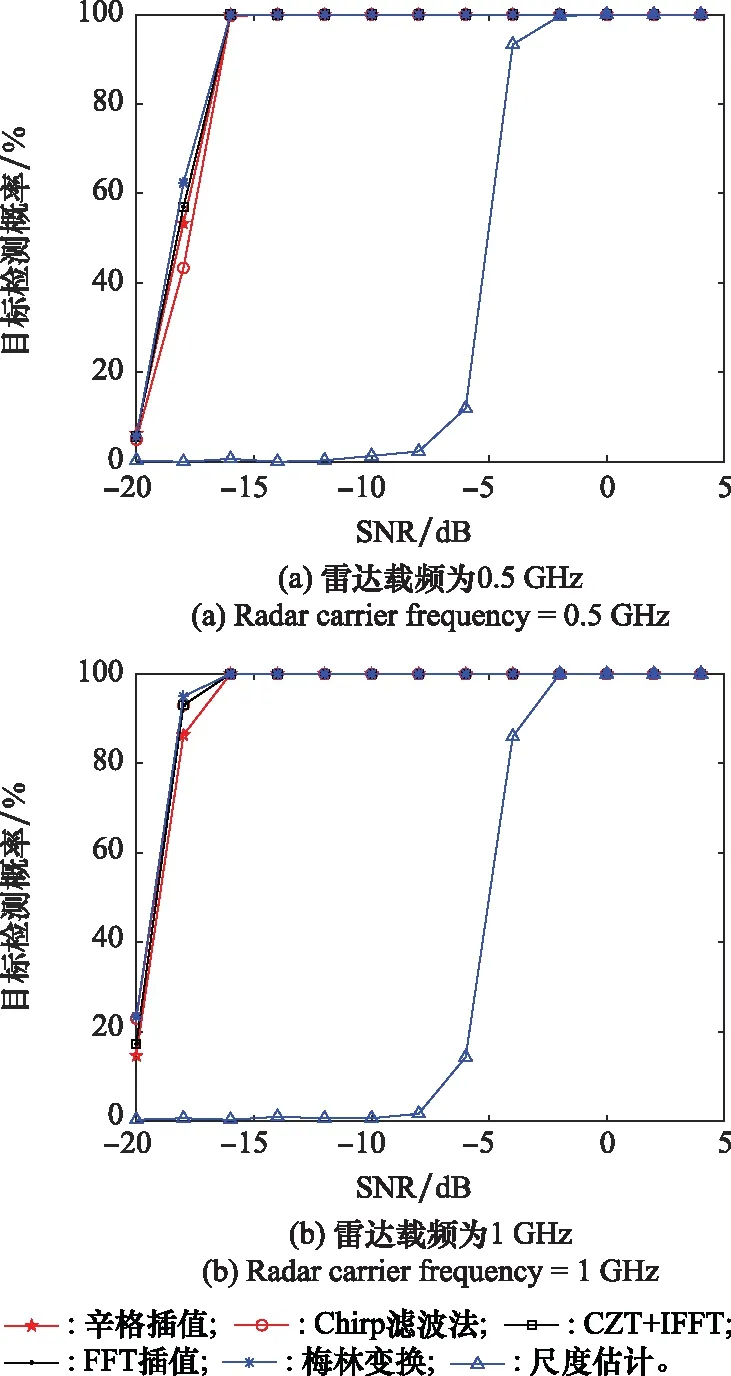
图16 TDR随SNR变化曲线

所提非标准KT抗噪性能明显低于其他5种方法,分析原因是因为该方法要求对非零频慢时间信号进行SE,然后再进行时间尺度,由于缺乏峰值对比环节,算法受噪声影响更大。另外,5种标准KT实现方法需要对不同模糊数补偿下的目标峰值进行比对,实际上已利用了回波脉压、相参积累增益[27-30]。考虑到,所提方法无需搜索模糊数,当SNR较高时同样具有一定的应用价值。

5 结 论

针对波形捷变雷达相参积累问题,提出非标准KT的波形捷变雷达相参积累算法。文中基于时间尺度操作,设计了一种新颖的脉间捷变LFM波形,不仅解决了与雷达体制兼容性问题,还可在目标主瓣不展宽的前提下有效抑制目标距离旁瓣。另外,针对目标高速运动容易出现的跨距离门问题,提出非标准KT,与标准KT相比,非标准KT无需模糊数补偿,可解决波形捷变雷达目标距离走动校正难题,缺点是对信噪比要求较高,无法得到目标真实模糊数。