三线摆法与扭摆法测量物体转动惯量之比较

王兴福,葛智勇

(南京邮电大学 理学院,江苏 南京 210023)

随着国家中长期教育改革和发展规划纲要的推出,高校如何进一步优化实验教学体系,提高教育教学质量,提升学生创新能力,是高等教育内涵式发展必须解决的问题[1]。实验教学比较研究有利于帮助教师有效深度备课,充分吃透教材,准确把握目标,提升教学层次,有利于帮助学生加深实验理解,培养思维训练,激发创新能力,以适应越来越快的知识更迭和应对愈来愈烈的竞争压力。实验教学比较研究的内容包括实验教学理念、实验教学体系、教学内容、教学方法、评价考核方式以及设备和环境条件等[2,3]。本文选取大学物理实验中一个重要的物理量——转动惯量,对两种测量方法的实验进行详细的教学内容比较研究。

转动惯量是表征刚体转动惯性大小的量度,其量值取决于物体的形状、质量分布及转轴的位置,而与绕轴转动状态(如角速度的大小)无关。与平动中用质量表征物体惯性大小一样,刚体的转动惯量有着重要的物理意义,也是科学实验、工程技术、航空航天、仪器仪表等工业领域一个重要参量。对于几何形状规则、质量分布均匀的物体,其转动惯量可根据公式I=∭Vr2dm计算得出,式中dm表示刚体的某个质元的质量,r表示该质元到转轴的垂直距离。对于几何形状不规则或质量分布不均匀的物体,用数学方法计算是非常困难的,其转动惯量通常采用实验的方法进行测定。实验上,测定刚体转动惯量的方法很多,常用的有三线摆法[4-8]、扭摆法[9-12]、复摆法和落体法等。在物理专业实验教学中,常常要求学生比较三线摆和扭摆法之异同,本文将从以下几个方面作出详细比较。

1 实验原理之比较

三线摆实验装置包括水平固定的上圆盘和由悬线与之相连的下圆盘,一起悬挂在转轴上。三根悬线对称分布,且长度可调节,从而使下圆盘处于水平状态,下圆盘可绕中心轴作扭转运动。当下圆盘摆动角度很小且忽略空气阻力时,其运动可近似看作简谐运动。将待测物体放置于下圆盘,并使其质心通过中心轴,则物体和下圆盘绕中心轴的转动惯量为

(1)

式中,m为下圆盘和待测物体的总质量;r、R分别为上下悬点离各自圆盘中心的距离;H为平衡时上下盘间的垂直距离;T为下圆盘作简谐运动的周期,g为重力加速度。

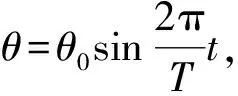
扭摆的垂直轴上装有一根薄片状的螺旋弹簧,用以产生恢复力矩。在轴上方有螺旋接口,可以安装各种待测物体。垂直轴与支座之间装有轴承,使摩擦力矩尽可能小。可通过调节底脚螺丝钉使垂直轴与水平面垂直,一般仪器上装有水准仪,用来检测系统是否达到水平状态。将物体在水平面内转过一定角度后,在弹簧的恢复力矩作用下,物体就开始绕垂直轴作往返扭转运动。则物体绕垂直轴的转动惯量为

(2)

式中:K为弹簧的扭转常数;T为简谐运动的周期。

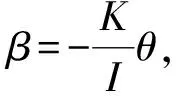
从公式推导过程可知,在两种测量方法中,待测物体均作摆动而非转动,都使用了刚体转动定律。在忽略摩擦力矩前提下,都是看成简谐振动,故均需使用运动方程。不同点在于三线摆的摆角较小,一般不超过5°,这样才能在推导过程中采用近似和忽略的方法。

2 实验内容之比较

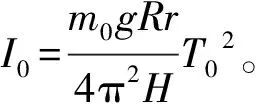
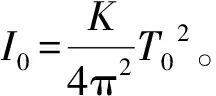
三线摆中的下圆盘与扭摆中的载物盘有着相同的作用,可用来承载待测物体。相对于待测物体,他们的质量不可忽略,且尺寸较大,故其转动惯量是不能忽略的,在计算时要将其减去。三线摆的下圆盘上不能固定待测物体,仅靠其自重产生的摩擦力保证摆动过程中的稳定,故能测量的物体种类较少,扩展性较差。扭摆的转轴上方有螺旋接口,可以安装多种几何形状的待测物体,如实验中常常还会测量金属细杆和木球的转动惯量,因其自带螺旋接口,就不再需要金属载物盘来承载。实际上,相对于待测物体而言,螺旋接口的质量和几何尺寸均较小,其转动惯量是可以忽略的。所以,对于这两种形状的待测物体,仅需测量摆动周期,应用公式(2)即可得出其转动惯量实验值,测量过程更加快捷。从这里也可看出,扭摆弹簧的扭转常数也可通过测量金属细杆得到,该方法更为简便,只需测量细杆的摆动周期,连同其转动惯量理论值一起带入公式(2)即可。不过,在测量细杆质量时,一定要将接口支架取下,否则视为其质量均匀分布到细杆上,造成测量结果严重偏大。在扭摆实验的待测物体中,设置了质量相同的一个塑料圆柱和一个金属圆筒,圆柱的直径与圆筒外径相等,高度也相等。这样可以很清楚地说明,刚体的转动惯量与质量分布的关系。显然,在质量相同的情况下,质量分布更远离转轴的圆筒的转动惯量要比圆柱的大。

3 验证平行轴定理之比较

若质量为m的物体绕质心轴的转动惯量为IC,当转轴平行移动距离x时,则物体对新轴的转动惯量为I=IC+mx2,这就是转动惯量的平行轴定理。

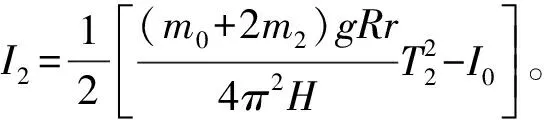
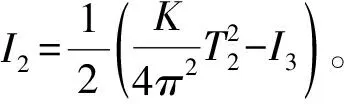
两种测量方法均采用对称放置两个小圆柱,因为两力矩大小相等,方向相反,相互抵消,减小测量误差,保证仪器摆动的稳定性,减少磨损,延长使用寿命。实际上,两种测量方法放置小圆柱的方向是不同的,三线摆中小圆柱是竖向放置,而扭摆中是横向放置的,这也可以从转动惯量理论值公式中可以看出区别,但对验证平行轴定理而言,放置方式并无本质区别。

4 实验操作之比较

两种测量方法在实验操作上有很多相同或相似点。(1)在仪器调节方面,首先要做到使转轴位于竖直状态。三线摆通过调节悬线摆长,一般另配有水准仪,可放置于下圆盘中心。而扭摆自带水准仪,通过调节底脚螺钉,来检测是否达到水平状态。(2)在周期测量方面,扭摆装置配备了转动惯量测试仪,包括光电探头和主机,光电探头采用红外发射管和红外线接收管,用光电探头来检测挡光杆是否挡光,根据挡光次数自动判断是否已达到所设定的周期数。传统的三线摆计时方法也同单摆类似,采用秒表由人工数数计时。随着设备的升级,一般也另配备了光电计时器,通过记录某一根悬线的挡光情况,即可测出摆动周期,实现了和扭摆相同的自动计时。(3)质量称量方面,都采用了数字式电子台秤,将待测物体放在秤盘上即可从显示窗直接读出该物体的质量。(4)在尺寸测量方面,都使用了游标卡尺测量圆环、圆柱体的直径、高度等数据,对于较长的金属细杆选用卷尺进行测量。

两种测量方法在实验操作上存在一些不同。为保证三线摆做简谐振动,其扭转角度必须小于5°,操作时为减小下圆盘的晃动,一般轻轻小角度转动上圆盘,从而带动下圆盘转动。而扭摆的金属载物盘与转轴是连在一起的,不存在稳定性的问题。但由于弹簧的扭转常数K值不是固定常数,它与摆动角度略有关系,摆角在40°～90°间基本相同,实验时为了降低摆角变化过大带来的系统误差,在测定各种物体的摆动周期时,摆角不宜过小、变化过大,且整个实验中摆角基本保持在这一范围内。在摆放待测物体时,三线摆的下圆盘上有同心圆线和交叉线,使得待测物体与下圆盘中心重合;而在验证平行轴定理时,对称放置的两个小圆柱也是以此线为参照。而扭摆的金属载物盘内径和待测的圆柱、圆筒外径一致,并可用挡光杆固定。换测细杆和验证平行轴定理时,可根据细杆上的凹槽确定支架和小圆柱的位置。

5 数据处理之比较

由于待测物体一般都选用几何形状规则的物体,故两种测量方法都可将质量和尺寸等数据代入计算公式,求出这些物体的转动惯量理论值,从而将实验值与之进行比较,进行百分差(即相对误差)的计算,以此对测量作出评价,一般都不要求计算不确定度。以下选取同一个塑料圆柱,分别在两种仪器上进行测量。扭摆法测量数据见表1。

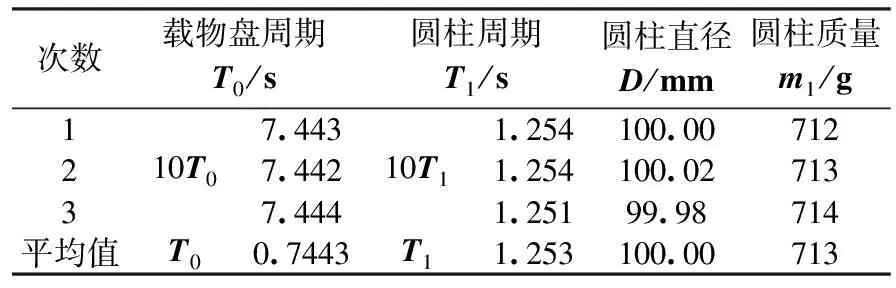
表1 扭摆法测量数据表

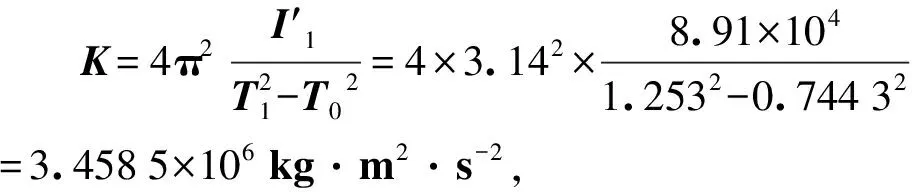
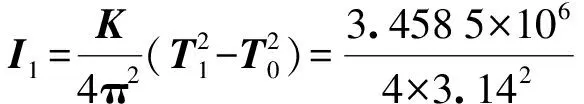
(1.2532-0.744 32)=8.91×10-4kg·m2。

三线摆法测量数据见表2。

表2 三线摆法测量数据表

根据测量结果,计算圆柱转动惯量的过程如下:

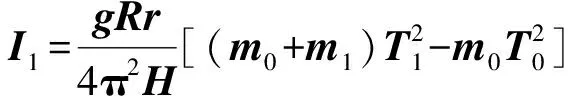
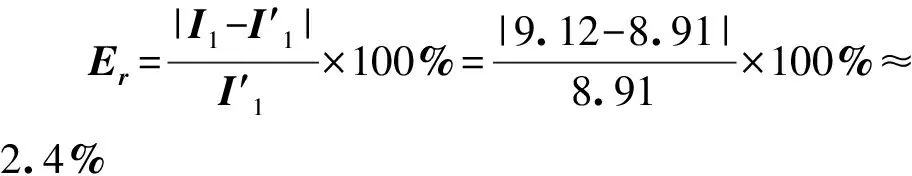
由于求解扭转常数K的过程使用了圆柱转动惯量理论值,这是传统扭摆法通常采用的倒推法求扭转常数K的方法,所以实验值必然与理论值相等。不过,也可以理解为圆柱是用来求K值的标准件,而其他物体为实验待测物体。实际上,实验过程中的扭转常数K并不是恒定值,在此不再赘述。针对倒推法的弊端,王维光[10]提出了改用“定义法”直接测量K值,从而将“几何法”与“扭摆法”隔离,并重新设计了实验内容,使实验条理更加清晰。以上通过这两种方法的测量数据比较,并不能得出哪种方法更准确的判断,仅仅想由此展示求解过程的不同。

6 结 论

刚体是大学物理课程中的重要模型,转动惯量是反映其运动的重要物理量。本文通过从实验原理、实验内容、实验操作和数据处理等多个方面,全面比较了三线摆和扭摆两种测量物体转动惯量的方法。这样的教学比较有利于帮助学生在实验中找出差异、总结共性,加深对转动惯量测量的理解,同时也对授课教师深度备课,开展教学研究,起到积极的借鉴作用。这样的教学比较研究也可以推广到其他实验中,如静态法、动态法测量物体的杨氏模量,惠斯通电桥测中值电阻和双臂电桥测低电阻等。教学比较研究也可推广到其他课程的教研实践中,尤其是理工科院校,可根据实际情况,多开展此类教学研究活动。