群论思想在代数组合中的渗透与应用

闫 焱 邓明立

(1.河北师范大学 数学科学学院,石家庄 050024;2.华北理工大学 理学院,唐山 063210)

代数组合(Algebraic Combinatorics) 是组合数学与抽象代数的交叉学科,其研究对象涉及可以被组合学和代数学解释的对象。以美国数学会所编列的数学科学分类系统(2010) 为例,在05Exx代数组合项下包括各研究子类如下：对称函数及推广;表示论的组合方面;代数几何的组合方面;群与代数的组合方面;组合结构上的群作用;结合方案、强正则图;交换代数的组合方面;单纯复形的组合方面。尽管目前代数组合仍然是一个发展中的领域,但是其源头可以追溯到18世纪欧拉(L.Euler,1707—1783) 关于划分的思想、结果和方法,它们在近几十年被广泛应用于代数组合与群表示理论中。代数组合开始被尝试系统地进行研究应该归功于20世纪60年代罗塔(1)罗塔(G.C.Rota,1932—1999) 是意大利裔美国数学家和哲学家,他的数学研究始于泛函分析、微分方程、概率论和遍历理论等相关领域,在概率和遍历理论问题的激励下,他在20世纪60年代早期转向组合数学。当很多人认为组合数学充其量只是一堆聪明孤立的技巧时,罗塔观察到了组合数学与众多抽象数学分支的相互作用和相关性。罗塔在组合数学基础方面的工作集中于揭示隐藏在不同组合领域背后的代数结构,他因在组合数学上的重大贡献而成为名闻数学界的杰出数学家,组合数学的复兴很大程度上要归功于罗塔对这一学科的独特见解,他被公认为促成这一转变的主要人物之一。(G.C.Rota,1932—1999) 的影响,在他的推动下组合数学逐渐被纳入了现代数学的主流,代数组合也得以逐渐发展成为一门日趋完善的学科。

20世纪以来,代数学的研究对象及研究方法不断更新开拓,特别是1930—1931年数学大师范德瓦尔登(B.L.van der Waerden,1903—1996) 出版的《近世代数学》确定了代数结构化的思想形成,成为了数学代数化趋势的思想源泉,这部以“结构”为指向的“近代代数学”从根本上改变了代数学的整个面貌[1-2]。代数以其结构的一般性,不仅是集合、符号和思维的语言,而且实现了将许多种类各异的、高度数学化的学科进行代数化处理。代数学的思想和方法推动了代数数论、代数拓扑、代数几何、代数组合等交叉学科的发展。因此,从结构数学的视角分析“组合问题中的代数思想与方法”具有十分重要的研究意义,这不仅可以透视出如何利用代数方法或者结论研究组合问题,同时亦可以从组合学的视角为一些抽象的代数结果给出具体的解释。

在国际数学界,代数组合被视为“组合对象的表示理论”或者“没有群的群论”,尽管罗塔、斯坦利(R.P.Stanley,1944— )、坂内英一(E.Bannai,1946— ) 等众多数学家撰写了一系列关于代数组合的论著,但是这些论著多以代数组合的学术成果与学术进展综述为主,还没有基于群论思想研究代数组合学科历史的论著。鉴于此,笔者在掌握原始文献和研究文献的基础上,选取了代数组合中具有基础性、核心性及统一性的概念——“结合方案”作为研究切入点,针对结合方案及其相关问题(代数理论、特征理论及结构理论) 进行展开,探究了结合方案历经了哪些发展才形成了今天的概念表述?哪些关键的历史人物起到了重要的引领作用?通过分析代数组合和群论的共同逻辑基础、共同概念基础和共同方法基础,揭示在代数组合的创立与发展过程中,群论的思想和方法是如何被继承、发展或突破的,进而展示出群论思想和方法在代数组合领域中呈现出的交叉与融合、渗透与应用。这些问题无论在数学史上还是在数学研究方面,甚至在学科间交叉应用的历史研究上都值得我们寻本溯源。

1 代数组合作为一门学科的诞生

代数组合这门学科的研究历史可以与群的特征理论媲美,包括弗罗贝尼乌斯(F.G.Frobenius,1849—1917)、舒尔(I.Schur,1875—1941) 和伯恩赛德(W.Burnside,1852—1927) 的研究理论。特别是20世纪30到60年代群论专家维兰德(H.Wielandt,1910—2001) 和希格曼(2)唐纳德·戈登·希格曼(D.G.Higman,1928—2006) 是美国数学家,被认为是在有限群、表示理论、代数组合以及几何学方面重要理论的缔造者。他在群论研究中引入了组合的方法,从而产生了新的理论和方法,开辟了一条新道路,促进了现在被称为“代数组合”领域的发展。希格曼被视为该领域的创始人之一。(D.G.Higman,1928—2006)等人关于有限置换群的工作(置换群的中心化子环)[3-5],由此开辟了一条新的道路,促进了代数组合领域的发展。

“代数组合”一词首先是坂内英一于1979年在日本著名刊物《数学》(Sugaku)(3)日本著名数学年刊《数学》是1947年4月创刊的日文杂志,现在每年发行4次,主要刊登日本数学会会员的有关数学的论述、书评、学界新闻等。论述是以让专业以外的人亦能欣赏和理解为目的的综述文章,其中大部分被翻译成英文,由美国数学会以Sugaku Expositions的杂志名发行。上发表的《代数组合论》(代数的組合せ論)[6]这篇评论性文章中提出的,由此宣告了这门学科的诞生。尽管“代数组合”一词首次出现在他1979年的文章中,但事实上这个词此前已经萦绕在他脑海中很多年了,虽然当时已经有了代数图论,代数编码等词,但是坂内英一希望创立一个术语,该术语不但能涵盖这些领域,也能够表达这一数学思想体系。

1984年坂内英一与伊藤达郎(T.Ito,1948—)(4)日本数学家伊藤达郎(T.Ito,1948— ) 是目前国际上代数组合研究领域的知名学者之一,他与坂内英一的工作情谊起于伊藤达郎的本科阶段。伊藤达郎曾应坂内英一之邀,两次在俄亥俄州立大学进行为期一年的访问。在第一次访问(1980—1981,任访问助理教授) 期间,促成了1984年系统论述代数组合的第一部专著《代数组合I：结合方案》的出版。出版了系统论述代数组合的第一部专著《代数组合I.结合方案》(AlgebraicCombinatoricsI.AssociationSchemes)[7],旨在介绍代数组合这门学科,但是当时对于代数组合尚没有明确的定义,书中首次正式使用“代数组合”一词,术语“代数组合”开始被广泛使用,该书亦成为了代数组合发展过程中的一个里程碑。1992年为适应代数组合研究蓬勃发展的需要,《代数组合学》(JournalofAlgebraicCombinatorics)杂志创刊。

图1 1979年坂内英一在日本著名刊物《数学》上发表了题为《代数组合论》的评论性文章

图2 1984年坂内英一与伊藤达郎出版了系统论述代数组合的第一部专著

尽管“代数组合”这一名词出现在20世纪70年代,但是它所涉及的某些经典核心问题却历史悠久,比如结合方案的相关问题。坂内英一曾这样写道：“在代数组合中,结合方案是非常基本的概念,也许是最重要的。”([7],7页) 事实上,结合方案与距离正则图、码、设计等诸多代数组合研究领域都存在着千丝万缕的联系[8-12],且在代数组合发展过程中极具代表性。结合方案的数学思想可以追溯到18世纪欧拉对分拆的研究。

在组合学史上,欧拉曾巧妙地解决了一些经典组合学问题并引入了重要的方法[13]。他对于组合学发展所做的主要工作有四个方面：整数分拆、错位排列、欧拉方阵猜想和计数函数。整数分拆问题最早是莱布尼兹(G.W.Leibniz,l646—1716) 在1699年给伯努利(J.Bernoulli,1667—1748) 的信中提到的。欧拉对整数分拆问题的研究源于1740年诺地(P.Naud,1684—1747) 给他的一封信。信中诺地指出了一个有趣的问题：一个正整数可以用若干个不同或者相同的正整数的和来表达的方法有多少种?针对这个问题,欧拉凭借敏锐的洞察力发现了许多数字分拆的新思想、新结果和新方法。比如他发现：分拆数的计算与二项式的乘积有着特定的联系,并最终把这个组合问题与幂级数联系起来,从而使得分拆问题转化为幂级数中x非零次幂的系数与指数的关系。在此基础上,欧拉又考虑了二项式无穷乘积的倒数与分拆数的关系。欧拉指出：“把一个正整数分拆为不同正整数与分拆为可重复的奇数的分拆数相等”,并在其《无穷分析引论》(IntroductiontoAnalysisoftheInfinite) (1748) 的第16章中发展了这种思想[14],整数分拆问题为以后类似的分拆问题研究开辟了新的思路。在近现代数学中,特别是在数学和统计问题中,当对离散对象进行计数、分类等研究时,可以有效地应用数的分拆理论来研究这些问题。最近几十年,它在代数组合与群表示理论中被广泛地应用。那么分拆理论是如何渗透到结合方案这一概念中的?这就要提到C-代数(特征代数) 的划分、统计试验中的单元划分以及结合方案中的结合关系。

在组合学发展的黄金时期,数学家们已经为代数组合领域做出了许多重要的奠基性工作,但是没有给出结合方案的确切定义,更没有将结合方案理论系统化。数学家们虽然在工作中大量使用了结合方案的概念,并给出了许多结合方案的重要结果,但是都没有明确提出结合方案这一术语。比如,结合方案的概念曾以C-代数的形式被研究。C-代数能够引起关注是源于1942年川田(Y.Kawada) 的一篇论文《关于非交换群特征的对偶定理》(über den Dualitätssatz der Charaktere nichtcommutative Gruppen)[15],但是这篇论文从发表到引起关注经过了很长一段时间。不过幸运的是最终还是被致力于结合方案和置换群的学者们注意到了。这篇论文的撰写动机起源于霍海塞尔(G.Hoheisel,1894—1968) 在1939的研究工作[16],当时霍海塞尔在论文《关于特征》(über Charaktere) 中为有限群G建立了一种代数结构(现在被称为“交换结合方案”),他计算了所有参数之间的关系,特别是G的特征标表的正交关系。川田从霍海塞尔的工作中提炼出了形如“交换结合方案”的抽象概念,并称之为C-代数,即：

假设A是一个在线性空间意义上以x0,x1,…,xd为基的C上的代数,如果满足以下(i)-(vi)条,则A和x0,x1,…,xd称为C-代数(特征代数)：

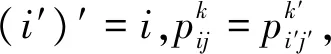
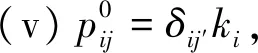
(vi)映射xi→ki(i=0,1,…,d)是A的一个线性表示。

川田在上述定义的基础上对C-代数的参数关系进行了计算,进而又对C-子代数和商C-代数进行了研究。值得注意的是,当霍海塞尔和川田进行他们的研究时,结合方案的概念在组合学的语境中并不存在。川田提出的C-代数的概念,在代数上和现在所说的交换结合方案的概念是一样的。川田建立了C-代数公理,并发展了结合方案的所有代数性质。

在统计学试验中,当费希尔(R.A.Fisher,1890—1962)最初主张将统计试验中的单元划分为相似单元的区组时,他提出了每个处理应该在每个区组中的一个单元上进行,这种设计后来被称为随机区组设计或者完全区组设计。然而这种设计有其一定的局限性,使得自然区组可能不够大,以致于不能容纳所有处理。比如在农业田间试验中,当每块或每行或每列的地块数量超过10或12块时,费希尔著名的随机区组和拉丁方设计的效率就会下降。因此,叶特斯(F.Yates,1902—1994) 引入了不完全区组设计,他凭直觉提出了这样一种设计：每对处理在相同数量的区组中同时进行。叶特斯称这种设计为对称的不完全随机区组排列,现今统计学家称之为平衡不完全区组设计,而数学家称之为2-设计。

随后,1939年统计学家玻色(R.C.Bose,1901—1987) 和内尔(K.R.Nair) 在论文《部分平衡不完全区组设计》(PartiallyBalancedIncompleteBlockDesigns) 中基于试验设计背景提出了部分平衡不完全区组设计这一概念[17],这项工作的意义是在叶特斯工作的基础上提出了更广泛的一类设计(即为平衡不完全区组设计的一种推广,简记为PBIBD),由此部分平衡设计的其他特例也开始被广泛研究并应用。

为了研究部分平衡不完全区组设计的构造问题,玻色和岛本(T.Shimamoto) 发现两个结合类的部分平衡设计具有重要的性质。1952年玻色和岛本在一篇关于统计(组合) 设计理论的论文《具有两个结合类的部分平衡不完全区组设计的分类与分析》(ClassificationandAnalysisofPartiallyBalancedIncompleteBlockDesignsWithTwoAssociateClasses) 中引入了结合方案的思想,此处的结合方案是一个纯粹的组合结构[18],用它描述具有多个结合关系的处理之间的某种平衡性。玻色和岛本以简化和紧凑的形式给出了区组内分析、组合区组内分析和区组间分析,这样做可以将某些试验设计划分为少数几个不同的类型,对于每一个类型结合方案都可以明确地展示出来,并简化了数值计算以及对结果的解释。该论文的贡献不仅催生了现今结合方案定义的雏形,还用此概念利用矩阵代数方法对部分平衡设计的分类进行了研究。文章中是这样表达的：一个不完全区组设计称为是部分平衡的,如果它满足如下条件：

(i)试验素材被分为b个区组,每个区组有k个单元,对同一区组的单元进行不同的处理。

(ii)能将v个处理安置在r个区组里。

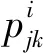
(iv)如果两个处理有第i种关系,则两个处理同时在λi个区组中。

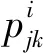
1959年在对结合方案的研究过程中,玻色和梅斯纳(D.M .Mesner)在论文《与部分平衡设计的结合方案对应的线性结合代数》(OnLinearAssociativeAlgebrasCorrespondingtoAssociationSchemesofPartiallyBalancedDesigns)中提出了对于给定一个m类和给定参数的结合方案[19],如果可以将v个对象排列成b个集合(每个集合对应一个区组),那么就得到了一个部分平衡设计,并且给出了一种验证给定结合关系是否满足部分平衡条件的有效代数方法——现在被称为Bose-Menser代数的著名理论,此时论文中的结合方案的定义更加趋向了代数组合化的表述方式：

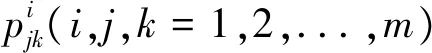
(a)任意两个对象满足唯一的第i种关系(i=1,2,……,m),如果对象α与对象β满足第i种关系,那么对象β与对象α满足第i种关系。

(b)任意一个对象α,则对每一个i,与α满足第i种关系的处理共有ni个,ni与α无关。

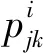
自此“结合方案”随即成为了代数组合领域的研究热点之一。现在普遍使用的结合方案的定义是1973年德尔萨特(P.Delsarte)在他的博士论文[20]《编码理论中结合方案的代数方法》(AnAlgebraicApproachtotheAssociationSchemesofCodingTheory)中给出的,从结构数学的视角来看,该定义比之前玻色和岛本给出的定义更具一般性,因为定义中既包含了由玻色和梅斯纳定义的结合方案中代数理论的元素,又融合了希格曼引入的协调构形的概念,可以说既简洁又不失一般性,具体表述如下：

若一个非空有限集合X满足|X|≥2,R0,R1,…,Rn是X×X的非空子集且满足下列条件：

(i)R0={(x,x)|x∈X}。

(ii)X×X=R0∪R1∪…∪Rn,∀i≠j,Ri∩Rj=∅。

(iii)令tRi={(x,y)|(y,x)∈Ri},对于每个i∈{0,1,…,n},存在i′∈{0,1,…,n}使得tRi=Ri′。

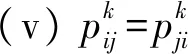
事实上,在上述定义中,R就是X×X=R0∪R1∪…∪Rn的分拆,其中∀i≠j,Ri∩Rj=∅。

将川田在1942年提出的C-代数定义与德尔萨特在1973年提出的结合方案定义进行对比分析(如表1所示),可以看出二者在结构上本质是一样的。

表1 川田的C-代数定义和德尔萨特的结合方案定义对照分析

结合方案作为代数组合中的一个重要研究对象,其研究内容涉及构造、参数计算、结构(子结构,商结构,对偶性、本原性以及自同构等)和分类等问题,这在本质上遵从了群论的研究路线以及结构数学的研究思想。坂内英一曾在论文《作为纯粹数学的组合理论：代数组合的目标》(CombinatoricsRegardedasPureMathematics：theAimsofAlgebraicCombinatorics)[9]中明确表达了他个人对于代数组合研究的主张和信仰,他认为从长远发展考虑应该以纯粹数学的观点为其他领域提供数学支撑。([9],2页)坂内英一对代数组合学科最大的祈愿是从代数组合的角度重塑对有限单群的分类解释和拓展。当然这不是一件简单的事情,需要建立“代数思维”与“代数组合中思维实践”之间的关系,也许这正是20世纪所彰显出来的一种特色趋势——“代数无处不在”。

2 代数组合中的群论思想与方法

自代数组合开始被系统研究以来,许多群论的概念和性质被发现可以推广到结合方案上来,例如：子群、正规化子、有限群的幂零性、西罗定理等。不仅是群中的概念和性质,类似有限群的表示理论,结合方案的表示理论也是研究其数学结构的有力工具之一。这些信息都揭示出一个强烈的信号,一个看似没有群结构的学科(代数组合) 内蕴着强大的群论思想和“没有群的群论结构”。下面将从代数组合的刻画问题、分类问题、结构问题、实现问题这四个方面入手,从中选取代表性问题进行剖析。

2.1 群论视角下对结合方案的刻画

对于统计学家而言,设计只是一个试验方案,而对于组合学家或者代数学家来说,设计就是一种关联结构——结合方案(群的一种自然推广)。数学家更倾向将结合方案理解为纯粹的数学对象。从群论的角度来说,结合方案虽源于纯组合对象,却与群有某种天然的联系,以群论的观点可以视为对可迁置换群性质的公理化结果。

基于群论,结合方案的构造可以从一个群作用一个集合入手。[21]将一个有限群G可迁地作用在有限集合X上且|X|=n>1,即要求对于(x,y)∈X×X,σ∈G,满足(x,y)σ=(xσ,yσ)。G作用在X×X上不再是可迁的,那么由X和R0,R1,…,Rd构成了一个结合方案(不一定满足交换),其中R0={(x,x)|x∈X},R1,…,Rd是X×X上G的d+1个轨道(这里d+1等于任一元素x∈X的稳定子Gx作用在X上的轨道数,价为|Ri(x)|)。从上述结合方案的构造过程可以看出G作用在X×X上产生的轨道构成了结合方案,每个轨道即为结合类或结合关系,研究这些关系以及这些关系之间所具有的性质,并把这些性质一般化,进而推广到一般的组合结构中,这就是结合方案的概念公理化。

事实上,利用有限群构造结合方案的方式是不唯一的,即结合类(结合关系) 的构造方式很多。比如同样是有限群X,可以利用它的右平移群T(X)和内自同构群G0来生成一个新的群G=,而这样的群G可以可迁地作用在X上,从而可以构成一个交换的结合方案(X,{Ri}0≤i≤d),其中d+1为X的G0轨道数(此时G0轨道恰为群X的结合类,因此d+1亦为X的结合类个数,对于任意的a∈X均有aXia-1=Xi)。如果X本身就是一个交换群,那么所得到的结合方案是交换的。

2.2 有限单群与本原结合方案

代数组合的起源可以追溯到数学领域的不同分支,其中一个重要起源可以追溯到群论中舒尔在1933年关于舒尔环(Schur环) 的工作。最初Schur环是用来研究具有正规子群的本原置换群,其中大部分的结论后来被发现也适用于具有正规群作用的本原结合方案(primitive association scheme)。本原结合方案对代数组合的研究具有什么样的意义呢?类比有限单群解析本原结合方案更能贴切地展示出它在代数组合中的研究价值和核心地位。

有限群论的研究可以分为两部分：一是找出所有的有限单群,研究它们的结构;二是研究这些单群如何合成原群。如果能找到所有的有限单群,群论中的很多问题就迎刃而解了。于是,有限群论最核心的问题就是有限单群的分类。

类比利用群结构理论研究群论分类问题的方式,代数组合在没有群结构的背景下,将困难重重。但是1984年坂内英一与伊藤达郎出版的第一部代数组合专著[7]给这一问题带来了曙光。他们基于Delsarte理论,提出了P-与Q-多项式结合方案的分类问题,此后该问题被普遍认为是代数组合领域的主要研究目标之一,这项工作也被国际数学界认为是坂内英一在代数组合研究领域做出的突出贡献之一,他曾这样写道：“P-与Q-多项式结合方案看起来就像李群中的半单李群和有限群论中的有限单群一样吸引着我们。”([7],186页)

在20世纪80年代早期,坂内英一心中萦绕着一个想法：能否利用“有限单群的分类”给出群本原交换结合方案的完整列表。他相信：在代数组合的背景下,本原交换结合方案的分类应该作为重要的研究目标。这就好比我们熟知的元素周期表,元素是组成自然界物质的基本单位,因此确定出所有的元素具有重要意义。由于群可以通过单群合成,故单群类似于元素。在结合方案中,本原结合方案好比群论中的单群,但其数量庞大,以至于对它们的完整分类是非常困难的。一个群结合方案的本原性与该群的单性等价,因此研究本原结合方案是很重要的。就像任何有限群都是由一系列单群得到的一样,任何(交换的) 结合方案都是由一系列本原结合方案得到的。

正如坂内英一坚信的那样,类似单群在群论中的角色,在代数组合的研究过程中锁定了将本原结合方案看作构成结合方案的基本对象(利用任何有限单群构造一个本原交换结合方案),代数组合领域的学者们希望能对本原结合方案的结构进行代数分类和组合分类,这样可能有一天沿着代数组合的途径可以给出一种有限单群分类的替代方法。

2.3 群论与结合方案上的西罗定理

在众多有限群的构造方法中,通过元素或者子群的性质来刻画有限群的结构,一直是群论学家热衷讨论的一个活跃话题,且已经形成了一些经典的方法和结果。比如群论学家经常会借助子群来研究群的重要结构特性,包括如何通过较小的群来构造较大的群,如何剖析较大的群从而揭露蕴含在其中较小的群,这些问题都是通过“子群”来逐一进行回答的。

基于群论的思想和方法,类比到代数组合中就会发现：结合方案中的闭子集保留了类似群论中子群的一些经典的性质,因此寻找或分类已知结合方案的子方案一直是代数组合领域学者们深入分析的问题(5)“寻找或分类已知结合方案的子方案”与寻找一个“较小的结合方案”来决定给定结合方案的特征标表有关,较小的结合方案是指“顶点数少”或“类数少”,但是研究小的结合方案是一件非常困难的事情,比如完全列出顶点数不超过50的结合方案是很困难的。,进而研究是否存在结合方案(裂变方案)使得它包含已给定的子方案也是代数组合领域中的一个重要研究方向。

20世纪90年代,齐尚(P.-H.Zieschang)建立了结合方案的公理化理论,并在此基础上开始了对结合方案结构理论的系统研究,并将研究成果撰写成两本专著[22-24],引起了许多学者对结合方案结构理论研究的强烈反响。在研究过程中发现,利用有限群的结构思想,会在结合方案中收获很多的惊喜,比如将有限群中的西罗定理成功地推广到结合方案上[24],这项研究的意义在于给出了在群论之外,西罗定理的一种推广证明。

群论中西罗定理在特殊情形下回答了拉格朗日逆定理的问题(即如果n是|G|的一个因子,那么G一定有n阶子群吗?),这个结论并不成立。西罗(P.L.M.Sylow,1832—1918)首先将p阶子群的概念推广,引入了p-子群,特别是西罗p-子群的概念。所谓p-子群就是指阶数为素数幂的子群,而西罗p-子群则是指群G的最高次素数幂阶的子群,比如对于120=23×3×5阶群S5来说,西罗p-子群的阶数为8,3和5。西罗定理描述了找到哪些阶的子群一定存在,从而揭示出群G与其西罗p-子群的关系。

在群论中,西罗的三个定理间的主线是：它们都是由群的阶来决定群的结构。三个定理分别回答了西罗p-子群的存在性问题、关系问题以及数量性问题。

西罗第一定理：设G是pnm阶群,其中n≥1,p为素数,并且(p,m)=1,则对每个1≤i≤n,G均包含pi阶子群,并且G的每个pi阶子群均是某个pi+1阶子群的正规子群。

西罗第二定理：如果H是有限群G的p-子群,而P为群G的任一西罗p-子群,则存在x∈G,使得H

西罗第三定理：如果G是有限群,而p是素数,则G的西罗p-子群的个数是|G|的因子,并且具有形式kp+1(对于某个k≥0)。

由于结合方案中没有群的概念,若想将有限群上的西罗定理推广到结合方案上,首要工作是需要巧妙地利用集合的关系语言(下述xg的定义)代替群中元素的二元关系运算,从而建立类似群中元素的阶以及群的阶等相关概念,如结合方案中价的定义、p-价子集的定义等等,具体构建形式如下：

若X是有限集,G是X×X的划分,且∅∉G和1X={(x,x)|x∈X}∈G,(X,G)表示一个结合方案(简称方案)。若p是一个素数,G中的元素g称为p-价的,如果ng可以表示成p的方幂,其中ng=|xg|,∀x∈X,g∈G,xg={y∈X|(x,y)∈g};G的一个子集称为p-价的,如果它的每个元素都是p-价的;G的一个p-价子集F称为p-子集,如果nF可以表示成p的方幂。G的一个非空子集F是闭的,如果满足对于∀d,e∈F总有de⊆F。

在如上结合方案“价”(类似群中“阶”的定义)的定义框架下,第二个重要的工作在于要将有限群中西罗p-子群的定义推广到结合方案中封闭的西罗p-子集Sylp(G)上,这里Sylp(G)表示满足特定条件的由G的全体西罗p-子集构成的集合,即G的所有封闭p-子集H的集合。为了推广群中西罗第三定理,这里需要特别要求p满足不整除nG//H,其中G//H={gH|g∈G},gH={(yH,zH)|z∈yg},yH={t∈X|(y,t)∈H},yg={z∈X|(y,z)∈g}。

在综合上述两项重要工作的基础上,2002年坂内英一的学生平坂贡(M.Hirasaka)与齐尚等人在论文《有限群中西罗定理到结合方案上的推广》(AGeneralizationofSylow’sTheoremsonFiniteGroupstoAssociationSchemes)[24]中将有限群上西罗定理推广到结合方案上：

设X是有限集,G是X×X的划分,且∅∉G和1X={(x,x)|x∈X}∈G,(X,G)是有限结合方案,p是素数,P为G的一个封闭p-子集。如果G是p-价的,则有下列结论：

(1)若P∉Sylp(G),则存在G的一个封闭p-子集P′使得P⊆P′⊆NG(P)且pnP=nP′,其中NG(P)={g∈G|gPg*⊆P}。

(3)若P∈Sylp(G),令N=NG(P),则nG//N≡1(p)且nG//N≡|{gPg*|g∈G}∩Sylp(G)|(p)。

结合方案中的西罗定理与群论中的西罗定理有何联系呢?结合方案中西罗第一定理借鉴了群论中的柯西定理和正规化子,探讨了结合方案中封闭p-子集的存在性问题。结合方案中西罗第二定理讨论了结合方案中满足特定关系的封闭p-子集之间的关系,得到了类似群中的共轭关系P′=gPg*,与群论中西罗p-子群之间的共轭关系H=xPx-1异曲同工。结合方案中西罗第三定理借助了整除性质,探讨了西罗p-子集的个数问题(结合方案中没有轨道的定义)。

总之,将西罗定理从有限群推广到结合方案上,表明了结合方案可以融合某种抽象的结构理论,这些结构理论以群理论为模型展开。类似西罗定理在群论中的地位与作用,在这种推广意义下的西罗定理必然会对结合方案的结构理论研究和分类研究提供有力的工具和思想的引领。

2.4 群与结合方案的特征标理论

在数学结构方面,结合方案比有限群具有更一般的结构,这种结构不是任意的一般,而是具有类群的结合性和逆元性的结构。这使得在结合方案的研究过程中,有限群理论经常会隐式地出现。在群论中,时常能挖掘到与结合方案理论对应的相似的群理论,最典型的就是由弗罗贝尼乌斯、舒尔和伯恩赛德等人建立的有限群特征标理论。特征标理论具有怎样的研究价值呢?在群论的研究中,往往需要针对结构特征进行计算,这对刻画群是至关重要的。群的特征标表可以透视出众多群结构及群性质方面的信息,堪称群表示论最有力的工具之一,例如通过特征标表可以查出一个群的所有正规子群。

在代数组合的结构研究中,众多数学家借鉴了有限群研究中利用特征标理论研究群结构的思想和方法,利用结合方案的特征标表对结合方案的结构进行了计算研究。20世纪80年代早期,坂内英一认为对已知结合方案的参数以及特征标表的计算是可行的,于是他开始研究群本原交换结合方案的主要来源,收集已知的群本原交换结合方案以及计算它们的特征标表,因为研究特征标表的构造是系统研究这些结合方案及其分类的至关重要的第一步。随着大量成对结合方案的例子被发现,其中“较大”结合方案的特征标表在某种程度上可以被“较小”结合方案的特征标表所决定。由于代数组合的特征标理论是有限群特征标理论的自然概括,所以有限群的一些性质可以在结合方案的框架中进行解释。

此外,在代数组合中还有一些令人惊喜的发现,比如许多例子表明结合方案的特征矩阵P和Q的值都在分圆域中,但是这是否总是正确的(对有限群成立)?这个问题一直困扰着代数组合的研究者们。1980年5月,诺顿(S.P.Norton)在Oberwolfach会议上提出了这个问题。这个问题的非凡意义在于,其肯定的答案将意味着结合方案的理论可以非常类似于群论。因此,很多学者将“能否对特征标表进行分类”视为迈向“结合方案分类”的关键第一步,然而这个问题的前期未决之谜在于“一个交换结合方案的特征标表是否被包含在一个分圆域中?”尽管这项研究工作还在进展中,但是从研究的发展过程中发现,当代数组合的研究者们遇到一些关键问题或者处于迷茫的时候,会试图在群论中找到开启思想大门的钥匙。事实证明这样的做法已经取得了一些丰硕的成果。当然,新学科的兴起也势必激起对群论新视角的探究思考。

2.5 结合方案的对偶性

关于对偶性,川田在早期也证明了交换C-代数的一个对偶性,它是由非紧拓扑群理论中著名的Tannaka对偶性所引发的。川田证明的这种对偶性本质上就是交换结合方案的对偶性,并在论文[16]中完成了大量的计算,只可惜这篇论文当时并没有引起太多的关注。事实上,结合方案的代数对偶结构可以看作是舒尔环在置换群背景中的拓展[25],即有限群的不可约特征标与共轭类之间的对偶性。类似地,一般(交换)结合方案也有对偶性。在代数组合的研究中经常出现这样的情形,即用结合方案比用群论的语言描述更自然。正如1973年德尔萨特在他的博士论文中通过研究结合方案的对称性质,从代数角度在结合方案框架下定义了e-码和t-设计,其中e-码定义在P-多项式结合方案上,而t-设计定义在Q-多项式结合方案上,把Q-多项式结合方案定义为P-多项式结合方案的对偶。[20]而后德尔萨特以P-多项式结合方案和Q-多项式结合方案作为底空间,建立了编码理论和设计理论之间的对偶。凭借这种对偶性,德尔萨特将编码理论和设计理论在结合方案的框架下进行了统一研究,这项工作成为了代数组合发展史中最精彩的篇章之一。分析德尔萨特理论的成功之处,其中一个重要的原因就是他仅仅用代数的方式定义了二元概念,即在群论背景下,把群视为一个带有二元运算的集合,这是一种很好的研究方法。对于某些群,可以通过构造一些设计,使得这些设计上的自同构群恰好是满足某种研究目的的群,这比仅仅从群论角度考虑群的结构简单许多,也更为具体。从设计的角度对群论产生影响,这样的研究方式,早在马蒂厄群(Mathieu群) 上曾有过突出的表现。1861年马蒂厄(É.Mathieu,1835—1890) 构造了几个多重可迁群,特别地定义了5-可迁置换群M12和M24[26-28],并给出了它们的生成元集合。1938年维特(E.Witt,1911—1991) 构造了一个5-(12,6,1) 设计和一个5-(24,8,1) 设计,并证明它们的自同构群分别是M12和M24,于是设计的结构赋予了马蒂厄群一个很好的具体解释。在此基础之上,结合德尔萨特创立的编码和设计间的对偶理论,特别是组合t-设计(Johnson结合方案J(v,k)上的t-设计) 的自同构群将有助于发现更多的设计结构,从而助力群论思想及方法在代数组合领域的渗透和应用。

3 结 语

代数组合作为一门具有代数化思想的交叉学科,表面上看似没有群的定义、性质和结构,但是其学科体系中内蕴着强大的群论思想和结构,其中的奥妙之处值得精研深思。在罗塔、斯坦利、维兰德、川田、希格曼、坂内英一、德尔萨特等众多学者的共同努力下,促进了代数学与组合学的交叉融合,使得在代数组合四大经典问题(刻画问题、分类问题、结构问题、实现问题) 的研究中继承了群论的思想和方法,推广了群论的性质。在代数组合学科体系中,结合方案具有类群的结合性和逆元性的数学结构,因此基于结合方案的视角对代数组合中群论思想和方法进行剖析,寻本究源找到与结合方案理论对应的相似群理论,梳理出代数组合与群论的共同逻辑基础、共同概念基础和共同方法基础,进而为代数组合的发展提供价值观并指引方向。

(1)结合方案是有限集合X以及X上满足一定公理的关系集合{Ri}0≤i≤d。借助群论的思想和方法,将任意的可迁群或置换群G作用在X×X上产生的轨道记为结合类集合或结合关系集合,研究这些关系以及这些关系之间所具有的性质,并把这些性质一般化,进而推广到一般的组合结构中,这就是群论视角下结合方案概念的内涵。

(2)“一个交换结合方案的特征标表是否被包含在一个分圆域中”可以作为衡量“模仿有限群理论研究结合方案”这个策略的有效性的试金石。

(3)在结合方案中,本原结合方案好比群论中的单群,任何(交换的) 结合方案都是由一系列本原结合方案得到的。深入挖掘群本原交换结合方案以及计算它们的特征标表,是系统研究这些结合方案及其分类的至关重要的第一步。

(4)将有限群中的西罗定理推广到结合方案上,将为结合方案的结构和分类研究提供有力的工具。

(5)类似有限群的不可约特征标与共轭类之间的对偶性,代数组合中最为精彩的篇章之一是德尔萨特建立了编码理论和设计理论之间的对偶,凭借这种对偶性,将编码理论和设计理论在结合方案的框架下进行了统一研究,为现代编码理论和设计理论的研究开辟了一片新天地。

事实上,在代数组合中还有很多的“群论”思想和方法未曾一一列出,但是单从上述典型问题的剖析便可以体会到群论精髓渗透的威力。总之,代数化是20世纪数学发展的一个重要特征。随着群论被多向性地渗透与应用,其自身也在不断地从其他领域吸取新思想、新方法。因此,“交叉、融合、统一”的倾向成为了群论在20世纪发展过程中的重要特征。从数学史的角度梳理分析交叉学科的发展历程,是时代赋予数学史研究工作的新的使命,且具有极为重要的研究意义。正是由于群论与组合学家们在长期研究工作中的思维碰撞,使得很多经典的群论思想和方法得以认同、秉持、继承、丰富、发展以及传播,使得代数组合在群论辐射下的发展历程可为学科间交叉应用提供宝贵的历史经验。