基于人工神经网络算法的垃圾组分识别模型研究

陈 彧，魏 然，宋立杰，张瑞娜，周 涛，2，赵由才，2

(1. 同济大学 环境科学与工程学院，上海 200092；2.上海污染控制与生态安全研究院，上海 200092；3.上海环境卫生工程设计院有限公司，上海 200232)

前 言

近年来，中国经济高速发展，城市居民生活质量显著提高，生活垃圾的产生量亦与日俱增。据《中国城乡建设统计年鉴》显示，1979年城市生活垃圾清运量为0.25亿吨，而2018年增长至2.28亿吨。2030年中国生活垃圾产生量预测值达到4.8亿吨[1]。生活垃圾清运量的逐年增加意味着生活垃圾管理行业体量仍在增长，给后续的垃圾收运和处理处置工作造成压力。2019年7月1日，《上海市生活垃圾管理条例》开始施行，规定中明确要求建立健全生活垃圾全程分类体系。

人工智能(Artificial Intelligence，AI)是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门技术科学。在物联网和移动互联网技术迅速发展的背景下，为应对城市生活垃圾产量的增加和垃圾分类管理的新要求，生活垃圾管理系统逐渐向互联互通、智能化的“智慧环卫”的发展。机器学习(Machine Learning)是一种实现人工智能的方法，可分为监督学习、非监督学习、强化学习[2-3]三种类型，每种类型可使用一些特定算法来实现。AI技术的应用可以辅助进行生活垃圾全过程实时管理，帮助合理设计环卫管理调度，提高环卫作业质量，降低环卫运营成本，且便于进行环卫系统评估。为避免生活垃圾管理不当可能带来的一系列人居环境问题[5]，需加快落实以垃圾分类为导向的智能化生活垃圾管理系统。

因此，开展基于机器学习算法的生活垃圾组分识别，对于生活垃圾分类管理具有重要意义。如在源头垃圾投放点，利用生活垃圾组分识别技术可实现垃圾组分监控和垃圾回收价值的估测，帮助环卫管理部门收集基础数据供管理决策。本论文利用TensorFlow深度学习框架实现ANN算法，建立以光学和重量信息为基础的生活垃圾组分识别模型，对比不同模型结构、激活函数、迭代训练次数、学习率等超参数设置下模型的识别效果，分析ANN算法在此垃圾组分识别模型中的最优算法架构及实际应用可行性。

1 实验材料与方法

1.1 生活垃圾来源

试验所用的生活垃圾成分取自上海市某居民小区。在小区干垃圾收集桶中进行采样，剔除样品中除纸类和塑料以外的其他组分，得到纸类和塑料两种生活垃圾组分，静置保存于4 ℃冰箱待用。为确保试验结果的可靠性和准确性，采样后所有试验均在48 h内完成。

1.2 光学信息收集

可见光范围内的滤光片可以使工业相机清晰成像。一般人的眼睛可以感知到的可见光波长范围为400～760 nm。使用510 nm、570 nm、590 nm、650 nm四种滤光片，对光学信息的丰富度进行加强。

垃圾光学信息获取装置主要包括：固定光源、带底色标记框(PVC塑料1 m×1 m，底色白色)、色彩校正标记物、多通道工业相机、计算机、多带宽滤光片(带通510 nm、570 nm、590 nm、650 nm)、固定高度的相机三脚架所组成。四种带通的电磁波透过情况见图1所示。

图1 510nm、570nm、590nm、650 nm四种工业相机滤光片的波长-透光率图Fig.1 Wavelength-transmittance diagram of 4 industrial camera filters (510nm，570nm，590nm，650 nm)

1.3 重量信息收集

试验需要对光学采样框内的垃圾的物理组分进行统计，统计类别包括纸类和橡塑类两类。纸类包括各种废弃的纸张及纸制品。橡塑类包括各种废弃的塑料、橡胶、皮革制品。重量信息的统计流程为：1)将光学采样框中的样品取出，按照纸类和橡塑类两类进行分类；2)使用电子秤测量纸类和橡塑类的重量；3)依据重量分别计算纸类和橡塑类的组分比例以及样品的总重量并记录。

1.4 试验方法

建立模型所使用的编程语言为Python，集成开发环境为Pycharm 2018年教育版，所构建的模型使用人工神经网络(Aritificial Neural Network，ANN)算法。利用TensorFlow深度学习框架进行模型代码编写。

2 研究结果

2.1 ANN算法模型超参数设置

2.1.1 数据处理与模型架构

使用TensorFlow深度学习框架建立ANN算法结构，对所收集到的生活垃圾光学和重量信息数据进行拟合。建立一个三层ANN模型结构，结构如图2所示。输入层包含6个节点，分别代表生活垃圾重量与5张不同镜头所摄照片的RGB均值。原图像经过采样区范围截取后，图像像素尺寸为1420×1420，利用Python对所有图像进行RGB均值的读取。RGB均值的数据范围为0～255，重量数据范围为0～500 g，用所有参数除以250的标准进行统一处理可使数据之间相差范围尽可能减小。

图2 ANN算法架构图Fig.2 Algorithm architecture diagram of ANN

ANN结构中，隐藏层2层，每层包括4个节点。输出层1层，包含1个输出节点，代表纸类组分占比，另一种组分含量可以直接由纸类含量计算出，故使用1个输出节点与使用2个输出节点的效果相同。

ReLU函数、Tanh函数、Sigmoid函数是三种常见的非线性激活函数。为保证输出层中输出的数据范围处于0～1的范围内，设定输出层的激活函数使用Sigmoid函数。在三层神经网络模型的结构基础上，对隐藏层的激活函数进行修改，共建立四种模型，分别编号为A1、A2、A3、A4号模型，其各层级中激活函数的设置如表1所示。

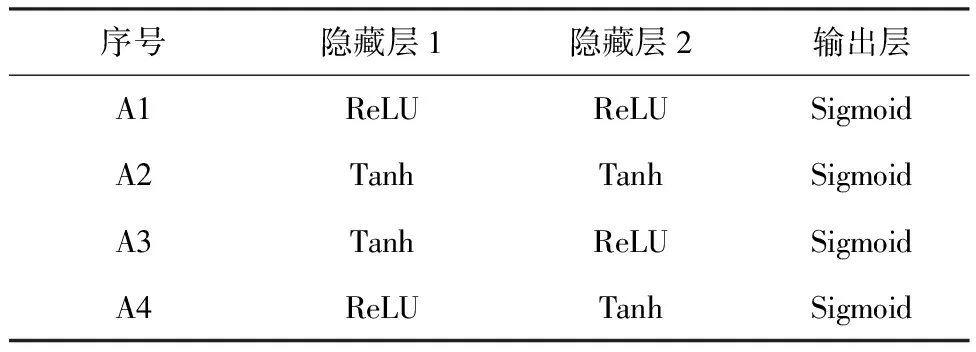
表1 A1-4号模型的激活函数构成Tab.1 Composition of A1-4 Models’ Activation Function

2.1.2 Adam优化算法

ANN算法需要利用现有数据更新每层结构中的权重和偏置量参数。最经典的参数优化算法为梯度下降优化算法(Gradient Descent Optimization)[6]。梯度下降算法的计算过程即计算目标函数对于参数的梯度，将参数沿着梯度相反的方向移动一个步长，以期实现目标函数值的下降，获得目标函数最小时的参数配置。Adam优化算法是由Kingma等人在2015年提出的一种新的参数优化算法。结合了冲量梯度下降算法的冲量项应用和RMSProp优化算法的学习速率自适应。算法中的主要运算过程见式(1)～(5)所示。

mt=β1mt+(1-β1)gt

(1)

(2)

(3)

(4)

(5)

2.2 模型训练与性能分析

2.2.1 学习率与迭代次数调试

学习率(Learning Rate)被机器学习领域最重要的超参数之一，对模型是否能得到有效训练至关重要[7]。以A1模型为例，详细分析学习率和迭代次数调整对模型性能的影响。

一般学习率取作较小的参数值，通过数量级的改变来进行调试。当学习速率为0.1时，迭代次数分别为40次和80次时，迭代次数与损失函数值的关系图如图3所示。

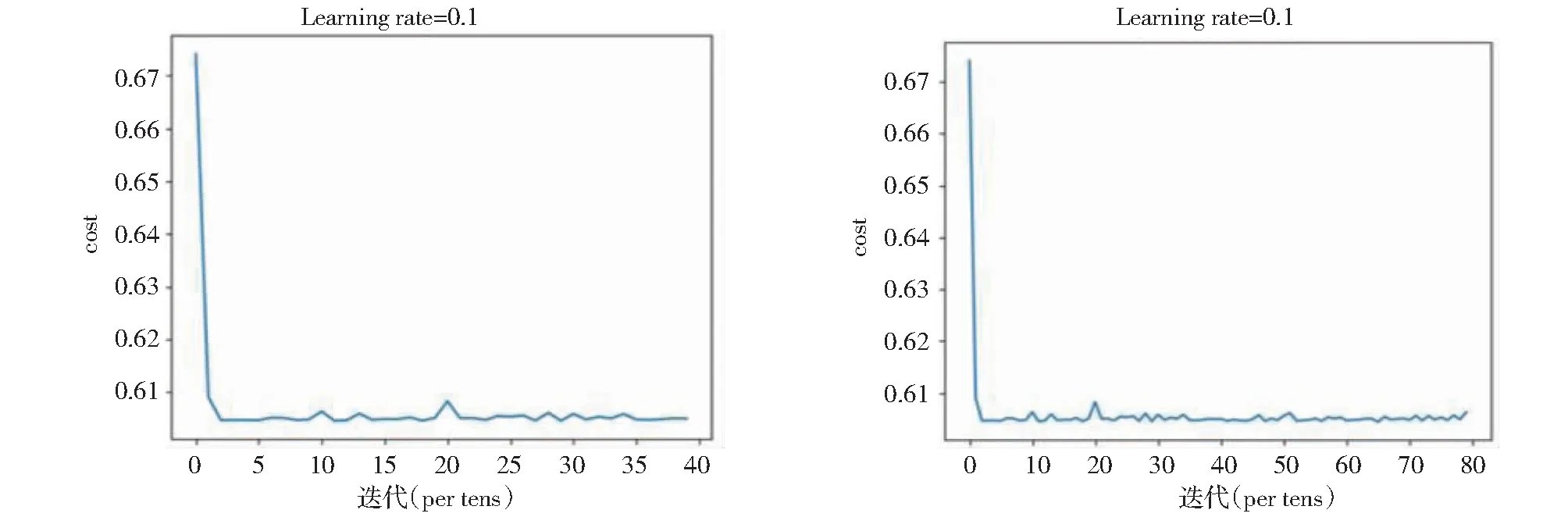
图3 学习速率为0.1时，迭代次数(40次与80次)与损失函数值的关系图Fig.3 Relationship of iterations (40 times and 80 times)and loss function value (learning rate = 0.1)

输出结果表明经过在学习速率为0.1，一批训练量为5个样本量，迭代40次，可以观察到成本函数随着迭代次数增加呈现下降趋势和明显收敛。此时预测结果无法呈现有效的回归输出。可能是由于学习速率太大，导致损失函数无法进一步优化缩小。且出现了明显的损失函数振荡，即算法训练时步长太大，导致参数优化时直接越过最优点到达另一端。

当学习速率为0.01时，迭代次数分别为40次和80次时，迭代次数与损失函数值的关系图如图4所示。

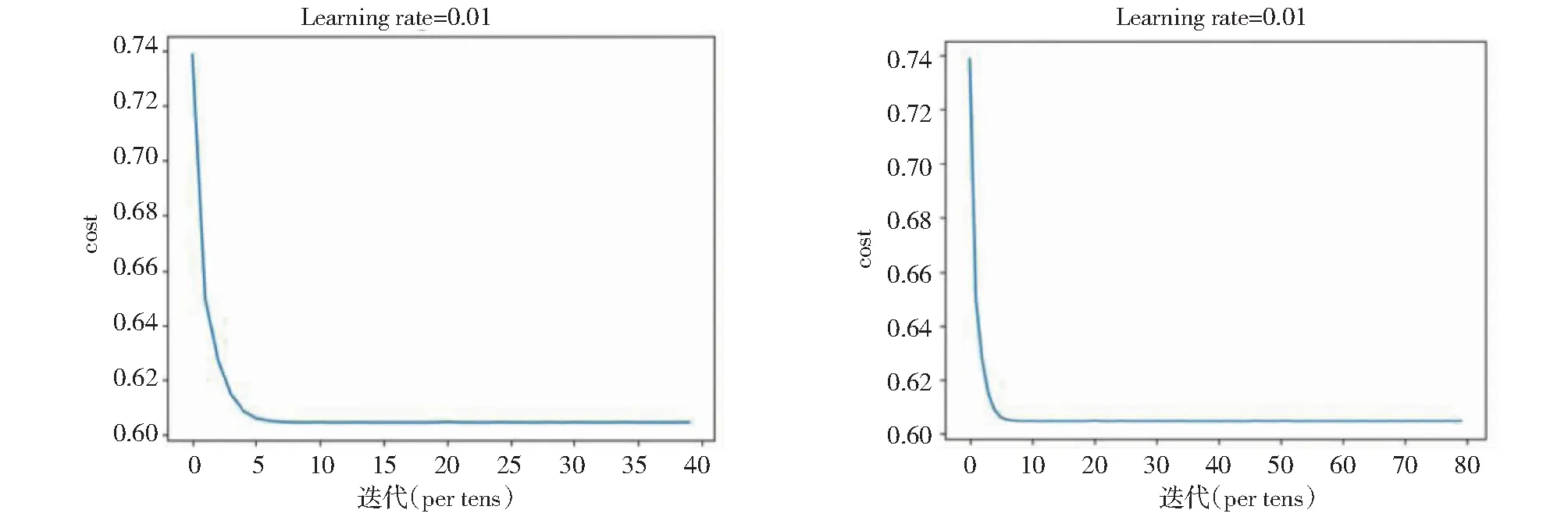
图4 学习速率为0.01时，迭代次数(40次与80次)与损失函数值的关系图Fig.4 Relationship of iterations (40 times and 80 times)and loss function value (learning rate = 0.01)

输出结果表明经过在学习速率为0.01，一开始可以观察到成本函数随着迭代次数增加呈现下降趋势和明显收敛。但数次迭代后，虽没有出现损失函数振荡现象，但参数停止更新，损失函数值不再下降，可能是模型陷入局部最优解，导致损失函数无法进一步优化缩小。

当学习速率为0.001时，迭代次数分别为40次和80次时，迭代次数与损失函数值的关系图如如图5所示。

图5 学习速率为0.001时，迭代次数(40次与80次)与损失函数值的关系图Fig.5 Relationship of iterations (40 times and 80 times)and loss function value (learning rate = 0.001)

当学习速率为0.001，迭代40次和80次时，可以观察到损失函数随着迭代次数的增加呈现下降趋势并未出现收敛。这可能是由于迭代次数不够，参数并未更新至最优位置。当迭代次数为80次时，预测误差在±24.15%以内。

调整迭代次数至200次和400次时，可以发现曲线在200次以内也并未出现收敛趋势(如图6所示)，数据的最终预测误差在±3.62%以内。进一步提升迭代次数至400次，可以观察到损失函数在迭代约200次时开始呈现收敛趋势，函数值不再出现明显下降，而迭代400次的模型最终预测误差在±5.36%以内。误差比迭代200次时的模型要高。这可能是由于模型出现了过拟合现象(Overfitting)，出现过拟合现象的常见原因[8]有：(1)由于选取特征或样本不够具有全局代表性或样本数量少，无法拟合出较有代表性的模型；(2)样本噪音干扰过大，扰乱了参数正常拟合；(3)权值学习迭代次数过多，拟合了训练数据中的噪声和训练样例中没有代表性的特征等。

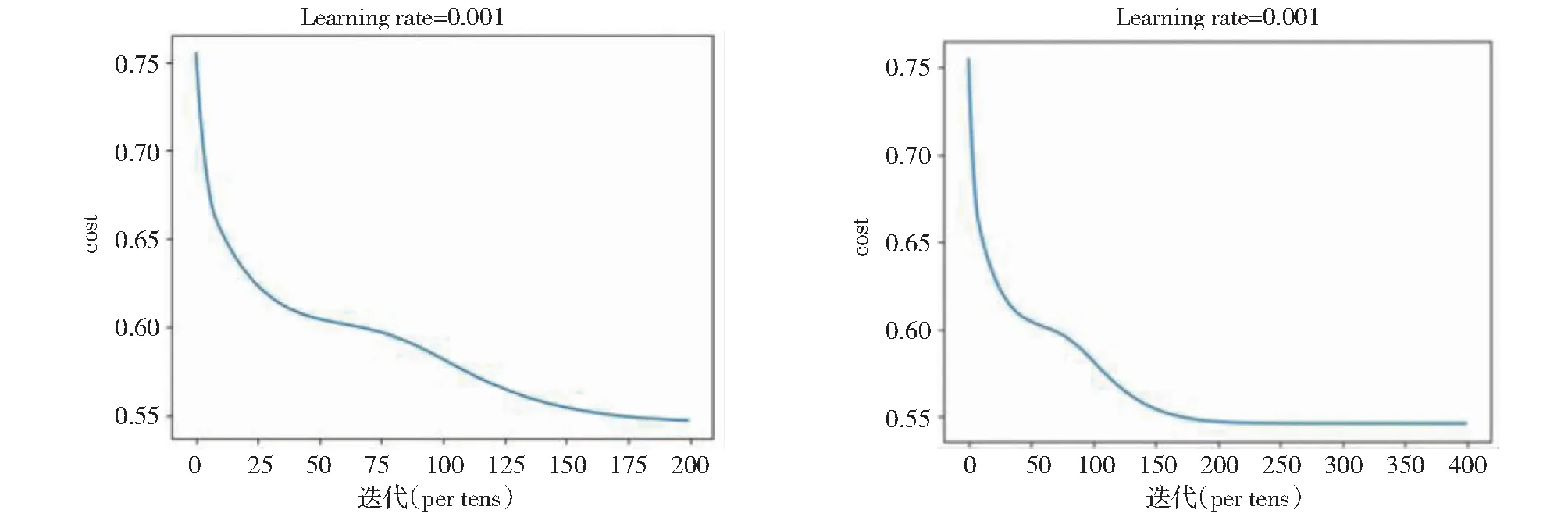
图6 学习速率为0.001时，迭代次数(200次与400次)与损失函数值的关系图Fig.6 Relationship of iterations (200 times and 400 times)and loss function value (learning rate = 0.001)

此处可能是由于学习迭代次数过多，导致参数自初步收敛后的更新方向偏向于拟合了训练数据中的噪声所导致的过拟合现象。但选取0.001作为学习率时，模型的整体表现优于0.1和0.01。参数得到了有效的更新。故而确定学习率的数量级基本在10-3。当学习速率为0.002，迭代80、200、400次时，损失函数在约125次时呈现出明显收敛趋势。三种情况下最终预测误差在分别为±9.28%、±4.71%、±5.68%。同样出现了当权值更新迭代次数过多时，误差反而变大的情况。尝试过多种学习速率与迭代次数的组合后，最终得到误差率最低的组合为学习率为0.001，迭代次数为200次，数据的预测误差在±3.62%以内。

2.2.2 模型性能分析

A1模型在尝试调试学习率和权值更新次数后，可知学习率为0.001，迭代次数为200次时，A1模型数据的预测误差在±3.62%以内。具体的预测误差表见表2所示。

表2 A1模型的预测误差表Tab.2 Prediction error of A1 Model (%)

对A2模型进行学习率和权值更新次数的调试后发现，当学习率为0.1时，A2模型的在权值更新次数达到300次后，出现无法继续正常更新参数使损失函数变小的情况，且在300次以前的模型拟合效果较为普通。当学习率为0.01和0.001时，A2模型的预测误差见表3所示。

A2模型在学习率为0.01时的训练效果较好，在200次后预测误差都达到了1%以内的水平。0.001的学习率对A2模型的参数更新过程来说可能步长较短，故而参数优化无法得到快速收敛。

A3模型在学习率为0.1或0.01时，模型均无法得到正常训练，而在学习率为0.001时，效果表现普通，最优参数组合为权值更新次数2000次时，预测误差才可达到1%以内。A3模型如果达到较为稳定的预测效果，必须得到大量多次训练。当学习率为0.001时，A3模型的预测误差见表4所示。

表4 A3模型的预测误差表Tab.4 Prediction error of A3 Model (%)

A4模型在学习率为0.1时，进行权值更新出现了剧烈的损失函数振荡现象。而在学习率为0.01和0.001时，模型表现都较好。当学习率为0.01时，经过200次权值更新后，预测误差达到1%以内，并在随后的迭代中，预测误差呈现出稳定下降的趋势。A4模型的预测误差见表5所示。

表5 A4模型的预测误差表Tab.5 Prediction error of A4 Model (%)

综合比较A1、A2、A3、A4模型的效果，可以得出A2模型和A4模型在学习率为0.01时，经过200次训练后都呈现除了较好的拟合现象。预测误差远低于其他模型。进一步比较预测误差随迭代次数的变化可以发现，A4模型随着训练迭代次数的增加，预测误差呈现稳定的减小趋势，而A2模型则在权值更新多次后出现预测误差振荡的现象，稳定性不如A4模型。

由此得出结论，在现有数据量的拟合中，三层神经网络架构足够进行数据的拟合，使用A4模型，即隐藏层第一层、第二层、输出层的激活函数分别为ReLU函数、Tanh函数和Sigmoid函数的结构，可以在学习率为0.01的情况下，使模型得到快速有效的训练，最终达到的预测误差可以稳定的保持在±1%以内。

3 结 论

(1)利用三层ANN算法结构进行建模，Adam优化算法优化参数。隐藏层数为2，每层包括4个节点。输出层包括1个节点，代表纸类的含量。根据每层激活函数的不同建立四种模型。可以建立性能优秀的垃圾组分回归模型。

(2)使用0.001作为学习率时，可以得到较好的拟合效果。对比0.001和0.002作为学习率时，迭代次数分别为80、200、400时，可知迭代次数过多，模型出现过拟合现象。最佳条件为使用0.001作为学习率，迭代次数为200时，得到数据的最终预测误差在±3.62%以内，可以达到较为稳定的预测效果。

(3)对比A1至A4四种模型，使用A4模型，即隐藏层第一层、第二层、输出层的激活函数分别为ReLU函数、Tanh函数和Sigmoid函数的结构，可以在学习率为0.01的情况下，使模型得到快速有效的训练，最终达到的预测误差可以稳定的保持在±1%以内，为四种模型中预测误差最低的模型结构。