改进的蒸汽吞吐渗流-地质力学耦合模型

JAMALOEI Benyamin Yadali

（墨菲石油公司，卡尔加里 T2N 1N4，加拿大）

0 引言

Seal Lake 稠油油田位于加拿大阿尔伯塔西北部的Peace River 油砂区，原油相对密度为0.99～1.03，黏度10 000～100 000 mPa·s。由于该地区原油黏度高，不宜长期采用一次采油方式或化学驱、气驱等非热采工艺进行开采[1-2]，应选择热采技术如蒸汽驱提高采收率技术，包括垂向蒸汽驱、趾端到跟端蒸汽驱[3-4]和蒸汽吞吐。然而Seal Lake 油田存在底水、稠油几乎不流动，部分热采工艺（如垂向蒸汽驱）的实施难度较大[5-8]。Seal Lake 油田蒸汽吞吐项目区块位于油田西北部[9]，该区块原油黏度极高、原生水流动性差，导致初始注汽能力及原油产能极低。蒸汽吞吐过程中，通过注入高压蒸汽使地层破裂、局部产生裂缝，并导致大范围地层的孔隙体积增大及地层变形。其中，地层变形包括注汽阶段的地层膨胀以及后期焖井和生产阶段的再压实。现场观测证实注汽过程中地层产生了明显膨胀：注汽强度大于基于原始储集层物性推测的强度；注汽过程引起的地表隆起幅度远大于地层热膨胀或拉伸破坏可能导致的隆起幅度。地层膨胀产生复杂的地质力学行为，决定了蒸汽初始流动路径，并在蒸汽吞吐期间提供驱油能量。因此，为了合理模拟蒸汽吞吐过程中的热-力学响应，必须在数值模拟器中描述这些现象。

20 世纪60—70 年代，建立了模拟蒸汽吞吐的基础二维解析模型[10-13]。20 世纪80 年代，提出了更复杂的二维模型，考虑了饱和滞后效应、压力和温度的周期变化对相对渗透率的影响[14-15]，以及人工裂缝、砂体变形和微通道[16-20]的影响。20 世纪90 年代，实现了储集层-地质力学三维耦合模型的构建，考虑了膨胀-再压实、地层破裂、注蒸汽诱发的剪切破坏和人工裂缝引起的孔隙体积和渗透率变化[21-27]。21 世纪初，地质力学-地球物理耦合模型主要用于预测由地层加热、孔隙压力升高、地面斜坡反转引起的地表隆起[28]，进而计算储集层体积变形量[29-30]。部分学者基于储集层-地质力学耦合建模研究了蒸汽吞吐早期的蒸汽驱压裂效果和地层膨胀-再压实效应[31-32]。

以往研究指出，地表隆起、蒸汽诱发的剪切破坏和拉伸破坏、孔隙变形和相对渗透率变化是蒸汽吞吐过程中地层膨胀和再压实阶段的主要特征。这些研究一致认为，采用合理的岩石压缩系数和裂缝长度难以模拟得到现场的高注汽能力。因而，多数研究采用高岩石压缩系数（海绵状岩石法）或长裂缝模型以再现油田现场的高注汽能力：前者即海绵状岩石法预测结果显示注入压力持续上升，但在实际注汽过程中，注入早期压力先上升，而后趋于平稳；后者采用长裂缝模型并不合理，因为在焖井和生产（再压实）阶段，垂向净应力的增大导致部分未支撑裂缝闭合。

本文基于地质力学模型，提出了改进的渗流-地质力学迭代耦合模型。改进模型能够模拟多种情况下（颗粒迁移、结垢、沉淀、流体滞留吸附等）储集层孔隙体积变化和各网格块每个方向渗透率的变化，校正由于地层膨胀-再压实阶段压缩系数异常而产生的注汽压力和注汽量误差。由于地质力学模型能够模拟储集层局部和整体变形，因而改进的耦合模型可以对实测注入压力进行更有效的历史拟合。此外，该模型还可以采用实验室测定的相对渗透率数据，并对油田的油水产量进行历史拟合。本文利用拉丁超立方体设计和响应面法，通过历史拟合结果分析、敏感性分析和不确定性评价，定量分析地层破裂压力、最大注入压力、膨胀压力、再压实压力、膨胀阶段岩石压缩系数、初始孔隙度和膨胀导致的最大孔隙度的影响，研究膨胀-再压实模型参数对蒸汽吞吐效果的影响。

1 渗流-地质力学耦合模型

1.1 渗流模型

油相和气相中i组分的质量平衡方程如（1）—（3）式所示，包括岩石相和流体相中i组分的累计项，以及l相中i组分的对流、弥散和分子扩散项：

Seal Lake 油藏模型的储集层原始压力为4.5 MPa，泡点压力为3.3 MPa。建立笛卡尔网格，角点网格数超过5×106个。模型的有效储集层厚度为19～25 m，水平渗透率为0.05～2.40 μm2，孔隙度为20%～29%，平均水平渗透率和垂向渗透率分别为1.45 μm2和0.73 μm2。模型中采用20 ℃和220 ℃下实验测得的两相相对渗透率曲线[33]，油气水三相相对渗透率曲线基于两相相对渗透率曲线利用Stone 模型Ⅱ[34-35]计算得到。其中，三相系统中的水相相对渗透率与油水两相体系中的水相相对渗透率相等，三相系统中的气相相对渗透率与气液体系中的气相相对渗透率相等。当液相的含水饱和度为临界值Swc[36]时，三相系统中油相相对渗透率由下式计算：

针对不同饱和条件，为了保证Kro=Krow（Sg=0）且Kro=Krog（Sw=Swc），令Krocw=Krow（Sw=Swc）=Krog（Sg=0）。另外，利用实验室测量的两相相对渗透率数据，模型可以考虑高温下界面张力降低对相对渗透率的影响[37-38]。

在流体模型中，地层体积系数为1.02 m3/m3，原始溶解气油比为7 m3/m3，储集层温度为20 ℃时，原油相对密度设为1.01。根据岩心数据和测井数据，模型中含油饱和度设为52%～83%。在Seal Lake 油田蒸汽吞吐项目区块，油层顶部和底部的原油黏度分别为14 300 mPa·s 和620 070 mPa·s，可以通过改变重油、溶解气和轻质油3 种原油拟组分的摩尔分数，建立原油黏度梯度。因此，流体模型包含水组分和重油、溶解气、轻质油3 种原油拟组分，用i标识流体组分，i=1代表水组分，i=2 代表重油组分，i=3 代表溶解气组分，i=4 代表轻质油组分。流体模型中采用非线性混合规则来模拟Seal Lake 原油黏度梯度（可溶气组分变化对μo产生影响）：

μoi可通过实验或相关性分析确定。此外，不同温度T时的μoi不同，可以采用（6）式利用插值法或外推法确定：

油相物质的量浓度关系式如下：

流体模型中基于K'值概念的多相平衡模型为：

当储集层压力降至泡点压力pb时，开始形成气相，此时，气相摩尔分数的约束条件如下：

由于水（i=1）和重油、轻质油（i=2 及i=4）组分没有明显蒸发，则y1=y2=y4=0，1K'=K2'=K4'=0。因此，y3=1，K3'z3=1，则K3'（pb）=1/z3随p变化：

1.2 地质力学模型

本文提出的改进地质力学模型将海绵状岩石模型和Beattie 等[21]建立的膨胀-再压实模型结合，在渗流-地质力学耦合模型中设定最大孔隙度和最大压缩系数。最大孔隙度限制了地层膨胀程度；压缩系数超过最大值时定义为异常值，由此避免网格压力错误。该处理方法对Seal Lake 油田蒸汽吞吐注采量和注入井井底压力模拟计算非常关键。

在Beattie 等提出的原始膨胀-再压实模型中，网格孔隙度随压力变化[21]（见图1）：

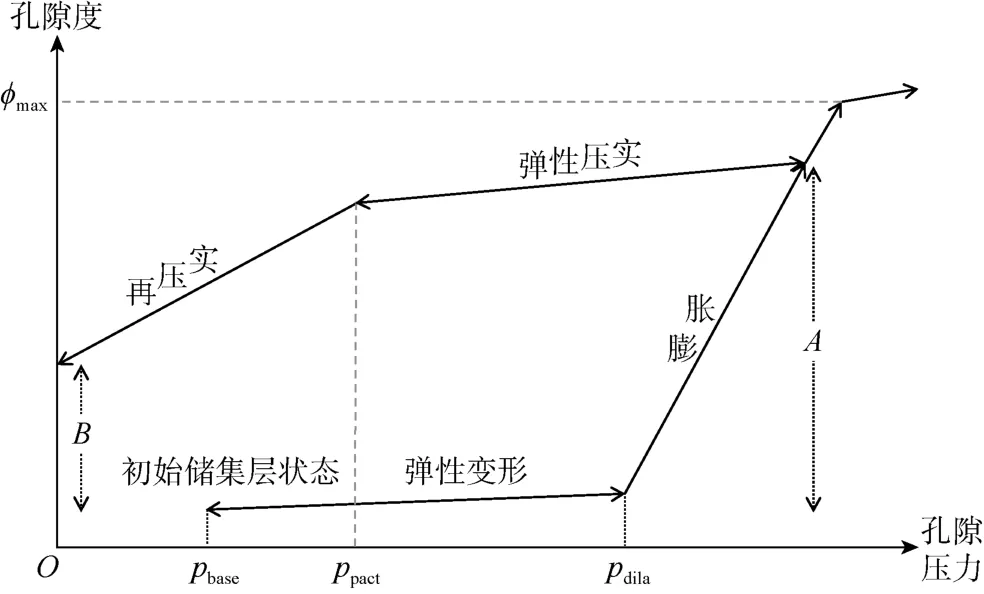
图1 蒸汽吞吐过程的地层膨胀-再压实模型[21]

由图1 所示，随着注汽量增加，压力由初始状态压力（pbase）开始上升，地层发生弹性变形。当压力超过膨胀压力（pdila）时，进入不可逆的非弹性膨胀阶段，直至孔隙度达到最大值。如果在达到最大孔隙度之前，压力下降，地层进入弹性压实阶段（双箭头表示弹性变形）。压力降至再压实压力（ppact）以下时发生再压实作用。再压实曲线斜率根据网格的膨胀历史和残余膨胀分数（fr）确定：

Beattie 等[21]考虑热效应对网格孔隙体积的影响，将（11）式修正为：

其中，热膨胀系数γT为孔隙体积热膨胀系数γTpor，膨胀阶段取热膨胀系数γTd，压实阶段取热膨胀系数γTppac。由于温度对网格孔隙度的影响远小于压力，则孔隙体积膨胀-再压实主要受压力控制。

另外，在某些地质力学和岩石物理模拟中，膨胀过程中压缩系数异常高将导致部分网格压力大幅波动，此时原始膨胀-再压实模型[21]模拟器会发出警告，甚至提前终止模拟。本研究利用海绵状岩石模型，设定最大压缩系数，从而校正可能存在的迭代错误：

本研究还考虑了网格各向渗透率随压力和温度的变化，表达式如下：

固相组分（焦炭、微粒、沉淀、结垢、吸附/滞留流体组分）含量的变化对网格渗透率具有明显影响，因此，当固相成分增加导致孔隙度和渗透率降低时，采用（18）—（21）式计算网格各方向渗透率的变化：

基于原始膨胀-再压实模型[21]（（11）—（13）式），结合本研究提出的改进（（14）—（21）式），得到改进的地质力学模型，可考虑压力和温度对网格孔隙体积和渗透率的影响。利用油藏模拟界面将地质力学模型与渗流方程（（1）—（10）式）进行热力学耦合，得到渗流-地质力学耦合模型。

2 结果与讨论

对Seal Lake 油田蒸汽吞吐生产数据进行历史拟合，从而验证改进模型的有效性。

2.1 单井蒸汽吞吐历史拟合

蒸汽吞吐改进模型主要基于两种增大孔隙度的机理来描述地表隆起和高注汽强度。①油砂具有非线性压缩性，随着有效应力趋于零，压缩系数显著增大。②地应力存在各向异性时，若有效应力过低，地层会发生剪切破坏，孔隙压力增大引起的剪切破坏会导致孔隙系统发生膨胀。当蒸汽注入压缩性较差的储集层时，孔隙压力增大，有效应力减小；此时地层压缩系数增加约2个数量级，可能引发剪切破坏。这两种现象导致地层膨胀，孔隙度和渗透率迅速增加，从而大幅提高注汽强度，之后注入压力缓慢增加。该膨胀作用主要表现为注入位置上方的地表隆起。对这些现象进行模拟时，需设特定膨胀压力：低于该压力，地层表现为弹性变形，采用较低压缩系数；高于该压力，采用较高压缩系数，使孔隙度随压力显著增大。此外，还要确定最大孔隙度：高于最大孔隙度时，不会发生进一步膨胀，压缩系数恢复到较小值。通过历史拟合，确定改进地质力学模型中的最大孔隙度为36%；膨胀-再压实模型得到的膨胀后最大压缩系数为4.8×10-8Pa-1，海绵状岩石模型得到的最大压缩系数为7.1×10-7Pa-1。

如图2 和图3 所示，改进模型提高了Seal Lake 油田蒸汽吞吐产水量、产液量、注入压力、注入蒸汽冷水当量历史拟合的准确性。新模型对产液量和产水量的历史拟合得到了明显的改进，而传统海绵状岩石模型整体高估了产液量、产水量和注汽量（见图2）。同时，与海绵状岩石法预测蒸汽吞吐过程中注入压力随时间逐渐增加相比，改进模型的压力预测结果显示井底压力先上升后趋于平稳（见图3），符合实际蒸汽吞吐开采早期特征。

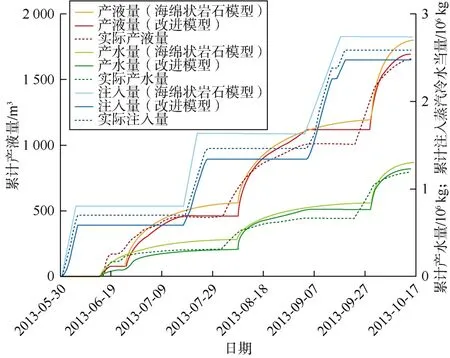
图2 产液量、产水量和注入蒸汽冷水当量的历史拟合结果

图3 注入井井底压力历史拟合

2.2 敏感性分析与不确定性评价

将破裂压力和最大井底压力分别设定为13.0 MPa和12.4 MPa，对改进的地质力学模型进行敏感性分析。根据测井资料和岩心分析数据，模型初始孔隙度分布存在非均质性，设定由于地层膨胀达到的最大孔隙度为36%。设置地质力学参数范围并评价其影响程度，其中膨胀压力为8～10 MPa，再压实压力为5～7 MPa，膨胀后岩石压缩系数为9.6×10-9～4.8×10-8Pa-1。

采用响应面法进行敏感性分析和不确定性评价。采用拉丁超立方法设计实验以同时调整多个参数[33]，导出模拟结果，以拟合多项式响应面。通过建立输入变量xj'与响应变量y'之间的数学关系，用响应面代替渗流-地质力学迭代耦合模型，该方法快速且可靠。响应面法采用以下多项式方程拟合响应面与模拟变量的函数关系。

线性模型：

二次模型：

交互模型：

其中，“交互模型”用以表征多变量（hx'，xj' ）对响应变量y'的综合影响。

表1 和表2 总结了3 个模型中不同岩石膨胀-再压实参数对Seal Lake 油田蒸汽吞吐效果的影响，可见，再压实压力对注汽量和产水量的影响最显著。此外，线性模型和二次模型中，岩石压缩系数和再压实压力都与注汽量和油水产量正相关，膨胀压力与注汽量和油水产量负相关。

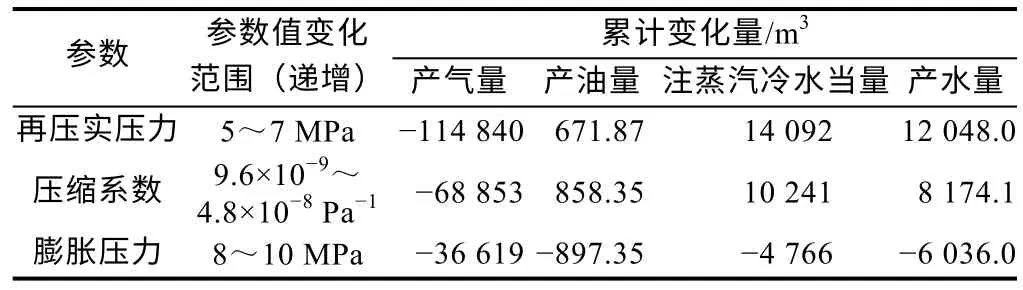
表1 线性模型中不同岩石膨胀-再压实参数对蒸汽吞吐效果的影响

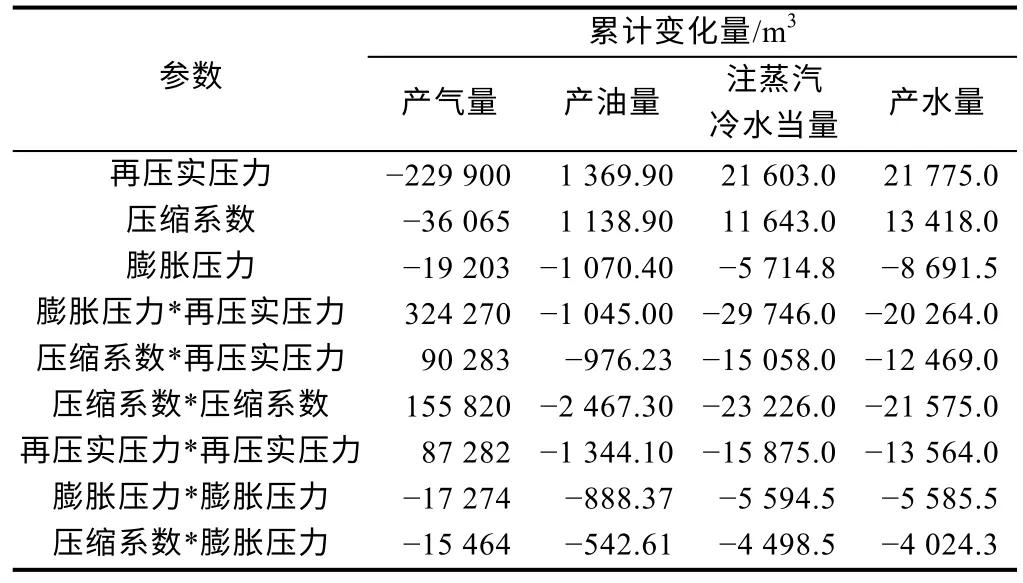
表2 二次模型及交互模型中不同岩石膨胀-再压实参数对蒸汽吞吐效果的影响

在线性模型中（见表1），膨胀压力对产油量的影响最明显：随着膨胀压力的升高，最终产油量下降，归因于膨胀压力上升导致的注汽量快速下降。随压缩系数增大累计产油量明显增加。另外，再压实压力与产油量正相关，但相比压缩系数，影响程度较弱。因此，适当增大压缩系数对增大产油量的影响最大。

在二次模型中（见表2），再压实压力对注汽量和油水产量的影响最明显，随着再压实压力的升高，注汽量和油水产量增加。压缩系数对油水产量和注汽量均产生正向影响，但影响小于再压实压力。利用二次模型及交互模型还可以研究地质力学变量之间交互作用的影响，膨胀压力、再压实压力和海绵状岩石压缩系数之间的6 种交互作用，均对累计油水产量和注汽量产生负向影响。海绵状岩石压缩系数的二次交互作用（压缩系数*压缩系数）是最明显的交互作用因子，对累计油水产量的不利影响最大。

结合拉丁超立方体设计和响应面法，分别绘制产气量、产油量、产水量、注汽量的响应面曲线。响应面曲线可以作为代理模型，用于量化模型输出变量（油气水产量和注汽量）的不确定性。采用95%置信曲线对模型输出结果进行筛选。如图4—图7 所示，响应面法预测的蒸汽吞吐输出结果中少数数据与模拟结果的误差超出了95%置信曲线的可接受范围。因此，该代理模型输出结果在预测模拟结果时产生的不确定性处于可接受范围内，可以采用该代理模型代替渗流-地质力学耦合模型进行蒸汽吞吐膨胀-再压实效应的敏感性研究。

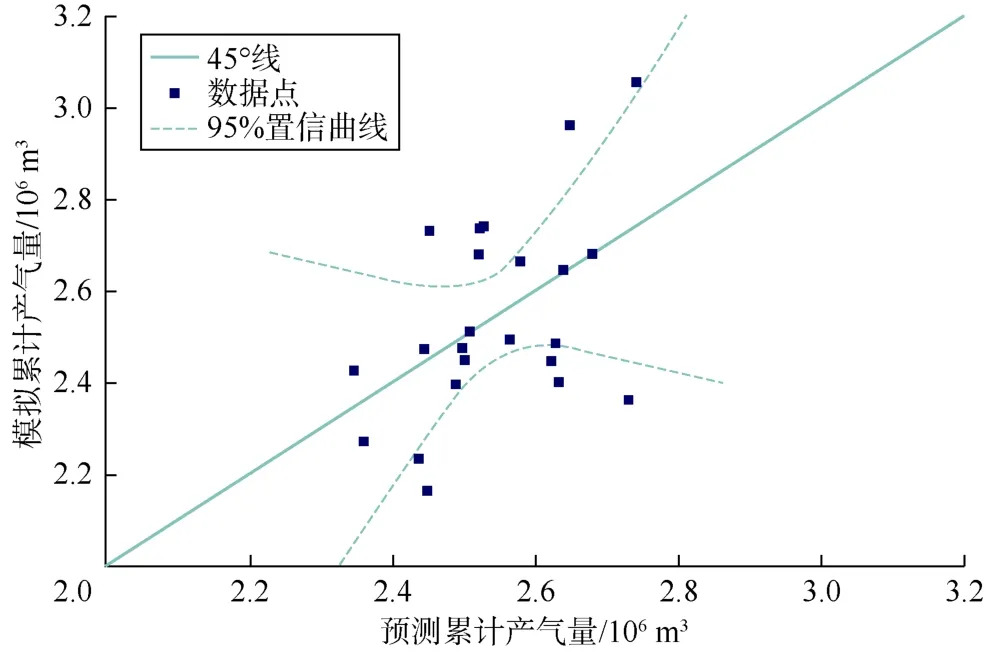
图4 产气量的响应面曲线

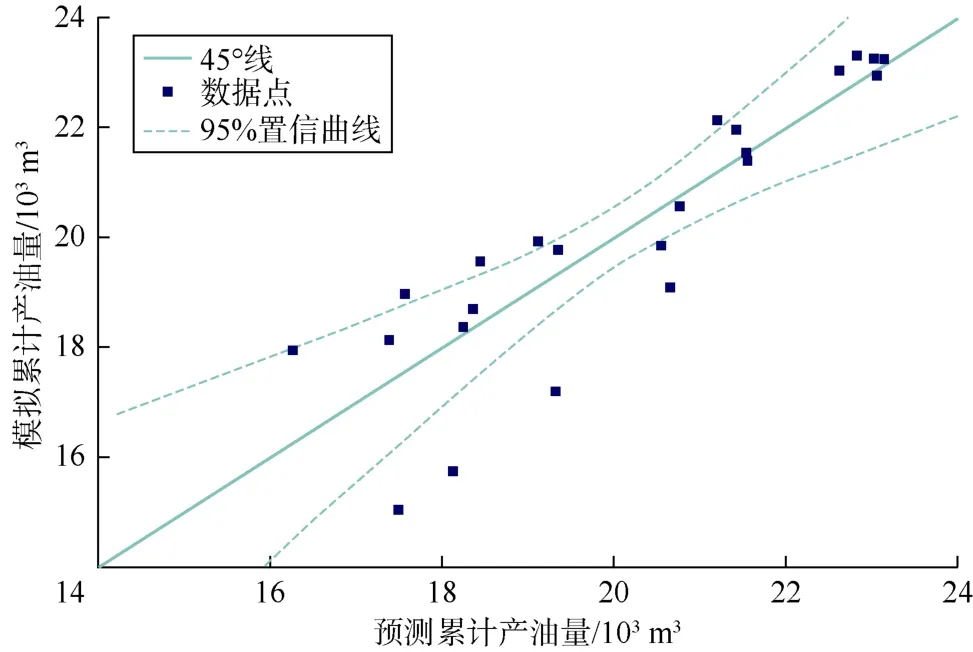
图5 产油量的响应面曲线

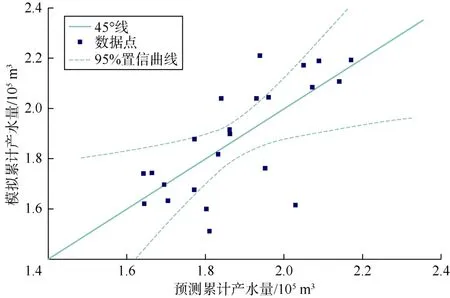
图6 产水量的响应面曲线

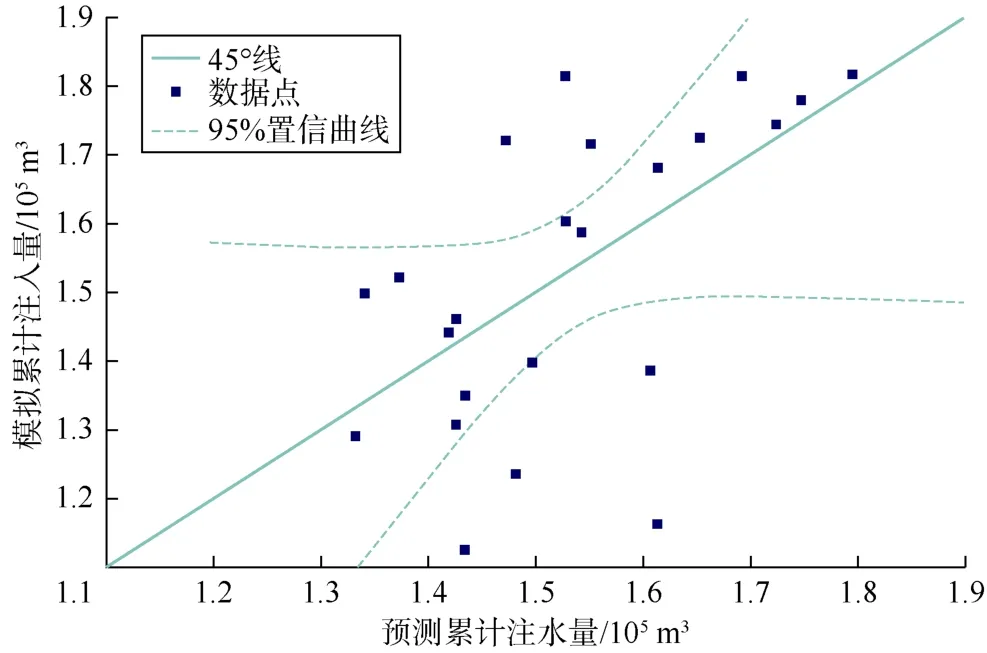
图7 注入蒸汽冷水当量的响应面曲线

3 结论

基于原始膨胀-再压实模型和海绵状岩石法，考虑压力和温度对孔隙体积和渗透率的影响，与渗流方程进行热力学耦合，形成改进的渗流-地质力学耦合模型。改进的模型能够模拟多种情况下（颗粒迁移、结垢、沉淀、流体滞留吸附等）储集层孔隙体积变化和网格各向渗透率变化，校正由于地层膨胀-再压实阶段压缩系数异常而产生的注汽压力和注汽量误差；可以更准确地实现注汽压力、注汽量及油水产量的历史拟合。

将改进模型与响应面法和拉丁超立方体设计相结合，可进行敏感性分析和不确定性评价。在线性模型和二次模型中，再压实压力的升高对注汽量和产水量的增加影响最明显，岩石压缩系数和再压实压力都与注汽量和油水产量正相关，而膨胀压力与注汽量和油水产量负相关。线性模型中，膨胀压力对累计产油量的影响最明显且负相关，压缩系数和再压实压力与累计产油量正相关，其中压缩系数对提高产油量的影响更显著。二次模型中，再压实压力对累计油水产量和注汽量影响最明显且正相关。膨胀压力、再压实压力与海绵状岩石压缩系数之间的交互作用对累计油水产量和累计注汽量均具有负面影响。

符号注释：

ai——回归法得到的黏度相关系数，Pa·s；A，B——膨胀结束（或弹性压实刚开始）和再压实结束时的孔隙度变化；bi——回归法得到的黏度相关常数，K；cg,ST，co,ST——pref、Tref条件下气相、油相物质的量浓度，mol/m3；co(p,T,xi)——p、T、xi条件下油相物质的量浓度，mol/m3；coi,ST——pref、Tref条件下油相中i组分的物质的量浓度，mol/m3；Coi——i组分压缩系数，Pa-1；Cp——孔隙压缩系数，Pa-1；Cpd——膨胀过程的孔隙压缩系数，Pa-1；Cp,ref，Cp,max——参考孔隙压缩系数及最大孔隙压缩系数，Pa-1；d0，dj，dhj，djj——多项式方程拟合常数，h、j取1～N且h＜j；Dil——l相中i组分的扩散系数，m2/s；fr——残余膨胀分数；g——重力加速度，m/s2；i——组分编号，i=1 代表水组分，i=2 代表重油组分，i=3代表溶解气组分，i=4 代表轻质油组分；kil——l相中i组分的弥散系数，m2/s；K——地层渗透率张量，m2；Krg——三相系统中的气相相对渗透率，无因次；Krl——l相的相对渗透率，无因次；Kro——三相系统中的油相相对渗透率，无因次；Krocw——束缚水饱和度对应的油相相对渗透率，无因次；Krog——油气系统中的油相相对渗透率，无因次；Krow——油水系统中的油相相对渗透率，无因次；Krw——三相系统中的水相相对渗透率，无因次；Kx，Ky，Kz——x、y、z方向的网格渗透率，m2；K'i——i组分的K'值；l——相编号；m，n，c——通过岩心分析、岩石物理测井或模拟测试得到的系数；M2——重油摩尔质量，kg/mol；M3——溶解气摩尔质量，kg/mol；N——多项式方程拟合项或常数的最大数量；Nc——组分的数量；Np——相的数量；p——压力，Pa；pb——泡点压力，Pa；pbase——初始状态压力，Pa；pdila——膨胀压力，Pa；pl——l相的压力，Pa；ppact——再压实压力，Pa；pref——参考压力，Pa；ri——源汇项，i组分注入或产出量，kg/（m3·s）；Rs（p）——压力p对应的溶解气油比，m3/m3；Sg——含气饱和度，%；Sl——l相饱和度，%；Sw——含水饱和度，%；Swc——临界含水饱和度，%；t——时间，s；T——绝对温度，K；Tref——参考温度，K；ul——l相达西流动速度，m/s；wil——l相中i组分的质量分数，%；wis——基质表面沉淀的i组分质量分数，%；xi——重油、轻质油及溶解气混合物中i组分的摩尔分数，%；x'j——响应面法输入变量；y'——响应面法响应变量；yi——i组分中气相的摩尔分数，%；zi——i组分中液相的摩尔分数，%；αl——l相在纵向和两个横向的扩散系数，m；γT——热膨胀系数，K-1；γTd——膨胀过程的热膨胀系数，K-1；γTi——i组分的热膨胀系数，K-1；γTppac——压实过程的热膨胀系数，K-1；γTpor——孔隙体积热膨胀系数，K-1；µl——l相的黏度，Pa·s；μo——重油、轻质油及溶解气混合物的黏度，Pa·s；μoi——i组分的黏度，Pa·s；ρl——l相的密度，kg/m3；ρs——基质密度，kg/m3；τ——基质的迂曲度，无因次；φ——孔隙度，%；φmax——最大孔隙度，%；φref——参考压力下的孔隙度，%；φref,f，φref,s——参考压力下流体、固相占据的孔隙度，%。下标：ref——参考值。