多因素约束下公路桥涵装配式构件生产车间工期优化模型及应用*

李佳希 于竞宇 陈川辉 王波

(合肥工业大学土木与水利工程学院，安徽 合肥 230009)

0 引言

2020年，住房和城乡建设部、国家发展和改革委员会等部委联合印发《关于推动智能建造与建筑工业化协同发展的指导意见》(建市〔2020〕60号)，提出推动建筑工业化、数字化和智能化升级，助推建筑业高质量发展。2021年，中共中央、国务院印发《国家综合立体交通网规划纲要》，提出到2035年，国家综合立体交通网实体线网总规模合计70万km左右(不含国际陆路通道境外段、空中及海上航路、邮路里程)。在加快建设交通强国、构建现代化高质量综合立体交通网的背景下，公路桥涵建设面临新的要求。

在国家相关政策推动下，装配式建筑得到快速发展。与传统公路桥涵构件生产模式相比，公路桥涵装配式构件所有生产工序均在室内车间进行，可确保预制构件各道工序全天候、不间断生产，不受大风、降雨、冰冻等不利自然气候条件影响，有效提高了公路桥涵装配式构件产能。同时，公路桥涵装配式构件预制生产质量更加可控[1]。公路桥梁大型装配式构件生产属于典型的混合流水车间调度问题(Hybrid Flow Shop Scheduling Problem，HFSP)，可以描述为：在生产流水线上对N个独立的构件进行生产，该生产系统中的每一个构件都有I道工序，每一道工序都有J台设备，且每一个需要生产的构件中至少有一道工序需要多台并行机，设备使用情况符合占用约束和顺序约束。

公路桥涵装配式构件体积大、生产车间内部空间受限，同时需要满足公路项目建设施工需求，因此生产工期较紧。目前，公路桥涵装配式构件的生产过程中人工投入大、生产效率低，且车间内存在生产缺乏规划、布局不合理等问题。为了进一步优化生产工期，提高车间内的生产效率，本文提出一种多因素约束下公路桥涵装配式构件生产车间工期优化模型。

1 文献综述

近年来，随着装配式构件的快速发展，装配式构件的生产调度问题得到业界学者关注。龙春晓[2]从预制构件生产流程入手，对生产工序进行划分，并根据实际数据求出每项工序的学习曲线方程，结合生产过程的其他限制条件，建立适用于预制构件生产过程的人力配置方案；谢思聪等[3]在对比分析预制构件生产与一般制造业区别的基础上，提出预制构件厂生产参数的量化途径，采用基于多层编码遗传算法解决预制构件的生产调度优化问题；李莹莹[4]指出，目前我国装配式建筑发展仍处于探索阶段，规模化、标准化、工业化、通用化、产业化水平不高，初期投资成本较大，诸多原因导致装配式工业化建筑成本偏高；Mahdavi等[5]通过工人资源的分配优化，实现了对工人资源的多目标优化调度研究；Ko等[6]以最短完工时间和延误或提前交货惩罚成本为目标，构建多目标预制构件生产调度模型；Yang等[7]以完工时间、合同罚款、工作站空闲时间最短等为目标，构建多条预制生产线的生产调度模型；Wang等[8]考虑了模具制造、运输过程等对预制构件生产的影响，以最小化拖延和提前处罚的总成本为目标，构建了改进的预制构件生产调度模型；Ma等[9]提出了预 制 生 产 线 流 水 作 业 调 度 模 型(MP-FSM)和基于遗传算法的流水作业调度优化方法，实现了多生产线流水作业调度的优化；赵芮等[10]以最小化最大完工时间和最小化最大拖期为目标，提出了一种多目标离散正弦优化算法方法。

由此可见，对于车间调度优化问题的求解，智能优化算法是最主要的手段，也是当前生产调度领域的研究热点。目前，车间生产线调度使用较多的求解算法有遗传算法、蚁群搜索算法、模拟退火算法、粒子群算法等。遗传算法应用领域广泛，具有群体搜索的特点，适用于复杂大型的非线性问题，但容易出现过早收敛的问题，且效率不高；蚁群搜索算法全局搜索能力强但局部搜索能力较弱，往往只能得到次优解；模拟退火算法全局寻优能力强但效率不高；粒子群算法搜索速度快，但极易陷入局部最优；正余弦优化算法具有高度的灵活性，原理简单，易于实现。

在装配式构件生产和调度问题相关研究中，研究对象大多是体积/质量小、生产工序复杂的小型装配式构件，对于大型装配式构件的研究集中于构件结构设计、建造技术、质量管理等方面。王彬等[11]提出了装配式构件的新工法；史宏刚等[12]结合实际问题，为提升构件生产质量提供技术保障。基于此，本文考虑多种约束因素，如受季节因素影响的生产时长和受工作时间约束的工人影响，利用正余弦算法建立一种适用于公路桥涵大型装配式构件的生产车间工期优化模型，并在实例中进行验证，通过借助收敛速度较快且具有高探索性和局部最优避免性的正余弦算法求解，达到工期最优化的目的。

2 公路桥涵装配式构件生产车间工期优化模型构建

2.1 模型描述

作为典型的HFSP问题，公路桥涵装配式构件生产车间优化可描述为：数量为N的构件需要在I段工序J条生产线上完成生产，每段工序上有J个生产工位，每个构件的生产顺序相同。调度目标为：N个构件生产的最短工期。

与传统问题不同的是，公路桥涵装配式构件体积大、影响因素多，具有一定的特殊性，因此，生产时需要考虑多种因素。本文考虑受工作时间约束的工人和受季节因素影响生产时长的工段，以此为每个构件的每段工序确定最佳生产工位，进而提高确定N个构件生产最短工期的准确性。模型符号和变量定义见表1。

表1 模型符号和变量定义表

同时，根据生产要求做出以下假设：

(1)在所有工序开始前，工人和机器准备就绪，不考虑准备工作时间。

(2)不考虑构件加工过程中工序之间的运输转移时间。

(3)不考虑机械故障。

(4)不考虑生产过程中出现质量问题导致的重新加工。

(5)车间内构件的生产工序一开始已确定。

2.2 模型构建

分析受工作时间约束的工人和受季节因素影响生产时长的工段，建立以生产工期为优化目标的车间调度优化模型，即

Obj.MIN(TN)=MIN(max(tfijn)1≤j≤J，1≤i≤I-
min(tsij11)1≤j≤J，1≤i≤I)

(1)

s.t.

max(Y，Z)≥6l，min(Y，Z)≥4+2bJ

(2)

ts(i+1)n>tfin

(3)

tijk=w×tij

(4)

Ht≤Hmax，Hmax=(max(Y，Z)-6l)×J/l

(5)

式(1)表示目标函数生产工期最小化；MIN表示最小值函数；min表示最早时间值；max表示最晚时间值；max(tfijn)1≤j≤J，1≤i≤I表示最后一个进行第I个工序的公路桥涵装配式构件完成第I个工序加工的自然时间；min(tsij11)1≤j≤J，1≤i≤I表示最早一个进行第一个工序的公路桥涵装配式构件开始第一个工序加工的自然时间。

式(2)表示车间场地面积约束，根据车间场地面积和待生产装配式构件的长度宽度确定生产线J的总条数；式(3)表示工序时间约束，其中，ts(i+1)n表示第n个待生产装配式构件在任一生产线上开始加工第i+1个工序的自然时间，tfin表示第n个待生产装配式构件在任一生产线上完成加工第i个工序的自然时间；式(4)表示受季节因素影响的生产时长，其中，tij表示第j条生产线第i段工序的基准时间，基准时间为工序在设定的生产环境下加工时间，tijk表示当前生产环境下第j条生产线第i段工序上加工第k个T梁的预测时间，w表示生产环境对基准时间的影响系数，w为经验值，一般春秋季取值为1，夏季取值为0.7～0.9，冬季取值为1.1～1.3；式(5)表示堆积约束，即生产过程中可在装配式构件生产车间内短暂堆积未加工完成的构件约束，其中，Ht表示t时刻装配式构件生产车间内短暂堆积未加工完成的构件数量，Hmax表示T梁车间内允许最大堆积的未加工完成构件数量。

3 正余弦算法

3.1 算法简介

正余弦优化算法(Sine Cosine Algorithm，SCA)是一种新型智能优化算法。在算法中会生成多个初始随机候选解，并使它们基于正弦和余弦的数学模型向外波动或向最优解的方向波动，利用多个随机变量和自适应变量来计算当前解所在位置，从而可以搜索空间中的不同区域，有效地避免局部最优，收敛于全局最优。

正余弦优化算法具有高度的灵活性，原理简单，易于实现，适用于不同领域的优化问题。正余弦优化算法的寻优过程可分为两个阶段：在探索阶段，优化算法通过结合某随机解在所有随机解中快速寻找搜索空间中的可行区域；在开发阶段，随机解会逐渐发生变化，且随机解的变化速度会低于探索阶段的速度。在正弦余弦算法中，候选解会被随机初始化，再根据正弦或者余弦函数并结合随机因子来更新当前解在每一维度上的值。

3.2 编码方案与初始化

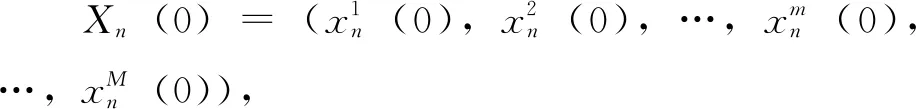
3.3 参数设置

第t+1次迭代时个体第m维位置分量的更新为

r1=a×(1-t/tmax)

(7)

在式(7)中，tmax为最大迭代次数；a为常数，一般取值为2。

3.4 算法求解流程

使用正余弦算法求解多因素约束下公路桥涵装配式构件生产车间最短工期，算法流程图如图1所示。

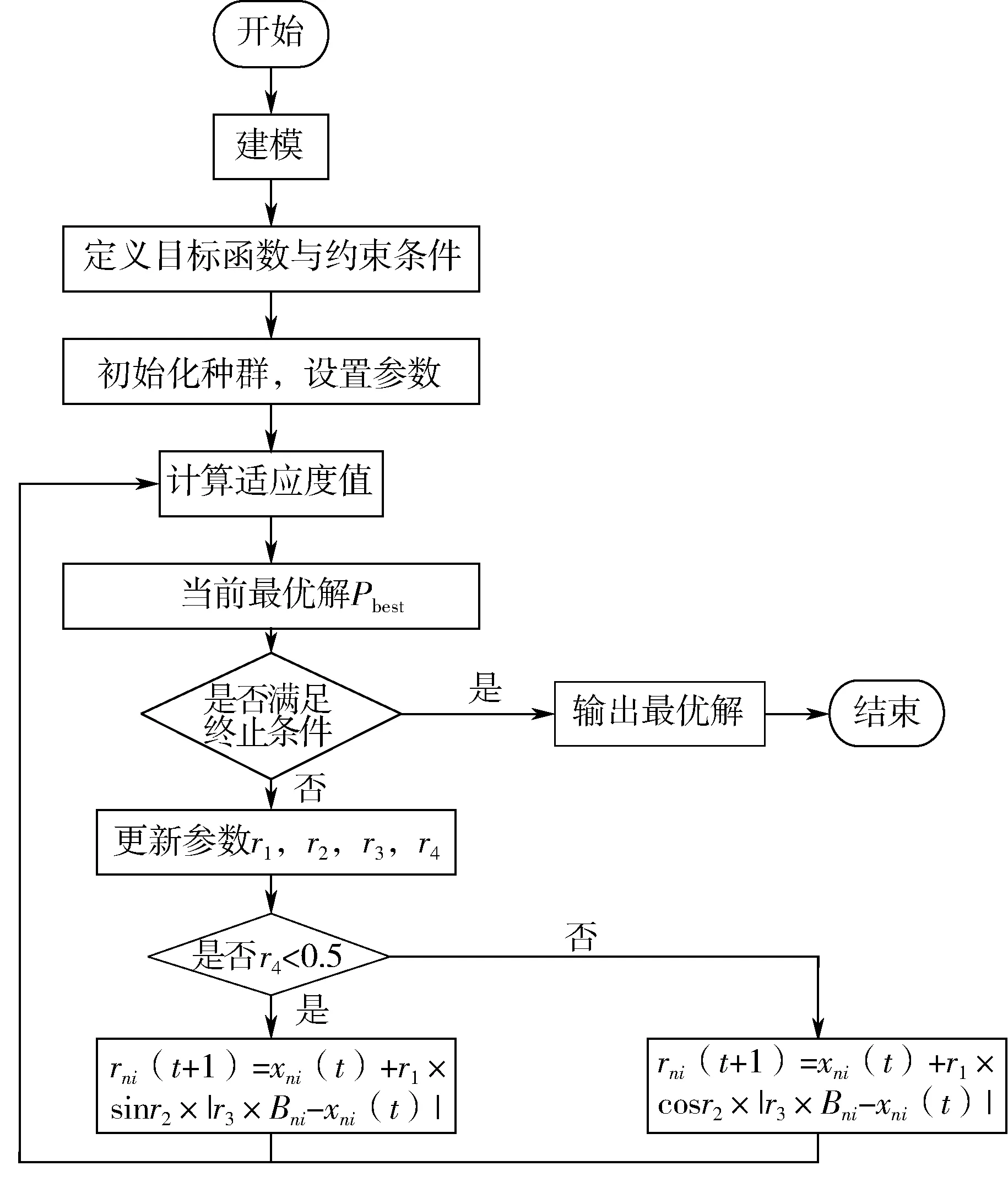
图1 正余弦算法求解最短工期流程图

具体步骤如下：

(1)建立构件生产车间受多因素约束的数学优化模型，将最短工期定义为优化模型的目标函数，确定决策变量和约束条件。

(2)定义求解构件生产车间最短工期中采用基于工件排序的自然数编码。

(3)种群初始化。初始种群随机产生，随机的初始种群更有可能在迭代之初遍布可行域的搜索空间，提高算法的多样性。

(4)设置r1、r2、r3、r44个参数，r1由式(7)决定，r2是[0，2π]之间的随机数，r3是[0，1]之间的随机数，r4也是[0，1]之间的随机数。

(5)根据式(6)计算当前适应度值和当前最优解Pbest。若不满足终止条件，则执行步骤4，进入迭代循环。反之，输出最优解，结束迭代。

4 案例分析

4.1 案例简介

本文以D梁厂为例进行分析。D梁厂施工区域分为轻型T梁预制区、箱涵拱涵预制区、圆管涵盖梁预制区、钢筋加工场，预制总砼方量为14.25万m3。T梁车间面积为124m×54m；车间内工人工作时间为8：00～12：00，14：00～18：00，单休。该车间主要生产的公路桥梁大型装配式构件为25m轻型T梁，台座尺寸为100cm×1504cm×2490cm。原计划采用固定模台生产线布局形式，生产线采用移动台座+固定液压模板的形式，模板采用底模移动，侧模固定方式，每条生产线配备1套液压模板，4个移动台座，生产线分为钢筋绑扎工位、混凝土浇筑工位、蒸养工位、张拉压浆工位。工序如下：

(1)钢筋绑扎。可间断，必须在工作时间段开始，也必须在工作时间段完成。一片T梁在该工序生产时间t1=24/人数(h)。

(2)混凝土浇筑。不可间断，必须在工作时间段开始并在同一工作时间段完成。一片T梁在该工序生产时间t2=1.5h。

(3)脱模。混凝土浇筑结束立即开始计算脱模时间，可在任意时间段完成。现取一片T梁在该工序生产时间t3=10w3。w3为季节系数，春秋w=1；夏季w=0.8；冬季w=1.2。

(4)蒸养。必须在工作时间段开始，可在任意时间段完成。现取一片T梁在该工序生产时间t4=24w4。w4为季节系数，春秋w=1；夏季w=0.9；冬季w=1.1。

(5)张拉压浆。不可间断，必须在工作时间段开始并在同一工作时间段完成。一片T梁在该工序生产时间t5=1h。

4.2 仿真分析

正余弦算法的参数设置如下：种群规模为1920，最大迭代次数为100。正余弦算法收敛曲线如图2所示，调度甘特图如图3所示。

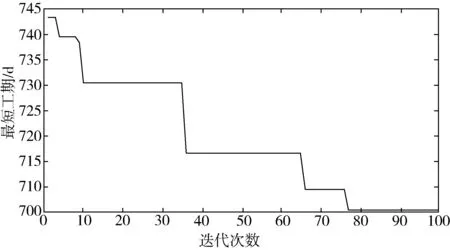
图2 正余弦算法收敛曲线

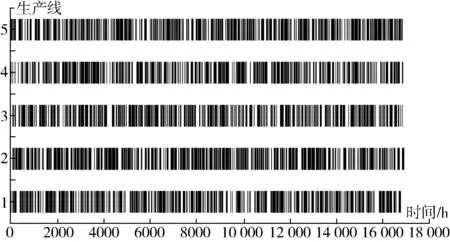
图3 调度甘特图

4.3 结果分析

通过优化前后的对比结果(表2)可知，工期缩短38d，人工量减少760工日。本次优化严格按照工人工作日历安排生产工作，考虑工序受各生产因素影响，尽可能地优化了最短工期，有效减少了人工成本。通过对此次优化进行详细分析可知，工期优化主要集中在钢筋绑扎和混凝土浇筑两个工序。通过合理安排工人数量对各工序做出最优调度安排。

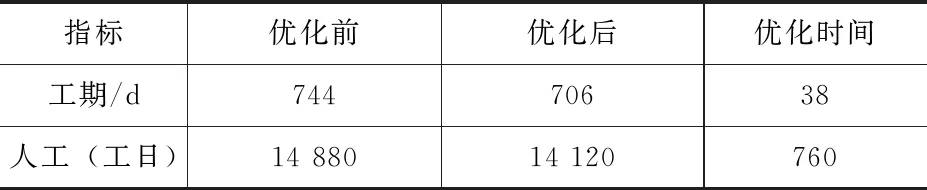
表2 优化前后对比结果

5 结语

本文在考虑公路桥涵装配式构件生产时间受工人的工作日历影响和生产工序时长受季节因素影响的基础上，构建针对公路桥涵装配式构件生产车间工期优化模型，并使用实际算例进行验证。通过该模型使用正余弦算法求出算例中车间内生产任务的最短工期，并对车间内各待生产构件的工序做出最优调度安排。实验结果表明，该方法优化了最短工期，有效减少了人力和生产成本。同时，正余弦算法收敛速度快，适用于装配式构件生产研究，可为其他类似预制构件生产的调度安排提供参考。