基于障碍Lyapunov函数的未知控制方向非线性系统的约束鲁棒输出调节

孙伟杰,乔雨晨,彭云建

(华南理工大学自动化科学与工程学院,广东广州 510640)

1 引言

输出调节问题旨在为不确定系统设计反馈控制器,使得受控闭环系统在内部状态有界的前提下,其输出可以在抵抗干扰的同时而渐近跟踪上给定的参考信号.这类问题也可以称为渐近跟踪或抗干扰问题,在控制领域得到了广泛关注[1–5].

然而,实际物理系统受到外界环境或自身物理结构的约束.因而,在对非线性系统进行反馈控制规律的设计时,必须考虑受控系统的暂态性能.例如,在人机交互设计中,需要对机器人机械手的位置进行约束,以避免与人或周围环境的碰撞[6–8].此外,不确定系统存在控制方向未知的问题,对控制系统的设计带来了挑战[9].20世纪80年代提出的Nussbaum增益技术是处理未知控制方向的标准方法[10].

在考虑非线性系统的约束输出问题时,障碍Lyapunov函数(barrier Lyapunov function,BLF)技术得到了广泛应用[11–13].与二次型Lyapunov函数(quadratic Lyapunov function,QLF)不同,BLF不是径向无界的,而是在其参数接近某一有限值时趋近于无穷大[11–12].这一特性使得BLF技术可应用于系统输出受到约束的非线性系统控制问题.为了放松静态约束的要求[11],并降低设计保守性,文献[13]进一步发展了时变BLF技术,允许期望输出被限制在给定的时变范围内.

基于BLF的控制技术已被成功应用于解决具有输出约束的各类非线性系统[14–15].然而,现有的研究大多基于逆跟踪设计方法,这种方法普遍需要依赖于跟踪参考信号的高阶差分信息[16].在实际应用中,对信号的高阶微分会引入噪声放大问题.最近,文献[17–19]结合Nussbaum增益技术,将BLF技术应用到控制方向未知的非线性系统跟踪控制问题中,采用模糊控制和神经网络设计框架,使跟踪误差收敛到零附近的一个紧集中.与基于逆跟踪的方法相比,输出调节设计框架基于内模原理[20],消除对高阶微分信息的依赖要求,而且能够保证跟踪误差渐进收敛到零.

文献[3–4]利用Nussbaum增益技术研究了非线性输出反馈系统控制方向未知时的输出调节问题.文献[5,21]考虑了外部系统含有未知参数的情况.以上研究成果都未考虑被控系统的输出约束.基于文献[13]的BLF技术,文献[22]研究了一类非线性系统的约束输出调节问题,但其要求系统的控制输入方向已知.因此,文章将结合BLF方法和Nussbaum增益技术,讨论一类非线性系统控制方向未知时的约束鲁棒输出调节问题,使得系统的跟踪误差能渐近趋近于零,而且一直保持在给定的限制区域内.

本文基于解决鲁棒输出调节问题的一般框架[20]:首先,将非线性系统的约束鲁棒输出调节问题转化为增广系统的约束鲁棒稳定问题;然后,将BLF方法与Nussbaum增益技术相结合,解决增广系统的约束鲁棒稳定问题;最后,选用Lorenz系统进行数值仿真,验证反馈控制器的合理性,并与基于QLF设计的仿真结果进行对比,表明反馈控制器的有效性.

2 问题描述及预备知识

考虑如下的一类非线性系统:

其中:z ∈Rn,y ∈R和e ∈R分别表示非线性系统的状态、输出和输出跟踪误差,u ∈R代表系统的控制输入,w∈W ⊂Rnw表示系统中的不确定参数,v∈V ⊂Rnv表示外部系统信号.给定的目标输出参考信号yr∈R由如下的线性外部系统提供:

系统(1)中的所有函数都是充分光滑的.同时,系统的控制输入增益b(w)≠0,但符号未知.对于已知的σ ∈S ⊂Rl,系统(2)中矩阵A(σ)的所有特征值互异,并且实部都为零.因此,外部系统(2)能够产生有限个阶跃函数和正弦函数的组合,其幅值和相位由外部系统的初始条件决定.

本文研究的问题描述如下: 对系统(1)建立如下形式的动态输出反馈控制律:

使得非线性系统(1)和控制器(3)组成的闭环系统状态有界,跟踪误差e渐近趋于零,并且输出y(t)满足|y(t)|≤kc(t),∀t≥0,其中:(M,N)是一对待定矩阵,F(·),ρ(·)是η,k,e的待设计函数,kc(t)是一个与时间有关的给定约束.

注1在控制器(3)中:η表示内模状态[2],u为系统(1)的控制输入,k为高增益参数.由于考虑的外部系统(2)是线性的,因此内模η的动态行为是线性的.

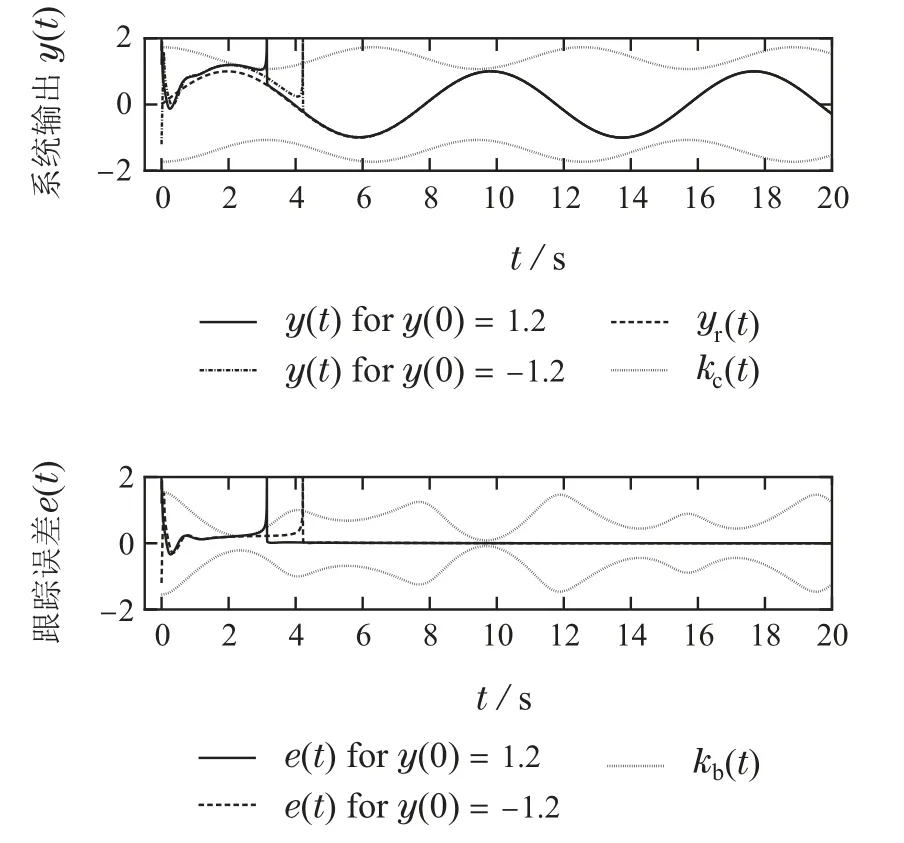
如果t≥0,w∈W ⊂Rnw,v(t)∈V ⊂Rnv,那么存在一个与期望输出yr(t)有关的函数r(t),并且满足r(t)≥|yr(t)|.定义函数kb(t)=kc(t)-r(t).如果∀t≥0,|e(t)|

通过上述变换,可以将系统的输出约束转化为系统的输出跟踪误差约束,其中kb(t)是跟踪误差的约束函数.通过引入r(t),将被控系统的输出约束问题转化为跟踪误差约束问题.根据文献[20]中提出的输出调节设计框架,引进如下标准假设:

假设1存在一个满足z(0,w,σ)=0的充分光滑函数z(v,w,σ):Rnv×Rnw×Rl →Rn,且

根据假设1,令y(v,w)=q(v,w),可以计算得到

此时,z(v,w,σ),y(v,w,σ)和u(v,w,σ)给出了系统(1)的调节器方程的解[2].为了构造线性动态补偿器来重建稳态控制输入u(v,w,σ),引入如下假设:

假设2函数u(v,w,σ)是有关v的多项式,并且该多项式的系数依赖于不确定性参数w和σ.

注2由文献[2]和文献[23]可知,对于线性外部系统(2),如果系统(1)中的函数f(z,y,v,w)是(z,y,v)的多项式,且系数依赖于w,则假设1中的z(v,w,σ)一定有解.此时,如果系统(1)中的函数g(z,y,v,w)和q(v,w)也是关于(z,y,v)的多项式且系数依赖于w,则假设2得到满足.

由文献[21]可知,存在一个正整数s,对于外部系统(2)的v以及任意的(w,σ)∈W×S,函数u(v,w,σ)满足下面方程:

其中h1(σ),h2(σ),···,hs(σ)为实数,并且对于任意的σ ∈S,多项式

具有实部为零的各个互异根.

定义π(v,w,σ)=[u···u(s-1)]T,则有

其中:ϑ(v,w,σ)=T(σ)π(v,w,σ),Ψσ=ΨT-1(σ).

根据式(6),构造如下动态补偿器:

上式可称为系统(1)输出为u的内模[20].

将内模动态方程(7)与非线性系统(1)合并,然后进行如下的坐标变换:

可得增广系统

其中:b=b(w),=u-Ψση.因此,如果存在控制器

可以解决增广系统(9)在跟踪误差受约束且控制方向末知情况下的稳定性问题,则控制器

可以解决系统(1)的约束输出调节问题[20].

3 主要结果

这一部分,本文将使用BLF技术和Nussbaum增益技术解决增广系统(9)的约束镇定问题.为此,引入如下引理1[11]和假设3[21].

引理1对正常数k1和k2,令开区间Z={ξ ∈R:-k1<ξ

其中:ζ=(ω,ξ)T∈N,函数h:R+×N→Rl+1在时间t上分段连续且对ζ满足局部Lipschitz条件.假定存在两个正定可微的函数V1:Z →R+和U:Rl×R+→R+,并分别满足如下条件:1)V1(ξ)→∞,当ξ →-k1或ξ →k2时;2)γ1(‖ω‖) ≤U(ω,t) ≤γ2(‖ω‖),其中: 函数γ1(·)和γ2(·)均为K∞类函数.令函数V(ζ)=V1(ξ)+U(ω,t)且初始值ξ(0)∈Z.对于ξ ∈Z,如果,则对t≥0的时刻,有ξ(t)∈Z.

假设3考虑增广系统(9),对于所有的µ=(v,w)∈Σ ⊂Rnv×Rnw,存在一个满足下面条件的C1函数V():

其中:δe是未知正常数,γe(·)是已知光滑正函数.

选择改进型障碍Lyapunov 函数(modified barrier Lyapunov function,MBLF)

其中:ln(·)表示自然对数,exp(·)表示以自然常数e为底的指数函数.式(14)的MBLF函数,既适用于处理有输出约束的情况,又可以处理无输出约束的情况,扩展了BLF技术的应用范围[16].同时,由于非系统(1)的控制输入方向未知,本文选择Nussbaum增益函数[3]为N(k)=k2cosk.

引理2在假设3下,对于增广系统(9),考虑如下形式的控制器:

则存在正常数p,光滑实函数ρ(·)≥1和Lyapunov函数V,并且V沿着闭环系统轨迹的导数满足

证首先,将增广系统(9)的子系统动态(,)看作文献[21]中方程(17)的形式,其中

因此,在假设3下,依据文献[21]中的引理3.1可得,对任意的µ ∈Σ,存在一个满足下面条件的C1函数V1(,),即

其次,对式(14)中的MBLF函数VMBLF求导,可得

其中:Z=col(,),p1是未知正常数,∆1(Z)和ρ1(e)是两个光滑的正实函数.

定义Lyapunov函数V=U(Z)+VMBLF.结合式(21)–(22),可得V沿着增广系统(9)和控制器(15)组成的闭环系统的轨迹满足

根据引理2,可得到如下定理.

定理1在假设1–3下,如下反馈控制器:

可以解决非线性系统(1)在控制方向末知情况下的约束鲁棒输出调节问题.

证在时间区间[0,t),∀t≥0上,对不等式(16)的两边同时积分,可得

根据式(26)以及文献[25]中的引理1,对于时间区间[0,T),0

4 数值仿真

考虑以下Lorenz系统[3]:

其中:(L1,L2,L3)是系统的常参数向量,L1>0,L2<0,并且b是一个未知符号的非零常数.

系统输出y(t)要实现跟踪的正弦参考信号v1(t)由外部系统(2)产生,初始状态v0=[0 1]T.同时,要求系统输出y(t)满足|y(t)|≤kc(t),∀t≥0,其中kc(t)=1.4+0.33 cost.选取参考信号上限函数(t)中的参数λ=0.5,可得跟踪误差约束函数kb(t)=kc(t)-(t).

由文献[3]可知,假设1–2得到满足,并且

选择能控矩阵对

根据第3 部分给出的设计思路,可得ρ(e)=11.选取正弦参考信号的频率σ=0.8,给定Lorenz系统的参数L1=10,L2=-,L3=28,系统的初始状态为(z1(0),z2(0))=(2,-1),η(0)=0和k(0)=1.

系统输出y(t)的初始状态分别设置为y(0)=1.2和y(0)=-1.2,分析可得|e(0)|

图1 b=1时,输出y(t)的响应曲线(MBLF and BLF)Fig.1 Profile of y(t),when b=1 with MBLF and BLF

图2 b=1时,输出e(t)的响应曲线(MBLF and BLF)Fig.2 Profile of e(t),when b=1 with MBLF and BLF

图3 b=-1时,输出y(t)的响应曲线(MBLF and BLF)Fig.3 Profile of y(t),when b=-1 with MBLF and BLF

图4 b=-1时,输出e(t)的响应曲线(MBLF and BLF)Fig.4 Profile of e(t),when b=-1 with MBLF and BLF

图5 b=1时,y(t)和e(t)的响应曲线(QLF)Fig.5 Profile of y(t)and e(t),when b=1 with QLF

图6 b=-1时,y(t)和e(t)的响应曲线(QLF)Fig.6 Profile of y(t)and e(t),when b=-1 with QLF

5 总结

本文讨论了一类非线性系统在控制方向未知下的约束鲁棒输出调节问题.在基于内模原理的输出调节框架下,文章综合利用障碍Lyapunov函数与Nussbaum增益函数相结合的技术方案,设计对应的输出反馈控制器.以Lorenz系统为仿真实例,与基于传统二次型Lyapunov函数设计的仿真结果对比,表明了本文控制方案的有效性.未来工作可考虑将研究方法推广至其他类型非线性系统的类似输出约束问题.