基于混合阈值事件触发机制的船舶自适应神经滑模控制

李纪强 ,张国庆,张显库 ,张卫东

(1.大连海事大学航海学院,辽宁大连 116026;2.上海交通大学电子信息与电气工程学院,上海 200240)

1 引言

船舶航向保持控制是船舶在航行过程中的一个最基本的任务场景.针对船舶航向保持控制研究,已经取得了大量的有益成果,例如比例积分微分(proportion integration differentiation,PID)控制、自适应神经控制、模型预测控制、滑模控制、动态面控制等[1–5].文献[6]对船舶航向保持控制的发展历程进行了系统的研究,并且指出,PID控制由于参数少和控制器结构简单的优势,被广泛应用到航向自动舵中.但是PID控制律是基于精确数学模型设计的,而船舶的运动特性易受模型不确定、风浪流干扰等因素影响,因此用于控制算法设计的数学模型与实际物理平台之间存在很大的不确定性.为了处理模型结构的非线性项,文献[7]中采用径向基函数神经网络(radial basis function neural networks,RBF-NNs)对模型不确定进行在线逼近,并且利用Lyapunov稳定性判据证明了闭环控制系统的稳定性.进一步,文献[8]提出了一种双极性S函数修饰的非线性控制律,所提控制算法能够在保持控制效果的同时降低控制能量,并且以“育鲲”轮为例进行了仿真验证.文献[9]中分别针对船舶Nomoto模型设计非线性修饰的控制算法与模糊控制律,并进行仿真效果对比,结果表明两种控制算法均具有良好的鲁棒性和控制效果,但是使用非线性修饰的航向保持控制算法能够减少平均舵角的使用次数.在外界海洋环境作用下,船舶为了保持在期望航向,控制系统需要不断更新命令信号来调整舵角,这会造成执行器的频繁操纵,增加舵机能量消耗.在文献[10]中,基于牛顿–拉格朗日非线性数学模型,设计了一种具有扰动观测补偿机制的航向保持控制律,通过仿真验证说明了所提扰动观测器能够降低时变干扰对控制系统的影响.文献[11]提出了一种基于比例积分滑模的自适应控制律,通过对航向误差和位置误差的镇定来实现欠驱动船舶的路径跟踪任务.

实际上,上述文献中是基于连续时间采样设计的航向保持控制律,这会在一定程度上造成控制命令对传输信道的资源占用,并且增加舵机损耗.事件触发技术作为一种能够降低通信复杂的有效控制算法,已经在多智能体系统和船舶路径跟踪控制中得到了广泛的应用[12–14].文献[15]介绍了一种能够保证非线性系统的控制器和参数估计器同时触发的触发条件,并且避免了输出到状态稳定的假设前提.文献[16]针对无人船编队控制问题,利用鲁棒神经阻尼技术提出了一种了鲁棒自适应事件触发控制算法,证明了事件触发技术在降低通信负载方面的优势性.在文献[17]中,进一步将事件触发控制算法引入到无人帆船的航向保持控制中,设计了一种考虑执行器故障的事件触发控制算法,并且在仿真部分验证了事件触发技术在降低系统振动方面的优势.在文献[12–17]中,事件触发阈值参数需要人为设定,即控制系统是静态触发的.对于船舶艏向自动控制来说,在瞬态响应阶段和稳态响应阶段,对于阈值参数的需求是不一致的.为了解决这种问题,文献[18]针对非线性系统设计了一种自适应律来动态调节阈值参数.这种方法在瞬态响应时会有效降低触发次数,但是阈值参数会随着时间增加而逐渐趋近于零.尽管事件触发技术能够有效减少控制命令的传输次数,但是一个不可避免的问题是,在触发间隔内控制命令保持不变,会降低系统的控制输出精度.

基于以上分析,本文以牛顿–拉格朗日非线性数学模型中艏向模型为控制对象,在时变干扰环境下设计了一种基于混合阈值事件触发机制的船舶自适应神经滑模控制算法.在所提控制算法中,利用径向基神经网络逼近艏向模型中的非线性项,并且通过两个自适应更新参数对神经网络权重和执行器增益进行在线补偿.本文的创新点主要总结为以下两点:

1)与文献[10]相比,基于混合阈值参数的事件触发机制能够在瞬态响应阶段动态调节阈值参数,在稳态响应阶段实现静态触发.这会降低闭环系统在瞬态响应阶段的触发次数,减少舵机能量消耗;

2)引入比例积分滑模技术,降低了事件触发技术在减少控制命令传输负载时引起的控制输出抖振.此外,从理论上证明了事件触发技术对外部干扰的鲁棒性.

2 模型描述

欠驱动船舶的牛顿–拉格朗日非线性数学模型的矩阵表达如下:

式中:η=[x y ψ]T为船舶的位置和艏向信号;v=[u v r]T表示船舶前进速度、横漂速度和艏摇角速度;d为外部扰动矩阵;τ=[τu0τr]T表示船舶的推进力和转船力矩;J(η)表示转换矩阵,详细的模型介绍可以参阅文献[19].

为便于艏向保持控制器设计,将式(1)中的艏向模型写为

其中:fr(v)表示艏向模型中的非线性项,Fr(·)表示执行器增益函数,δr表示舵角,c1,c2表示科式向心系数,d1,d2表示水动力阻尼系数,gr表示未建模动态.dwr表示外部扰动,mr表示艏向方向上的附加质量.

在船舶艏向模型的非线性项(3)中,包含前进速度u和横漂速度v,即r与u,v存在一定耦合作用,因此,在欠驱动船舶模型的基础上研究船舶艏向运动更加符合工程实际.

为了增加控制器设计的严谨性,有以下假设.

假设1对于外界海洋环境随机扰动dwr存在未知常量>0,满足|dwr|≤.

假设2船舶横向漂移速度小于前进速度,即横向漂移速度被动有界稳定[10].

3 自适应神经滑模控制器设计

3.1 控制器设计及稳定性分析

步骤1定义误差变量ψe=ψd-ψ,并对其求导得

式中ψd表示期望航向,且二阶可导.为了镇定艏向误差ψe,构造Lyapunov候选函数如下:

对V1求导得

针对r设计虚拟控制律αr如下:

式中k1>0为设计参数.因此,可以重新写为

其中re=αr-r.

步骤2对误差re求导得

为了镇定误差re,构造比例积分滑模修正面ξ1,即

式中k2为大于零的滑模面设计参数.进一步可以得到

构造Lyapunov函数V2如下:

对V2求导,可得

由于在式(14)中出现了ξ1,因此构造V3,即

对V3求导,并将式(11)代入,可得

对于式(16)中的非线性项fr(v),采用径向基函数神经网络进行在线逼近,如下:

式中:W表示更新权重,S(v)表示高斯函数,ε(v)为具有误差上界(v)逼近误差.

为了避免连续生成控制命令,增加对信道资源的占用,引入事件触发机制.考虑事件触发机制的控制输入如下:

事件触发条件为式(19),即控制输入在不满足触发条件时,控制输入保持不变,当满足触发条件时,控制输入更新.

式中:eδ=δk-δr,ω1,ω0分别表示动态/静态触发阈值参数,δ∆>0为正的常数.根据式(19),有以下两种情况.

情况1如果δr≥0,可以得到-ωδr-δ∆≤δk(t)-δr(t)≤ωδr+δ∆,进一步可以表述为

情况2如果δr<0,可以得到ωδr-δ∆≤δk(t)-δr(t)≤-ωδr+δ∆,进一步可以表述为

根据情况1和情况2,可以得到

将式(17)和式(23)代入式(16)中,可以得到

选取αδ作为中间控制变量,定义变量ϱ=mr(1+λ1ω)/Fr,为ϱ的估计值,且有=ϱ-.因此,设计鲁棒自适应神经滑模控制律如下:

将式(26)代入式(25)中,可以得到

式中γ1,γ2,σ1,σ2表示正的自适应设计参数.

定理1若船舶艏向系统(2)满足,其中∆0为正常数,在满足假设1和假设2的前提下,综合应用虚拟控制律(7)、事件触发机制(18)、控制律(26)和自适应律(28),可以得到以下两点:

1)船舶艏向系统内所有状态变量满足半全局一致最终有界(semiglobal uniform and ultimately bounded,SGUUB)稳定;

2)通过调节设计参数可使得艏向误差收敛到零点的任意小邻域内.

为证明定理1,构造Lyapunov函数V4,即

对V4求导得

将式(28)代入式(30)可得

利用以下不等式对式(31)进行放缩设计:

因此,式(31)可以被写为

进一步可以得到

3.2 事件触发技术的鲁棒性分析

由式(19)可知,当控制输入变化满足条件(36)时,控制输入保持不变,也就是说,对于任意触发时刻的控制输入δk(tk),总会存在区间D∈[(1-ω)δk(tk)+δ∆,(1+ω)δk(tk)+δ∆]使得δr(t)=δk(tk).因此,所设计的控制律能够自动避免干扰造成的区间D内控制输入抖振.假设干扰作用在闭环控制系统上的力矩为M,M具有随机不确定性,则当满足|M|<ω|δk(tk)|+δ∆时,M对控制输入不会造成影响.

由于事件触发技术对干扰存在一定的鲁棒性,其能力强弱主要取决于触发阈值参数和触发时刻的控制输入值.对于船舶自动系统,在瞬态响应阶段为了加快追踪到期望航向,通常舵角会不断增大甚至达到饱和状态,事件触发技术会造成区间D随着控制输入的增大而增大,降低控制算法的收敛速度和控制精度.此外,触发阈值参数在控制输入较大时对控制系统的影响较大,在控制输入较小时,对控制系统的性能影响较小.航海实际中,驾驶员更希望在船舶达到稳定航行状态时能够减少由于外部干扰引起的操舵频率.

4 仿真分析

为了验证所提控制算法的有效性,将考虑前进、横漂和艏摇运动的无人船(质量为23.8 kg,船长为1.255 m,船宽为0.29 m)的3自由度耦合数学模型作为被控对象,将本文所提控制算法与算法A和算法B在MATLAB仿真平台上进行数值仿真实验,其中,算法A为文献[11]中的鲁棒自适应神经滑模控制算法.算法B为文献[18]中的鲁棒自适神经控制算法.图1为本文算法的执行流程图.

图1 MATLAB算法执行流程图Fig.1 Block diagram for MATLAB algorithm execution

船舶的非线性参数为:c1=33.8v+1.0115r,c2=-25.8u,d1=0.0313+3.96|v|+0.13|r|,d2=1.9-0.08|v|+0.75|r|,gr=0.0156ur2+0.0278uv3r,前进和横漂自由度的非线性参数可参见文献[19].控制器的设计参数为:k1=0.8,k2=2.2,ω0=0.4,δ∆=0.01,γ1=γ2=σ1=σ2=0.9.

为了构建更加符合实际的海洋环境,本文以挪威石油工业组织规范(norsk sokkels konkurranseposisjon,NORSOK)构建风干扰模型和联合北海波浪计划(joint north sea wave project,JONSWAP)构建风浪干扰模型[17].时变风场和3维风生浪如图2所示,其中,风干扰可以分为平均风分量和干扰风分量.

图2 外部干扰Fig.2 The external disturbance

设置初始航向为10◦,目标航向为80◦,仿真时间为100 s,在模拟海洋环境下进行本文算法、算法A和算法B的对比实验,仿真结果主要如图3–8所示.

图3 控制输出对比曲线Fig.3 Comparison of control output efforts

图3表示3种控制算法的控制输出曲线对比.从图3中可以看出,本文算法和算法A具有相似的输出效果,但是算法B的超调量大,控制精度低.图4表示3种控制算法的控制输入对比曲线.在航海实践中,控制命令由驾驶台计算机传出,经过舵机伺服系统传输到舵设备.图4中实线表示本文算法的控制命令δr,点线表示本文算法控制命令经过伺服系统后的实际执行舵角δ,虚线和点划线分别算法A和算法B的控制命令δr.事件触发机制能够在满足触发条件前持续保持控制命令不变,因此可以看出,本文算法的控制命令呈阶跃状,这能够降低控制器到执行器的传输频率,从而降低执行器的操舵频率.尽管算法A和算法B的控制命令曲线变化更加平滑,但是需要舵机实时操纵.通过算法A和算法B的对比,可以发现比例积分滑模技术能够提高控制输出精度和降低控制输入的抖振.图5表示非线性项fr(v)的变化曲线,以及RBF-NNs对非线性项的逼近效果.具有随机性和不确定性的外部干扰会在一定程度上降低RBF-NNs 对fr(v)的逼近效果.RBF-NNs逼近非线性项需要实时更新自适应权重参数,如图6所示.图7表示执行器增益的自适应调节参数变化曲线,当闭环控制系统达到稳态响应后,神经网络权重参数和自适应调节参数会稳定到常量的邻域内.图8表示本文所设计的自适应神经滑模控制算法的触发时间和触发间隔,从图中可以看出,最大触发间隔能够达到6.2 s,这能够极大的降低控制命令的传输频率,减少舵机操纵耗能.

图4 控制输入对比曲线Fig.4 Comparison of control input efforts

图5 非线性项和非线性项估计值Fig.5 Nonlinear term and estimate of nonlinear term

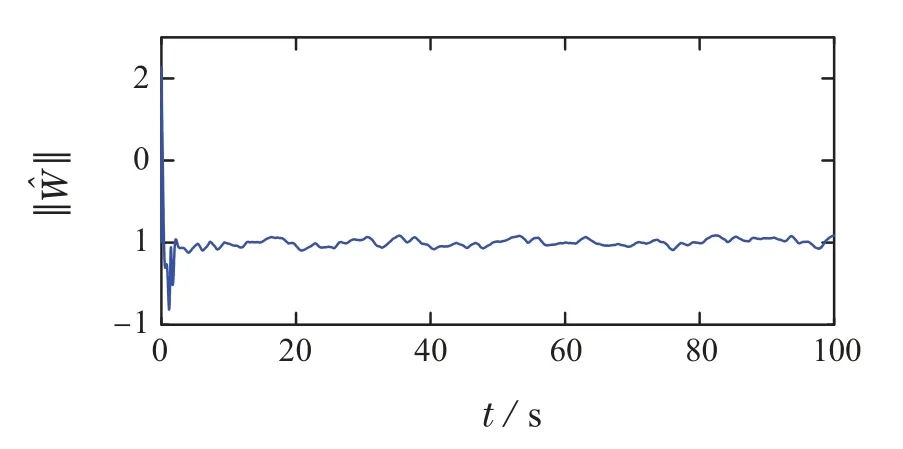
图6 神经网络的权重参数Fig.6 Weight parameter of the RBF-NNs

图8 触发时间和触发间隔Fig.8 The triggered time and triggered interval

为了进行3种控制算法的定量分析,定义3个性能衡量指标,分别是控制精度(control accuracy,CA)、输出平滑度(output smoothness,OS)和执行次数(execution number,EN).CA表示船舶航向偏离目标航向的误差平均值,OS表示船舶航向变化曲线的平滑度,EN表示闭环控制系统中控制命令的生成次数,其中CA和OS控制可由式(37)计算.主要量化结果如表1所示,从表1可以看出,本文算法精度最高,但是与算法A相比,控制输出平滑性略差,这说明事件触发技术在保证控制精度的同时,会降低控制输出的平滑性,可能的原因是在触发时刻,控制命令会发生较大的变化,控制输出响应速度快,降低输出曲线平滑性.算法A和算法B的数据对比说明了比例积分滑模技术在提高闭环控制系统的控制精度和输出曲线平滑性方面具有明显的优势.算法A和算法B的控制命令执行次数均为10000次,而本文算法的控制命令执行次数为144次.这体现了本文算法中通信信道占用少、舵机操舵频率明显下降、舵机损耗和能量消耗较低.相比之下,本文算法更具有工程实用性.

表1 控制性能定量对比Table 1 Comparison of control performances

5 结论

本文设计了一种基于混合阈值事件触发的船舶自适应神经滑模控制算法,解决了时变干扰环境下船舶航向保持控制中存在的通信受限和控制输入频繁抖振问题.所设计算法的优势主要体现在两方面: 一是控制器设计模型采用考虑前进和横漂运动的牛顿–拉格朗日非线性艏向模型,更加符合工程实际;二是控制算法中通过自适应技术构建了径向基函数神经网络更新权重和增益调节参数更新律,并且利用事件触发机制和比例积分滑模技术提高了闭环控制系统的鲁棒性和抗干扰性.最后,以具有耦合特性的三自由度船舶非线性数学模型为控制对象,在MATLAB平台上进行数值仿真,结果表明本文算法在控制精度、信道占用、舵机损耗和能量消耗方面具有明显优势.