煤矿瓦斯爆炸事故致因选取与风险等级预测

郝秦霞 ，尚海涛

（1.西安科技大学 通信与信息工程学院，陕西 西安 710054；2.西安科技大学 安全科学与工程学院，陕西 西安 710054）

煤矿的安全生产是煤矿行业健康有序发展的重要保证，以人民至上，生命至上，防范化解重大风险隐患为根本，我国提出将煤矿瓦斯风险事故防控工作的重点从事后响应向事前预防转移的号召，通过对煤矿瓦斯风险隐患预测关口前移，防范瓦斯安全事故于未然，从而遏制煤矿瓦斯事故风险。已有大量学者对瓦斯爆炸风险预控进行研究，主要包括事故风险预测与评估的研究[1]；事故致因指标与机理的研究[2]；事故致灾影响的研究[3]等。袁亮[4]通过大数据分析和数据挖掘提出煤矿动力灾害风险判识和监控预警模型；李爽等[5]通过贝叶斯网络提取多级预测指标构建煤矿风险变化趋势多级预测模型；田水承等[6]对近年来煤矿瓦斯事故调查报告进行分析，得到4 项关键致因和27 项一般致因；徐美玲等[7]从人为因素、生产设施、环境条件和管理组织多个角度分析煤矿瓦斯爆炸风险因素；鲁锦涛等[8]通过以往瓦斯爆炸案例提取影响因素，构建灰色-物元的瓦斯爆炸风险评估模型；DEY Prasanjit 等[9]构建了混合CNN-LSTM 预测模型，从矿山物联网传感器监测数据中提取空间和时间特征，有效预测不同的矿山灾害；DURSUN A E[10]对近年来土耳其煤矿发生的瓦斯爆炸事故进行了统计分析，并针对瓦斯事故提出了相应的防控措施；JUGANDA A 等[11]采用计算流体动力学（CFD）模拟长壁矿井大规模爆炸，评估瓦斯爆炸对矿井通风的影响。

1 文献分析

对于已有的瓦斯爆炸风险的研究发现，在瓦斯爆炸事故的风险预测研究中，存在以下问题：

1）以往对于瓦斯爆炸事故致因的分析多以经验分析法，如：客观权重分配法、主观层次分析法或二者结合。对实际情景、知识体系与经验分析的综合考虑不足。

2）以往对于瓦斯爆炸风险的预警大多基于时序、空间实时监测信息的预警，但瓦斯爆炸的隐患来自“人-机-环-管”等多方面彼此独立或相互影响的事故致因。

3）煤矿企业中对于风险的预警大多是基于算法模型的判断，但因地质环境、开采情况、监测条件等实际情景的差异，算法给出的预测值会出现虚警、误判，造成煤矿企业安全监管人员的懈怠思想。

综合以上问题，对于煤矿瓦斯爆炸事故致因的选取需结合煤矿实际情景、相关知识体系以及历史经验，从可能产生隐患的人员行为、监测数据等多角度考虑事故致因。对于瓦斯爆炸风险的预警，需要符合煤矿实际情景做出风险等级的分类评判，为了进行准确的风险类别预警，需采用模式分类性能较优的神经网络，以便煤矿企业安全监管人员针对风险的等级给出相应的安全防范措施。

2 基于灰色关联分析的事故致因选取

产生煤矿瓦斯爆炸的原因多样，企业采取的防控措施多以专家经验为主，但不同煤矿具有不同生产条件与特征，且在生产过程中积攒了大量具有可供参考的历史纪录。因而在分析煤矿瓦斯爆炸事故致因时，需多方面考虑并结合煤矿瓦斯安全防控的知识体系，形成多维度的事故致因。

根据以上对事故致因选择的要求，采用陕西省彬县某矿2012 年12 月至2021 年12 月间的监测数据，结合煤矿安全生产网、国家矿山安全监察局、国家矿山安全局、各省级局官方网站以及全国煤矿事故调查资料，收集近10 年来煤矿瓦斯爆炸事故案例调查报告并整理为文本集。事故致因提取的具体步骤如图1。

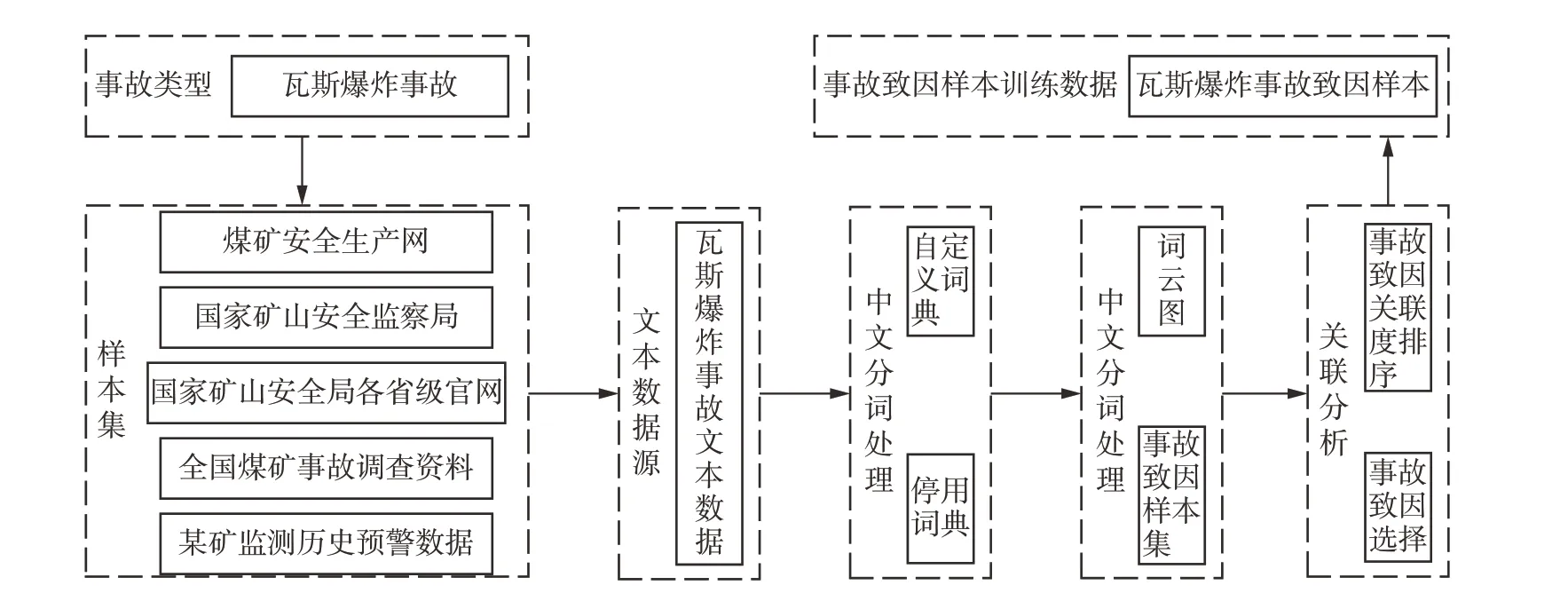
图1 煤矿瓦斯爆炸事故致因提取流程Fig.1 Extraction process of causes of coal mine gas accidents

首先对文本集数据进行清洗，将未记录事故致因的内容删除，保留事故发生时间、地点、影响结果以及原因等内容。通过R 语言Jieba 程序包对文本集进行分词处理，采用自定义词典和停用词典提高分词的准确性，提取案例报告中的事故致因。自定义词典内容主要是百度输入法词库中的煤矿术语、采矿专业领域词汇和搜狗输入法细胞词库中采矿工程、安全工程、煤矿灾害预防、煤矿工作、煤矿分析、煤炭能源、煤炭行业等领域专业词汇，停用词典主要是去除分词处理后数据中存在的一些没有实际意义而词频较高的词。

以矿区的煤矿瓦斯爆炸事故案例为例，经过分词处理得到源于人、环境、机器以及管理等61项事故致因。煤矿瓦斯爆炸事故致因见表1，所提取事故致因符合《煤炭工业企业职工伤亡事故报告和统计规定》。

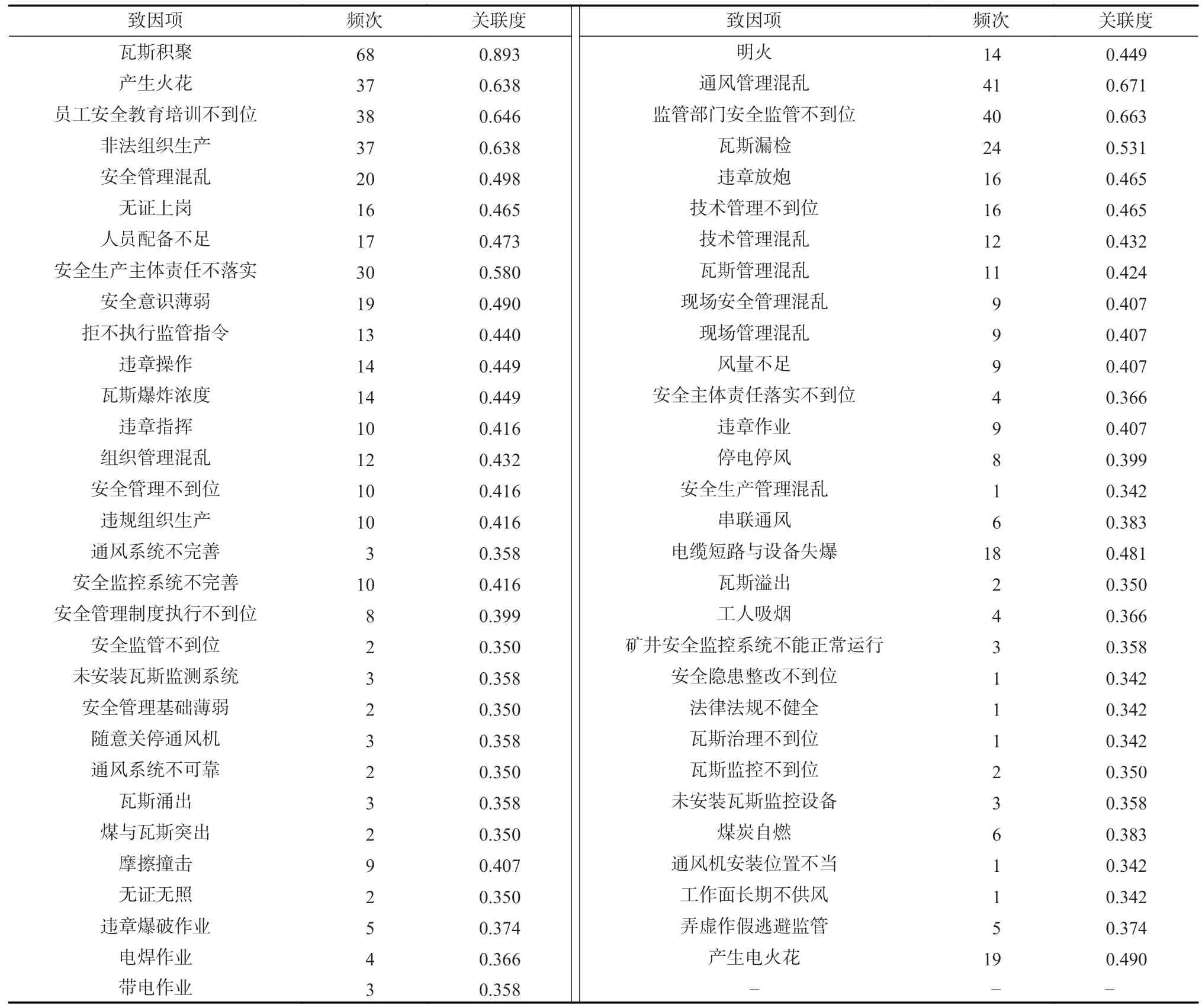
表1 煤矿瓦斯爆炸事故致因Table 1 Causes of gas explosion accidents in coal mines

鉴于事故致因条目过多，且不具备连续变量数值的特征，因而利用GRA 减少信息不对称性，降低维度，并通过量化关联度大小选取更符合实际情景的事故致因。

由于历史案例样本报告来源的不唯一性，因而设置状态标志位“0”“1”，1 条案例数据样本中对事故产生影响的事故致因设置为“1”，未产生影响的事故致因设置为“0”。煤矿瓦斯爆炸事故致因（F1～F6）状态设置见表2。

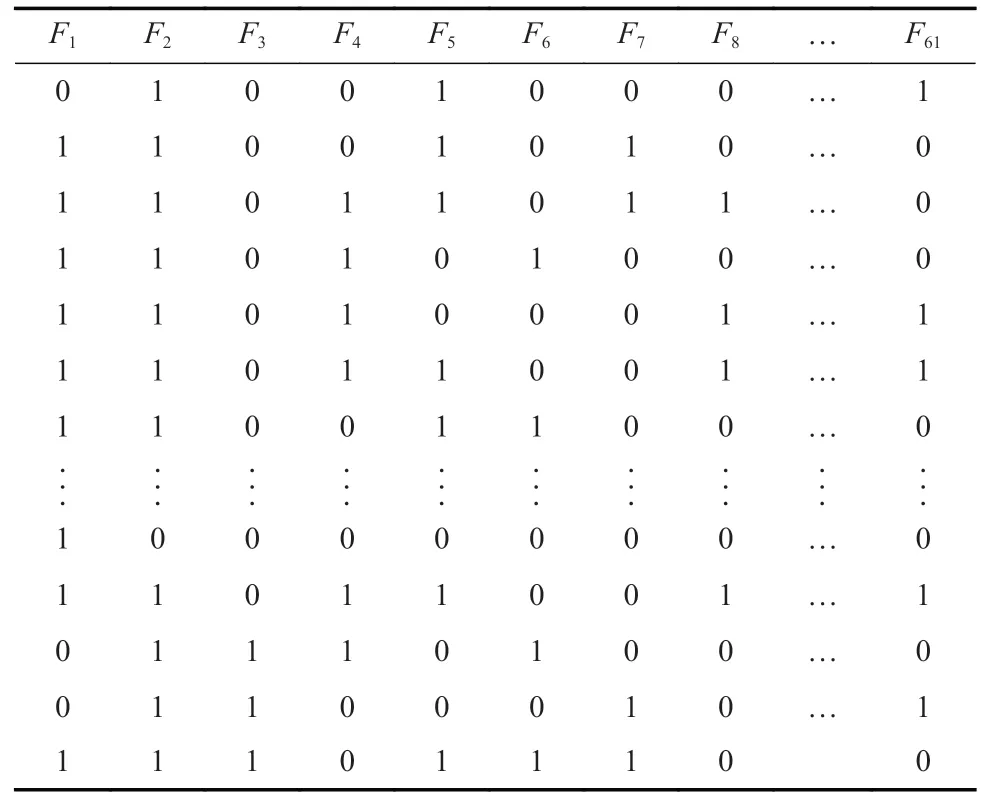
表2 煤矿瓦斯爆炸事故致因状态设置Table 2 Setting of the cause state of gas explosion accidents

对事故致因 Fi(i=1,2,···,61)与瓦斯爆炸事故等级的关联关系采用GRA 进行分析，分辨系数取值0.50，根据关联系数公式计算出关联系数值，关联系数计算如下：

式中：Fi(k)为 第i条 案例报告中第k项事故致因状态值；Y(k)为 第k条 案例报告中事故等级； ρ为分辨系数； ξi(k)为 在k条 记录Fi对事故等级的关联系数。

根据关联系数值计算出关联度值进行评价参考, 关联度计算如下：

式中：Ri为各事故致因与煤矿瓦斯事故之间的相似关联程度，由关联系数进行计算平均值得出。

关联度越大表示事故致因与煤矿瓦斯事故相关性越强。结合关联度大小，对所有事故致因进行排序，可以得到对煤矿瓦斯爆炸事故影响较大的事故致因，在此基础上结合煤矿的实际情景选取输入到PNN 网络中的特征向量。

3 瓦斯爆炸风险等级预测

3.1 预测模型设计

煤矿瓦斯风险等级预测是分析事故致因状态后预测风险存在的可能性，并将其按照风险等级的类别划分。PNN 总收敛于贝叶斯最优解，分类性能上与最优贝叶斯分类器等价，因而选用概率神经网络，将多种状态特征的事故致因做为预测模型的输入特征向量，进行瓦斯爆炸风险等级的分类预测。瓦斯爆炸风险等级预测模型如图2。

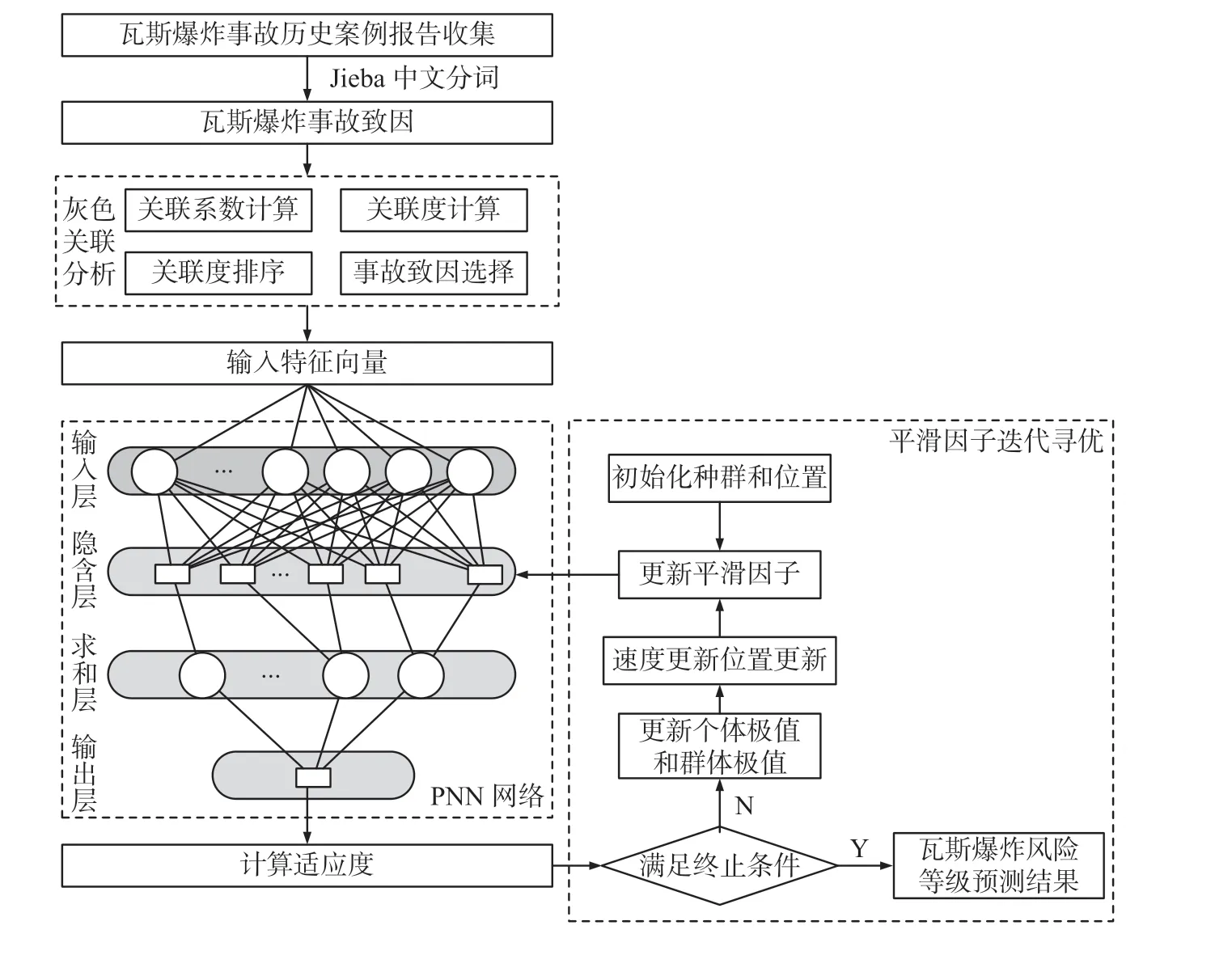
图2 瓦斯爆炸风险等级预测模型Fig.2 Prediction model of gas explosion risk grade

在PNN 中预设平滑因子 σ易造成模型识别率低、误分类等问题， σ取值需符合实际样本数据特征。RWPSO 能有效改善 σ仅凭经验取值所带来的缺陷，因而用其对PNN 的 σ取值进行迭代寻优，提高网络模型的预测准确率。

预测过程如下：

1）在瓦斯爆炸文本数据源中提取事故致因并采用GRA 选取模型输入特征向量。

2）采用RWPSO 对PNN 中的 σ进行迭代寻优，实现 σ的自适应调整。

3）结合最优 σ对瓦斯爆炸风险等级进行分类预测，得到最优的预测准确率。

选取网络实际输出与理论输出的总数比值作为模型的评价指标f，计算公式为：

式中：Y∗为网络实际输出与期望输出相同的样本个数；Y为网络实际输出的样本总数。

由于煤矿瓦斯风险事故致因特征包括数据类型多样，但数据表现形式仅为“0”“1”，因而模型可以拓展运用到数据样本具有连续数值特征的预测中，如：电动汽车故障诊断[12]、电网分区故障诊断[13]等领域中 。

3.2 基于随机权重策略的粒子群算法

RWPSO 随机选取惯性权重 ω，随机产生粒子历史速度对当前速度的影响。

若S维搜索空间内存在由n个粒子组成的群体X，X=[x1,···,xn]。群体中粒子速度和位置更新方式：

式中：c1、c2为学习因子；vis为当前粒子的变化速度；xis为当前粒子的变化位置；pis为当前粒子搜寻的最优位置；pgs为当前种群搜寻的最优位置； ω为随机选取惯性权重因子；r1、r2分别为0～1 之间的随机数。

ω更新公式如下：

式中： µ为权重因子； µmax、 µmin为权重因子的变化范围； θ为权重随机变化的大小；N(0,1)为标准正态分布的随机数； rand(0,1)为0～1 范围内的随机数。

通过引入 ω改善了种群在迭代初期局部搜索能力不足和后期全局搜索能力不足问题，提高了算法的收敛速度[14]。能有效应对PNN 中 σ的自适应调整。

3.3 RWPSO 迭代寻优平滑因子

PNN 网络中的隐含层用于计算输入数据与各模式的欧式距离， σ的取值直接影响瓦斯爆炸风险预测准确率。隐含层的输入/输出定义如式（7）。

式中： σ为平滑因子；d为样本维数；xi j为 第i类样本中第j个样本值。

PNN 中的 σ是Parzen 窗估计方法中高斯核带宽控制的参数，控制径向作用的范围，不同 σ的高斯核函数对样本数据映射范围如图3。

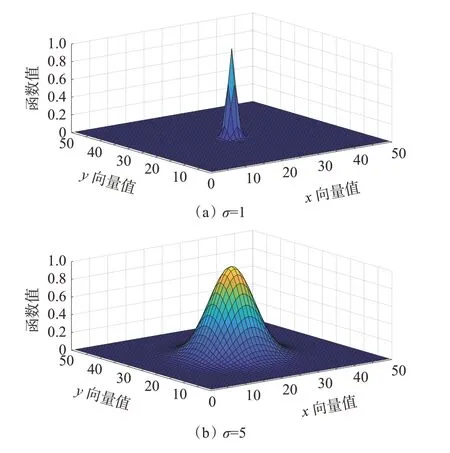
图3 σ对高斯核函数的影响Fig.3 The influence of σ on Gaussian kernel function

由图3 可以看出，高斯核函数的局部影响范围随着 σ取值的增大而增大。随机选取的 σ会引起PNN 不能正确判断远离输入样本的未知模式，容易引起网络识别率低等问题，从而影响瓦斯爆炸风险等级分类预测的准确率。因此实际样本训练中，需采用优化算法迭代选取适合当前训练样本数据的 σ。

RWPSO 优化PNN 中的 σ步骤如下：①初始化种群中各个粒子的vi和xi；②将网络模型预测准确率作为RWPSO 的适应度函数，选取最优适应度粒子的xi作 为种群的位置；③更新粒子的vi和xi；④计算粒子更新后个体的适应度，若更新后的适应度优于之前的个体适应度，则将更新后的适应度记为当前粒子的个体最优适应度；⑤若更新后粒子的适应度优于之前时刻种群所有粒子的适应度，则将更新后适应度记为当前种群的群体最优适应度；⑥判断是否满足终止条件，未满足返回步骤3，满足条件则输出最优解。

4 模型仿真

依据《煤矿生产安全事故报告和调查处理规定》将事故等级按照所造成的伤亡人数划分为：一般事故（对应输出值2）、较大事故（对应输出值3）、重大事故（对应输出值4）和特别重大事故（对应输出值5）。实验选取100 组数据进行验证，将70 组数据用作模型的训练样本，30 组数据用作模型的测试样本，取关联度在0.416 及以上的共27项事故致因作为特征向量对PNN 进行样本训练和测试，进行瓦斯爆炸风险等级的分类预测。当 σ值为1 时，PNN 的预测效果如图4。

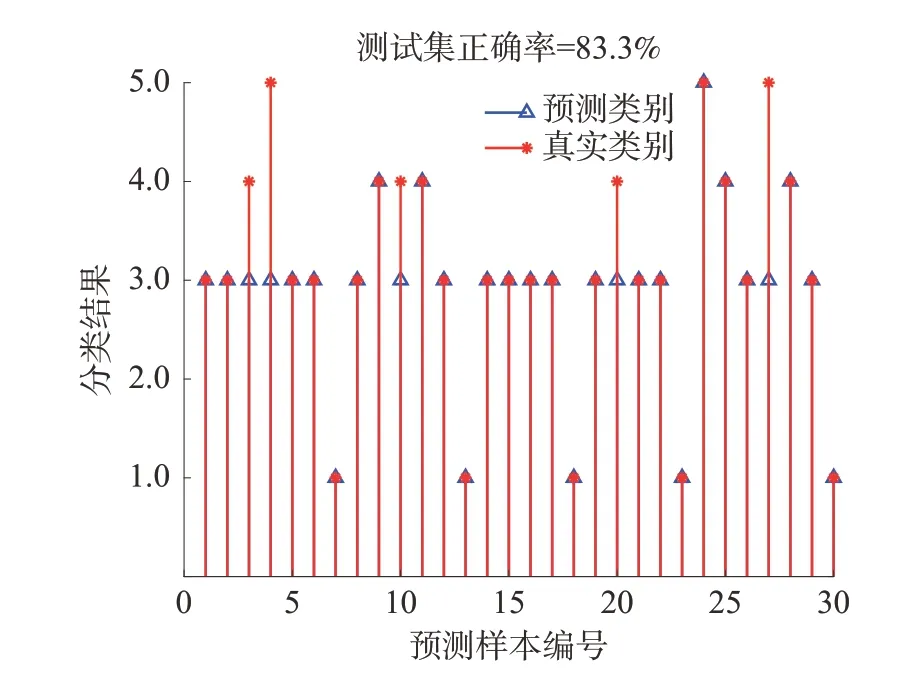
图4 PNN 预测效果Fig.4 PNN prediction effect

当选取 σ为1 时，预测准确率为83.3%，30 组测试样本中错误预测5 组，并且训练误差中出现负值，表明 σ选取较大。采用RWPSO 对PNN 的 σ选取进行优化，迭代次数选择为40，粒子个数为20，学习因子设置为2，优化后的预测效果如图5。

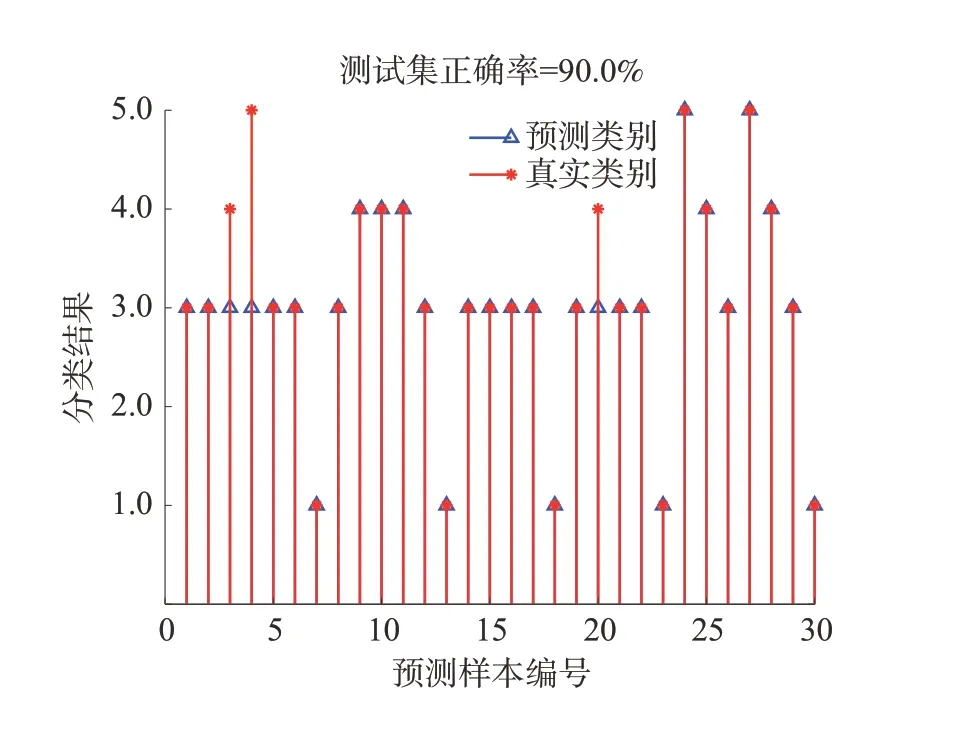
图5 σ优化后预测效果Fig.5 Prediction effect after σ optimization

此时 σ值为0.814，RWPSO-PNN 预测准确率为90.0%，30 组测试样本中错误预测3 组，有效实现分析事故致因状态后对瓦斯爆炸风险等级的分类预测，煤矿安全监管人员可根据模型预测的风险等级做出相应的安全防控措施。

PSO 算法的时间复杂度由迭代次数N和问题规模M共同决定，因而在N与M给定情况下，RWPSO与PSO 算法的时间复杂度为O(M∗N)，且RWPSO对随机初始种群参数进行了调节，提高了算法收敛速度，证明此算法满足实际应用需求。在实际应用过程中可对N与M进行调节，缩减算法运行时间，增加模型实用性。选取瓦斯爆炸预测中较为常用的BP 神经网络、极限学习机ELM、支持向量机SVM 算法作为对比算法，分别对煤矿瓦斯爆炸风险等级进行分类预测。RWPSO-PNN 与对比算法在煤矿瓦斯爆炸风险等级分类预测的准确率见表3。

表3 预测准确率对比Table 3 Comparison of prediction accuracy

由表3 知：RWPSO-PNN 错误预测为3 次，预测准确率达到90%，平均绝对误差（MAE）为0.133 明显优于对比算法。

5 结 语

根据煤矿瓦斯爆炸事故报告、案例以及知识体系选取多种状态的特征数据，作为煤矿瓦斯爆炸风险等级预测的事故致因，从多角度实现煤矿安全预警。基于RWPSO-PNN 建立风险等级的判定，使煤矿安全监察人员可以根据风险等级的预测制定相应的安全防控措施。预测模型中，利用随机权重策略改进粒子群算法后，迭代寻优平滑因子，有效实现概率神经网络中平滑因子的自适应调整。纵向对比常用的BP 神经网络、极限学习机ELM、支持向量机SVM 算法，实验结果显示RWPSO-PNN 在预测准确率高于其他算法。实验证明RWPSO-PNN 在煤矿瓦斯爆炸风险等级分类预测中的准确率更优。