求轨迹方程常用的方法

南广明

(甘肃省康县第一中学,甘肃 陇南 746500)

所谓求轨迹方程就是寻求动点坐标x,y之间的关系式. 解答这类题的关键是分析形成轨迹的动点和已知条件的内在联系,利用题设中的几何条件,用“坐标化”将其转化为寻求变量间的关系,选择最便于反映这种联系的形式,建立等式.

1 直接法

建立适当的坐标系后,设动点为(x,y),根据几何条件寻求x,y之间的关系式,此法称为直接法.

例1设A(-c,0),B(c,0)(c>0)为两定点,动点P到点A的距离与到点B的距离的比为定值a(a>0),求点P的轨迹.

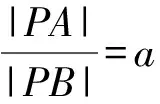
化简,得(1-a2)x2+2c(1+a2)x+c2(1-a2)+(1-a2)y2=0.

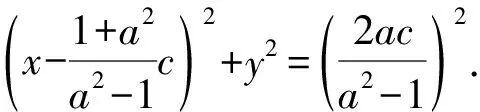
当a=1时,化简得x=0.

点评用直接法求出轨迹方程后,如果方程中有参数,要注意对参数的讨论,看其是否满足某种曲线对方程的特定要求.“轨迹”和“轨迹方程”是两个不同的概念,求轨迹方程只需要求出方程即可,而求轨迹则应先求出轨迹方程,再说明轨迹的形状.若题设条件有明显的等量关系,或者可运用平面几何的知识推导出等量关系,则可以通过“建系、设点、列式、化简、检验”五个步骤直接求出动点的轨迹.

2 定义法

如果所给几何条件正好符合已学曲线(例如圆、椭圆、双曲线、抛物线等)的定义,则可直接利用这些已知曲线的方程写出动点的轨迹方程,此法称为定义法.

例2 已知三点A(-7,0),B(7,0),C(2,-12),椭圆过A、B两点且以C为其中一个焦点,求此椭圆的另一个焦点的轨迹方程.

分析解答本题可先根据椭圆的第一定义,再考虑另一个焦点的几何特征即可解决.

解析设另一个焦点为M(x,y),则根据椭圆的定义,有|AC|+|AM|=|BC|+|BM|.

所以|MB|-|MA|=|AC|-|BC|=2.

又|AB|=14>2,所以|MB|-|MA|<|AB|,即动点M的轨迹是以原点为中心,A,B为焦点,实轴长为2的双曲线的左支.

点评求曲线的轨迹方程时,尽可能地利用几何条件探究轨迹的曲线类型,从而再利用待定系数法求出轨迹的方程,这样可以减少运算量,提高解题的速度与质量.在用双曲线的定义时,应特别注意定义中的条件“差的绝对值”,弄清所求轨迹是整条双曲线还是双曲线的一支,若是一支,则是哪一支?以确保轨迹的纯粹性和完备性.

3 参数法

当动点P(x,y)坐标之间的关系不容易直接找到,也没有相关信息可用时,可考虑将x,y均用中间变量(参数)表示,得参数方程,再消去参数,得到动点轨迹的普通方程,此法称为参数法.

分析设G(x,y),∠AOB=θ,首先表示B,C两点坐标,再利用重心坐标公式列参数方程,消去θ即得点G的轨迹方程.

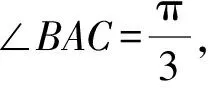
由重心的坐标公式,得点G的坐标为

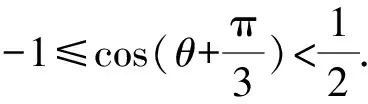
故所求的轨迹方程为

点评本题是与角有关的轨迹问题,显然可以用参数法来求解,在引入参数时要考虑参数的取值范围.

4 代入法(相关点法)

利用所求曲线上的动点与已知曲线上动点的关系,把所求动点转换为已知动点.具体地说,就是用所求动点的坐标(x,y)来表示已知动点的坐标,并代入已知动点满足的曲线方程,由此可求得动点坐标(x,y)满足的关系,此法称为代入法.

例4 从双曲线x2-y2=1上一点Q引直线l:x+y=2的垂线,垂足为点N,求线段QN的中点P的轨迹方程.

分析设P(x,y),因为P是QN的中点,为此需用点P的坐标表示点Q的坐标,然后代入双曲线方程即可.

解析设点P的坐标为(x,y),双曲线上点Q的坐标为(x0,y0).因为点P是线段QN的中点,所以点N的坐标为(2x-x0,2y-y0).

又点N在直线x+y=2上,

所以2x-x0+2y-y0=2.

即x0+y0=2x+2y-2.

①

即x0-y0=x-y.

②

由①②,得

又因为点Q在双曲线上,

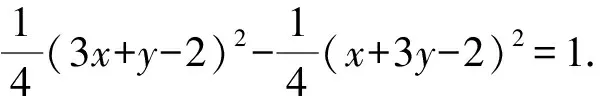
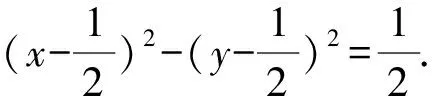
所以线段QN的中点P的轨迹方程为

点评本题中动点P与点Q相关,而点Q的轨迹确定,故解决这类问题的关键是找出P,Q两点坐标间的关系,用相关点法求解.

5 交轨法

在求动点轨迹方程时,经常会遇到求两动曲线的交点的轨迹方程问题,我们先列出两动曲线的方程,再设法消去曲线中的参数即可得到交点的轨迹方程,此法称为交轨法.

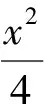
分析与y轴平行的直线设为x=x1,点P和P′的纵坐标设为y1和-y1,写出直线AP和A′P′的方程,可以求其交点,再利用点(x1,y1)在椭圆上,消去x1,y1即可得到轨迹方程.

①

当x1≠±2时,直线AP和A′P′的方程分别为

②

③

因为交点Q满足②③,由②×③得

④

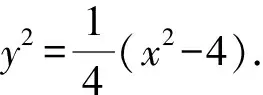
⑤

当x1=±2时,y=0,满足⑤,

点评本题是用交轨法求得轨迹方程的.如果所求轨迹是由两条动曲线(包括直线)的交点所得,其一般解法是恰当地引进一个参数,写出两条动曲线的方程,消去参数,即得所求的轨迹方程.

6 几何法

根据曲线的某些显著的几何特征和性质,通过推理列出等式求出轨迹方程,这种求轨迹的方法叫做几何法.

分析利用三角形外心的性质及含30°角的直角三角形的性质求解.

点评借助于平面几何的有关定理、性质等,从而分析出其数量关系,这种借助几何定理的方法是求动点轨迹的重要方法.

7 待定系数法

凡是已知曲线类型,只需利用已知条件,求出曲线方程中的待定系数就可以求出曲线方程,这种求轨迹的方法叫做待定系数法.

例7 已知圆C在x轴上的一个截距为-2,在y轴上的截距为1和3,求圆C的方程.

点评求解本题的关键是根据已知条件判断出所求圆过三点的坐标.

8 设而不求法

求弦的中点的轨迹方程,常常运用“设而不求”的技巧,通过中点坐标及斜率的代换,达到求出轨迹方程的目的[1],这种求轨迹方程的方法叫做设而不求法,也称做“平方差法”“点差法”“差分法”等.

分析利用弦的两端点P(x1,y1),Q(x2,y2)在已知的二次曲线上,将P,Q的坐标代入方程,然后相减,利用平方差公式可得含x1+x2,y1+y2,x1-x2,y1-y2的关系式,再利用其他条件代入整理即可得到轨迹方程.

两式相减,得

又因为x1+x2=4,y1+y2=2,

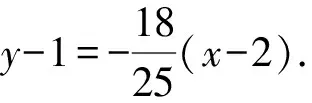
即18x+25y-61=0.

点评设而不求法求轨迹方程的步骤:(1)设点;(2)代入;(3)相减;(4)求解.运用此法要注意限制轨迹方程中变量可能的取值范围.