整体视角巧切入 数形结合妙求解——三角函数中ω的求解思考

陈丽洪

(福清第三中学,福建 福州 350315)

三角函数是高中数学内容中非常重要的模块.由于三角函数涉及的知识点丰富,题型灵活多变,所以很多学生对此类问题存在畏惧心理.特别是以ω为参数的三角函数试题不仅是数学高考的热点,也是难点,在很大程度上困扰着学生.

利用整体思想和数形结合等数学思想,把复杂问题简单化、熟悉化,能更有效地破解求参数ω的问题.实践表明,学生在用整体思维解答三角函数问题时,被其中所蕴含的巧妙所折服.而数形结合思想,可以把抽象的问题可视化,极大地简化计算,使我们更快地抓住问题的本质.所以,在解三角函数有关问题时,我们应该将两种思想结合使用.

1 试题呈现

设计意图本题考查正弦函数的单调性和最值,以及正弦函数的图象特征,兼顾考查了学生直观想象、逻辑推理、数学运算等核心素养以及转化与化归等重要数学思想,同时还考查了学生分析问题、解决问题的能力.

2 解法分析

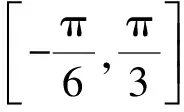
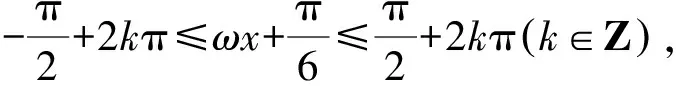
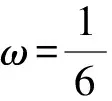
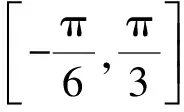
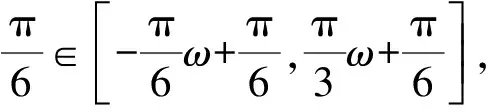
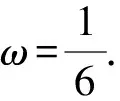
3 方法剖析

4 应用赏析

例1已知函数f(x)=cosωx-1(ω>0)在区间[0,2π]有且仅有3个零点,则ω的取值范围是____.

命题意图本题考查余弦函数图象和零点问题,侧重考查逻辑推理、数学运算的核心素养.

分析由零点的定义,令f(x)=0,得cosωx=1有3个解,然后利用整体代换化熟悉和数形结合定区间两个步骤并结合余弦函数的图象性质即可得解.

解析因为0≤x≤2π,所以0≤ωx≤2ωπ.

令f(x)=cosωx-1=0,则cosωx=1有3个根,令t=ωx,则cost=1有3个根,其中t∈[0,2ωπ],

由图1可得4π≤2ωπ<6π,故2≤ω<3.

图1 y=cost图象

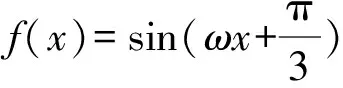
解析依题意可得ω>0.

图2 例2解析图

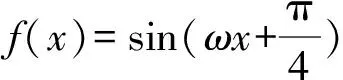
此题与前面一题的主要区别是不能直接判断区间大致位置,此时可根据三角函数图象特征,也就是“单调区间长度不超过半个周期”,首先得到ω的大致取值范围,从而确定区间两端点的取值范围,接着再结合图象与性质确定区间左右端点的具体范围,从而求出ω的取值范围.

数学思想是对数学相关概念、定理等内容最本质的认识,《数学课程标准(2017年版2020年修订)》指出:数学学科核心素养是“四基”的继承和发展[2].“四基”是培养学生数学学科核心素养的沃土,是发展学生数学学科核心素养的有效载体.而数学思想方法是“四基”的重要组成部分,因此,教师应有意识地在日常教学中渗透数学思想方法,以提高学生的数学思维水平,提升素养为目标,促使学生更好地适应考试题目的创新.