一道2023年竞赛试题的解答与推广

马 岚

(江苏省盐城市实验高级中学,江苏 盐城 224006)

2023年上海市数学竞赛的第11题是一道以三角形为背景的最值问题,主要考查正弦定理、余弦定理、辅助角公式、直线方程、复数、平面几何等相关知识.试题简洁且内涵丰富,很有新意,值得探究.本文呈现其解法,并给出推广结论,供大家参考.

1 题目的呈现与解法探究

题目给定Rt△ABC,其中∠ACB=90°,BC=a,AC=b,点D,E,F分别在边BC,CA,AB上,使得△DEF是正三角形,求△DEF面积的最小值.

解法1 如图1,设∠CDE=θ,△DEF的边长为x,则BD=a-xcosθ,∠BDF=120°-θ,∠BFD=60°+θ-B.

在△BDF中,由正弦定理,可得

评注解法1应用正弦定理,结合辅助角公式,利用正弦函数的有界性进行放缩,求出△DEF边长的最小值,从而求得其面积的最小值.这种解题思想是三角形中有关最值问题的常用思路.

解法2如图2,以C为坐标原点,CB为x轴,CA为y轴建立平面直角坐标系,则A(0,b),B(a,0).

设△DEF的边长为t,∠FDB=θ,则∠EDC=120°-θ.

于是F(tcos(120°-θ)+tcosθ,tsinθ).

图2 解法2示意图

即bx+ay-ab=0.

由于点F在直线AB上,所以

btcos(120°-θ)+btcosθ+atsinθ-ab=0.

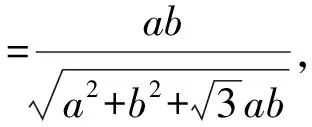
评注解法2利用△ABC是直角三角形,以C为坐标原点建立坐标系,使得点A,B落在坐标轴上,并容易求得直线AB的方程,再用点F在直线AB上求解△DEF边长的最小值.解法2的思维难度与运算量要比解法1小,且过程简洁.解三角形与解析几何的结合能增强知识之间的融会贯通,拓展知识面,对提高解题能力具有重要意义.

解法3如图2,以C为坐标原点,CB为x轴,CA为y轴建立平面直角坐标系,则A(0,b),B(a,0).

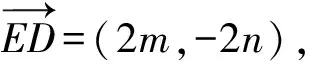
因为|ED|=|EF|,且∠DEF=60°,

z2=z1(cos60°+isin60°)

=(2m-2ni)(cos60°+isin60°)

即bx+ay-ab=0.

由于点F在直线AB上,所以

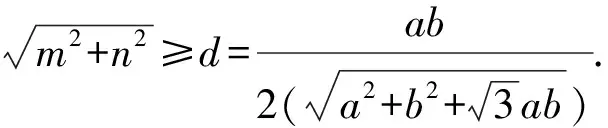
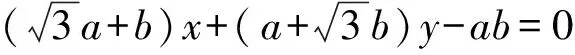
解法4如图3,作△BDF的外接圆,作GB⊥BC,并交圆于点G,连接GD,GE.

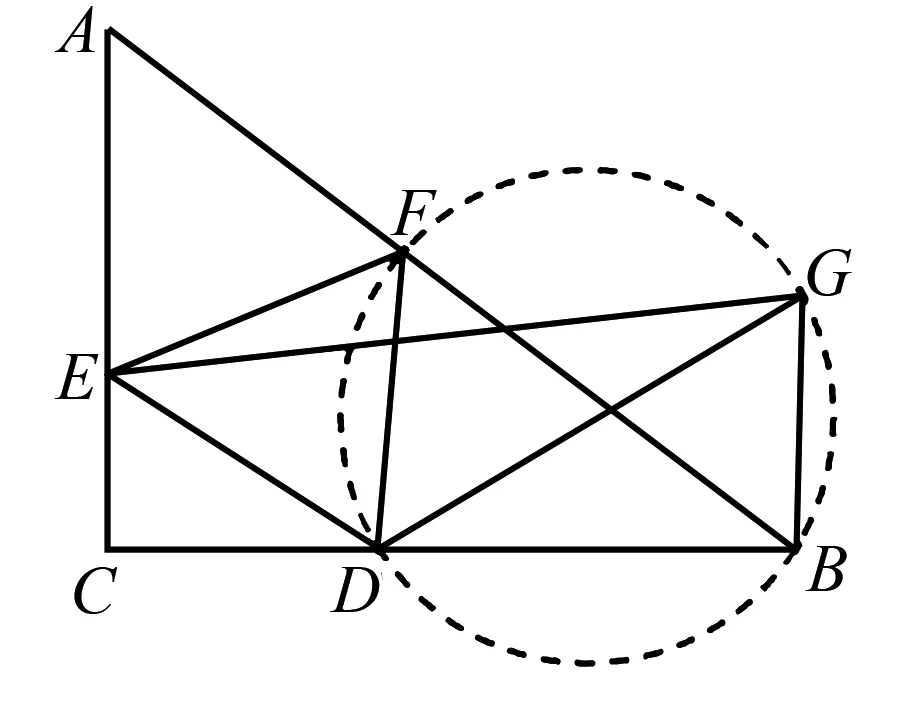
图3 解法4示意图

因为∠GBD=90°,

所以GD是△BDF外接圆的直径.

又因为∠DBF+∠GBF=∠DBF+∠A=90°,

所以∠GBF=∠A.

即得∠GBF=∠GDF=∠A.

于是∠GDE=∠A+60°.

设△DEF的边长为x.

在△BDF中,由正弦定理,得

在△GDE中,由余弦定理,得

GE2=DG2+DE2-2DG×DEcos(A+60°)

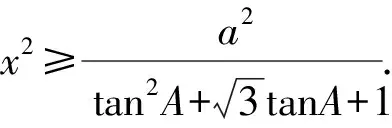
评注解法4利用平面几何性质,结合正、余弦定理求解,简化了推理和运算过程,具有直观、简捷的特点.解三角形问题的本质是几何问题,如果能恰当利用平面几何知识,往往可以避开繁琐的代数运算,使解决问题的过程得到简化[1].

2 试题的推广

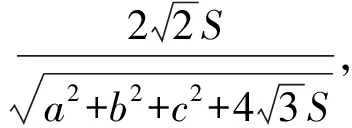
证明如图4,设正△DEF内接于△ABC,点D,E,F分别在边BC,CA,AB上.设∠BFD=θ,则易得∠DEC=∠A+60°-θ,设△DEF的边长为x.

图4 推广结论示意图

在△DEC中,由正弦定理,得

又因为BD+DC=BC=a,故

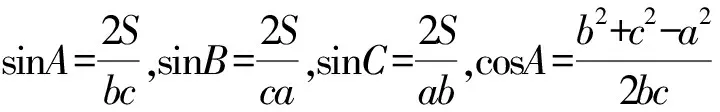
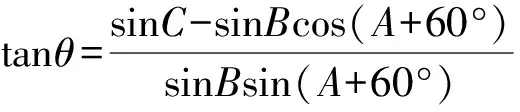
前述的几种解法,从不同的思维角度解答问题,各显神通.学数学离不开解题,同时要注意的是,数学问题的解决仅仅只是一半,更重要的是在解题中要善于观察、善于思考、善于转化,只有这样才能将零散的数学知识串联起来,运用自如.