基于地铁车辆全生命周期健康状态的维修策略研究

吴 亮，徐 炬，何兴家，潘 越

（杭州地铁运营有限公司，浙江杭州 310017）

0 引言

在地铁行业信息化发展过程中，相关业务系统产生了大量的基础数据，这些数据既是地铁车辆维护管理和运营决策的重要支撑，也是相关科研工作的重要依据。但在日常运维工作中仅靠人工统计无法高效利用这些数据。因此，结合大数据及人工智能的时代背景，运用可靠性分析、FMEA（Failure Mode Effects analysis，失效模式及后果分析）等方法实现基础数据处理，以PHM（Prognostic and Health Management，故障预测和健康管理）为依托，探索地铁车辆全生命周期健康状态管理，量化维修决策，实现“状态修”。

1 地铁车辆全生命周期健康状态评价

1.1 部件可靠性分析

根据FMEA，按照功能、故障模式、故障原因及补偿措施将各子系统进行部件分解，以车门系统作为分解对象进行FMEA 分析，分解为承载导向装置、基础部件、电动控制装置、内外操作隔离装置、驱动锁闭装置四部分，分解表格形式见表1。

表1 车门系统FMEA 分析——内外操作隔离装置（例）

1.2 子系统可靠性分析

根据FMEA 分解结果，计算各子系统可靠性。使用故障率进行子系统可靠性分析，产品故障率λ（t）：

式中 Δr（t）——t 时刻后，Δt 时间内发生故障的产品数

Δt——所取时间间隔

NS（t）——在t 时刻没有发生故障的产品数

将各系统2018—2020 年度故障数、运行次数代入式（1）,计算得出2018—2020 年度各系统故障率，求平均值作为该系统最终故障率，即可靠性（图1）。

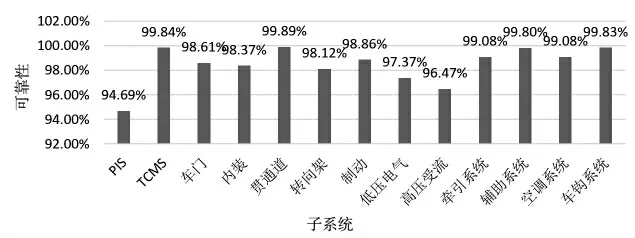
图1 杭州地铁4 号线地铁车辆2018—2020 年度各系统可靠性

2 地铁车辆健康状态诊断

2.1 AHP（The analytic hierarchy process，层次分析法）层次分析建模

2.1.1 建立AHP 层次结构

对地铁车辆的健康状态进行层次划分，建立地铁车辆健康状态评价模型，包括目的层——地铁车辆健康状态，准则层——故障影响程度、子系统运行情况，以及方案层——地铁车辆各系统专家评分，如图2 所示。

图2 层次结构示意

2.1.2 建立比较矩阵

以故障影响程度、子系统运行情况为准则，分别比较方案层地铁车辆各系统的影响程度，得到判断矩阵C，用影响程度cij表示第i 个要素与第j 个要素相比的重要程度。且矩阵C 需要满足：①影响程度cij>0；②第i 个要素与第j 个要素影响程度的比值互为倒数；③同一要素相比，重要程度相同cii=1，其中i、j=1，2，…，n。

影响程度cij的取值需要满足表2 要求。

表2 影响程度cij 的取值要求

2.1.3 检验一致性

明确后，在求出判断矩阵C 的最大特征值λmax后，代入式（3）求出13 阶判断矩阵C 的CI 值：

然后计算13 阶判断矩阵C 的随机一致性比率：

其中，CI 为判断矩阵C 的一致性指标。

判断矩阵C 是否有较好的一致性，可比较CR 与0.1 的大小，当CR＜0.1 时，矩阵C 具有较好的一致性，否则矩阵的一致性不良，应重新修改后再次检验，直到调整至CR＜0.1。

2.1.4 权重计算

使用求和法进行判断矩阵C 各元素的权重计算，具体步骤如下：

（1）对矩阵C 的每一列元素按式（5）进行归一化：

（2）完成归一化后，各列按式（6）计算每列和，构成一个向量：

本文中，矩阵阶数n 取13，i=1、2、3…13。

2.2 地铁车辆健康状态建模——以2019 年杭州地铁4 号线地铁车辆故障数据为例

结合地铁车辆实际运营情况，选用故障影响程度、各子系统运行情况作为第一层因素建立地铁车辆健康状态评价模型。

2.2.1 建立评价因素集（表3）

表3 评价因素

2.2.2 确定各层因素的权重

根据地铁车辆故障影响程度和子系统运行情况与各系统的联系，对地铁车辆各系统的重要程度设置相应的数值，然后以此计算各指标影响地铁车辆整体健康状态的权重值。

（1）评估指标专家打分。首先，请杭州地铁4 号线地铁车辆各专业检修工程师根据经验进行打分。为避免由一名工作人员打分过于主观，通过将评估指标两两对比，减少评分人员主观性，使评分结果更具有真实性。评估指标打分表见图3。

图3 评估指标打分表

（2）特征根和权重向量的计算。按照层次分析建模的计算步骤，计算权重∂的权重向量为：∂=[0.020，0.059，0.038，0.183，0.192，0.057，0.103，0.133，0.066，0.031，0.077，0.019，0.019]，求解特征根：

（3）权重一致性检验。权重一致性：

通过一致性检验可知，判断矩阵C 可作为计算依据，用于地铁车辆健康状态评价模型的权重计算及模型构建。

最后，完成模型的权重计算，计算结果见表4。

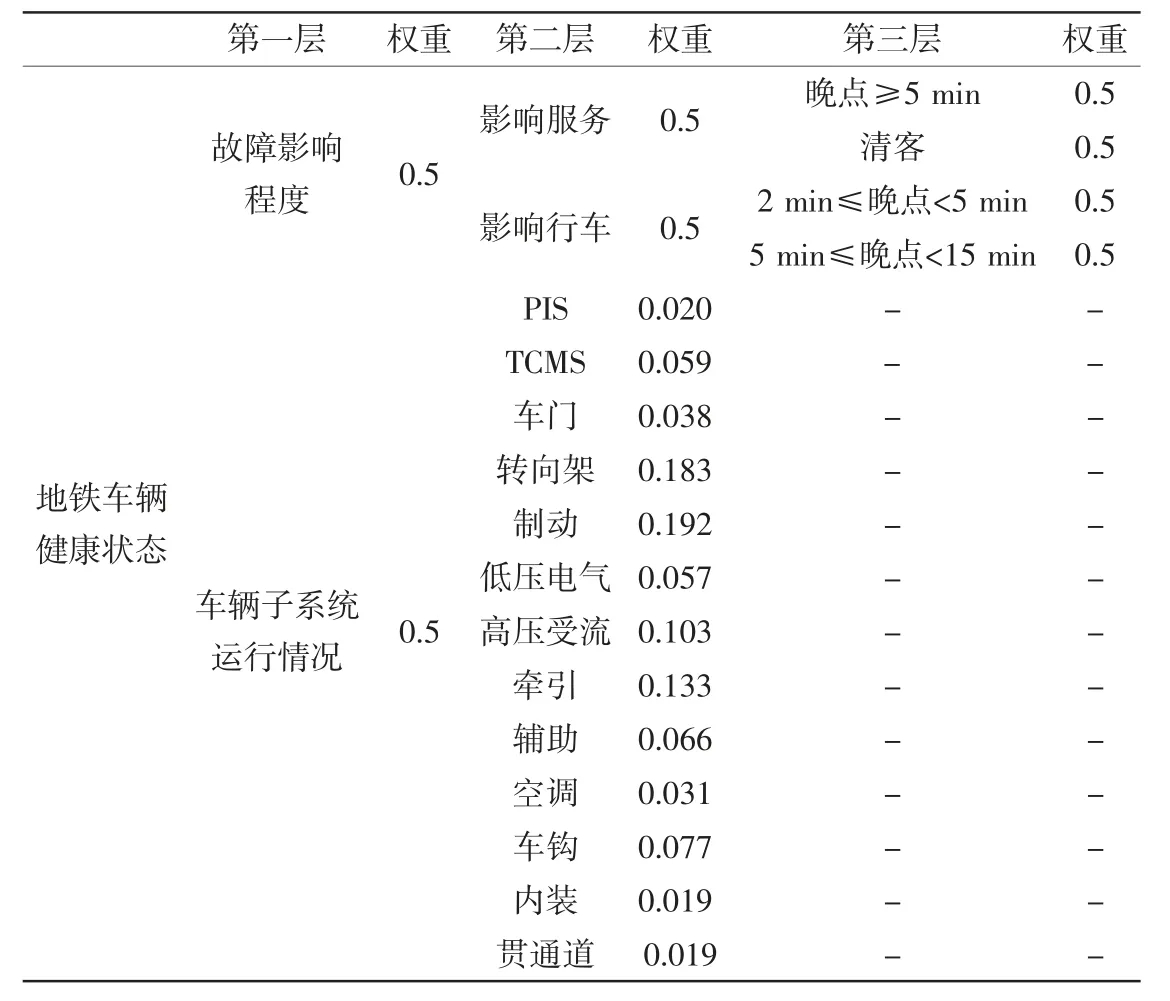
表4 评价因素权重

2.2.3 杭州地铁4 号线算例分析

根据杭州地铁4 号线2019 年故障数据进行算例分析，表5 为2019 年4 号线各系统故障数据。

表5 杭州地铁4 号线2019 年故障数据

根据表3 数据可得2019 年各个系统的故障率（表6）。

表6 杭州地铁4 号线2019 年各系统故障率

根据以上数据，首先建立故障影响程度、子系统运行情况（故障率）的评判集。同时以K04001 车故障率数据为例，采用加权平均型模型进行计算，评价结果根据因素集中所有给出权重的因素的影响。

为更加客观地评判地铁车辆健康状态，建立评判集V={V1，V2，V3，V4}，对应优、良、中、差4个等级。见表7、表8。

表7 故障影响程度评判集

表8 子系统运行情况评判集

表9 地铁车辆健康状态评价模型评判集及取值范围

结合故障影响程度、子系统运行情况（故障率）的评判集综合考虑，确立地铁车辆健康状态评价模型的评价集及取值。

同时确定各指标ui隶属于评价等级的隶属度rij，采用专家评分法确定隶属度rij，可得到故障影响程度的第二层评价因素隶属度R1，车辆子系统运行情况的第二层评价因素隶属度R2。

地铁车辆健康状态等级的隶属度计算：

其中“O”取算子M(·，+)：a·b=a×b=ab；a+b=a+b。（a1，a2）为第一层因素的权重系数。

按照最大隶属度原则，该车健康状态良好，通过计算最终得到K04001 车2019 年综合评价结果为93.629 分（表10）。

表10 K04001 车2019 年故障率数据及综合评价结果

3 地铁车辆维修决策优化

城市轨道交通具有早晚客流高峰时间段且夜晚不运营的特点，车辆存在停止运营的间隙时间，又称作列车的运行“窗口”（图4）。为了有效提高检修工作效率，利用地铁车辆停运窗口时间，将检修作业分散在窗口时间，利用计算得到的地铁车辆健康状态结果，继续采用层次分析理论，提高“窗口”时间的利用率。

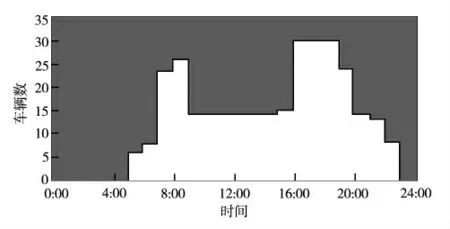
图4 列车运行“窗口”

杭州地铁现行的检修模式为均衡修作业，但各检修项目频次、标准较为统一，结合列车运行“窗口”的特点，综合各系统维护要求、实际故障发生率、检修情况等，参考地铁车辆健康状态将数据，动态均衡修作业标准，从而实现从计划修到状态修的转变，提高列车上线率。设立与评判结果相对应的检修级别，分别为Ⅳ、Ⅲ、Ⅱ、Ⅰ，车辆健康状态越佳，其检修评级越低，相应对应的作业时间也越低。

为确定检修评级，本文选用2019 年杭州地铁4 号线所有（29列）地铁车辆健康状态数据集为划分依据（表11），采用统计学等距分组的原则，将所有分数排序后分组建立健康状态评级标准（图5）。

图5 2019 年4 号线地铁车辆健康状态分组

其对应关系和检修计划的时间如表13 所示。

完成对应关系体系建立后，可按照车辆得分给出作业时间建议。取用杭州地铁4 号线K04001 车健康状态评级进行该车均衡修1 作业时间优化，由表11 可知，该车2019 年最终健康状态得分为93.629 分，按照评价等级（表12），该车为“优”等级，对应表13 可知，K04001 车2020年均衡修1 作业检修评级为Ⅳ级，建议安排作业时间为5～6 h，相比较没有做健康状态评估的检修计划的8 h，检修的时间缩短了2～3 h，提高车辆的运营时间，从优化检修计划层面进一步提升车辆上线率。

4 总结

本文采用PHM 管理理念，首先利用FMEA 进行地铁车辆各子系统功能、故障模式、故障原因及补偿措施况的定型分析，确定系统可靠性。之后，基于系统可靠性，运用AHP 分析建立地铁车辆健康状态模型，量化评估地铁车辆全生命周期健康状态。最后，根据地铁车辆全生命周期健康状态建立对应检修评级及作业时间对应关系，给出作业时间建议，实现维修决策优化，最终实现地铁车辆从故障修到状态修的转变。