基于改进的五行环算法的移动机器人路径规划
黄敬尧,刘洪宇,武慧慧,王钦甜
(三峡大学 电气与新能源学院,湖北 宜昌 443002)
0 引 言
路径规划是移动机器人的热门研究之一,随着科技的进步和社会的发展,移动机器人智能化和自动化的水平逐步提高,已经逐渐渗透到日常的生活中[1]。移动机器人需要规划出从工作环境的起点位置到目标位置的路径,并且满足效能高、安全性高等要求,还必须能够避开沿途的障碍物。移动机器人的路径规划具有重要的研究意义和价值,国内外学者已将其作为研究热点。
作为智能搜索法的遗传算法(genetic algorithm,GA)、蚁群算法、粒子群优化(particle swarm optimization,PSO)算法等算法,可以通过随机的可行初始解出发以及迭代改进的策略,不断地逼近最优路径,从而求出最优解。杨洋等人针对多自动导引运输车(automated guided vehicle,AGV)避障路径优化问题,提出一种改进蚁群算法和弹性时间窗相结合的多AGV避障路径优化策略[2]。不仅能在无人仓库中实现多AGV快速规划,同时还能找到最优的躲避障碍物的路径。罗阳阳等人针对PSO算法能快速收敛,但容易陷入局部最优的问题,设计了一种突变算子来提高全局寻优能力[3]。虽然迭代次数会大幅增多,但其需要调节的参数较少,在更新机制中仅需要追踪2 个“极值”来进行不断的更新,也是很有可取之处的。
本文提出一种改进的五行环算法来解决机器人路径规划问题。在五行环模型的基础上,采用PSO算法的更新机制来对元素进行更新。为了避免过早出现的较优解使得种群陷入局部最优解陷阱,采用变异的思想,设计了突变元子。为了避免种群快速趋同而降低元素的搜索效率,设计了散开元子。最后对路径进行连接点删除,删除了不必要的连接点,使得路径更优。通过仿真结果表明,采用改进的五行环算法能够使移动机器人找到最优路径的同时具有高度的稳定性,也证明了算法改进的可行性和有效性。
1 问题描述与环境建模
本文将环境映射为栅格地图,即将环境转化为由相同大小格子构成的一个栅格矩阵[4,5]。对每个栅格以实数进行编码,将实际障碍物对应的栅格以0填充,在地图中以黑色表示,对可行区域以1 填充,以白色表示。本文采用20 ×20和30 ×30的两种栅格地图,如图1 所示。每个栅格的边长为1,其中机器人的起始点与目标点都已标明。
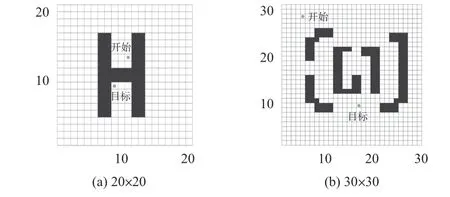
图1 环境模型
2 改进五行环算法的移动机器人路径规划
2.1 五行环模型
五行环模型[6]是建立在五行(金、水、木、土、火)相生相克原理的基础上,通过计算各个体之间的相互作用关系如图2,比较出个体适应值的优劣,然后来对解进行更新,从而找出系统的最优解。

图2 五行元素相互关系
从图2中可以看出,5种元素之间,由相生关系和相克关系建立了各个元素之间的关系,既相互促进又相互克制,形成了一个复杂的动态平衡[7]。为了将其应用到各种复杂的优化问题,文献[8]提出了五行环算法,并且将它推广到了一般形式,其一般表达式为
式中 mij(t)为第t 代中第j 个环中第i 个元素的质量,Fij(t)为元素的力。假设复杂系统中总共有h 个环(j =1,2,…,h),y个元素(i =1,2,…,y),则种群的规模为h×y。
在五行环模型中,每个环中的元素Fij(t)都由4 个部分的力组成:1)上辈元素的“生”力:若上辈元素的质量大于元素本身的质量,则此部分力为正值,反之力为负值。2)祖辈元素的“克”力:其力本身为负值,若元素本身的质量大于其祖辈元素的质量,则力变为正值。3)本元素对子元素的“生”力:这部分力会使自身能量产生损耗,因此为负值。4)本元素对祖辈元素的“克”力:同样在施加力的过程中消耗了自身的能量,因此其力也为负值。式(1)中质量的表达采用的是logsig 函数,其用来表示在力的作用下质量的变化。其中,i =1 时,用y 替代i -1,用y -1 替代i-2;i =2时,用y替代i-2;i =y-1时,用1替代i +2;i =y时,用1替代i +1,用2替代i +2。
2.2 路径规划
2.2.1 PSO算法
在PSO算法中,群体中所有个体都被抽象为在d维空间中无重量和体积的粒子,并在搜索空间中以不同的速度飞行[9]。粒子在飞行时,通过追踪2 个“极值”来不断地更新自己的速度和位置,一个是全局极值,一个是个体极值[10],其更新的速度和位置公式如下
2.2.2 突变元子[13]
具体突变方式是:先将实数编码转换为二进制编码,再随机生成一个整数(不能大于有效编码的总长度的整数值)作为突变连接点的个数,然后在编码区内随机确定突变的连接点位置,在突变位置上对该连接点进行突变(将1→0,0→1),最后将其转化为实数编码。
2.2.3 散开元子
为了减轻元素快速趋同带来的不利影响,本文设计了散开元子[14]。对搜索空间中处于某一位置上的多个相同的元素仅保留一个,而对其余的元素进行突变使其离开原来的位置,突变方法和2.2.2节一致。如图3 所示,在某一搜索空间中,如果同时聚集了3 个以上的元素,则元素A保持不变,其余元素被移至其他的位置;如果聚集了不到3个元素,则允许它们都保留在原位。

图3 散开元子示意
2.2.4 改进的五行环算法
1)更新机制
通过对Fij(t)的计算,可以将结果分为Fij(t)>0 和Fij(t)≤0两类。若Fij(t)>0,则采用式(2)的更新机制对元素群进行更新,并使用散开元子避免出现快速趋同的现象;若Fij(t)≤0,则xij(t)使用突变元子更新。
2)mij(t)变化规则
在使用五行环模型时,采用xij(t)表示第t代中第j个环的第i个元素的解,即xij(t)表示一条可行路径,而S 表示搜索连接点的总个数。用(xd,yd)表示第d 个连接点的坐标,d =1,2,…,S,重新定义mij(t),mij(t)表示一条可行路径的欧氏距离,其表达式为
式中 κ为缩小因素。
3)适应度函数
每个元素的适应度函数[15]表达式为
改进的五行环算法具体步骤为:1)初始化参数,随机生成种群。2)通过式(1)计算mij(0)。3)通过式(1)计算Fij(t),根据结果采用不同的更新机制。4)计算各个元素群的适应度值,并通过式(3)计算mij(t +1)。5)如果没达到最大迭代次数T,则令t =t +1,继续返回进行步骤(3);如果达到最大迭代次数T则结束整个流程。
2.2.5 连接点删除[16]
图4为连接点删除的简单示意,黑色虚线为连接点删除之前的路径,浅色实线为删除连接点之后的路径。

图4 连接点删除示意
3 仿真与分析
对比了五行环优化算法、PSO算法、GA和A*算法,并分别置于2种不同栅格环境的2种不同复杂度的地图中进行路径规划,并进行仿真与比较分析。图5 是栅格环境为20 ×20的简单和复杂地图(障碍物覆盖率为30%)不同算法的路径规划。仅展示不同地图的改进五行环算法、五行环优化算法和PSO算法3种算法的路径规划。

图5 不同复杂度地图的20 ×20 机器人路径规划路线
从图5中可以明显观察到,当3 种算法不论是在简单地图还是在复杂地图中规划的最优路线中,五行环优化算法能用较短时间规划出一条路径,但其稳定性极差,局部搜索能力不强,规划出来的路径较长。PSO 算法在进行路径规划时极其容易陷入局部最优解的陷阱中,搜索时间较长,收敛效果较差。而本文改进的五行环算法规划出的路径轨迹最为平滑,拐点数目明显少于其他算法,能在短时间内规划处最短的无碰撞的路径。
表1为各算法在20 ×20 栅格环境不同复杂度地图的路径规划数据,设每个栅格边长1 cm。

表1 5 种算法的数据比较(20 ×20 地图)
从表1中数据可得,A*算法在路径规划中的路径长度是最长的;GA和PSO算法总体上稳定性较高,但有少数波动情况,导致平均路径大于最短路径,拐点数目也较多;五行环优化算法的数据波动最大,稳定性低,导致最短路径和平均路径差距较大;改进五行环算法在稳定性上远优于五行环优化算法,规划出的路径长度也比其他算法短,在简单环境地图中的最短路径和平均路径都能保持在26.307 1 cm,在复杂环境地图中的最短路径和平均路径都能保持在28.4493 cm,在对其进行连接点删除处理之后,甚至能达到26.129 cm和27.602 5 cm的最短路径。
本文设计了栅格环境为30 ×30的简单和复杂地图(障碍物覆盖率为30%),不同算法的路径规划如图6。

图6 不同复杂度地图的30 ×30 机器人路径规划路线
从表2中可知,改进五行环算法在更大的栅格地图中仍然能稳定地规划出一条最优路径,路径长度和拐点数目都明显优于其他算法。在对连接点进行删除处理后,简单地图中的路径长度可以缩短至25.284 6 cm,复杂地图中的路径长度可缩短至43.791 9 cm。
图7为改进的五行环算法的收敛曲线。可以明显看出,在迭代次数为100次时,本文算法在第8代时就已经收敛并保持稳定状态,而其他算法都达不到这么快的收敛速度。

图7 收敛效果
4 结 论
本文结合五行环优化算法和粒子群算法的优点,提出了一种改进的五行环算法,用栅格法对环境进行建模,通过2种不同栅格环境、4 个不同复杂度的地图、5 种不同算法来对机器人的行驶路径进行规划。而且路径上的障碍物数量的不同、路径规划空间的不同,更体现了改进的五行环算法的优势。通过更新机制、突变元子、散开元子和连接点删除等一系列流程后,所得的路径更优、长度更短。仿真结果表明:改进的五行环算法改进使得种群粒子能够跳出局部最优解,提高了算法的性能,也就是说算法的收敛速度和算法的稳定性都得到了大幅提升。

