基于VGG-19 和卡尔曼预处理的WSNs测距方法*

刘超敏，胡玉平

（1.郑州财经学院 信息工程学院，河南 郑州 450000；2.广东财经大学 信息学院，广东 广州 510320）

0 引 言

基于无线传感器网络（wireless sensor networks，WSNs）［1］的测距和定位技术在环境监测等领域得到了广泛的应用。对于测距技术来说，针对无线传感器包含的网络节点间存在的距离进行检测时使用最为普遍的方式为接收信号强度指示（received signal strength indication，RSSI）［2］。从WSNs测距技术的角度出发，其最核心的目的为针对未知节点所对应的信号完成传输过程，进一步转移至锚点以及锚节点组。这些锚节点或远程计算机根据锚节点接收到的无线信号强度，计算未知节点到锚节点组的距离［3，4］。当基于RSSI测距的未知节点进行定位时，距离测量的精度将直接影响节点位置计算的精度［5］。

传统的测距方法包括对数正态阴影模型（log-normal shadowing model，LNSM）、LNSM 校准的自适应神经模糊推理系统以及反向传播（back propagation，BP）神经网络测距模型等［6，7］。基于LNSM 估计是在理想环境的假设基础上进行的。由于最小二乘（least square，LS）法计算未知节点位置时的受测距误差较大，文献［8］提出一种改进花授粉算法的RSSI定位方法易受环境因素影响。文献［9］使用LNSM进行原始估计，基于自适应［10］神经模糊推理系统的智能技术可提高距离估计的准确性，尤其在室内环境中减小了无线多径损伤对信号质量的严重影响。基于BP神经网络的测距模型是将RSSI值用作模型的输入，将距离信息用作模型的输出，并通过训练当前环境中收集的数据来使模型适合当前环境中RSSI 与距离之间的关系［11］。文献［12］提出了一种基于深度卷积神经网络（deep convolutional neural network，DCNN）的测距模型，自动提取在不同地面环境中信号传播的高级语义特征。文献［13］基于BP神经网络模型，引入蚁群优化（ant colony optimizaton，ACO）算法进行优化，寻找最优初始阈值和权值。文献［14］提出了一种基于BP 神经网络的RSSI 测距方法，有效减少了RSSI测距误差。但过多的神经元会增加训练时间，会使网络的泛化能力和预测能力减弱，神经元太少会影响后续值与前体值的关系［15］。虽然BP神经网络测距模型和自适应神经模糊推理系统可以很好地提取当前环境下的信号传播特性，但由于不同环境中信号衰减特性不同［16］。

本文提出了一种基于视觉几何组（visual geometry group，VGG）—19 和卡尔曼预处理的WSNs 测距方法，可以根据图像数据和RSSI数据自动提取不同地面环境的信号传播特性，在不同的地面环境中实现准确的距离估计。

1 VGG-19 网络模型

1.1 VGG—19 的网络拓扑结构

VGG—19网络的拓扑结构如图1所示［17］。其中一段卷积内含有的卷积层数目累计为2～3 个，同时卷积核对应的尺寸为3 ×3，步长为1。

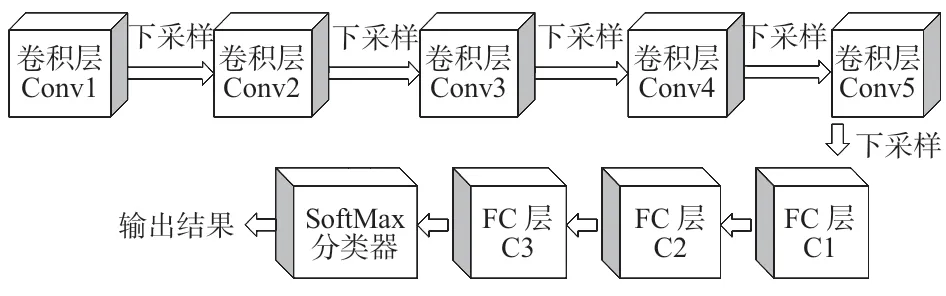
图1 VGG-19 网络的结构

网络中的下采样层采用最大池化（Maxpooling），激活函数采用修正线性单元（rectified linear unit，ReLU）。全连接（fully connected，FC）层的节点数依次是2048，2048，500。除此之外，VGG—19 网络所对应的输入图像尺寸为224 ×224。

1.2 卷积层和激活函数

这里拟定网络内部第l层的第j个特征图表示如下

1.3 下采样层和FC层

VGG—19网络［19］内部的下采样层选择的是Maxpooling，数学形式如下

1.4 损失函数

使用均方误差（mean square error，MSE）损失函数计算损失，L（θ）计算如下

式中 I（i）为输入的图像数据；R（i）为输入的RSSI值；d（i）为测量获得的距离值。通过最小化损失函数进行测距网络的优化。

2 基于VGG-19 的WSNs测距模型

2.1 整体架构

所提模型的整体架构如图2所示。

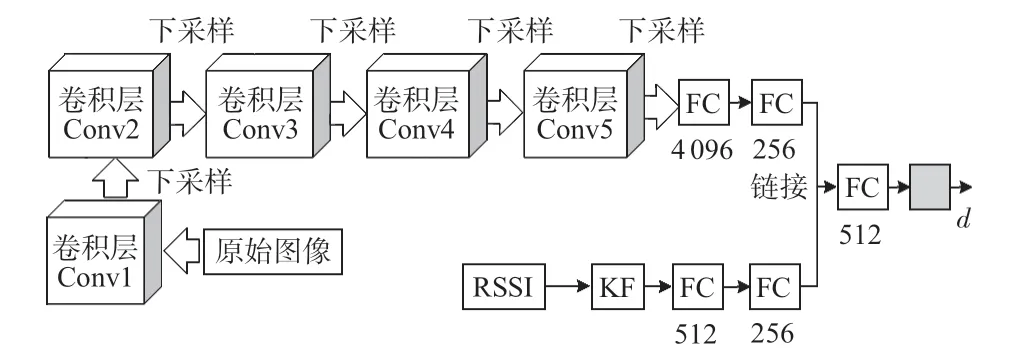
图2 所提模型的整体架构

所提网络模型有2 个输入分支，其中一个分支的输入是来自相机的固定尺寸，224 ×224 的地面图像，该分支包含5 个卷积层，表示为Conv1～Conv5，5 个下采样层（Maxpooling层）和3个FC 层。另一个分支的输入是接收器获得的RSSI值，该分支包含1 个KF器和3 个FC层。然后，将2个分支的输出发送到FC层，基于这些输出值，可以提取信号在不同环境中的传播特性，最终输出的是WSNs 中的距离估计。如果网络中有太多层或隐藏的神经元，则模型的训练时间将增加，但如果层数太少，则模型的训练可能效果不佳。通过对样本大小的分析和实际验证，所提网络模型的参数配置如表1所示，卷积层参数表示为“Conv（感受野大小）-（通道数）”。

表1 网络模型的参数配置

所提网络是一个端到端系统，可以自动提取不同地面环境的信号传播特性。使用地面图像数据和RSSI 数据作为网络的输入，通过网络计算数据后，将获得一个预测结果，即距离估计，它对应于在地面环境中接收到的RSSI值。通过将距离估计值与米尺的真实值进行比较，可以计算出每一层的BP误差，并根据误差调整每一层的参数，直到模型收敛为止。

2.2 基于KF的RSSI数据处理

通过图3能够得出，在完成KF处理的过程后，RSSI数据的波动性［20］出现了明显的下降，其RSSI 值主要在［-60，-58］dBm范围内波动，而原始数据在［-64，-56］dBm范围内波动。由此，表明KF能够有效优化以RSSI 为核心的测距算法所具有的稳定性以及精度。

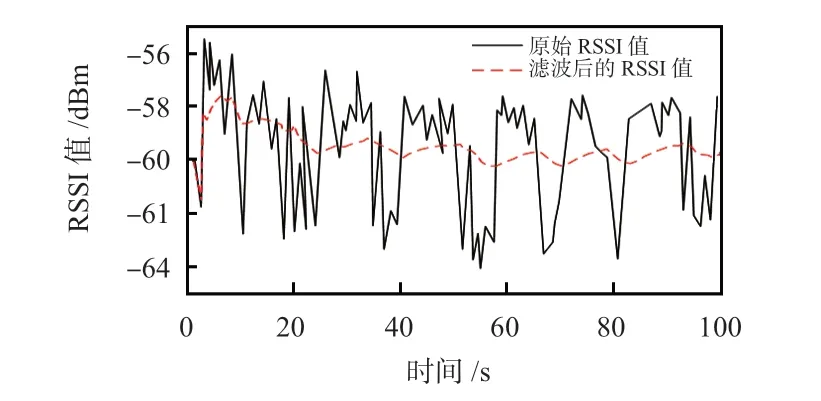
图3 RSSI数据滤波前、后的效果

2.3 测距网络优化

在普通地面环境下，收集了大量的地面图像数据和RSSI测量数据，采用自适应矩估计和BP方法，其中引入了基于平方和平方根的指数加权平均梯度，并利用该值更新参数值［21］。测距网络优化过程的伪代码如下

参数含义：a：步长；β1，β2∈［0，1）：矩估计的指数衰减率；f（θ）：参数θ的随机目标函数；

3 实验结果与分析

实验数据采集装置由RGB摄像头、仪表尺和无线模块组成，由一台计算机完成数据分析，并且装置运行在2.4 GHz微波频带中，RSSI接收器的灵敏度为-97 dBm。动量衰减参数β1为一阶矩，一般为0.9，β2为二阶矩，一般取0.999，ε一般取10-7。

3.1 数据训练

所提模型进行测距需要大量训练数据，包括信号测量数据和图像数据，使用RGB摄像头和无线模块在公共地面环境中收集这些数据，并且使用自适应矩估计梯度降级优化训练VGG—19网络。此外，实验均在带有Titan X GPU的Ubuntu 16.04 系统上进行，网络训练的学习速率为1 ×10-6，一阶矩β1和二阶矩β2的动量衰减参数分别为0.9和0.999。并且使用均方误差作为损失函数来训练和优化模型，直到网络参数θt收敛。

3.2 误差估计分析

实验中，设置了4个场景，分别为理想环境、一般环境、复杂环境和遮挡环境。在所有测试场景中，对所提模型和其他模型计算进行距离估计对比，结果如图4所示。

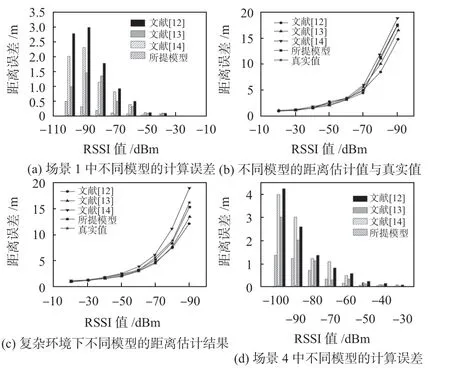
图4 在4 个场景中不同模型距离估计对比

由图4（a）可以看出，在理想环境下，随着RSSI值的增大，距离误差在不断增大，但所提模型的距离估计误差不超过0.5 m，优于其他对比模型。各种模型误差最大不超过3 m，当RSSI值在-50 dBm以内，距离估计误差接近0。由图4（b）可以看出，相比于其他对比方法，一般环境下所提模型的距离估计值与真实值最为接近。尤其是当RSSI 值为-90 dBm 时，文献［12］的估计值与真实值相差大约为3.5 m，而所提模型的估计值仍与真实值十分接近。由图4（c）可以看出，场景变得复杂，相比于一般场景，当RSSI值为-90 dBm，所提模型的误差接近1 m。文献［14］利用BP神经网络实现RSSI测距，以及文献［12］利用DCNN 进行距离估计，两者均使用单一模型，因此对距离的估计效果不佳，得到的估计值与真实值偏差较大，且抵抗外界干扰的能力较弱。而文献［13］在BP 网络的基础上引入ACO 算法进行优化，估计效果有所提升。由图4（d）可以看出，遮挡环境下当RSSI值为-20～-50 dBm时，各模型的距离估计误差均比较小，并且所提模型的估计误差小于0.1 m。当RSSI值衰减到-60 dBm时，误差急剧增加，文献［12］的估计误差超过4 m。由此可见，遮挡这一因素对测距的精度影响很大，但相对而言，由于所提模型在VGG—19网络中引入KF，并且进行训练优化，其得到的距离值误差较小。文献［14］提出的BP神经网络测距模型会产生过拟合现象，因此估计误差较大。同样的，文献［13］在BP神经网络中引入ACO算法，虽有一定的改善，但效果仍不理想。文献［12］的DCNN 模型的估计值与实际测量值存在较大的误差。

3.3 运行效率

由测距时间结果可以看出，所提模型的测距时间为34.92 ms，较文献［12］的28.18 ms，效率有所降低，与文献［14］的35.67 ms基本持平。但文献［12，14］的测距精度不高。而文献［13］综合BP神经网络和ACO算法，测距精度有所提高，但计算效率降低，为46.04 ms。所提模型在VGG—19网络中引入KF，虽然损失了一定的测距效率，但保证了测距精度，因此整体性能最为理想。

4 结 论

本文提出了基于VGG—19和卡尔曼预处理的WSNs测距方法。在搭建的实验平台上，利用数据采集装置进行实验分析，结果表明：在4 种不同环境下，所提模型的距离估计误差均小于其他模型，并且测距时间为34.92 ms，整体性能较为理想。