基于结构化整合的初中数学复习课生态实施探究

倪方友

“双减”政策明确指出，落实立德树人根本任务，着眼建设高质量教育体系，坚持以学定考，进一步提升中考命题质量.《义务教育阶段数学课程标准》（2022版）（以下简称“新课标”）指出，数学课程应以结构化数学知识为载体，在形成与发展“四基”的过程中，让学生形成抽象能力、推理能力、运算能力、几何直观和空间观念.初中数学复习课的生态实施通过向下扎根，向上生长指向数学本质，创新教学方法，优化教学方式，任务驱动，自主生成，可切实提升课堂教学质量和学生学习效率，促进学生发展，形成数学核心素养.

一、结构化整合与生态实施的内涵

1.结构化整合的涵义

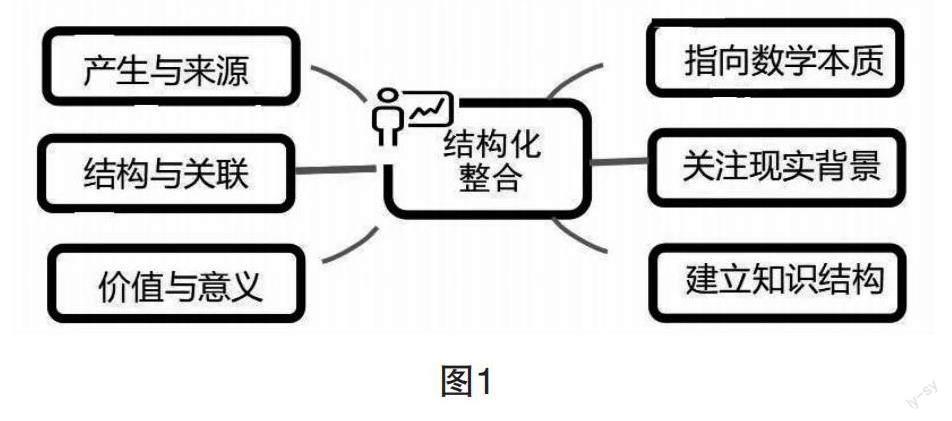
新课标提出，在教学中教师要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系.结构化整合就是按知识的发生及学生的学习发展来进行课程内容结构化设计.基于此，初中数学复习课设计需对知识进行筛选、集约、重组和统合，帮助学生学会用整体的、联系的、发展的眼光看问题，形成科学的思维习惯，发展数学核心素养（如图1）.

2.生态实施的内涵

生态实施是指课堂上协调教师、学生、知识、教育技术及环境的和谐统一和平衡，聚焦核心素养，在任务驱动下，学生通过独立思考、自主探索、动手实践、合作交流，让学习自然而然地发生，让学生获得发展，形成能力和素养.生态实施有五个策略：植根立本策略、任务驱动策略、合作学习策略、教学纯净策略、和谐共生策略（如图2）.

二、初中数学复习课的生态实施范式

基于结构化整合的初中数学复习课的生态实施的理念，构建复习课的基本范式结构（如图3），践行一个目标、两大杠杆、三个主体、四个原理、五大策略、六个设计和“545+”生态评价，以“向下扎根——知识构建与模型呈现，向上生长——典型题例分析与方法挖掘，深耕厚植——课堂过关诊断和方法技巧小结”为实施路径，让学生达成知识结构整联、基本技能熟练、典型题型练全、通性通法理解、问题解决创新和能力素养集成.

三、初中数学复习课生态实施教学实践

（一）内容结构化整合

1.知识内容解析

“二次函数的图象和性质”是学习完一次函数、二次函数概念后的进一步探索，是对二次函数的深度理解，是对函数的图象和性质研究的路径和方法的进一步应用和巩固.本节知识是初中数学数与代数领域研究中，较复杂的数形结合思想的研究，也是对方程、不等式、一次函数的综合运用，是培养学生模型观念的最好载体.本节知识的显性知识点和隐性关联点如图4：

2.层次要求厘清

该节知识内容按课程标准要求的两个维度：第一，知识技能要求.二次函数的概念和解析式要求达到理解的层次；二次函数的图象和性质要求达到掌握的层次。第二，过程性要求.二次函数的图象和性质要求学生达到体验的层次.具体要求见表1所示：

3.素养方法挖掘

本节知识学生需要的核心素养有：抽象能力，几何直观，模型观念和应用意识；数学思想有类比思想，数形结合思想，整体思想等.

4.教学目标设计

掌握二次函数的图象及性质的本质特征；根据二次函数的特征和性质解答综合题型，进一步熟悉研究二次函数的方法和路径；通过本次复习，让学生进行知识网络的构建，培养学生积极思考、解决问题的学习品质，知道事物之间变化的关联性.

（二）教学环节

1.知识网络构建

任务一：二次函数的图象和性质

设计意图：学生通过独立完成表2的填写，进一步巩固知识，熟悉二次函数的图象和性质.

2.方法模型呈现

任务二：你学过的二次函数有哪些形式？（师生共同回忆，教师构建网络图如图5）

设计意图：让学生理解二次函数的不同形式及特点，以及它们之间的相互关系.

3.典型例题分析

任务三：如图6，根据二次函数y=ax2+bx+c（a≠0）的图象，你能得到哪些结论？

如图7，如果我们添加以下条件：对称轴为直线x=1，與y轴交于点B（0，2），点A（1，m）在抛物线上.请你写出至少三个正确的结论____________________.

设计意图：学生根据图形的特征回答，初步感知二次函数的图象和性质，培养数形结合思想，知道给出的条件越明确，函数的特征越精确.

例题分析：已知抛物线y=-x2+bx+c经过点（0，3），当x<1时，y随x的增大而增大，当x>1时，y随x的增大而减小.

教师提问：你能得到哪些结论？请在图6中画出这个二次函数的图象.

教师追问：根据图象回答下列问题：

（1）当x为何值时，y>0？当x为何值时，y<0？

（2）点P1（-3，y1），P2（2，y2），P3（3，y3）在抛物线上，判断y1，y2，y3的大小，你是如何判断的？

（3）直线l交抛物线于点A（-2，m），B（n，-12），n为正数.若点M在抛物线上且在直线l上方（不与点A，B重合），分别求出点M横坐标与纵坐标的取值范围.

设计意图：本题设置成结论开放性题型，先由教师出示题干，让学生根据条件得结论，并让学生作出图象，培养学生动手操作能力；然后根据图象解决问题，进一步巩固二次函数的图象和性质，深刻体会数形结合思想的作用，培养学生几何直观意识.

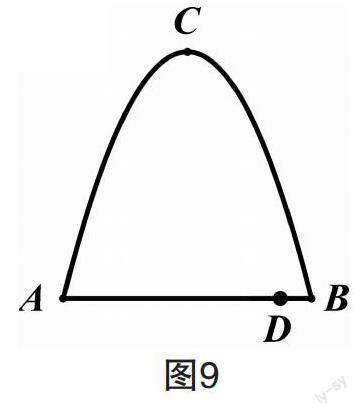
任务四：如图9，从A点向外喷水，水柱为抛物线，落地点B离A点4米，水柱的最高点C离地面4米，与A点的水平距离为2米.在离A点3.5米的D处竖立高为1.6米的雕塑DE，顶部E是否会碰到水柱？

设计意图：本题是一道方法开放试题，先由学生合作探究完成，再分别汇报.解答中，学生建立的坐标系不同，得到的解析式是不同的，但是无论怎样建立平面直角坐标系，最终结果是一样的.通过小组合作探究，教师可以培养学生合作能力，探究能力，表达能力.

4.课堂过关诊断

练习1：★如图10，是二次函数y=ax2+bx+c（a≠0）图象的一部分，且过点A（-3，0），二次函数图象的对称轴是直线x=-1，下列结论正确的是（ ）

A.b2<4ac    B.ac>0

C.2a+b=0    D.a+b+c=0

设计意图：练习1是一星级题，是一道已知二次函数的图象，需要学生得出它的性质的题目。学生容易入手，有获得感.

练习2：已知抛物线y=ax2-2x+1（a≠0）与x轴只有一个公共点.

（1）★求a的值；

（2）★★若点M（x1，y1），N（x2，y2）都在此抛物线上，且-1

（3）★★★设直线y=4与抛物线y=ax2-2x+1交于點A，B，与抛物线y=4（x-1）2交于点C，D，求线段AB与线段CD的长度之比.

设计意图：练习2属于二次函数的图象和性质较综合性的解答题，分成三个小题，设计有梯度和层次性.第（1）问学生比较容易解决属于一星级问题，第（2）问有一定的难度属于二星级题，第（3）问挑战自我难度进一步提升，对有探究兴趣和学有余力的学生“量身定制”，属于三星级题，这种分层设计从不同的角度和层次考查了学生对知识技能掌握情况.

四、初中数学复习课生态实施的教学思考

1.评价指向

初中学业水平考试评价指向是“坚持素养立意，凸显育人导向”“创设合情境，设置合理问题”，注重“四基”“四能”的考查.坚持以学定考，以评促学，试题源于教材，又联系学生生活实际，切实减轻学生负担.在中考复习阶段，教师努力去构建结构化整合的复习课，生态实施，根植核心素养，让“双减”落地到课堂，切实提升教育质量.

2.创新设计

创新点1：教学流程的纯净与优化.复习课设计了五个流程：知识网络构建，方法模型呈现，典型题例分析，课堂过关诊测和方法技巧小结.

创新点2：直击数学本质.二次函数的图象和性质主要是从开口方向、对称轴、顶点坐标、极值和增减性等五方面进行探索.本节课牢牢抓住了二次函数的图象和性质的本质特征，从三个方面入手：“试一试”设计是知道二次函数的图象说出性质特征；“例题”设计是知道二次函数的条件特征，准确得到图象，再通过图象回答问题；“问题解决”的设计是建立二次函数模型，解决实际问题，培养学生应用意识.

创新点3：典型题例以问题串和开放式教学设计，培养学生思维能力.从一个常见的二次函数的图象入手，叫学生快速得到相应的性质；然后再通过添加条件，可以更加精准刻画这个二次函数的性质特征；例题设计采取了结论开放设计，问题解决采取了条件开放设计，让学生通过独立思考，交流合作，实践操作解决问题.

◇责任编辑 邱 艳◇