考虑道路修复的应急物资选址与配送双目标优化研究
殷允强, 罗琴凤, 陈 旭, 王杜娟, 徐新蕊
(1.电子科技大学 经济与管理学院,四川 成都 611731; 2.四川大学 商学院,四川 成都 610065)
1 引言
随着地球生态环境恶化,世界各地频繁突发自然灾害,给人类生命安全和社会发展带来了巨大威胁。党和国家对于灾后救援工作给予高度重视,党的十九届四中全会提出了“优化我国应急管理能力体系建设,提高防灾减灾救灾能力”的努力方向。其中物流工作是决定救援行动成功与否的关键[1],而救援物资供应的有效性在很大程度上取决于灾区道路网络的状况。尤其在极端自然灾害后,道路、桥梁、隧道等交通基础设施中断,需要及时修复受损道路以保障应急物资配送效率。因此,有必要对考虑道路修复的应急物流集成优化问题展开深入研究[2],提高灾后应急救援的社会效力和经济效率。
在考虑道路修复的应急物流集成优化研究方面,按照维修车辆的数量,可分为单维修车辆问题和多维修车辆问题。在单维修车辆问题上,Maya-Duque等[3],Moreno等[4,5]以最小化需求节点可达时间的加权和为目标,研究了维修车辆调度及救援车辆路径问题。Shin等[6]对Maya-Duque等的模型进行拓展,增加了救援车辆调度决策,以最小化需求节点最晚可达时间为目标,并设计蚁群算法进行求解。Kim等[7]考虑了修复工作的黄金时期,若在黄金时期后仍未对灾区进行访问将给予较高惩罚,还考虑了修复工作的完成时间最小化,同样设计蚁群算法进行求解。可以发现,无法进入受灾地区会导致疏散、救援和医疗援助等活动延误,因此及时、有效地修复受损的道路网络对应急物流至关重要。
在多维修车辆问题中,对于某维修车辆负责修复的受损节点,其他车辆必须等待该受损节点恢复才可穿越路网。因此,除考虑救援车辆和维修车辆的配合,各维修车辆也需相互协同工作。Xu和Song[8]研究了最小化救援物资到达时间的灾后多维修车辆调度与救援车辆路径优化问题。李双琳和郑斌[9]构建了综合考虑震后路网抢修排程与应急物资配送的动态双层规划模型,并设计稳态混合遗传算法进行求解。Li等[10]认为灾后道路修复工作的开展依赖于有效的后勤保障,将维修车辆调度与后勤保障调度进行集成优化,并设计两阶段启发式算法进行求解。张梦玲等[11]为实现精准的物资配送与道路修复决策,基于手机定位数据构建混合整数线性规划模型,并设计嵌套遗传算法和蚁群算法进行求解。Moreno等[12]认为现有研究忽略了维修车队的异质性,探究了异构多车的道路修复和救援路径规划问题。上述研究表明,多维修车辆和多救援车辆协同工作更加符合实际救灾场景,能有效提升灾后响应阶段的应急救援效率。
综上可知,目前路网维修和应急物流优化已有一定研究成果,但鲜有研究综合考虑灾后道路修复、应急物资选址与配送的多目标集成优化问题。而救灾仓库的位置对后续救援调配工作的效力和效率具有重大影响,需要在灾后应急管理决策中综合考虑救灾仓库选址。并且由于上述组合优化问题的复杂性和灾后响应阶段的时间紧迫性,也难以设计有效算法进行精确求解。此外,灾后应急物流的首要任务是减轻灾民痛苦,必须着重关注缓解灾民心理创伤,避免发生重大社会问题。除了考虑救援经济成本,救援行动对灾民心理的影响是不可忽略的社会成本,也应被考虑为一项重要的决策目标[13]。
基于此,本文针对地震等自然灾害的实际救援需求,(1)综合考虑灾民无法及时获得救援物资的痛苦感知和实际救援经济支出,并将之量化为匮乏成本和救援成本,构建道路修复、应急物资选址与配送的双目标集成优化模型。(2)设计基于密度峰值聚类的非支配排序遗传算法II进行求解,并引入初始解生成策略、基于聚类轮廓系数的不动点策略以及变邻域局部搜索策略对算法进行改进。(3)利用汶川地震案例和随机算例,验证上述模型和算法的有效性,并提炼管理启示。
2 问题描述与模型构建
2.1 问题描述
考虑道路修复的应急物资选址与配送集成优化问题定义在无向图G=(V=Vd∪Vr,A)上。其中V为节点集合,A为弧集,Vd⊂V为需求节点集合,Vr⊂V为受损节点集合,Vs⊂Vd为候选救灾仓库集合,Ks为仓库s∈Vs处的救援车辆集合。记Vs=(VVs)∪{s},Vs′=(VVs)∪{s′},其中s′为节点s的复制节点。需求节点i∈Vd的救援物资需求量为di,受损节点i∈Vr的维修时间为ri和维修成本为ui,弧(i,j)、弧(l,m)∈A的旅行时间为tij和tlm。拟开设救灾仓库的总数量为D_num,仓库s∈Vs的开设成本为Fs,启用一辆救援车的固定成本为R,救援车辆和维修车辆的单位时间旅行成本为c。M为充分大的数。

相关假设如下。(1)需求节点的数量、位置、需求量已知。(2)每个受损节点和需求节点都仅由一辆车服务一次,且各需求节点的需求被完全供应。(3)每个候选仓库配置有限个容量为C的同规格救援车辆,以及数量充足的同规格维修车辆。(4)每个救援车辆可服务多个需求节点,每个维修车辆最多只修复一个受损节点。(5)所有被指派车辆均在零时刻从仓库出发,结束任务后返回原仓库。(6)不考虑维修车辆返回路径。
为有效度量救援效力,本文利用救援物资匮乏时长来描绘灾民无法获得物资的痛苦感知,定义匮乏成本函数为Γ(t)=a(eb×t-1),其中a、b均为常数[13],t为救援车辆达到需求节点的时间。
2.2 模型构建
基于以上参数,构建如下数学规划模型
(1)

(2)
(30)

3 算法设计
上述模型为双目标非线性规划模型,难以设计有效的精确算法进行求解。为了在灾后响应阶段快速求解此类复杂的集成优化问题,本文设计一种基于密度峰值聚类的非支配排序遗传算法II,快速求得近似帕累托最优解集。该算法利用密度峰值聚类(density peaks clustering,DPC)算法快速选定救灾仓库的位置,采用Floyd算法决策受损道路修复方案,并获得各受损节点的最早修复完成时间。然后,利用非支配排序遗传算法II(NSGA-II)确定应急物资配送方案及需修复的受损节点。最后,设计初始解生成策略、基于聚类轮廓系数的不动点策略以及变邻域局部搜索策略对上述算法进行改进,记为CGAVNS算法。整体算法流程如图1所示。
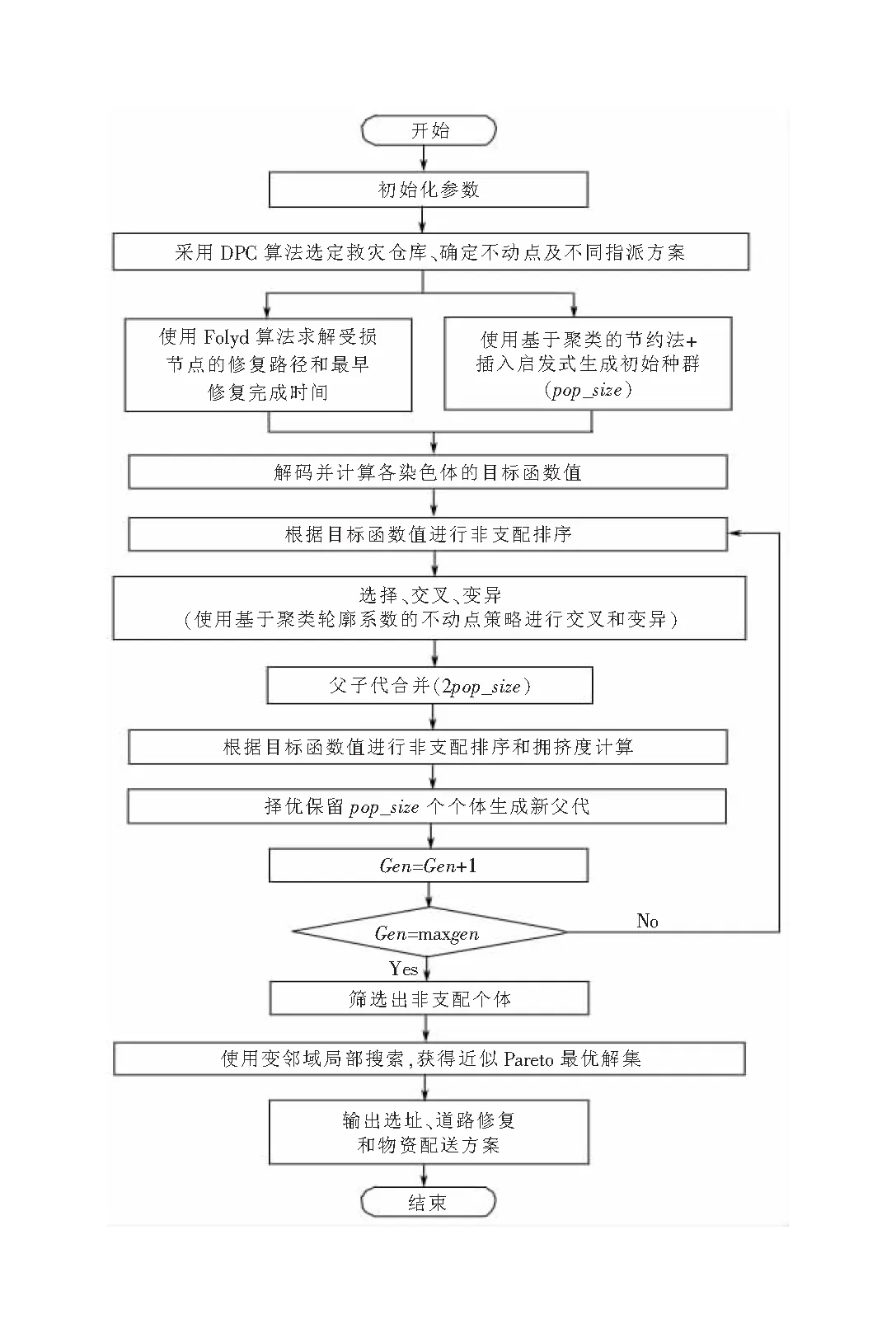
图1 CGAVNS算法流程图
3.1 救灾仓库选址算法设计
本文首先基于DPC算法确定若干个聚类中心和相应群簇,选定聚类中心作为救灾仓库,其群簇作为相应客户群,基于此生成救灾仓库和各需求节点的初始指派方案。然后利用聚类轮廓系数,衡量各群簇内的紧密程度以及各群簇间的离散程度,以此生成其他指派方案,用于后续初始解生成。关键算法步骤如下:
(1)确定救灾仓库:计算局部密度ρi和相对距离δi,记γi=ρiδi,将γi降序排列,选择前D_num个需求节点作为聚类中心s,即救灾仓库。
(31)
(32)
其中dij为节点i和j之间的最短距离,dc为截断距离,qi表示按ρi降序排列的节点序列,即ρq1≥ρq2≥…≥ρqN。
(2)非聚类中心指派:确定局部密度比i大的节点中与i距离最近的节点编号ni。记聚类中心的类别标签为其本身,非聚类中心i的类别标签与ni一致。据此,将非聚类中心i(其他需求节点)指派给救灾仓库进行服务。
(33)
(3)确定不动点并生成其他指派方案:计算各非聚类中心的轮廓系数Si和最近簇,将Si升序排列,选择后1-α比例的节点存入不动点集合constant。再将[0,α]比例的非不动点重新指派到其最近簇中,生成不同指派方案。
(34)
其中ai为i与同簇其他节点的平均距离,bi=biJ=min{bi1,bi2,…,biK}为i与其他簇中所有节点平均距离的最小值,J为节点i的最近簇。
3.2 受损道路修复算法设计
本文采用Floyd算法的思想,求解到各受损节点最快的修复路径以及相应修复完成时间。由于考虑了多维修车辆协同工作,当某维修车辆的修复路径经过其他受损路段,若该受损路段已被其他维修车辆修复,则车辆可直接行驶;若当该维修车辆到达时上述路段尚未完全修复,则车辆需等待至该路段修复后才能通行。因此,在使用Floyd算法时需要单独计算并更新各受损节点的最早修复完成时间,且在利用路径矩阵进行路径扩展时,必须检查路径中是否含有受损节点。
3.3 应急物资配送算法设计
使用改进的NSGA-II算法决策应急物资配送方案,相关操作和步骤如下:
(1)染色体编码
两段式染色体编码方式能够消除部分冗余解,提高算法的搜索效率[14]。其中第一部分为需求节点的排列编码,第二部分为各仓库的各救援车辆对应访问的需求节点数。例如,现有15个需求节点,2个救灾仓库(记为仓库1和2),每个救灾仓库2辆救援车,则根据上述编码规则,可得到图2的一条染色体。图2表示仓库1的救援车辆1供应6个需求节点,配送顺序为3-8-13-7-1-10,仓库1的救援车辆2不启用;仓库2的救援车辆1供应4个需求节点,配送顺序为2-9-15-11,仓库2的救援车辆2供应5个需求节点,配送顺序为4-6-12-14-5。
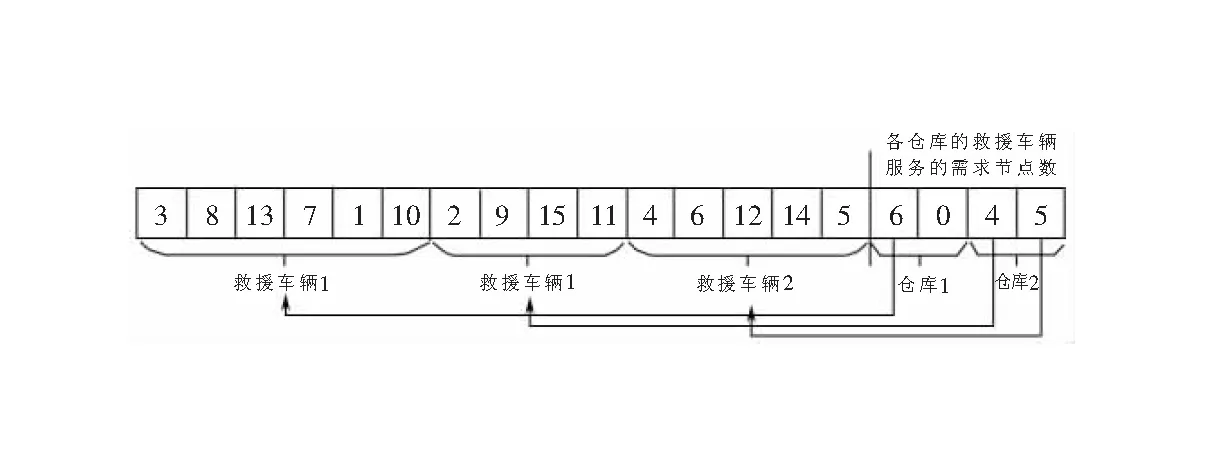
图2 染色体编码示意图
(2)染色体解码
根据染色体的编码思路,先将染色体按照车辆拆分成配送顺序s-s′(k),然后检查两相邻需求节点(i和i+1)的配送路径ODi是否经过受损节点。若经过受损节点,救援车辆可能会发生等待,则需将受损节点的最早修复完成时间用于救援车辆到达时间的计算。对应各路径累积计算匮乏成本和救援成本,进而解码得到染色体的适应度。
(3)初始解生成
使用基于聚类的节约法生成一部分高质量的初始解。以各聚类中心s为节约法的基点,在其群簇内,基于节约值,利用贪婪策略将各需求节点插入救援车辆路径中,形成各仓库客户群的较优配送路径,最终初始解为所有客户群对应的配送路径组合。基于3.1节的多种指派方案,生成不同的初始解。
为保证初始解多样性,使用插入启发式生成另一部分初始解。核心步骤为:通过准则φ1找到需求节点j的最佳可行插入位置,通过准则φ2选择最佳需求节点j*,再将j*插入到路径中的最佳可行插入位置。(35)式表示插入节点j后服务需求节点m和l总旅行时间的增加量,其中Tlm为两节点之间的总旅行时间;(36)式表示插入节点j后路径总匮乏成本的增加量,其中route为原路径,route′为插入节点j后的路径。
(35)
(36)
(4)遗传算子
采用轮盘赌策略进行染色体选择,使用自适应选择psi、交叉pci概率进行遗传进化,其中ranki为个体i在种群pops中非支配排序后的等级,pops={1,2,…,pop_size},pc为固定交叉概率。
(37)
(38)
参考特殊的两段式染色体交叉算子[15]进行交叉操作,并利用聚类获得的不动点集合constant对交叉算子进行改进,后续算法搜索过程中不动点与仓库的指派关系不变,从而提高搜索效率。给定一对待交叉的染色体c1和c2,假设以染色体c1为基础,生成子染色体child1。首先从c1的各路径中随机选择一个基因片段(子路)保留下来,然后根据c2第一部分的基因顺序对上述未保留基因进行排序,将未保留基因Q排序为Q′。接着,根据constant确定Q′中的不动点并按照仓库拆分。然后,基于车辆容量约束和各仓库不动点限制,产生可行随机数,按照随机数将Q′中的基因新添到c1各路径中,最终形成子染色体child1。类似地,再以染色体c2为基础,可生成另一条子染色体。
设计4种变异算子:①Inter_exchange:随机选择两条配送路径,若属于同一仓库,则在容量约束下,再各自随机选择1个需求节点进行交换;否则,只能选择非不动点进行交换。②Inter_relocation:随机选择两条配送路径,若属于同一仓库,则从需求节点数较多的路径中随机删除1个节点,在容量约束下,再随机插入另一条路径;否则,只能选择非不动点进行删除插入。③Intra_exchange:随机选择同一配送路径中的2个需求节点进行交换。④Intra_relocation:随机删除一条配送路径中的1个需求节点,再随机插入该路径的其他位置。
(5)变邻域局部搜索
采用变异阶段的4种算子构造邻域动作集Nl=(N1,N2,N3,N4),对最后一代的非支配个体进行变邻域局部搜索,避免算法陷入局部最优。主要核心思想为:若在邻域搜索次数内找不到比当前解更优的解,则跳到下一个邻域继续搜索;若找到了更优解,则以此为最好解重新进行变邻域搜索。
4 数值实验
以2008年汶川地震案例和随机算例进行数值实验,验证本文模型和算法的有效性。使用软件Python 3.8进行编程,运行在AMD Ryzen 7 4800U@1.80Ghz的CPU,16.0GB内存的笔记本电脑上。
4.1 案例背景
依据汶川地震灾情报告,共设38个物资需求节点(0-37),16个道路受损节点(38-53),需开设3个救灾仓库,各仓库备有6辆救援车,车辆容量为1800,单个仓库的开设成本为30000元,旅行成本为8元/分钟,受损节点的维修成本设为维修时间的100倍。灾区路网如图3所示,路径上的数值为旅行时间(分钟),括号中的数值为需求节点的需求量(个)或受损节点的维修时间(分钟)。匮乏成本函数中相关系数为:a=1.5,b=0.12[13]。算法相关参数设置如下:种群规模pop_size=60,进化代数maxgen=60,交叉概率pc=0.9,变异概率为pm=0.1,邻域搜索次数S=15,邻域搜索循环次数max_N=20,截断比例ε=0.02,不动点比例α=0.6。

图3 汶川地震灾区路网图
4.2 案例求解
基于上述案例背景,以Pareto解集中匮乏成本和救援成本中位数对应的解为例,展示最终救援决策方案。CGAVNS算法求解得到的救灾仓库为节点12、节点23和节点32,分别记为仓库1、2、3,启用的救援车辆数分别为6、4、3。救援车辆配送路径如表1所示,共需修复8个受损节点,维修车辆修复路径如表2所示。整体决策方案的匮乏成本为20819元,救援成本为515712元,其中仓库建设成本为90000元,救援车辆启用成本为13000元,道路修复成本为384000元,车辆旅行成本为28712元。

表1 救援车辆配送路径及物资到达时间

表2 修复路径及修复完成时间
4.3 修复策略验证
本节取受损节点完全修复和部分修复时目标值中位数所对应救援结果进行比较分析。参考文献[16]和实际调研,按照各节点平均连接弧数γ取3、4、5(分别表示乡村、混合和城市路网),路网受损率ϑ取10%、30%、50%,随机生成了100个需求节点的9种随机算例。

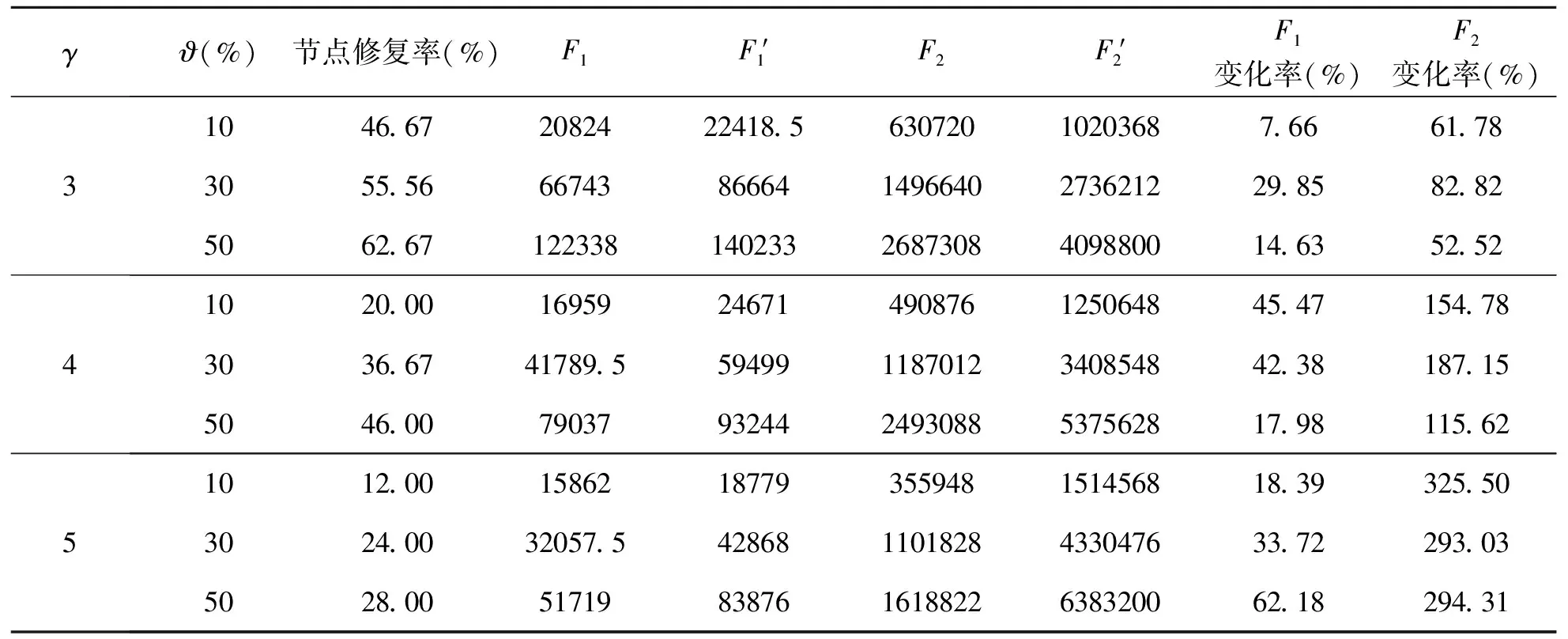
表3 受损节点部分修复和完全修复结果对比
基于上述数值分析,当发生地震、洪水、海啸等极端自然灾害后,可总结以下三点管理启示:(1)灾区路网越稀疏越应重视路网修复,农村地区应配备更多的道路修复人员和相关设备。(2)灾情越严重越应重视灾区路网修复,从而及时恢复灾区路网的连通性和可达性。(3)相较于受损路段完全修复,只修复部分关键受损路段效益更高,尤其在城市路网中。
4.4 算法有效性分析
本节将不进行改进的基础算法CNSGA-II与只添加初始解生成策略的算法CNSGA-II+IS、只添加不动点策略的算法CNSGA-II+CN、只添加变邻域局部搜索策略的算法CNSGA-II+VNS以及添加所有改进策略的算法CGAVNS的求解结果进行比较。选择30%路网受损率的随机算例100-3-30、100-4-30、100-5-30,从超体积(HV)和运行时间(T)两个性能指标上,验证算法改进策略的有效性。表4给出了各算法的HV值和T值,以及相较于基础算法CNSGA-II的变化率(记为CR)。

表4 CNSGA-II与CNSGA-II+IS、CNSGA-II+CN、CNSGA-II+VNS、CGAVN结果比较
总体来看,相较于基础算法CNSGA-II,添加各策略后的算法均有明显的改进。这是由于本文算例参考实际路网,均为稀疏图,算法在全局搜索过程中局部最优非常严重且难以跳出。具体来看,(1)初始解生成策略在算法求解时间上优化效果最好,相较于基础算法,CNSGA-II+IS求解时间平均降低约82%。这说明本文的初始解策略可明显加快算法的寻优速度,从而使算法在较少的迭代数下收敛。但CNSGA-II+IS算法仍无法避免陷入局部最优,CGAVNS以增加约9%的求解时间,换取超体积值提升72%。(2)变邻域局部搜索策略在超体积指标上优化效果最好,相较于基础算法,CNSGA-II+VNS超体积值平均提升约70%。这说明本文的局部搜索策略可有效解决局部最优问题,明显提高解的质量。但CNSGA-II+VNS相较于CGAVNS,需花费更多时间在全局寻优上,CGAVNS的超体积值与之差异不大,但求解速度提升约13%。(3)基于聚类轮廓系数的不动点策略在算法运行效率上有一定程度的优化,但在HV指标上表现较弱。可能原因是:不动点策略在算法搜索过程中,限制轮廓系数大的需求节点与仓库的指派关系不变,从而避免无效搜索、加快寻优速度,但同时也会因限制搜索从而遗漏一些高质量解。
5 结论与启示
本文针对极端自然灾害的实际救援需求,对道路修复、应急物资选址与配送集成优化问题展开研究。以匮乏成本和救援成本最小化为目标,构建考虑道路修复的应急物资选址与配送双目标优化模型,设计基于密度峰值聚类的非支配排序遗传算法II进行求解,并添加初始解生成策略、基于聚类轮廓系数的不动点策略以及变邻域局部搜索策略进一步改进算法性能。最后,利用数值实验验证模型和算法的有效性。结果表明:(1)本文模型和算法具备较好的应用性,可以帮助决策者在社会成本和经济成本的权衡下做出科学的救灾战略规划。(2)灾情越严重、灾区路网越稀疏,越应重视灾后道路修复,且在应急响应阶段只需修复关键受损路段便可高效支撑救援任务,从而为实际救援节约人力物力,实现救援效益最大化。(3)三种算法改进策略均有明显优化效果,设计的CGAVNS算法具备较好的综合求解性能,能够在灾后快速生成较优的救援方案,保障救灾工作的效力和效率。
未来研究工作可考虑灾害的多维不确定性和动态性,研究动态多周期的道路修复和资源调配问题,并利用大数据技术实时获取灾民需求、定位等数据,探究实际灾害情景的表征手段和建模方法。另外,实际救援中还会设置后勤工作站以作维修资源供给,如何进行异构维修车辆协同调度及工作站选址分配也有待进一步探究。

