双半球胶囊内窥镜流体环境姿态稳定性研究

邢立君,张永顺,孙立峰,董 海

(大连理工大学高性能精密制造全国重点实验室,辽宁 大连 116024)

0 引言

近年来,胶囊内窥镜已成为胃肠道疾病的主要检查方法。与侵入式内窥镜相比,胶囊内窥镜已经成为小肠内临床检测的唯一手段,减轻了患者的痛苦,因此,胶囊内窥镜已成为国内研究热点[1]。目前,AnHon(中国安翰)、OMOM(中国金山)、EndoCapsule(日本OLYMPUS)以及M2A(以色列GIVEN IMAGING)等公司[2-3]推出了多种胶囊内窥镜产品。其中,M2A胶囊内窥镜的运动依赖胃肠道自然蠕动,不能主动操控,仅适用于肠道检查。其余型号胶囊内窥镜在此基础上改进,由外部永磁体与胶囊内部永磁体间相互作用产生驱动力而主动行走,适用于宽裕胃部环境检查,可对病灶反复观查。目前,胶囊内窥镜的发展趋势是集诊断、施药和活检等功能一体化[4-5],而实现精准施药、活检功能需保证胶囊姿态和位置调整准确。然而,在结构方面,现有胶囊内窥镜滚动行走和姿态调整耦合,姿态调整难度大,位置控制精度差[6]。在驱动磁场方面,现有主动胶囊主要采用外部永磁体产生的磁场属于梯度磁场驱动,对距离敏感,对控制外部永磁体的机械臂系统要求严格,同时,胶囊姿态调整困难,不利于活检、施药功能的实施。因此,研发姿态、位置控制准确的新式胶囊内窥镜非常重要。

本文提出了一种基于电磁线圈驱动的双半球胶囊内窥镜机器人[7]。与现有胶囊内窥镜系统相比,启发于双自旋卫星,提出了一种主被动半球结构胶囊机器人,双半球胶囊内窥镜既可整球行走,又可半球悬浮调姿,实现了姿态调整和主动行走的主动分离。双半球胶囊内窥镜具备很大的诊疗一体化发展潜力,与体外永磁体驱动相比,采用了空间万向旋转磁场电磁驱动,仅需改变输入电流大小即可灵活、准确地实现均匀旋转磁场大小与方位的控制。

本文建立了流体环境下双半球胶囊内窥镜滚动行走模态动力学模型,对胶囊滚动姿态稳定性进行了仿真分析,给出控制参数的选取方式,并设计胶囊内窥镜系统进行实验验证。

1 双半球胶囊内窥镜系统

双半球胶囊内窥镜系统主要包括电磁线圈及其控制系统以及胶囊内窥镜。

三轴亥姆霍兹电磁线圈如图1所示,在3组线圈中通入不同电流大小、方向和相位的交变电流,即可在线圈中央生成磁场强度、方向和旋转频率不同的匀强空间万向旋转磁场。磁场控制灵活,反应灵敏,可为胶囊内窥镜提供足够的动力。

图1 电磁线圈装置

双半球胶囊内窥镜如图2所示,其主要由上下2个半球构成。上半球中集成了图像采集模块、LED照明模块以及永磁体磁环,上半球球壳与永磁体固连,上半球可随之旋转,称为主动半球。下半球集成了电池以及无线传输模块,由轴承与主动半球连接,可实现上半球球壳旋转而下半球及摄像、照明模块不动,因此下半球称为被动半球。这样的结构不仅利于胶囊的姿态调整,还保证了姿态调整过程采集的图像不转动,利于高效诊断。

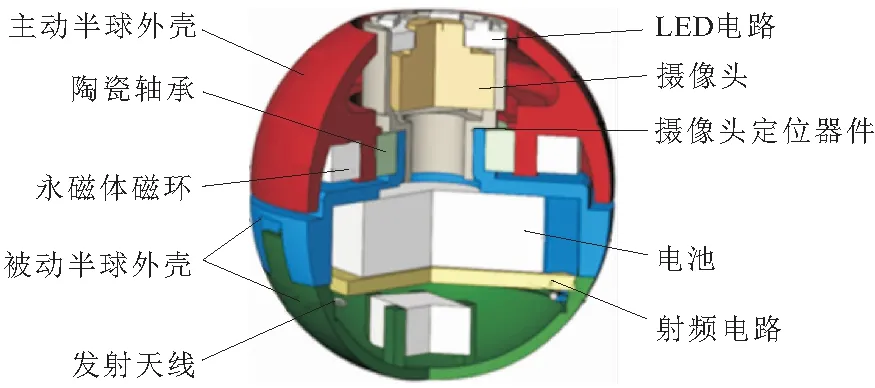
图2 双半球胶囊内窥镜结构

双半球胶囊内窥镜系统的工作原理是控制电磁线圈产生旋转磁场,当控制磁场使得胶囊主动半球不与胃肠道接触后,主动半球悬离,被动半球在胃肠道摩擦力作用下停止转动,胶囊整体处于定点调姿模态[7]。当旋转磁场与胃部垂直时,随动效应驱动胶囊主动半球与胃肠道接触,在摩擦力或流体力的作用下主动行走。

2 胶囊滚动动力学建模

在饮用大量液体后,胃部褶皱平缓,因此可将胶囊在胃部表面运动时视为球-平面系统。流体环境下胶囊在胃部表面运动可视为弹性流体动力润滑[8],即胶囊在滚动时不与胃肠道接触,而是由流体润滑膜间隔,此时胶囊不再做纯滚动,而是以连滚带滑的形式做滑滚运动。

2.1 建立坐标系

建立如图3所示的坐标系描述胶囊姿态调整时的滑滚运动状态。图3中,R为胶囊半径;B、ω分别为磁矢量及其转速;P为胶囊与流体润滑膜接触点;P′为胃肠道与流体润滑膜接触点;δ为油膜厚度,是两接触点的距离。

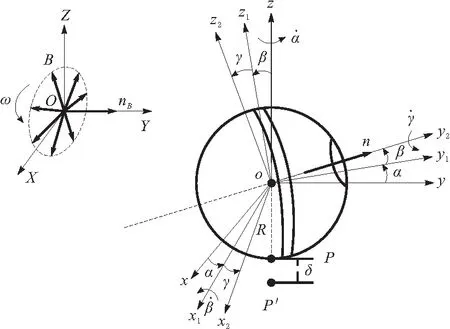
图3 胶囊滑滚运动状态

a.OXYZ为固定坐标系,Y为磁场旋转平面法线nB方向。

b.oxyz为平动坐标系,原点在球心o处。

c.ox1y2z1为描述胶囊倾斜姿态的赖柴坐标系,是由坐标系oxyz绕z轴旋转α角得到中间坐标系ox1y1z,再绕x1轴旋转β角后得到。机器人轴线n方向沿y轴。

d.ox2y2z2为与胶囊固连的本体坐标系,由坐标系ox1y2z1绕y1轴旋转γ角后得到。

胶囊任意时刻的位置和姿态分别由球心o的位置信息x、y、z及广义欧拉角α、β、γ确定。

胶囊的速度由转动速度以及滑移速度构成,在oxyz坐标系中可描述为:

(1)

U=[uxuyuz]T

(2)

2.2 力和力矩计算

根据耦合磁矩公式T=m×B,耦合磁矩TB在平动坐标系oxyz内表示为

(3)

胶囊在流体环境下胃部表面动力学建模的难点,是胶囊在平面附近运动时所受到的流体力和力矩的计算。由于机器人半径小、运动速度低及流体粘度较大,因此,流体环境可视为低雷诺数Stokes流体。低雷诺数流体运动的惯性效应通常可以忽略不计,因此,作用在胶囊上的流体力及力矩与胶囊的速度和转速直接相关[9],可表示为

(4)

F、τ分别为胶囊所受到流体力和力矩;A为系数矩阵。

Caldag等[10]进行了系列化模拟实验研究,研究结果表明系数矩阵A中大部分参数要远小于对角线参数,因此可以设定为0,胶囊所受到的流体力和力矩可表示为

(5)

式(5)中的系数均可由球位于平面附近单一运动的相关流体力和力矩的计算方式得到[10],各系数表达式为

(6)

μ为流体动力粘度;R为胶囊半径;δ为油膜厚度。

可见,油膜厚度影响胶囊所受流体力和力矩。经计算,胶囊在胃部表面运动时处于刚性-等粘度润滑状态,油膜厚度计算式[11]为

(7)

hf为膜厚参数;U0为卷吸速度;W为载荷。各计算式分别为

(8)

k为椭圆率,对于双半球胶囊可取1;ρ油为流体的密度;g为重力加速度。

联立式(5)、式(7)即可求得任意时刻胶囊受到的流体力和力矩。

2.3 动力学建模及简化

胶囊在流体环境运动时还可能会受到一些不稳定力,这些力对于胶囊影响不大,在本文中忽略不计[12]。

胶囊在流体环境下胃肠道表面的6自由度运动的牛顿-欧拉动力学方程为

(9)

Jx、Jy、Jz分别为胶囊绕x、y、z轴的转动惯量,同时有Jx=Jz。

式(9)方程过于复杂,实际上可以进行适当简化和假设。简化和假设如下:

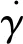
b.胶囊仅在胃肠道表面运动,在z轴方向位移很小,可视为无位移,即uz=0,Fz=0。

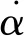
胶囊动力学模型可简化为

(10)

其中,有

(11)

3 胶囊姿态稳定性仿真分析

胶囊在运行过程中,由于姿态调整以及外界干扰发生摆动,姿态摆动将影响移位精确性甚至移位能否完成,因此,在选取控制参数时应保证胶囊姿态可快速稳定。

在表1的控制参数下,利用四阶龙格库塔算法对式(10)的动力学方程求解。

表1 数值计算主要参数

胶囊姿态角以及胶囊滑滚速度随时间变化曲线如图4所示。从图4中可以看到,胶囊的姿态角在短时间的姿态调整后均收敛为0,沿y轴的速度分量uy稳定在0,而沿目标方位x轴的速度分量ux则稳定在22.25 mm/s,此时的滑转率为88.2%。图4表明,胶囊在经过短时间的姿态调整后,姿态稳定,以连滚带滑的滑滚运动形式稳定前进。下面将分析影响胶囊姿态稳定性的因素。

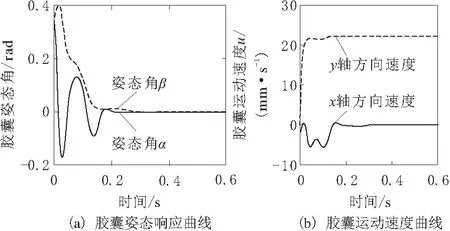
图4 仿真结果

不同磁场转速下胶囊姿态角α动态响应曲线如图5所示。曲线表明,随着磁场转速的提高,胶囊的姿态角的振荡幅值以及达到收敛的响应时间均有所下降,表明了胶囊姿态稳定性的提高。实际上,胶囊的滑滚运动与陀螺效应类似,提高转速后,小外力对胶囊旋转方向的影响减小,即摆动减小,稳定性提高。但磁场转速也不可无限提高。在实验中发现,在高转速时,经常发生丢步现象。同时考虑到磁场转速的增加也会提高胶囊的滑滚速度,在胃肠道诊疗时,过高的运动速度不利于诊断的全面性。因此,推荐使用的磁场转速范围为2π～12π rad/s。

图5 不同磁场转速胶囊姿态角动态响应曲线

不同流体粘度下胶囊姿态角α动态响应曲线如图6所示。流体粘度取值0.140 Pa·s时,胶囊的姿态角呈发散趋势,表明在该流体粘度,胶囊姿态不能稳定,最终将导致胶囊失控。流体粘度取值0.145 Pa·s时,胶囊姿态角呈周期振荡趋势,此时胶囊呈周期性摆动,可完成滚动行走,但行走轨迹为沿目标轨迹左右晃动,控制精度较差。流体粘度取值0.180 Pa·s时,胶囊姿态角约在1.6 s左右收敛,表示胶囊经1.6 s的姿态调整后即可稳定沿目标方位前进,控制精度大幅提高。显然,在表1的控制参数下,流体环境的动力粘度应保证在0.145 Pa·s以上,胶囊才可实现滚动行走。而要提高胶囊控制精度和效率,减少不必要的姿态调整时间以及在姿态调整过程中受到外界干扰,流体的动力粘度应保证在0.180 Pa·s以上。

图6 不同流体粘度胶囊姿态角动态响应曲线

不同磁场强度幅值时胶囊姿态角α动态响应曲线如图7所示。

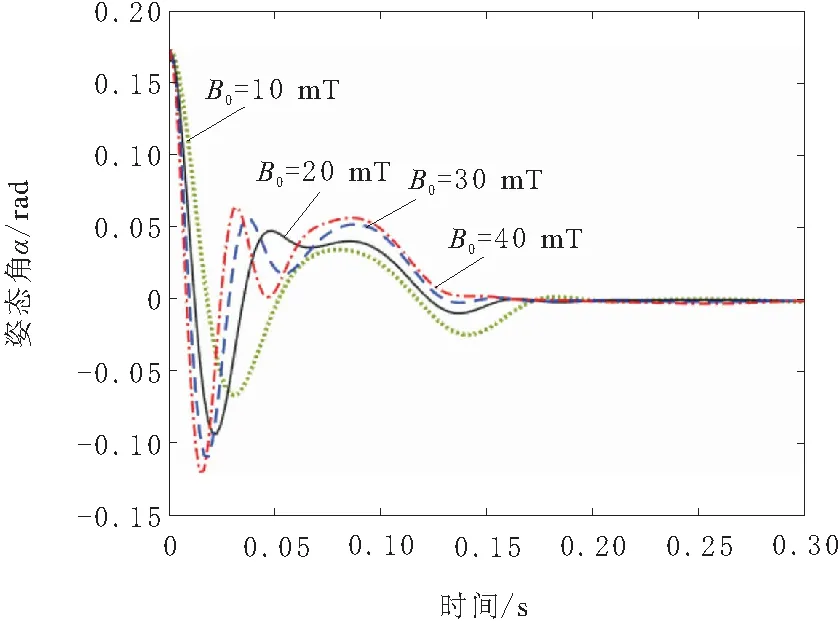
图7 不同磁场强度胶囊姿态角动态响应曲线

由图7可知,随磁场强度幅值B0的增加,胶囊姿态角α的振荡幅值略有增大,而响应时间略有减小。即使磁场强度幅值B0取值大于胶囊正常驱动所需要的磁场强度幅值的40 mT时,胶囊姿态仍可快速收敛。因此,磁场强度幅值正常取值时,对胶囊姿态影响不大。在选取时应首要考虑满足胶囊驱动的最小磁场强度幅值,然后略大于该值即可。

对于最小磁场强度幅值的计算可将胶囊运动的三维模型简化为平面模型,即忽略胶囊的摆动。简化并考虑稳态时的动力学模型为

(12)

式(12)表明,当磁场转速ω0一定时,达到稳态后滑滚速度ux也随之确定。在ux变化不大时,对式(12)的影响不大。为了简化计算,取胶囊的滑转率为90%。由于转差角受耦合磁矩以及流体力矩共同作用,可在(0°,90°)内调整。当磁矩矢量幅值m0固定,转差角σ取90°时,所需的磁场强度幅值B0最小,即最小磁场强度幅值Bmin以及滑滚速度ux计算式分别为:

(13)

(14)

在计算Bmin时转差角σ取90°,但实际上,过大的转差角易使胶囊转速无法跟随磁场转速,即发生丢步现象。同时在启动阶段,由于胶囊与胃肠道接触,此时胶囊所受到的阻力矩较大,因此,在选取磁场强度幅值时应略大于最小磁场强度幅值。推荐选用的磁场强度幅值为最小磁场强度幅值的1.5倍左右,即B0=(1.4～2.0)Bmin。在控制参数的选取应首先根据需要的胶囊运行速度,选择合适的磁场转速,再根据式(13)、式(14)选择合适的磁场强度及流体粘度等参数。

4 实验

为了验证上述理论内容,研制了电磁线圈及其控制系统以及胶囊内窥镜样机,如图8所示。胶囊样机半径7.5 mm,质量4.0 g。

图8 实验平台

磁场转速为3π rad/s、流体粘度为0.5 Pa·s时胶囊样机姿态变化如图9所示。可以看到,经过约2.417 s姿态调整完毕,胶囊进入稳定滑滚运动。

图9 胶囊姿态调整实验图像

改变控制参数,胶囊姿态调整时间及滑滚速度如表2所示。

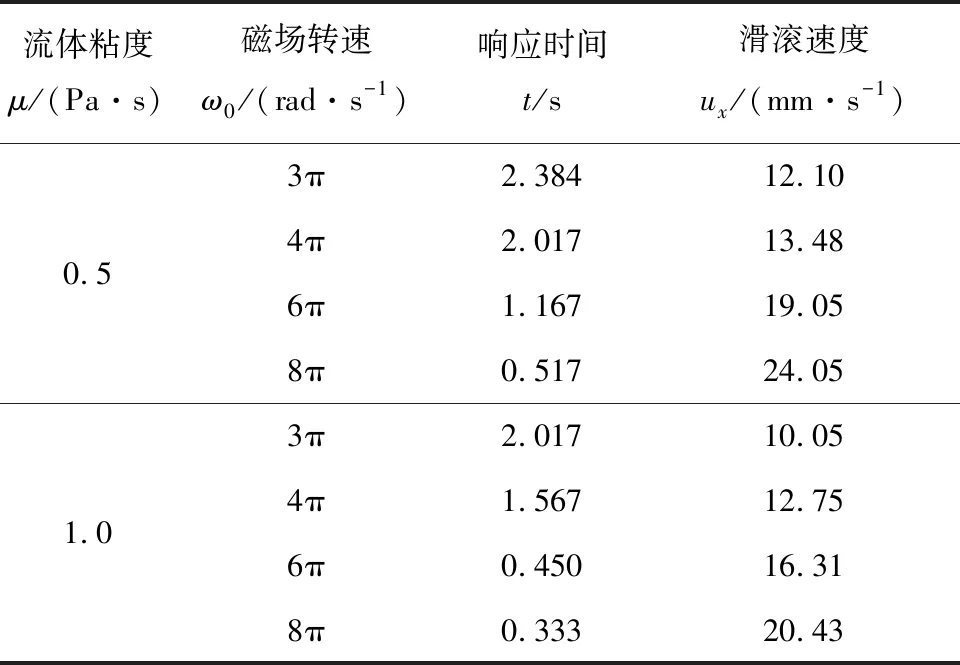
表2 实验数据

实验结果表明:胶囊姿态随磁场转速以及流体粘度的增加而增大,符合上述理论研究内容;胶囊在合适参数控制下可实现姿态稳定的滑滚运动,姿态调整时间短,前进速度慢,控制灵活方便,利于胶囊内窥镜的诊疗一体化。

5 结束语

本文对双半球胶囊内窥镜在流体环境下滚动姿态稳定性进行了研究,研究表明:胶囊可实现流体环境下姿态稳定的滑滚运动,姿态调整时间短、前进速率低;随磁场转速、流体粘度的提高,胶囊姿态稳定性增强。本文为双半球胶囊内窥镜流体环境下运动性能研究提供了参考依据,并为双半球胶囊内窥镜活检、施药等功能的实现奠定了一定的基础。今后,将对双半球胶囊流体环境精确控制、精准定位进行研究,并着手设计活检、施药等功能结构,为实现双半球胶囊内窥镜系统诊疗一体化操作奠定基础。