油画相似度的表面光场特征点分布鉴别

肖照林，孙彤鑫，张晶瑞，金海燕*

1.西安理工大学计算机科学与工程学院，西安 710048；2.陕西省网络计算与安全技术重点实验室，西安 710048

0 引言

油画具有可用颜料的薄厚体现所绘制对象的形态、层次和质感的特点。在不考虑成本与效率的前提下，可依据颜料厚度及其空间分布实现对油画进行相似度鉴别，例如采用非接触式表面粗糙度扫描技术（Claudia，2016）。然而，非接触式表面粗糙度扫描通常需要主动光源照射，故此类方法仍会对油画造成一定程度的损害。鉴于颜料厚度差异，导致油画表面存在非朗伯效应（Fachada等，2021）。该效应也可作为鉴别其相似度的依据。但是，采用相机直接拍摄难以采集这种微弱的的非朗伯效应。针对上述问题，本文提出一种采用光场成像技术对油画进行相似度鉴别的新方法。

与经典成像系统不同，光场成像系统不但能够记录传感器平面的光强分布，还能够记录入射光线的角度信息（Qi 等，2022）。这使得光场成像系统具备数字重聚焦、景深和光圈计算可调（Ng，2006）、场景深度可计算（Li 等，2021）、易检测显著目标（刘亚美 等，2020）等一系列新颖的成像效果。目标表面的非朗伯特征也可由光场角度信息进行描述，例如采集CD 唱片、玻璃制品、光泽陶瓷等表面的角度域差异。为了进一步放大油画表面微弱的非朗伯效应，本文采用微透镜阵列板增强了其表面光场（surface light field）的角度域变化，并采用Illum光场相机有效采集了这种角度域变化，如图1所示。

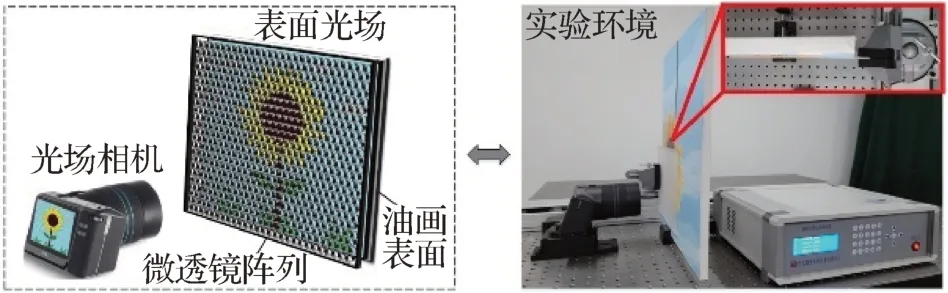
图1 油画表面光场生成与采集系统Fig.1 The proposed oil painting surface light field generation and acquisition system

在提取表面光场特征点的基础上，本文提出一种以特征点的几何分布定量计算油画相似度的方法。本文主要贡献如下：1）针对油画表面的非朗伯特性，提出采用微透镜阵列放大表面光场的深度差异，并且设计了可用于油画相似度检测的多角度表面光场生成与采集系统；2）为了提高对油画表面光场差异的定量计算的准确性和鲁棒性，提出光场角度域变化的特征点，以特征点的空间分布度量表面光场的相似性。基于油画表面真实光场数据，本文验证了基于角度域变化特征点分布的相似性度量方法在相似性计算准确性与可区分性上具有明显优于传统特征点匹配计算方法。

1 相关工作

1.1 油画相似度的鉴别

对油画年代确认、作者认定、画作防伪等问题一直是艺术品收藏界关注的焦点。传统人工鉴别方法需分析其绘画风格、技法特点、画家所处时代背景和画家签名等信息（寒风，2007），对鉴别人的主观经验要求极高。

随着光谱分析技术的发展，研究人员利用光谱仪对油画颜料进行分子特性分析，可对特定年代的画作进行鉴别。Benoy（2007）早期研究人员提出用拉曼光谱仪对油画颜料中的黄丹素以及植物衍生酶进行分析，成功鉴别了文艺复兴时期的油画作品（朝阳，2007）。然而，上述油画的鉴别手段仍存在成本高昂且依赖专业经验的问题。

21 世纪以来，图像处理技术也得以广泛应用于油画的鉴别。Widjaja 等人（2003）提出对画作表面斑块构建色彩映射表，并采用支持向量机分类方法对油画作者进行鉴定。王倩（2015）提出融合多种图像特征的深度学习油画真伪鉴别方法。苏雪薇（2020）提出融合油画颜色特征和形状特征的油画特征差异计算方法。Yu（2021）提出基于智能视觉检测模型的油画真伪鉴别方法。但是，此类图像处理方法均依赖于对色彩二维空间分布分析，较少关注油画颜料厚度差异。

1.2 表面光场及特征提取

双平面光场是采用直线与两个平行平面焦点的4 维参数描述空间中光线的位置和方向信息的参数化表示。L(u，v，x，y)表示光场的一条光线采样，L为光线强度，(u，v)表示位置信息，(x，y)表示方向信息。与传统成像不同，光场相机在传感器组件前有一组微透镜阵列，采用微透镜阵列平面与传感器平面构成双平面，从而得到4 维参数化的光场。由于光场数据的高可计算性，使得光场成像可实现数字重聚焦、视点可变和景深可调等新颖成像效果。

基于光线直线传播不衰减假设，Levoy 和Hanrahan（1996）提出平行双平面参数化方法对7 维全光函数（Gershun，1939）进行4 维参数化。Ng 等人（2005）提出在单反相机传感器前放置一个微透镜阵列以实现便携式的光场采集，并采用傅里叶切片成像理论降低了光场重聚焦的计算复杂度。针对物体表面光场重建问题，Wood等人（2000）提出了物体表面光场的构造、压缩和交互式渲染处理框架，并实现了复杂光照条件下的表面光场重构。Miandji 等人（2011）提出一种可预计算的全局光照模型，实现了对物体表面光场的实时高质量渲染。为降低表面光场建模对精确几何模型的依赖，Jachnik 等人（2012）提出一种对目标物表面光场反射特性的高精度估计方法，实现了对非朗伯镜面反射表面的实时采集和渲染。Li等人（2018）进一步提出多视纹理优化方法对表面光场建模，该方法无需高精度几何模型即可构建目标的高精度表面光场模型。Oechsle 等人（2020）提出一种深度学习的方法，实现了从任意视点渲染出指定照明条件的高质量场景外观。在表面测量领域，Zhou 等人（2020）提出一种基于漫反射光源和偏振技术的光场测量系统，有效消除了镜面反射的影响，提高三维测量精度。Traxler 等人（2021）对比了光场测量与结构光测量、立体相机测量、激光线扫测量的差异，并指出光场测量对于深度感知能力更具优势。上述方法虽然关注非朗伯表面光场的高精度重建，但尚未涉及对表面光场识别和相似度计算问题。

随着研究人员对光场特征提取与处理的研究工作逐渐深入，Teixeira 等人（2017）提出将光场多视角图像上检测到的SIFT（scale-invariant feature transform）特征点投影至光场对极平面图像（epipolarplane image，EPI）空间，筛选并得到符合EPI 连续直线特征的稳定光场特征点。Dansereau 等人（2019）提出在光场焦点堆栈序列中进行SIFT 特征提取，并提出了对尺度和深度变化鲁棒的光场LiFF（light field features）特征描述子。基于傅里叶视差分层表示，Xiao 等人（2021）提出一种具有尺度和深度鲁棒性的光场FDL-HSIFT（Fourier disparity layer-based Harris-SIFT feature）特征。Tsai等人（2019）分析了由物体折射导致的光场EPI 非线性采样分布特性，并提出了光场EPI空间的折射特征点检测方法。

受上述光场特征相关工作的启发，本文提出一种针对油画表面光场特征点分布的相似度量化计算方法，利用油画表面光场的非朗伯特性实现对其相似度的有效鉴别。

2 油画表面光场采集与特征点提取

表面光场的采集原理如图2 所示。由于采用单一角度拍摄模式，传统成像系统难以获取表面光场的非朗伯效应。受拍摄距离、成像分辨率及成像孔径等因素的影响，即使采用多角度方式拍摄油画表面，仍难以有效捕捉仅由颜料细微厚度差异引起的微弱非朗伯效应。如图2（a）所示，相机光心到油画表面距离为d，颜料细微厚度差异的均值为s，当d≫s时，油画表面主要呈现朗伯特性，即颜料厚度对图像视角变化的影响有限。

图2 表面光场的采集原理Fig.2 The acquisition principle of the surface light field（（a）Lambertian surface；（b）non-Lambertian surface light field；（c）the optical design model of the acquisition system）

2.1 油画非朗伯表面的构建与采集

为了放大油画表面的非朗伯效应，本文提出在距离油画表面为a的位置放置一块焦距为f的微透镜阵列板，油画表面位于微透镜的一倍焦距处，如图2（b）所示，其中i代表对应不同相机c的成像。此时，微透镜与油画表面形成具有唯一性的强朗伯表面光场。当满足f=a+s时，微透镜的出射光线将近似源自油画表面的相同点；反之，则出射光线源自油画表面的不同点。由此，采用这种前置微透镜阵列的方案可以有效放大颜料厚度差异所带来的非朗伯效应。

依据中光场变换理论（Liang 等，2011），本文将4维光场L(u，v，s，t)简化至二维L(u，s)以便于分析，如图2（c）所示。具体为

原始光场LF0的颜料厚度微弱变化经过Rf折射放大仅与微透镜焦距f相关。微透镜阵列板置于油画表面一倍焦距位置（即微透镜实像与虚像的分界点），实验中微透镜焦距为5 mm，仅略高于微透镜阵列板自身厚度。此时，微透镜上端面出射的光线角度域变化对颜料厚度变化敏感，该表面光场具备明显非朗伯特性。

上述过程构建和采集的油画表面光场数据如图3所示。图3（a）为一个光场的特定视角图像，也称子孔径图像（sub-aperture image，SAI），图3（b）为该视角的像素点与其他SAI上对应点的差异量化结果，即角度域变化的量化结果。图3（c）是角度域变化明显的特征点分布图。由图3可见，角度域变化特征点为油画表面且具有复杂纹理，且非朗伯特性被微透镜阵列放大后，能够有效被光场相机所记录的点。下文将详细介绍光场角度域变化的特征点提取过程。

图3 光场角度域变化特征点示意Fig.3 Light field feature points with large angular variations（（a）a given sub-aperture image；（b）the quantization of angular variation of pixels；（c）feature points with large angular variations）

2.2 光场特征点角度域变化的提取

为了降低成像渐晕和离轴畸变对特征提取的影响，仅选取成像质量较好的中心行SAI，并仅在SAI中心400 × 400 像素的区域进行特征点提取。针对一个特定像素位置(i，j)，以像点I(i，j)为中心，在SAI上半径为r区域的均值M(i，j)为

由于角度变化和视差的存在，任意两个不同SAI上像素点的角度域差异可由D(i，j)计算。具体为

在筛选后的特征点集合F 内，特征点均为其所在邻域Ω(i，j)内角度域差异的最大值点。

3 基于角度域变化特征点分布相似性度量的表面光场识别

通过对油画表面光场非朗伯特性的分析，一幅油画的表面光场角度域变化被微透镜阵列放大后，其角度域变化较大的特征点分布具有唯一性。因此，本节提出基于一种角度域变化特征点分布的油画表面相似性量化计算方法。

3.1 角度域变化特征点分布的相似性度量

经典特征点匹配计算常以特征向量的距离作为相似性度量，以量化一对特征点在特征空间的近似程度。然而，受到噪声、相似纹理及计算方法局限性的影响，采用特征点局部信息对整幅油画表面光场的相似度进行度量并不准确。因此，与对比单组或多组特征点对的相似度不同，本文提出计算角度域变化特征点的分布相似度，作为表面光场相似度识别的依据。

为了有效描述表面光场特征点的整体分布，在计算和筛选角度域变化较大特征点的基础上，利用K-Means 聚类算法（Bock，2007）对特征点分布进行多边形描述。首先，在400 × 400 像素的中心区域，选择K个相隔较远的像素点作为聚类中心的种子点；随后，利用K-Means 聚类算法对所有特征点进行聚类计算，其中距离计算采用欧氏距离，具体为

式中，d表示数据点与聚类质心之间的像素距离，K为聚类的类别数量，μi为第i个类别的聚类中心。最终，将K-Means 聚类后得到的K个聚类中心μi相连得到一个表示表面光场特征点分布的多边形结构，如图4所示。

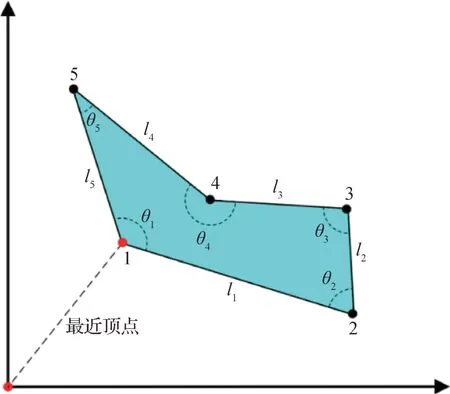
图4 特征点分布的相似性多边形示意Fig.4 Similarity polygon of feature points distribution

依据上述多边形的相似度对表面光场进行识别。表面光场特征点分布多边形的相似程度SD的计算式为

式中，SL和SA分别表示多边形的边长相似度和角度相似度，具体为

式中，SL表示两多边形图像的边长相似度，SA表示两多边形图像的角度相似度。如图4 所示，长度向量表示为 L(l1，l2，l3，l4，l5)，角度向量表示为A(θ1，θ2，θ3，θ4，θ5)。由上述定义可知，当SD较大时则表示两油画表面光场相似。反之则代表油画的相似度较低。

3.2 表面光场识别

在提取角度域变化特征点的基础上，依据其分布对油画表面光场进行相似度计算，其大致过程如图5所示。

图5 表面光场相似度计算的概要图Fig.5 An overview of similarity computation for the surface light field

首先利用光场相机对油画表面光场进行采集。进而，对中心行子孔径图像中非朗伯效应进行分析，提取随视角变化呈各向异性的角度域变化特征点集合。最后，通过计算光场间角度域变化特征点的分布相似度，完成对油画表面光场的相似度评价。

算法1：油画相似度计算。

输入：表面光场数据LF1，LF2，视差p，特征点变化阈值δ，最大迭代次数tmax，相似度阈值α。

输出：油画鉴别结果SD。

1）对LF1和LF2计算；

2）提取中心行子孔径图像序列，转换为灰度图像并剪裁中心区域，选择左视角vl和右视角vr；

3）根据式（2）计算vl和vr上像素点I(i，j)的邻域像素均值M(i，j)；

4）根据式（3）计算vl和vr视差p的像素点I(i，j)的差异D(i，j)；

5）得到光场候选特征点集合Fc={(i，j)|D(i，j)>δ}；

6）采用非极大值抑制由Fc计算最终光场特征点集合F；

7）对LF1和LF2各自得到的F计算；

8）进行最大迭代次数为tmax的K-Means 聚类分析，得到最终聚类质心点集合μ；

9）连接μ中的点构成多边形；

10）对LF1和LF2各自得到的多边形计算，使用式（6）计算表面光场相似程度SD。

4 实验结果与分析

4.1 油画表面光场的数据采集

为了测试所提出的油画相似性度量方法，针对真实油画设计了一套表面光场数据的采集系统，如图6所示。

图6 油画表面光场采集系统Fig.6 The oil painting surface light field acquisition system

该系统采用Illum 光场相机对目标油画进行垂直拍摄，该光场相机可采集空间分辨率为541 × 434像素、角度分辨率为15 × 17 像素的光场数据。在油画表面靠近相机一侧放置一块厚度为2.0 mm 的微透镜阵列板，其单个微透镜的焦距为3.0 mm，油画表面距离微透镜阵列板约1.0 mm。此时，油画表面位于微透镜1 倍焦距位置，微透镜出射至相机的光线可近似认为平行光。相机光心到微透镜阵列板的距离约为0.2 m。此外，采用平移台及限位器对微透镜阵列与油画表面的距离进行精确调整和控制。为了确保照明的恒定与均匀性，本文采用漫反射灯箱在相机后方距离油画约1 m处进行照明。

此时，微透镜阵列与油画表面形成了特定的表面光场，且微透镜阵列有效放大了油画表面颜料厚度起伏所导致的非朗伯效应。采用light field toolbox（Dansereau 等，2013）对光场数据进行白平衡及图像畸变的标定和校正，以降低预处理阶段数据色彩及几何失真对检测结果的影响。

采集数据集包括30 组油画不同区域的表面光场数据，每组数据中将表面不存在起伏的数据记为D，存在起伏差异的数据记为。与此同时，为了对比微透镜阵列对非朗伯效应的放大效应，对D和分别在使用微透镜阵列和不使用微透镜阵列情况下拍摄了对应的光场数据，分别为DM。其中，使用微透镜阵列记为M，不使用微透镜阵列记为。为了验证微透镜阵列与油画表面间距变化对表面光场的影响，本文对DM情况扩大间距0.5 mm 后拍摄，记为DM-0.5。由此，30 组表面光场数据共包含DM、和DM-0.55 种情况的光场数据，如图7 所示。由图7（b）可见，采用微透镜阵列可有效放大颜料厚度微弱变化引起的非朗伯特性。

图7 油画表面光场数据集Fig.7 The dataset of oil painting surface light fields（（a）7 groups of oil painting surface regions；（b）light field data collection results in 5 cases ）

4.2 表面光场相似度计算量化指标对比

首先，采用交并比（intersection-over-union，IOU）、相似度系数（Dice similarity coefficient，DSC）评价指标对比不同方法的相似度计算结果。理论上，IOU和DSC值越接近1.0，表示对比区域越接近，反之则代表差异明显。依据3.1 节所述方式提取表面光场特征点分布多边形，当颜料厚度存在轻微变化（）时，该多边形描述存在明显差异，如图8 和图9所示；反之则相似度很高。

图8 DM组光场特征点分布多边形的可视化结果Fig.8 The polygonal distribution of feature points in DM dataset

图9 组光场特征点分布的多边形可视化结果Fig.9 The polygonal distribution of feature points in dataset

为进一步分析不同度量方法对特征点分布相似度的计算差异，将IOU 和DSC 相似性度量与本文所提度量的量化计算进行对比，结果如表1 所示。由于两次拍摄震动、噪声及光照等因素影响，虽然图9中的表面光场相同，但其相似度计算结果仍会存在一定差异。由表1 可见，在计算相同表面光场相似度时，本文方法具有最高的平均相似度。相反，当表面光场存在差异时，本文所提方法相似度计算结果显著低于IOU 和DSC 方法，故本文方法对表面光场差异计算具有较高的区分度。

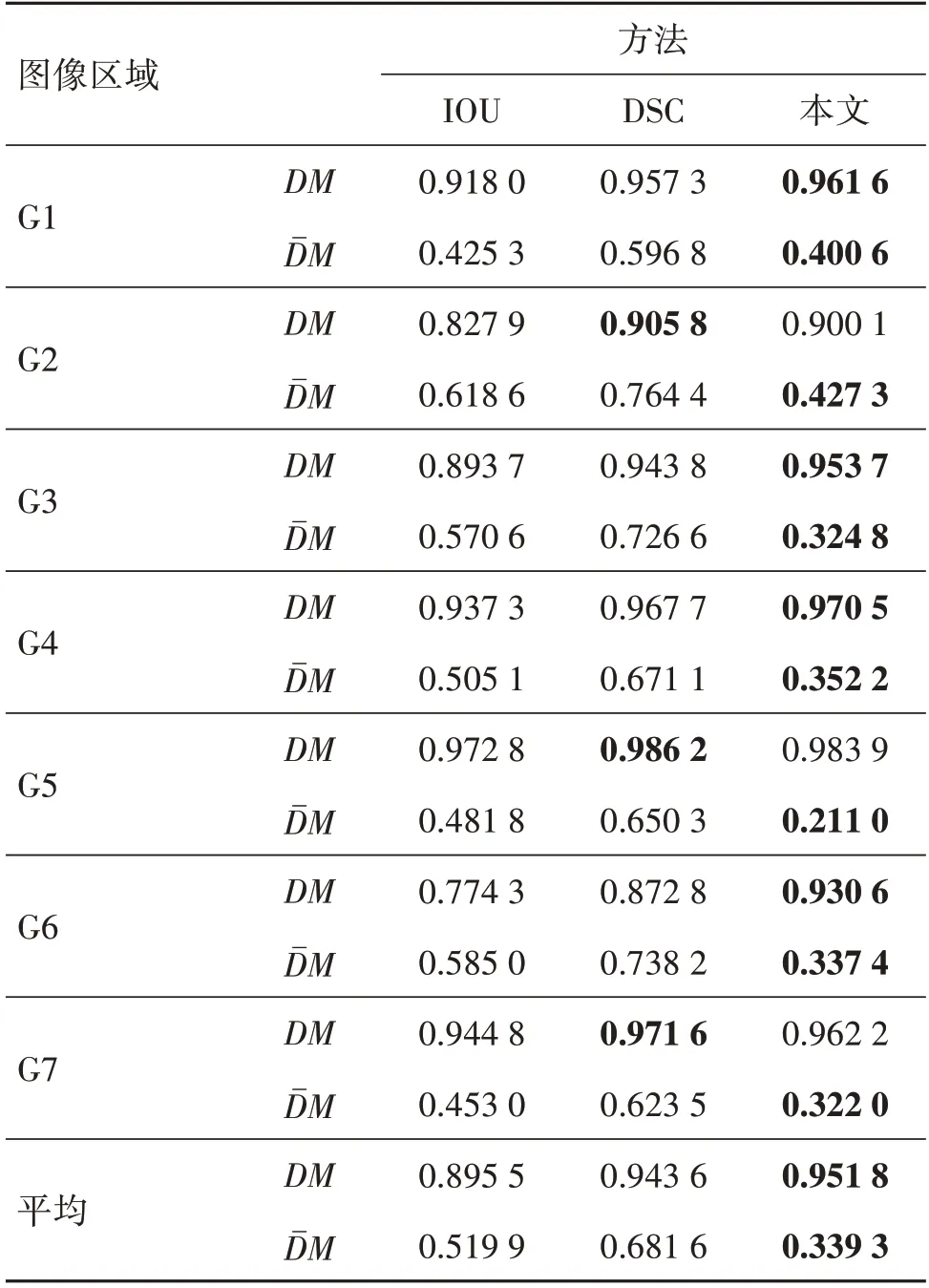
表1 表面光场相似度的量化计算指标比较Table 1 Surface light field similarity computation with different quantitative indexes

前文中特征点分布多边形的边数等于K-Means聚类中心数K，而边数设定对计算特征点的相似度具有较大影响。K取值较大时，聚类中心增加会导致算法的稳定性降低，即使同一光场表面多次采集的检测结果也会存在一定差异；相反，K取较小值时，算法对表面光场细微变化引起的特征点分布变化敏感性降低。为了选择恰当的K值，通过实验比较K值变化对DM组和组数据平均相似度的影响。其结果如表2 所示，当K=3 时组平均相似度较高，这代表算法对表面光场细微变化的区分度不足。当K=6和K=7时，虽然组相似度差异区分较为明显，但是DM组相同表面光场检测结果的一致性不足，即算法稳定性较差；当K=5时，同时满足了算法在DM组检测的稳定性，以及在组检测表面光场变化的敏感性。

表2 K值对相似度计算的影响分析Table 2 Similarity computation results with different K

综上，本文对角度域变化特征点的聚类中心数K采用经验选取方式，依据采集系统差异及数据集不同，K取值不同对相似性计算的影响较大。

4.3 表面光场特征检测与识别算法的对比分析

为验证本文提出的特征检测算法对鉴别油画相似度的优势，将所提算法与传统SIFT 特征检测方法（Lowe，2004）、光场LIFF 特征检测方法（Dansereau等，2019）及FDL-HSIFT 方法（Xiao 等，2021）进行对比。如图10（a）所示，当不采用微透镜阵列时（和DˉMˉ），细微起伏引起的表面光场变化并未引起特征点匹配的显著差异；在采用微透镜放大非朗伯效应后（DM和），其特征点匹配的差异明显（绿色线条代表匹配，红色线条代表不匹配）。受成像噪声、震动及光照等因素影响，3 组数据不匹配特征点的分布差异较大，这导致采用传统特征点匹配检测难以准确反映表面光场的变化。因此，提出采用不匹配特征点分布变化作为评判依据。如图10（b）所示，虽然DM组特征点提取结果并不相同（第3列和第4 列），但是采用本文算法提取的相似性多边形却可保持高度一致；反观组，虽然部分角度变化特征点仍存在一致性；但变化特征点空间分布差异可有效反映出表面光场的变化。由此可见，相比于采用特征点匹配数量的方法，采用变化特征点空间分布作为油画表面光场相似性鉴别的度量依据更具合理性。

图10 特征点匹配方法与本文方法检测油画表面变化的对比Fig.10 The surface variation detection comparison among the proposed algorithm and other feature matching algorithms（（a）variation detection based on feature point matching algorithms；（b）visualization results using the proposed detection）

对图10 中数据的量化计算结果见表3 和表4。值得注意的是，对于DM组，评价指标越接近1 越优；而对于组则与DM差异越大越优，故和DM组评价指标的平均相似度差值越大，代表可区分性越强。对表3 和表4 分析可知，在不采用微透镜阵列的情况下，基于特征点的方法同样难以区分各组油画表面细微起伏所造成的影响，因此和特征点匹配的可区分性不足。在使用微透镜阵列放大非朗伯效应后，所列方法对DM和具有较强的可区分性。综上所述，本文提出采用微透镜阵列放大油画表面非朗伯效应，并基于表面光场特征点分布计算表面光场相似度更为合理，能够有效区分出油画表面起伏细微差异所导致的角度域变化。

表3 对比采用不同特征提取方法计算和DM表面光场的相似度Table 3 Similarity calculation comparison of different feature extraction on and DM

表3 对比采用不同特征提取方法计算和DM表面光场的相似度Table 3 Similarity calculation comparison of different feature extraction on and DM

注：加粗字体表示各列最优结果。

表4 对比采用不同特征提取方法计算和表面光场的相似度Table 4 Similarity calculation comparison of different feature extraction on and

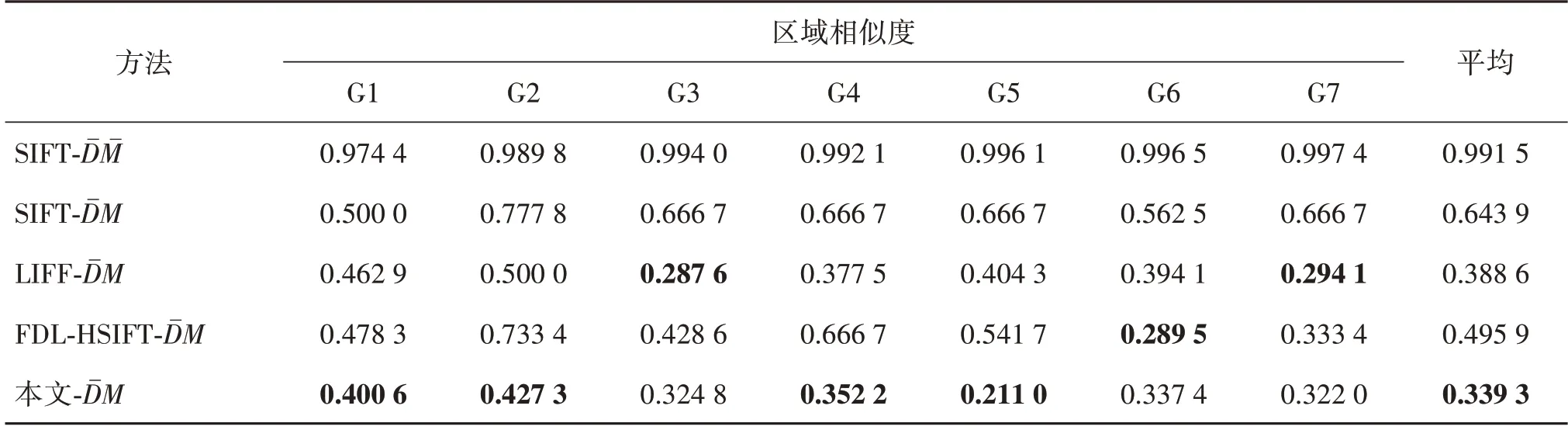
表4 对比采用不同特征提取方法计算和表面光场的相似度Table 4 Similarity calculation comparison of different feature extraction on and

注：加粗字体表示各列最优结果。

4.4 微透镜阵列位置变化对表面光场采集及油画相似性计算的影响分析

由于微透镜阵列相对于油画的位置变化会直接影响表面光场生成，因此进一步分析了两者间距变化对相似性鉴别的影响。如图11 所示，两组DM-0.5数据是当微透镜阵列板与油画表面间距扩大0.5 mm 时的对比实验，依据所提的相似性计算方法，其相似度值具有明显可区分性，两组相似度评价量化指标均小于0.9。因此，本文方法可有效检测大于0.5 mm 的油画表面细微起伏。油画表面与微透镜阵列间距远大于微透镜的一倍聚焦时，光场相机所拍摄的图像会逐渐模糊，此时表面光场特征相似性的量化计算稳定性降低，故本文建议微透镜与油画表面的间距在微透镜的一倍焦距处，其油画表面起伏在[0.5f，1.5f]范围内。此外，微透镜及油画位置偏差会影响本文算法的检测精度，故本文实验均近距离拍摄靠近夹具的微透镜和油画部分，并仔细测量了系统各部分之间的距离，以减少位置偏差带来的影响。但是文中系统仍为原理验证系统，如需满足实用化要求，仍需更精确的控制系统调节成像端、微透镜阵列和油画三者的距离。

图11 微透镜阵列与油画表面间距变化对检测结果的影响分析Fig.11 Detection analysis with the distance between the micro-lens array and the oil painting surface

5 结论

针对油画相似度鉴别问题，提出一种基于表面光场特征点分布的相似度量化计算方法。首先，该方法采用微透镜阵列放大油画表面的非朗伯效应，并基于光场相机搭建了针对油画表面光场的多角度采集系统。对多组真实油画的表面光场进行了采集实验，实验结果表明了采用微透镜阵列放大非朗伯效应的有效性。在此基础上，本文提取光场角度域变化特征点，并提出了计算特征点几何分布以度量油画相似性的新方法。相较于经典的基于特征点匹配的相似度计算方法，本文方法在真实油画数据集实验中具有更优的区分度，能够有效鉴别0.5 mm以上细微的油画表面变化。

由于采用微透镜阵列作为油画表面光场的生成装置，故本文方法具有一定适用条件，即微透镜与油画表面的间距在微透镜一倍焦距处，且油画表面起伏应在[0.5f，1.5f]范围内。由于微透镜及油画位置偏差会影响本文算法的检测精度，未来工作中可改进油画表面、微透镜阵列以及光场相机之间的距离控制系统，以提高光场采集的精确性和可重复性。此外，可采用角度域可编码光源改进采集系统，以强化油画表面非朗伯特征的角度域可观测性。

致谢感谢西北工业大学王庆教授和周果清副教授在表面光场采集问题上具有建设性的讨论与帮助。感谢法国国立计算机与自动化研究所（Institut National de Recherche en Informatique et en Automatique，INRIA）Christine Guillemot 教授对于表面光场特征提取方面的讨论与帮助。