利用括号表示法优化二叉树算法问题的研究

张加恩 吴凤英 梁玉林 杜少波

贵州商学院计算机与信息工程学院 贵州贵阳 550014

随着科技的提高,互联网行业快速发展。无论是对于想从事编程工作的科班学生,或是从事实际开发的从业者。若想写出较为复杂并且更加简洁高效的代码,都需要用到数据结构的知识。

而树作为数据结构学习中的一个重要的非线性数据结构,是在实际开发中经常用到的,其中二叉树是树结构中最重要的一个基本结构。在传统的算法中,我们构造二叉树的时候,是一个递归过程,使用了分治法的思想,即根据两种遍历序列确定当前树的根节点,左子树的两种遍历序列和右子树的两种遍历序列,再用相同的方法确定左子树和右子树的根节点。其他二叉树基础运算,如查询二叉树的深度、某一层有多少个节点以及查询有多少个叶子节点时候运用的都是递归函数。

但是递归函数本身有很多局限性,比如消耗的空间资源较大,所以递归的层数不能太多,这就在一定程度上限制了二叉数的大小。而本文采用了括号表示法去描述一颗二叉树的具体构造,对字符串进行遍历去运算有关二叉树的基础运算,从而解决了递归算法查询二叉树的一些弊端。

1 二叉树的构造算法

1.1 传统递归算法实现

二叉树具有顺序和链式两种存储结构,其中链式存储结构一般比较常用,本文通过设置二叉树的数据域、左链域和右链域来定义二叉树的结点类型,结点数据类型的C语言描述如下:

typedef int ElemType;//定义ElemType为int类型

typedef struct BTNode

{

ElemType data;//数据域为任意类型

struct BTNode*left,*right;//left和right分别为左链域和右链域

}*BiTree,BiNode;

//BiTree为二叉树结点的指针类型,BiNode为普通类型

根据所声明的二叉树结点类型,按照先序遍历二叉树的执行过程,先序序列创建二叉树,具体代码描述如下:

BiTree buildTree()

{

ElemType a;

BiTree root;

scanf(“%d”,&a);//输入结点的值

if(a==’ ‘)

root=NULL;//输入的字符为空格,返回空指针,证明该节点没有字节点

else

{

if(!(root=(BiTree)malloc(sizeof(BTNode))))//开辟一个大小为BTNode的空间,存放新节点

T->data=a;//给结点的数据域赋值

T->left=buildTree();

//给结点的左链域赋值

T->right=buildTree();

//给结点的右链域赋值

}

returnroot;//返回创建好的结点地址

}

如图1,如果使用常规算法构建这样一棵二叉树,需要调用buildTree()函数八次,递归层数最大要调到四层。

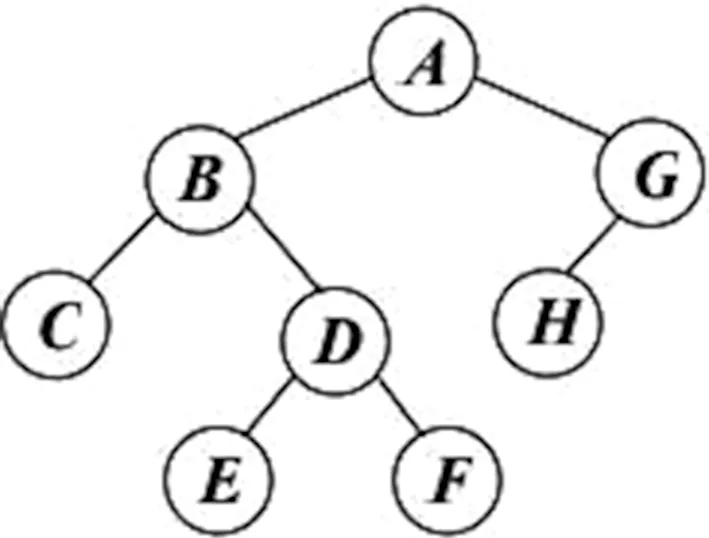
图1 二叉树示例

虽然常规的递归算法具有代码简洁、编写和理解容易等特点,但在运行时需要系统内部的栈来实现,因此执行需要消耗大量的空间和时间,运行效率较低。

1.2 用括号表示法实现

所谓括号表示法,就是一种用字符串体现二叉树各节点关系的一种表示方式。具体来说,如果一个节点还有子节点的话,在这个节点所代表的字母后面会跟着一对括号,这一对括号里面就是该节点子节点的信息。如果一个节点处在一个括号当中,用逗号分隔该节点和该节点的兄弟节点。

如上图1,用括号表示法表示出来的结果就为A(B(C,D(E,F)),G(H))。通过括号表示法,可以较为清楚地看见二叉树每一个节点所对应的关系以及层级,这样二叉树的大小就不再限制于递归函数层数的局限性了。

传统的括号表示法还有一点局限,就是对于只有右子树的情况表达不明确,如上图的H节点如果为右子树,和为左子树的情况无法区分。而本文将括号表示法进行了优化,只有在一个括号里面逗号右边的字母才表示上一个节点的右子数,所以如果一个节点它没有左子树的话,在优化后的括号表示法中依旧会写一个逗号,表示这个单一节点为右节点,如图1如果H结点为右子数,则会表示为A(B(C,D(E,F)),G(,H))。

同时,可以通过对这串字符串进行遍历,从而计算出想要的二叉数的数据,比如它的深度、某一层有多少个节点、叶子节点的个数等。

1.3 用括号表示法生成二叉树

用括号表示法生成二叉树时,使用了栈来存储未完成的结点,每次处理一个括号中的字符,如果字符为节点的data,则创建一个新的结点,并将其添加到父结点的左子树或右子树中,然后将其入栈。如果字符是右括号,则弹出栈顶元素,处理完毕后。最后返回根结点即可。

//通过括号表示法建立二叉树

TreeNode*buildTree(string s)

{if(s.empty())

{return NULL;}//根结点

TreeNode*root=new TreeNode(s[0]);//栈用于存储未完成的结点stackst;

st.push(root);

for(int i=1;i

{TreeNode*cur=st.top();st.pop();//处理左子树

if(s[i]!='('&& s[i]!=')')

{cur->left=new TreeNode(s[i]);

st.push(cur->left);}//处理右子树

if(i+1

{cur->right=new TreeNode(s[i+1]);

st.push(cur->right);}}

return root;}

2 利用括号表示法优化二叉树算法

2.1 查找二叉树深度

二叉树的深度就是二叉树有多少层,如图1,二叉树的深度为四。大部分情况下,传统查找二叉树深度的算法使用的是递归算法。算法逻辑为:一直查找某一个节点,是否还有子节点,直至没有为止。然后记录它的深度,然后把所有的节点全都查找完,最后输出记录下来的最大深度。

但是由于递归函数的局限性,所以本文用括号表示法去优化这个算法。因为在括号表示法中,如果出现了左括号代表该节点有子节点,深度加一。逗号的话代表该节点的兄弟结点,深度不变。如果是右括号的话,代表这一层已经结束,要返回上一层,所以深度减一。然后用一个记录变量,一直更新为最大值,最后输出即可。

C语言描述如下:

string BinaryTree;//用括号表示法记录二叉树

int Depth=1;//默认从根节点开始

int max;//记录最大深度

int BinaryTreeDepth(){

for(int i=0;i

{

if(BinaryTree[i]==’(’)

Depth++;//出现了左括号代表该节点有子节点,深度加一

if(BinaryTree[i]==’)’)

Depth--;//是右括号的话,代表这一层已经结束,深度减一

if(Depth>max)

max=Depth;//记录最大深度

}

return max;//返回二叉树深度

}

如果使用传统的递归算法,需要调用递归函数八次,但是用括号表示法去优化以后只需要调用一次函数,而且不浪费额外的空间花销,同时运算速度也得到了极大的提升。

2.2 查找二叉树某一层节点数

有时候对于一棵比较大的二叉树,有需求知道某一层的节点个数。如果使用传统的递归算法,需要遍历每一个分支到所需要的那一层,然后去统计该层的节点数量。

但用括号表示法优化该算法的时候,可以类比于查找二叉树深度的函数,设定一个定位变量,如果出现了左括号代表该节点有子节点,定位变量层数加一。逗号的话代表是同一层某一节点的兄弟结点,层数不变。如果是右括号的话,代表这一层已经结束,要返回上一层,所以层数减一。确定到所求层数以后统计节点数量即可。

C语言描述如下:

string BinaryTree;//用括号表示法记录二叉树

int Layers=1;//默认从根节点开始

int Num=0;//记录节点数

int BinaryLayersNum(int k){

//k是所求层数

for(int i=0;i

{

if(BinaryTree[i]==’(’)

Layers++;//出现了左括号代表该节点有子节点,深度加一

if(BinaryTree[i]==’)’)

Layers--;//是右括号的话,代表这一层已经结束,深度减一

if(Layers==k)

if(BinaryTree[i]>=’A’&&BinaryTree[i]<=’Z’)//只记录节点数(除去括号,逗号等符号)

Num++;//记录节点数

}

return Num;//返回二叉树某一层节点数

}

2.3 查找二叉树叶子节点数

在实际开发需求中,经常会需要查询一棵二叉树所有的叶子节点数。所谓叶子节点数,就是没有子节点的节点。在传统的算法中,都是用递归函数一直查询到某一个没有子节点的节点,然后记录,直到把整棵二叉树都遍历完成。

但是这种方式不仅在空间和时间的利用率极其低下,当二叉树比较大时,递归的层数无法达到那么多,所以导致无法计算。

用括号表示法优化该算法的时候,本文所改进的算法可以解决上述的弊端。通过括号表示法的性质可以得知,如果一个节点有子节点,该节点的后面一定会跟着一个左括号。如果没有左括号,就证明该节点是一个叶子节点,在算法中设置一个记录变量,记录叶子节点的个数。

C语言描述如下:

string BinaryTree;//用括号表示法记录二叉树

int Num=0;//记录节点数

int BinaryLeafNodes(){

for(int i=0;i

{

if(BinaryTree[i]>=’A’&&BinaryTree[i]<=’Z’)//只判断节点(除去括号,逗号等符号)

if(BinaryTree[i+1]!=’(’)//如果没有子节点

Num++;

}

return Num;

}

通过上述代码可以看出,改进后的算法只用遍历一次字符串就可以求得所有的叶子节点,极大地减轻了用递归函数所带来的时间和空间上的消耗,并且运算速度也比递归算法更快。

3 二叉树输出为括号表示法

通过上面的比较可以看出,经过括号表示法优化以后的算法运算速度较递归算法更快,同时极大节省了空间上的浪费。但对于已经建好的二叉树,需要输出为括号表示法,所以本文也提出了一种将二叉树输出为括号表示法的算法。

其过程是对于非空二叉树先输出根节点值,当存在左孩子节点或右孩子节点时,输出一个“(”符号。然后递归处理左子树,输出一个“,”符号,递归处理柚子树,最后输出一个“)”符号。

C语言描述如下:

void DispBTree(BiTree*bt){

if(bt!=NULL)

{

printf(“%c”,bt->data);

if(bt->lchild!=NULL&&bt->rchild!=NULL)

{

printf(“(”);

DispBTree(bt->lchild);

if(bt->rchild!=NULL)

printf(“,”);

DispBTree(bt->rchild);

printf(“)”);

}

}

}

通过上述算法,我们就可以将一个已经建立好的二叉树输出成一个用括号表示法描述的二叉树的字符串。然后通过对这个字符串的处理,我们就可以对本文所提到的几种关于二叉树的算法进行计算与使用。

4 结论

传统的二叉树算法都是用递归算法分析,但递归算法本身就着许多局限性。本文主要阐述了利用括号表示法改进二叉树算法的一些案例,除此之外,这种思想还可以用来改进求二叉树总结点的运算以及其他跟二叉树有关的运算。

本文对于传统二叉树的算法,与用优化后的括号表示法表示的二叉树算法进行了比较,本文分别设立了八节点、二十节点与五十节点的二叉树,在相同情况下,对两种算法所用的时间进行了比较,比较结果如图2所示。

图2 算法所用时间比较

实验使用编译环境为Dev-C++5.4.0版本,数据量是一棵比较小的八节点二叉树,如前文图1所示。通过在相同环境下,执行同样功能的程序。通过高精度时控函数QueryPerformanceCounter函数,测量程序运行时间精确到毫秒。

实验结果表明,求二叉树深度算法效率提高了18%。求二叉树叶子节点算法所提高效率为57%。可以看出,通过括号表示法改进的二叉树算法在时间上有较大的提升。同时,由于只用了一个字符串去存储,所以也节约了大量的空间。

在二十节点的情况下,两种算法所用的时间比较结果如图3所示。

图3 算法所用时间比较

从图3可以看出,当节点数中等的情况下,传统算法的时间复杂度较低,但是消耗的空间较大。优化算法时间稍微较长,但是消耗的空间更小。

在五十节点的情况下,传统算法由于递归函数调用次数过多导致栈堆溢出无法执行程序,而优化后的算法则不受二叉树大小影响。

基于这种思想,将原有运用递归算法所大量浪费的空间与时间方面进行改进,也为了进一步优化图以及其他有关树的算法提供了部分借鉴思想。