融合伺服增益优化的经济型数控机床圆轮廓误差补偿研究
孟繁喆
(柳州长虹航天技术有限公司, 广西 柳州 545002)
0 引言
经济型数控机床已广泛应用于汽车、石油、军工等机械加工行业,。此类机床机床结构成熟,但功能简单、性能较差,使得加工零件的圆轮廓精度无法保证[1]。 而圆轮廓误差的控制及补偿是保证零件圆轮廓精度的关键[2]。 因此, 经济型数控机床圆轮廓误差补偿方法的研究对提高其圆轮廓加工精度具有重要意义。
数控加工过程中, 产生圆轮廓误差的主要原因有机械结构误差、负载扰动以及伺服增益不匹配等[3-4]。基于上述原因,国内外学者提出多种圆轮廓误差补偿策略,可概括为如下三类:第一类,Koren[5]提出的交叉耦合控制器,可借由各轴间的影响来相互补偿直接减小圆轮廓误差,但控制器设计复杂,轮廓误差计算量大,导致系统响应速度慢;第二类,Tomizuka[6]提出的ZPETC 算法,通过降低跟踪误差进而间接减少圆轮廓误差,但由于死区、摩擦力、定位力等的干扰, 使得此类开环控制方法不能有效地改善系统的圆轮廓误差[7];第三类,通过调整各轴的伺服增益参数来优化其动态特性,进而降低圆轮廓误差。 如张彦方等[8]通过匹配双轴伺服系统增益抑制系统出现的动荡和抖动,进而降低圆轮廓误差;孙建仁等[9]通过理论推导,得出高的伺服增益或使两轴伺服增益尽可能相等对降低圆轮廓误差十分有用。 第三类方法较前两类方法有简单、稳定且易于实现等特点, 很适用于经济型数控机床的圆轮廓误差控制。
此外,由于经济型数控机床多以丝杠为传动件,而丝杠存在反向间隙误差会影响圆轮廓误差[10]。 因此,在优化伺服增益的基础上推导反向间隙误差对圆轮廓误差的影响机理, 并提出基于伺服增益优化及反向间隙补偿的经济型数控机床圆轮廓误差补偿方法。 在VMC850 数控机床X-Y 进给系统上验证该方法的有效性和可行性。
1 伺服增益不匹配产生的圆轮廓误差
XY 两轴在实际加工过程中圆轮廓误差如图1 所示,其中A、A' 分别为半径R 圆弧轮廓某时刻理论位置点与实际位置点,ΔR 为实际位置点A' 半径误差量; 当前X轴、Y 轴运动速度分量分 别 为Vx、Vy,Ex,Ey,跟随误差分别为Ex、Ey,角度α 为过圆心O 与理想位置点A 连线和X轴之间夹角。

图1 圆轮廓误差模型图
由图1 中几何关系分析得:
式中:Kx、Ky分别为X 轴、Y 轴伺服系统增益。 由于ΔR 为无穷小量,忽略ΔR2,则:
式(2)说明伺服系统处于稳态时伺服增益与轮廓误差的关系,由公式可知,当Kx、Ky增益同时减小时,轮廓误差也会减小。此外,在实际轮廓加工运动控制过程中伺服系统动态特性对圆轮廓误差的影响也不可忽视。
为研究伺服系统动态特性对圆轮廓误差的影响,设Kx、Ky分别为X 轴、Y 轴伺服系统闭环增益,Tx、Ty分别为X 轴、Y 轴时间常数,K 为系统闭环增益,T 为系统时间常数。 则X、Y 两轴联动系统运动方程为:
式中:Xc(t)、Yc(t)—t 时刻目标位置点;Xa(t)、Ya(t)—t 时刻实际位置点。
当XY 平面内两轴运行轨迹为半径R 圆弧时, 输入信号为:
式(5)为实际圆弧轨迹稳态解,根据Xa2(t)+Ya2(t)=(R+ΔR)2,略去高阶项ΔR2,得到t 时刻理想圆弧轨迹与实际圆弧轨迹之间误差ea为:
将式(5)代入式(6)后展开,由于Tω<1 ,略去其三阶以上项可得:
分析式(7)可知,在其余变量保持不变的情况下,增大Kx和Ky或者使Kx与Ky尽量相等都能降低t 时刻理想圆弧轨迹与实际圆弧轨迹之间轮廓误差ea;此外,增加Tx或Ty同样能降低轮廓误差ea。
2 反向间隙误差产生的圆轮廓误差
在以滚珠丝杠为传动部件的X-Y 平台中,反向间隙误差始终存在。由于X 轴、Y 轴在圆轮廓加工过程中需要不断改变运动方向, 所以反向间隙误差势必会影响圆轮廓误差。为分析反向间隙误差对圆轮廓误差的作用机理,假设X 轴、Y 轴伺服特性相同且K=1,X 轴、Y 轴的间隙误差量分别为2Δx和2Δy。 轨迹x1(t)、y1(t)的稳态解为:
假设起点位于xp(0)=rp-Δx,yp(0)=-Δy,则根据间隙非线性关系输入输出特性得到实际xp(t)、yp(t)为:
根据理想轨迹xc2(t)+yc2(t)=r2,设XY 两进给轴的方向误差分量分别为ex和ey,则半径误差er为:
将实际轨迹表达式(9)代入式(10)并简化后得半径误差er的表达式:
一般情况下间隙误差量Δx、Δy远远小于rp,故θx、θy很小,可忽略。则分析式(11)可知半径误差er在各象限内按照余弦规律变化,而在换象限处有一跳跃变化。
3 圆轮廓误差的补偿策略及实验
3.1 圆轮廓误差补偿策略
基于伺服增益优化及反向间隙误差补偿的圆轮廓误差补偿策略分为如下两步:
第一步, 依据伺服增益产生圆轮廓误差的机理对伺服增益进行调整,进而对圆轮廓误差进行补偿。 采用单因素法依次对位置比例增益、前馈增益、速度比例增益以及速度积分常数等伺服参数进行调整, 观察对应的响应曲线并选择出一组最优参数,如表1 所示。

表1 X/Y 轴伺服驱动器参数调整表
第二步,在伺服参数优化的基础上,基于自适应加减速反向间隙误差补偿法分别补偿X 轴、Y 轴的反向间隙误差,进一步改善圆轮廓误差。
3.2 实验平台
为验证通过优化伺服增益和反向间隙误差补偿降低圆轮廓误差方法的有效性,搭建如图2 所示的实验平台。该平台主要由VMC850 数控机床、 运动控制系统和雷尼绍QC20-W 无线球杆仪测量系统三部分构成。 实验选取数控机床的X-Y 平面进行测量,X 轴行程0~780mm,Y轴行程0~330mm。QC20-W 球杆仪的标称长度为100mm,行 程-1.25 ~+1.75mm,分辨率为0.1μm。

图2 实验平台
参照现行国家标准GB/T17421.4—2003 《机床检验通则第4 部分-数控机床的圆检验内容》,将实验分为三组: 第一组,在默认的伺服参数且未进行反向间隙误差补偿的情况下进行圆轮廓误差测量;第二组,伺服参数按表1 优化但未加入反向间隙误差补偿时进行测量;第三组,既优化伺服参数又进行反向间隙误差补偿,然后再测量圆轮廓误差。三组实验的因素对比表如表2。

表2 三组实验因素对比表
三组实验分别在顺时针方向与逆时针方向进行检验。结合数控机床X 轴、Y 轴行程与雷尼绍QC20-W 无线球杆仪设备条件选择测量直径D=200mm,进给率在常用速度段内选用F=400mm/min。 为减少随机误差,每组实验都在同等实验条件下重复3 次, 并以3 次测试结果的算术平均值作为实验结果。
3.3 实验结果与分析
依据实验条件, 分别按表2 实验条件对X 轴和Y 轴联动圆轮廓误差各进行3 次测量。 测量误差项主要包括逆时针圆偏差Gxy、顺时针圆偏差Gyx和圆滞后H,三组实验的测量结果如表3 所示。

表3 X-Y 进给系统圆弧轮廓精度评价表
将三组实验的结果进行对比分析可知: 第二组与第一组相比, 逆时针圆度偏差Gxy由0.0461mm 减少到0.0276mm,降低40.13%;顺时针圆度偏差Gyx由0.0397mm减少到0.0293mm,减少26.20%;圆滞后H 由0.0207mm 减少到0.0153mm,减少26.09%。 第三组与第二组相比,逆时针圆度偏差Gxy由0.0276mm 增加至0.0306mm;顺时针圆度偏差Gyx由0.0293mm 减少到0.0268mm,减少8.53%;圆滞后H 由0.0153mm 减少到0.0135mm,降低11.76%。三组实验的圆轮廓误差评价直方图如图3 所示。

图3 三组实验的圆轮廓误差直方图
由图3, 加入反向间隙误差补偿后圆度和圆滞后指标并没有明显改善,为进一步验证反向间隙误差补偿对圆轮廓误差的作用,分析图4 所示的圆轮廓误差诊断图。 对比图4(b)和图4(a)可见,经过伺服参数优化后,有效改善由伺服动态特性不匹配导致的圆轮廓误差剧烈波动, 有效减小机床圆度误差。 再将加入反向间隙补偿后的圆轮廓误差诊断图4(c)同图4(b)对比可知,加入间隙误差补偿能有效避免圆轮廓在换象限处的跳跃误差, 间接降低圆偏差和圆滞后。
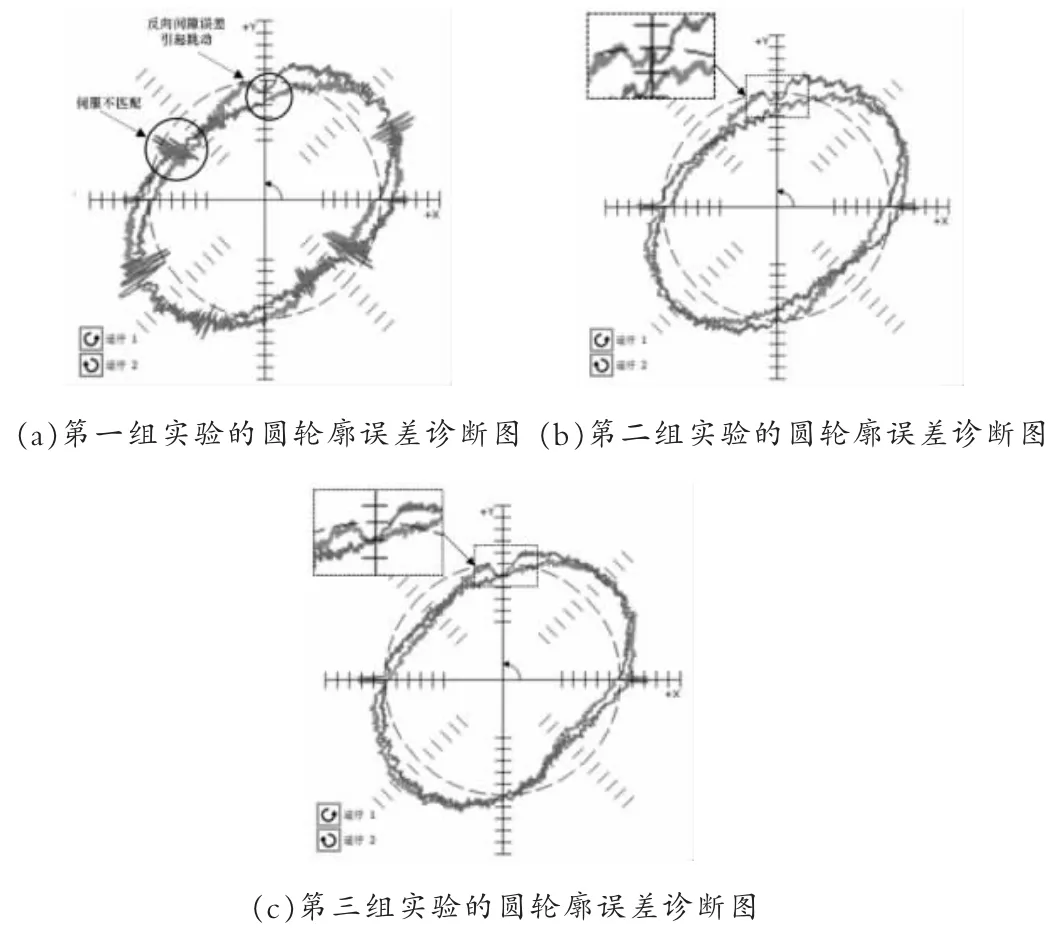
图4 三组实验的圆轮廓误差诊断图
4 结束语
以VMC850 数控机床XY 轴进行圆轮廓误差补偿研究,通过对伺服增益、反向间隙误差产生轮廓误差的机理进行推导, 并分别对比默认伺服参数且未加入反向间隙误差补偿、优化伺服参数但未加入反向间隙误差补偿、优化伺服参数且加入反向间隙误差补偿三组圆轮廓误差测量实验,得到如下结论:
(1) 基于伺服参数优化的圆轮廓误差补偿法以其操作简单、 不需改动现有硬件等特点可有效降低机床XY平面的圆轮廓误差。 对比未优化时,逆时针圆度偏差Gxy降低40.13%;顺时针圆度偏差Gyx减少26.20%。圆滞后H减少26.09%。
(2)反向间隙补偿相比于伺服参数优化,对圆轮廓误差评价指标Gxy、Gyx、H 等改善并不明显。 但对圆轮廓误差诊断图分析可知, 反向间隙误差补偿能有效避免圆轮廓在换向处的阶梯性跳跃现象。

