基于响应曲面法的超声挤压工艺参数优化*

常金鑫,贾海利

(1.天津职业技术师范大学 机械工程学院,天津 300222;2.天津市高端智能数控机床工程研究中心,天津 300222)

1 引言

航空航天领域大量轴类零部件通常在高温、重载和腐蚀性介质等复杂工作条件下使用,且长时间承受高载荷导致工作表面产生疲劳裂纹,极易引发零件疲劳失效[1-2]。其中,轴类零件的旋转疲劳强度是最主要的失效形式之一[3]。因此,迫切需要通过表面改性技术提高材料的抗疲劳性能,使其表面具有较低的粗糙度。

超声挤压技术是一种结合静挤压力和高频动态冲击力的表面光整技术。它在施加一定静压的基础上,通过施加超声波频率冲击,对材料表面产生塑性变形,可以显著改善表面形态和表面力学特性。与传统的挤压工艺相比,超声波挤压可以在表面材料上引入更深的硬化层,进而增强零件抗疲劳性能[4]。在超声挤压过程中,表面粗糙度是评判轴类零件疲劳性能的重要指标,所以研究工艺参数对表面粗糙度的影响以及对工艺参数的优化,对于提高零件的疲劳特性具有重大作用。

近年来,一些国内外学者对超声挤压进行了大量研究。Liu Y等[5]通过建立超声波挤压有限元仿真模型来预测工艺参数与表面性能的关系,研究发现静压的影响远大于振幅的影响。主轴转速越高,应力和应变越小。Wang X等[6]通过对比轧制和超声轧制EA4T车轴钢表面发现,高频振动的作用可以增强疲劳性能。Yao C等[7]对718镍合金车削超声挤压进行研究发现,表面粗糙度Ra的平均值约为0.2 μm,轴向残余应力约为-1 800 MPa,其影响深度增加了近10倍。胡世军等[8]研制新型加工系统进行超声挤压加工,结果发现振动挤压加工后的工件表面光整,对工件表面质量有明显提高。王排岗[9]等采用仿真和实验结合验证的方式,获得最优的超声滚挤压工艺参数,并发现表面硬度随转速和进给速度的提高先增加后下降,随着振幅和静压力的增大而增大。姚国林等[10]以实验数据为基础建立预测模型探究加工参数对力学性能的影响规律。刘鑫[11]通过数值模拟及试验验证相结合的方法研究发现,在较大的振幅和静压力下,表面粗糙度随工件速度和进给速度的增加而增加,随振幅和静压力的增加而减小。曹丽茹等[12]为提高金属材料表层性能进行了正交试验,通过建立表层性能的预测模型,采用遗传算法进行多目标优化,得出最优加工参数域。张明等[13]采用单因素试验法对试件进行超声抛光,研究发现超声抛光后试件的表面粗糙度能达到0.07 μm。

此外,众多学者运用响应曲面法对零件表面质量进行了优化。响应曲面法是利用已知的多项式函数来拟合影响因素与响应值之间的隐式函数[14]。纪道航等[15]利用响应曲面法建立二阶回归模型,并采用遗传算法进行多目标优化,验证了模型的准确性。石文天等[16]通过对硬铝合金铣削试验,分析了工艺参数对表面粗糙度的影响,建立了预测模型并进行了显著性检验。周文昌等[17]通过响应曲面法以最小表面粗糙度为响应优化目标,得到底齿加工的最优参数组合。徐红玉等[18]通过构建改进的响应曲面-满意度函数模型对模型进行优化得到了最优工艺参数组合。

综上所述,众多国内外研究学者对超声挤压加工进行了大量研究,然而利用响应曲面法对超声挤压进行进一步研究预测的较少。因此本文以45钢为研究对象进行超声挤压试验,以主轴转速、进给速度、振幅、静挤压量为主要工艺参数,以表面粗糙度为响应优化目标,探讨工艺参数对表面性能的影响以及最佳工艺参数组合,实现对表面性能的优化控制,为零件投入实际加工应用提供依据。

2 轴类零件超声挤压加工试验

2.1 超声挤压加工试验样件

试验材料选用强度高的45钢棒料,并将其车削加工成长200 mm、直径70 mm的圆柱体样件。其化学成分见表1。

表1 45钢化学成分(质量分数) (%)

2.2 超声挤压加工试验原理

超声挤压技术是一种无切屑的表面光整技术,其原理是220 V的交流电经过超声电源得到高频电压,换能器将高频电压转换成超声振动,超声振动经过变幅杆放大传递给工具头,工具头以正弦形式不断的冲击工件表面,使工件表面微观形貌上的“高峰”受压流向“低谷”,在微观上其“凹凸”互补使得工件表面的粗糙度得到改善,提高表面光洁度。超声挤压加工如图1所示。

图1 超声振动挤压加工示意图

2.3 超声挤压加工试验方案

本试验采用单因素工艺参数变量控制研究机床主轴不同的转速、工具头不同的进给速度、静挤压量以及振幅对零件表面粗糙度的影响规律。具体的试验因素水平见表2。

表2 试验因素水平表

3 单因素结果分析

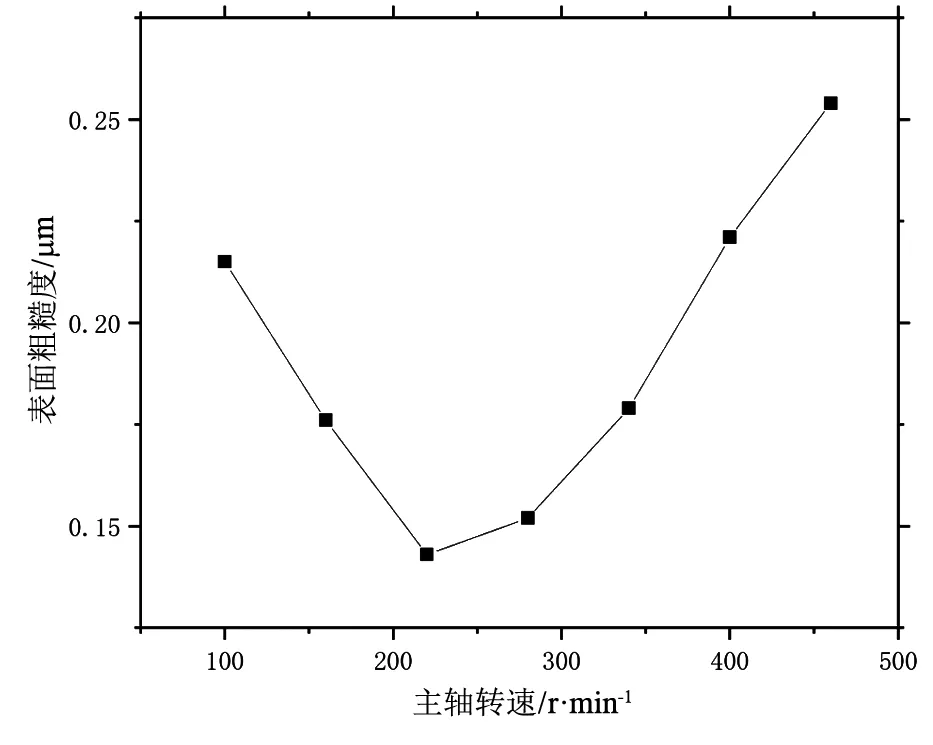
a)主轴转速对表面粗糙度的影响

4 响应面试验结果与分析

4.1 响应面试验设计

在单因素试验的基础上,进一步研究各因素耦合作用对表面粗糙度Ra的影响,采用响应面分析法优化最佳组合工艺。基于Box-Behnken试验设计,选择4个主要因素:主轴转速n、进给速度f、静挤压量P、振幅A进行4因素3水平响应面分析试验。响应面试验因素水平和结果分别见表3和表4。

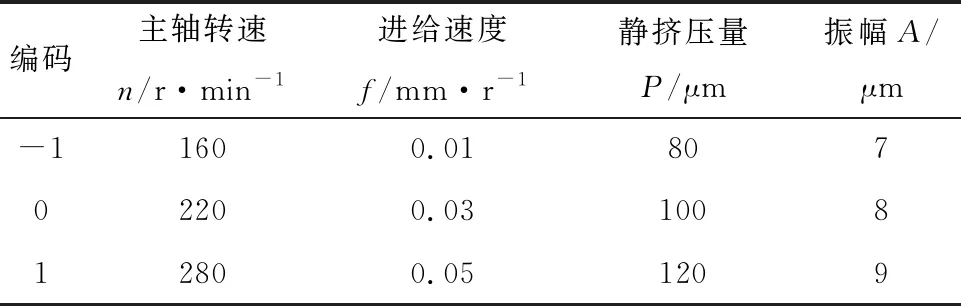
表3 响应面试验因素水平和编码

表4 试验设计与结果

4.2 响应面试验结果及方差分析

利用Design-Expert软件分析试验数据,得到二次多项回归方程:

Ra=1.437 67-0.001 376 57n-2.931 67f-0.011 364 6P-0.141 808A+0.002 916 67nf+2.083 33e-6nP-0.000 179 167nA-0.000 625fP-0.062 5fA-0.000 187 5PA+5.849 54e-6n2+46.708 3f2+6.170 83e-5P2+0.012 308 3A2

(1)

对回归方程进行方差分析(见表5)。其中,F值可以用来检验变量对响应值影响的显著性。F值越大,对应变量的显著性就越高[19]。由表5可知,工艺参数对表面粗糙度Ra影响大小顺序为:振幅A>主轴转速n>静挤压量P>进给速度f。利用Design-Expert软件得到R2为0.989 7,说明此试验模型与实际数据非常一致,模型具有较高的显著性,这使得该模型能够用于分析和预测表面粗糙度Ra的最优工艺。

残差表示实际值和预测值之间的差值。表面粗糙度Ra残差正态分布如图3所示。其分布近似一条直线,表明模型拟合效果较好。因此,验证了建立的表面粗糙度模型的有效性和准确性。

图3 加工模型残差正态分布

4.3 响应面分析

各因素之间的交互作用对表面粗糙度影响的响应面图如图4～图9所示。因素之间相互作用的显著性可以从等高线图上的椭圆形状看出,椭圆形状越明显表示交互作用越显著,如果出现圆形则交互作用不显著;响应面图的坡度越陡峭,说明因素对响应值的影响越大。

图4 主轴转速n和进给速度f的交互作用对表面粗糙度Ra的影响

由图4可知,主轴转速n与进给速度f交互作用对表面粗糙度Ra的影响趋势呈开口向上的抛物曲面分布。表面粗糙度Ra随主轴转速n和进给速度f的增加呈先减后增变化趋势。相较而言,曲面在主轴转速n方向变化幅度较大,表明主轴转速n对表面粗糙度Ra的影响比进给速度f影响大。取主轴转速n为190～250 r/min、进给速度f为0.02～0.04 mm/r水平时,可显著改善产物表面粗糙度Ra。

由图5可知,主轴转速n和静挤压量P交互作用对表面粗糙度Ra影响不显著。表面粗糙度Ra随主轴转速n和静挤压量P的增加呈现先减后增变化规律。相较而言,主轴转速n的敏感性更强,对曲面造成大幅度波动。仅考虑二者影响下的表面粗糙度Ra优化工艺条件集中于主轴转速n为190～250 r/min,静挤压量P为90～110 μm水平区间组合。

根据分泌物的种类，在器官中常见的有粘液腺和浆液腺。粘液腺的分泌物为粘液，它的腺细胞的核扁而小，位于细胞的底部。杯状细胞是单个的粘液腺细胞。浆液腺分泌的是浆液，如同血清样的液体，其腺细胞的核成球形，较大，位于细胞中央(如图2)。除此之外，外分泌腺还有分泌乳汁的乳腺和分泌汗液的汗腺。

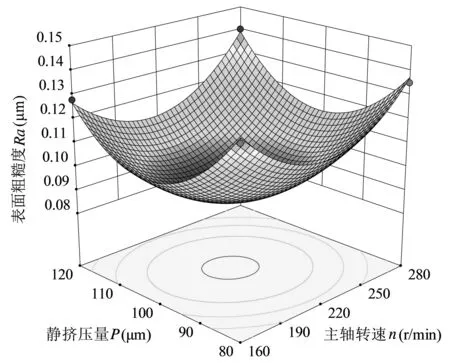
图5 主轴转速n和静挤压量P的交互作用对表面粗糙度Ra的影响

如图6所示,表面粗糙度Ra随主轴转速n和振幅A增加呈先减后增趋势。主轴转速n和振幅A的交互作用对表面粗糙度Ra影响显著。当设置主轴转速n为190～250 r/min、振幅A为7.5～8.5 μm水平范围取值时,为二者交互影响下表面粗糙度Ra的优化处理工艺。

从图7可知,进给速度f和静挤压量P交互作用呈抛物曲面分布,当进给速度f小于0.03 mm/r时,表面粗糙度Ra与进给速度f呈负相关关系;而当进给速度f大于0.03 mm/r时,进给速度f在0.03 mm/r周围取值时为表面粗糙度Ra的最佳工艺参数,同理表面粗糙度Ra随静挤压量P变化的最佳参数为100 μm左右。

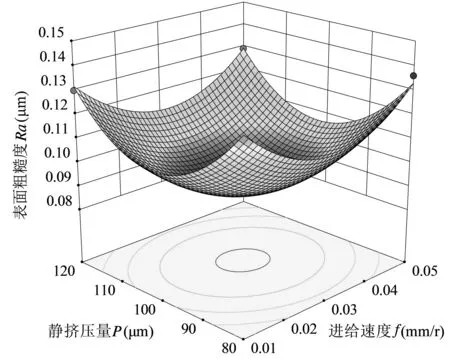
图7 进给速度f和静挤压量P的交互作用对表面粗糙度Ra的影响

如图8所示,表面粗糙度Ra随进给速度f和振幅A的增加而先减后增变化。相较而言,振幅A对表面粗糙度Ra的影响较进给速度f影响显著。取进给速度f为0.02～0.04 mm/r、振幅A为8.0～8.5 μm,有利于减小表面粗糙度Ra水平。

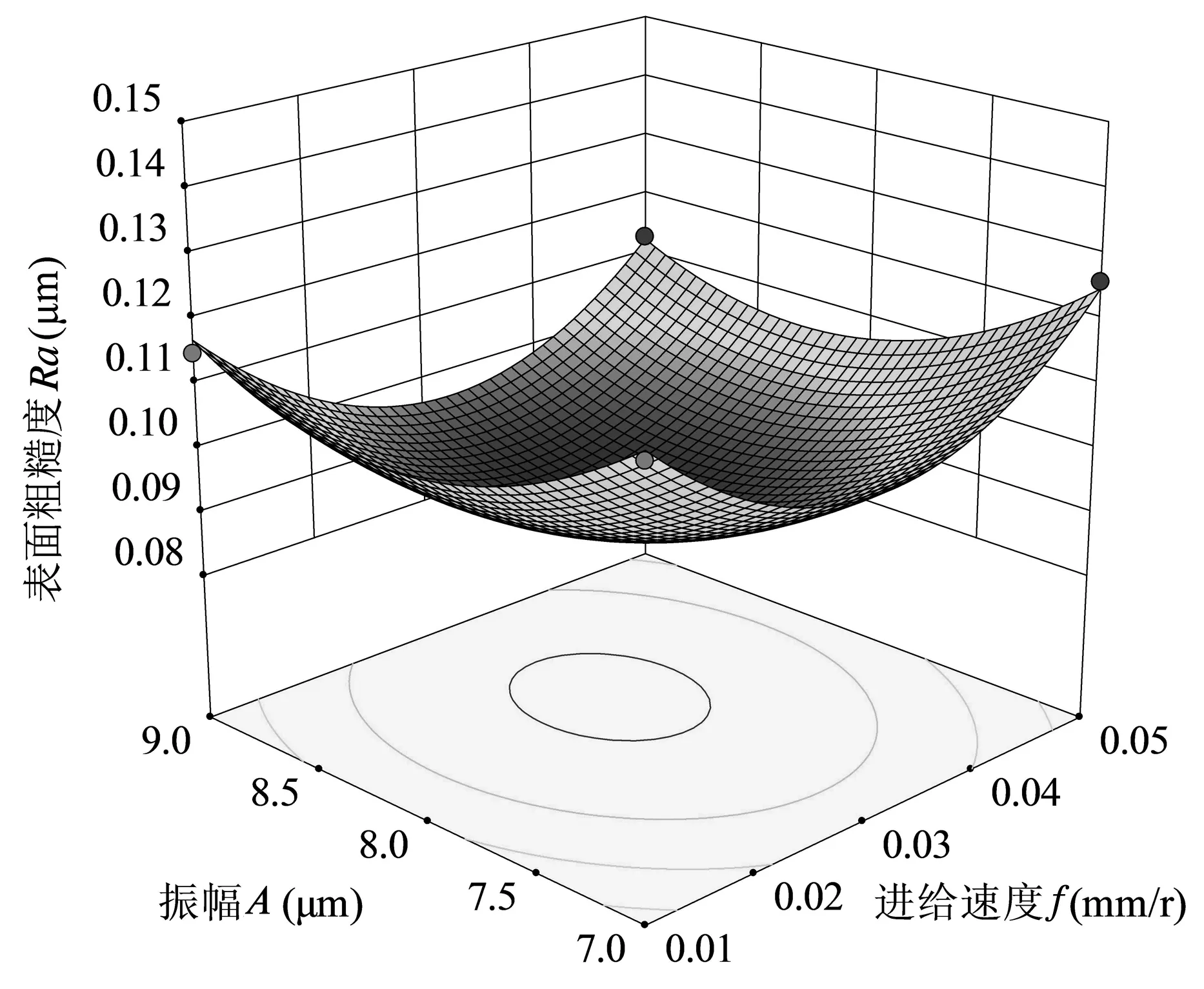
图8 进给速度f和振幅A的交互作用对表面粗糙度Ra的影响

如图9所示,二者交互作用曲面具有较大的纵向跨度且等高线出现椭圆形,表明静挤压量P和振幅A交互作用对表面粗糙度Ra有显著作用。表面粗糙度Ra随静挤压量P和振幅A的增加呈现先减后增趋势,且振幅A对表面粗糙度Ra影响更加显著。取静挤压量P为90～110 μm、振幅A为8.0～8.5 μm水平区间值时,可显著降低表面粗糙度Ra水平。

图9 静挤压量P和振幅A的交互作用对表面粗糙度Ra的影响

为了考虑各因素之间的交互作用对表面粗糙度Ra的影响,基于Design-Expert软件的结果,进一步确定了优化Ra表面最小粗糙度的全局最佳解决方案,表面粗糙度Ra在主轴转速n、进给速度f、静挤压量P、振幅A等因素共同影响下的最优组合工艺如下:主轴转速n为217.48 r/min,进给速度f为0.031 mm/r,静挤压量P为101.013 μm,振幅A为8.192 μm。在此条件下模型预测的表面粗糙度Ra为0.088 μm。

4.4 最优工艺条件试验验证

基于软件预测结果和实际工艺的可行性相结合,取主轴转速n为217 r/min、进给速度f为0.03 mm/r、静挤压量P为101 μm、振幅A为8.2 μm为条件进行3次重复试验,平均表面粗糙度Ra为0.085 μm,与模型预测结果接近。证明了基于该响应面模型的表面粗糙度Ra优化方法的有效性和可行性。

5 结语

本文通过单因素试验和响应曲面法对超声挤压后的轴类零件表面粗糙度进行了研究,得出如下结论。

1)表面粗糙度随着主轴转速、进给速度、静挤压量、振幅的增加呈现先降低后增加的趋势。

2)通过方差分析研究了超声挤压工艺参数对零件表面性能的影响规律,通过软件计算得出各工艺参数对零件表面粗糙度的影响:振幅A>主轴转速n>静挤压量P>进给速度f。

3)在超声挤压加工过程中,振幅对表面粗糙度的影响最为显著。响应曲面法优化得到的最优工艺参数组合如下:主轴转速n为217.48 r/min,进给速度f为0.031 mm/r,静挤压量P为101.013 μm,振幅A为8.192 μm。

4)对最优工艺参数组合进行试验验证,将表面粗糙度的预测结果和试验结果进行对比,相对误差为3.52%,从而证明了优化模型的准确性,可以优化工艺参数,并为实际加工提供理论依据。

5)目前仅对超声挤压后的表面粗糙度进行了影响规律探究,没有对表面特征完整性的变化进行全面的研究。后续可以综合硬度及残余应力等指标探究工艺参数对3个方面的影响规律,并对工艺参数进行全面优化。