基于无差扰动跟踪状态观测器的自抗扰控制技术研究*

石上瑶，刘家豪，石 萱，陈鹏云

（1.中北大学软件学院，太原 030051；2.中北大学机械工程学院，太原 030051；3.浙江财经大学东方学院会计学院，浙江 嘉兴 314408）

0 引言

自抗扰控制（active disturbance rejection controllers，ADRC）是由韩京清教授设计的一种具有总扰动观测并实时补偿的先进设计方法［1］，现在广泛应用于航天航空光电跟踪系统和装甲车辆的火炮跟瞄系统。所谓“自抗扰”，就是要主动从被控对象的输入输出信号中提取总扰动信息——包含系统模型的未知部分和外扰动，然后直接对控制输入信号进行补偿，抵消掉总扰动的作用，从而大大降低扰动对被控量的影响［2-3］。

最近几年，ADRC 技术在工程上的成功应用范例越来越多［4-7］，吸引了理论界越来越多的关注，使其在理论上不断完善。在自抗扰控制理论中，扩张状态观测器（extended state observer，ESO）把系统中的不确定项或者干扰视为系统中的状态之一，建立新的状态空间（也就是扩张空间或者叫增广空间），对这个系统进行观测，从而得到不确定项的估计值［8］，是实现扰动在线估计和补偿的关键。但是现有的ESO 模型有着明显的缺陷，文献［9］提出当存在未知有界扰动时，扩展状态观测器的估计误差不能收敛到零，状态和扰动存在跟踪误差，而这种误差会直接影响闭环系统的控制效果。文献［14］对传统ESO 的理论研究证明了只对常值扰动和低频扰动有好的跟踪性能，但是对高频扰动尤其是谐波扰动跟踪误差大且跟踪相位有较大滞后，造成系统闭环控制精度低。

针对上述问题，为了进一步提高ADRC 的控制性能，本文拟从传统扩张观测器出发，通过对传统扩张观测器动态方程的研究，提出一种无差扰动跟踪ESO（error-free disturbance tracking ESO，EFDTESO），可用于ADRC 控制器。仿真实验表明，基于EFDT-ESO 的ADRC（EFDT-ESO-ADRC）具有跟踪精度高、抗扰能力强、频率稳定性好等优点，对误差扰动具有较强的鲁棒性，可以应用于航天航空和装甲车辆，以提高光电跟踪系统和火炮跟瞄系统的跟踪精度。

1 EFDT-ESO

考察以下一阶线性系统：

其中，x1为系统状态；y 为系统的输出；系统输入u，b系统增益；f 为系统总扰动。

式（1）对应的扩张状态式为：

所以有

考虑到现有的ESO 存在系统扰动跟踪误差，需要本文提出一种无差扰动跟踪状态观测器动态方程为：

由于式（5）中存在对系统输出的微分操作，会放大系统的噪声，所以在设计EFDT-ESO 时，需要忽略微分环节。

由式（6）可以得到如图1 所示的控制框图。

图1 EFDT-ESO-ADRC 控制框图Fig.1 Control block diagram of EFDT-ESO-ADRC

2 EFDT-ESO-ADRC 闭环控制系统

2.1 EFDT-ESO-ADRC

由第1 章分析可知，基于本文提出的EFDTESO，对于一阶不确定系统可以构造一个类PI 控制器，实现无误差跟踪观测扰动。采用的相应状态反馈控制率为：

其中，k1为控制器增益。

那么由式（3）可得到传递函数：

通过化简，可以进一步得到：

由式（2）得到ESO 传递函数：

由状态反馈控制率可以得到其传递函数：

由式（9）可得：

把式（9）与式（12）代入式（11）可得：

其中，

则由式（14）可以得EFDT-ESO-ADRC 的反馈控制率在频域表达式如下：

由此，可以得到基于EFDT-ESO 的ADRC 的闭环控制如图2 所示。

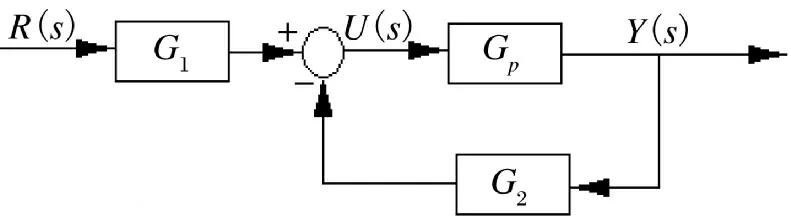
图2 ADRC 闭环控制框图Fig.2 Closed-loop control block diagram of ADRC

基于图2，通过等价变换，可以得到如图3 所示的基于EFDT-ESO 的ADRC 闭环控制原理框图。

图3 基于EFDT-ESO 闭环控制框图Fig.3 Closed-loop control block diagram of EFDT-ESO

基于EFDT-ESO 的ADRC 闭环控制系统的等价单位负反馈开环传递函数：

对图2 进一步移位变换，可以得到EFDT-ESOADRC 的闭环控制框图，如图4 所示。

图4 基于EFDT-ESO 的ADRC 闭环控制框图Fig.4 ADRC closed-loop control block diagram based on EFDT-ESO

2.2 EFDT-ESO 稳定性分析

对于一阶系统的EFDT-ESO 而言，由式（2）和式（6）很容易可以得到下式：

因此，其传递函数为：

由式（6）可得如下传递函数：

因此，由式（19）和式（20）可以得到：

把式（9）带入式（21）可得：

因此，可得：

因此，本文提出的EFDT-ESO 满足稳定性条件。

其中，Ed是传统ESO 的扰动估计的误差ed的拉氏变换；F 是一阶系统扰动f 的拉氏变换；是传统ESO 的扰动估计的拉氏变换。

因此，传统ESO 对于常值扰动有较好的跟踪效果，对于低频扰动有较小的跟踪误差，但是对于高频等其他扰动跟踪误差较大，所以传统ESO 只适合于常值或低频扰动系统。

由本节推导的式（24）可知，本文提出的EFDTESO 不但对常值、低频扰动有很强跟踪能力，而且对于高频扰动也具有很好的跟踪效果。

3 仿真与结果分析

3.1 EFDT-ESO-ADRC 频率分析与仿真

对于ADRC 系统，由于其控制的复杂性，对其进行频率分析比较少，现有文献只是采用简化近似的方法推导其闭环控制传递函数［11-12］，或者在假设的条件下得到控制系统的近似等价单位负反馈开环传递函数，再通过Bode 图［13］，得到相位稳定裕度和穿越频率。

本节将基于上节推导出的EFDT-ESO-ADRC等价单位负反馈开环传递函数，并通过仿真得到系统的相位裕度、幅值裕度和穿越频率等稳定指标进行频率分析。

在频率稳定性仿真中，观测器参数和状态反馈控制参数采用极点重根的选取原则，则有：

那么可得：

系统的传递函数为：

最后可得基于EFDT-ESO-ADRC 的闭环系统等价单位负反馈开环传递函数为：

表1 给出了基于不同系统参数和控制参数的ADRC 闭环控制系统，分别研究系统和控制参数变化时，ADRC 闭环系统的频率特性，对幅值裕度、相位裕度和穿越频率等稳定指标进行对比。

表1 一阶系统与控制参数Table 1 First-order system and control parameters

通过MATLAB 编程仿真，图5、图6 分别绘制出C1-1、C1-2、C2-1、C2-2 与B 闭环控制系统的等价单位负反馈开环系统的对比Bode 图。下页表2对比了如下3 种情况的闭环控制系统的稳定指标：

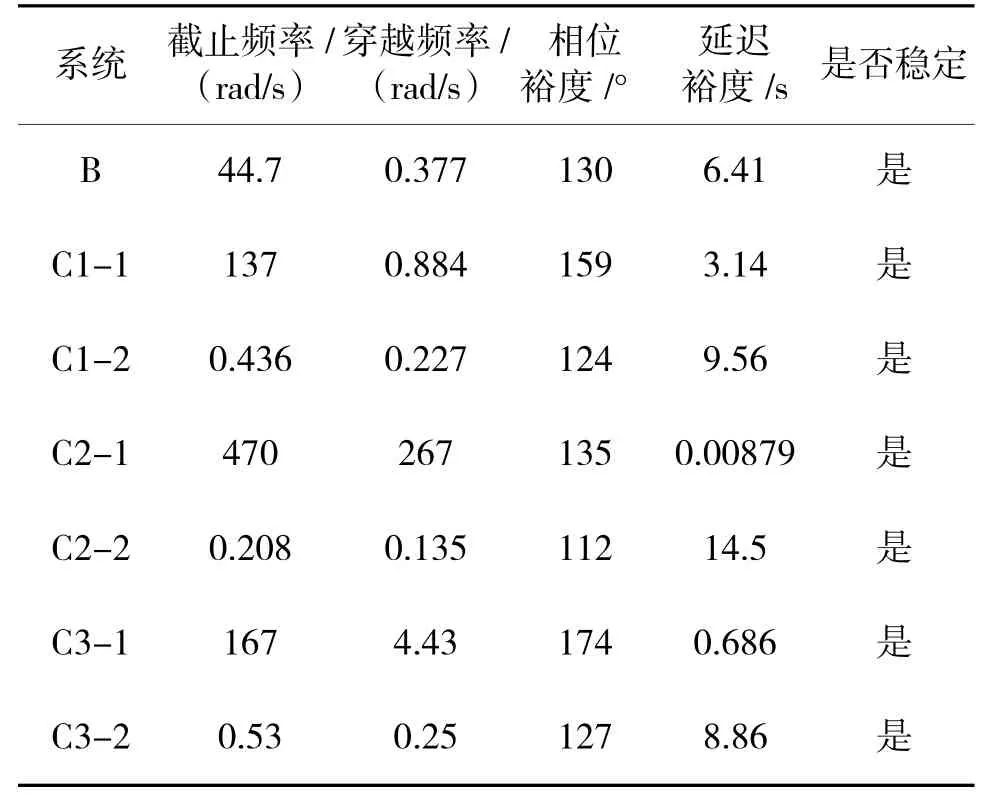
表2 基于表1 的闭环控制系统稳定指标Table 2 Stability indexes of closed-loop control system based on table 1

图5 基于B、C1-1 和C1-2 参数的闭环系统Bode 图Fig.5 Bode diagram of closed-loop system based onB，C1-1 and C1-2 parameters

图6 基于B、C2-1 和C2-2 参数的闭环系统Bode 图Fig.6 Bode diagram of closed-loop system based on B，C2-1 and C2-2 parameters

1）B 与C1-1、C1-2 对比；

2）B 与C2-1、C2-2 对比；

3）B 与C3-1、C3-2 对比。

基于C1-1、C1-2 参数的EFDT-ESO-ADRC 闭环控制系统，只是对参照闭环系统B 的系统增益b作了改变。由图5 和表2 分析可知，在EFDT-ESO 的名义增益不变情况下，系统增益越大，相位裕度越大，穿越频率越高，截止频率越高，而延迟裕度越低。

基于C2-1、C2-2 参数的EFDT-ESO-ADRC 闭环控制系统，只是相对参照系统B 的EFDT-ESO 的观测带宽ωo和控制带宽ωc作了相应修改。由图6和表2 分析可知，随着EFDT-ESO 的观测带宽ωo和控制带宽ωc的增大，相位裕度越大，穿越频率越高，截至频率越高，但延迟裕度越小。

基于C3-1、C3-2 参数的EFDT-ESO-ADRC 闭环控制系统，只是对参照闭环系统B 的系统名义增益作了改变。由图7 和表2 分析可知，在系统增益不变情况下，系统名义增益越大，相位裕度越小，穿越频率越低，截止频率越低，而延迟裕度越大。

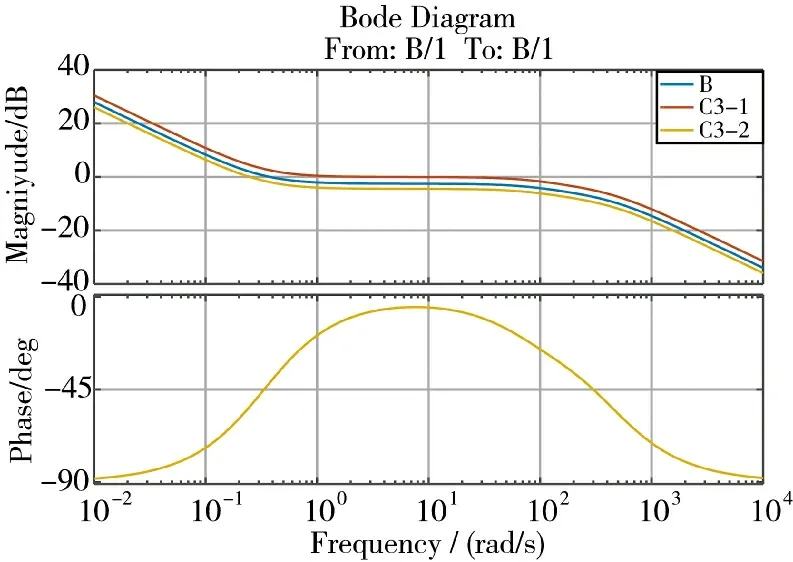
图7 基于B、C3-1 和C3-2 参数的闭环系统Bode 图Fig.7 Bode diagram of closed-loop system based on B，C3-1 and C3-2 parameters

3.2 EFDT-ESO-ADRC 的性能分析与仿真

在无人战车的火炮跟瞄控制系统中，由于路况高低起伏未知，以及传动链的抖动和火炮发射的反冲，使火炮末端存在冲击和振动，即有外界未知谐波扰动，以传统ESO 的闭环系统作为参照标准，同一条件下与EFDT-ESO 的闭环回路系统进行仿真对比，对比仿真使用的传统ESO 模型如下：

观测器参数和状态反馈控制参数采用极点重根的选取原则，则有：

图8 扰动跟踪对比Fig.8 Disturbance tracking comparison

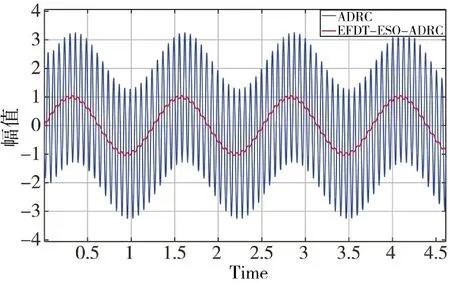
图9 扰动跟踪误差对比Fig.9 Disturbance trackingerror comparison

图10 输入信号与输出信号对比Fig.10 Comparison between input signals and output signals

图11 控制精度对比Fig.11 Control accuracy comparison

由仿真结果可以明显看出，本文提出的EFDT-ESO 不但可以跟踪常值扰动，而且对谐波扰动也具有优良的跟踪能力，相比于传统ESO，显著提高了扰动跟踪性能，特别是面对大幅谐波扰动系统，具有更好的谐波扰动跟踪能力。因此，基于EFDT-ESO 的ADRC 面对谐波扰动时具有更好的抗干扰能力。同时，EFDT-ESO-ADRC 相比于传统ADRC 具有更快的响应速度，可以实现对阶跃信号的快速响应和稳定跟踪；在稳定阶段，EFDT-ESO-ADRC 的输入跟踪精度远高于传统的ADRC，且可快速跟踪扰动信号。因此，相比于传统ADRC，本文提出的EFDT-ESO-ADRC 具有跟踪精度高、抗扰能力强等优点，对谐波扰动具有强的鲁棒性等优势，更适用于有高频谐波扰动的系统，可以显著抑制系统的振动，提高系统的精度和稳定性。

4 结论

针对现有ESO 的不足，本文提出一种可用于ADRC 的EFDT-ESO，并进行了频率与性能分析和控制精度与抗干扰能力仿真。本研究可得到以下结论：

1）EFDT-ESO 相比于传统的ESO 在扰动跟踪以及抗干扰能力方面有显著的优势，尤其是存在谐波扰动的情况下，基于EFDT-ESO 的ADRC 可以有效地消除谐波扰动，显著抑制了系统的振动。

3）被控系统系数EFDT-ESO-ADRC 参数ωo、ωc、在大范围内的改变，并不影响EFDT-ESOADRC 闭环控制的稳定性，充分证明了基于EFDTESO-ADRC 的控制系统具有强鲁棒性。