多层钒矿体开采应力迁移规律和分布研究
池秀文 董浩然 汪宗英 王其洲 赵 龙 范纯超
(1.矿物资源加工与环境湖北省重点实验室,湖北 武汉 430070;2.武汉理工大学资源与环境工程学院,湖北 武汉 430070;3.山东黄金矿业股份有限公司,山东 济南 250100)
钒元素因其优异的物理和化学特性,在提高金属材料物理力学性能、改善非金属材料的化学性质以及作为蓄电池材料等方面得到了广泛应用。但钒矿资源复杂的赋存条件和针对这类赋存条件不成熟的开采技术导致我国钒矿生产能力小,安全性也较差。钒矿资源多赋存于含钒沉积页岩中,常以缓倾斜—倾斜、薄—中厚矿体产出,一般为多层排列分布,是一种典型的多层矿体,并且各矿层的埋深、走向、厚度和品位变化大[1]。开采近距离的多层矿体时,由于矿体层间距离较小,相邻矿层开采的相互影响显著,采场围岩结构和多次扰动后的次生应力场变化剧烈,导致相邻待采矿体的开采环境趋向复杂,形成了多层矿体开采时特殊的地压环境,增加了开采难度。
针对上述问题,许多学者在开采顺序、开采方向等方面开展了深入研究,如叶义成等[2]通过相似模拟试验,分析了不同开采顺序多层矿采空区围岩的变形规律,得出多层矿适合采用前进式开采方式。谈晓明等[3]经过现场研究,对某多层矿体矿层回采顺序、各矿块的超前关系、矿房布置形式等进行了优化分析。殷亮[4]根据某多层薄矿脉近似水平的分布特点,利用数值模拟得到合理的开采顺序。胡倩等[5]根据不同的围岩移动角、矿层倾角与矿层间距,确定相邻多层矿同阶段开采时的超前距离与回采顺序。池秀文等[6-7]基于弹性梁和薄板模型,求解了多层矿顶板的应力分量表达式,得到顶板的极限跨距和破断距。在采用相似模拟、数值模拟和现场试验等方法分析多层矿开采稳定性时,一般利用模拟或试验的应力和应变结果,判断围岩破坏情况,据此评价开采方案的合理性。此外,不少学者还针对多层矿体的开采方法开展研究并得到了不少有益结论,如林坤峰等[8]提出大盘区机械化分层充填沿倾向后退式开采和盘区房柱法两种多层矿开采方法。古德生等[9]提出了深孔合采井下矿废分离连续采矿法,避免了多层矿间柱回采带来的一系列技术经济难题。孟祥凯等[10]基于某缓倾斜薄—中厚铁矿床矿体储量大、品位低的特点,提出两步中深孔联合采矿法。诸利一等[11]提出了单层浅孔条带式充填采矿法、多层合采条带式充填采矿法和中深孔条带充填采矿法等多层矿开采方法。对于层间距小的多层矿体,解联库等[12]利用综合技术经济比较分析方法,分别研究了合采和分采过程中的合理采矿方法。此外,陈庆发[13-14]提出的协同开采理论也为多层矿开采提供了新思路。综上可知,已有的多层矿围岩稳定性研究,均是基于传统单层矿开采条件做出的拓展,鲜有以多层矿体间开采扰动导致的特殊地压环境为基础条件开展研究。
煤炭资源赋存特征与含钒页岩矿体较为近似,均呈厚度不等的多层状排布,但煤炭资源赋存条件相对简单,已经形成了系统性极强的开采理论和方法。如采用综采放顶煤方式回采时,将开采工作面附近的围岩按应力分布特征分为应力稳定区、应力增高区、应力恢复区和原始应力区,4 个区域随着开采工作面向前推进,根据其不同的应力特征可采取针对性较强的地压管理措施。为此,本研究借鉴煤矿地压分析理论,在多层矿体开采过程对采场围岩进行分区,并探究不同区域的应力迁移特征,为多层状金属矿体开采理论研究与实践提供参考。
1 单层矿应力迁移特征
1.1 采空区围岩应力分布规律
在研究开采过程中的采空区稳定性问题时,常将复杂的地质条件进行简化,以便建立数学模型并分析其应力状态。对于一个处于某种应力状态下的无限弹性各向同性平面,用U0(x,y)表示对应这种应力状态的应力函数,并将无孔平面内的应力状态称为基本应力状态[15-16]。
假如在所研究的平面内作任意形状的孔(图1),那么孔的存在就会引起平面内应力重新分布。新的应力状态可以表示为
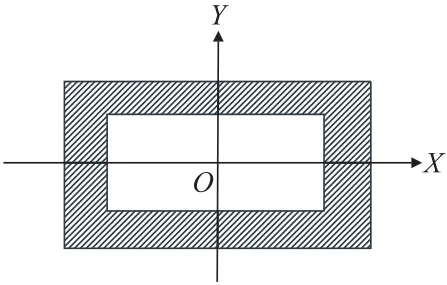
图1 简化的含孔平面Fig.1 Simplified plane with holes
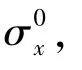
对于基本应力状态和附加应力分量,根据双调和函数可以分别找出两个复变函数的穆斯海里什维里函数φ0(z),ψ0(z)和φ∗(z),ψ∗(z)[17-18]。与新的应力状态(式(1))相对应的函数φ1(z)和ψ1(z)为
式中,z为复数;φ1(z)和ψ1(z)为变化后的应力函数;φ0(z),ψ0(z)为初始应力状态对应的穆斯海里什维里函数;φ∗(z),ψ∗(z)为附加应力状态对应的穆斯海里什维里函数。
当用与OX轴成α角的力p拉伸连续平板时,板的基本应力状态可表示为
式中,σx,σy,τxy为基本应力分量,MPa;p为作用于平板上的力,MPa;α为力与OX轴夹角,(°)。
任一处的应力函数可表示为
式中,U0(x,y)为平板上任一处应力函数表达式;x、y为该处对应的坐标值。
假如在已知平板中作一孔使其中心和XOY坐标系的原点相合,并且其周界不受外力,那么带孔平板的应力函数φ1(z)和ψ1(z)可表示为
式中,i为虚数单位。
当所作孔的形状为矩形、正方形、三角形、梯形等有限部分的平面时,如果能将已知区域映射为一单位圆的函数z=ω(ζ),那么问题就可以用泛函方程组确定边界条件φ(ζ)和ψ(ζ)来解决[19]。z=ω(ζ)见下式:
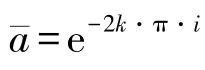
根据模拟需求,仅对α=π/2 的情况进行如下分析计算:
式中,φ(ζ),ψ(ζ)为泛函方程组确定的边界条件;R为矩形孔顶点处的曲率半径。
将式(8)代入式(9),分开实部和虚部,得到应力分量σρ,σθ和τρθ的表达式:
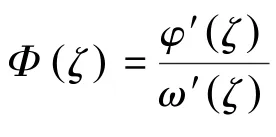
将该情况的矩形孔周界上的σθ被p除得的值列出,结果见表1。
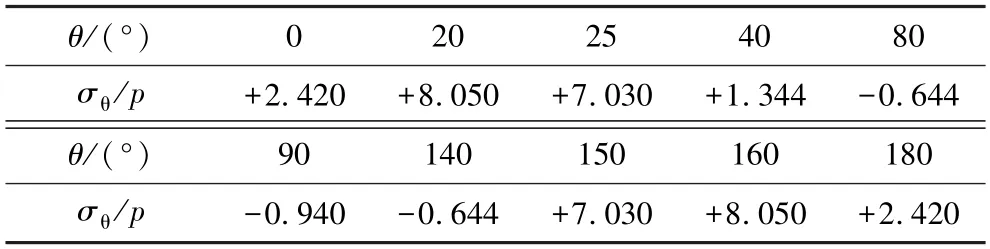
表1 长宽比为5 的条件下α=π/2 时的σθ/p 值Table 1 σθ/p values at α=π/2 for an aspect ratio of 5
对表1 中的数据进行拟合,所得曲线如图2所示。
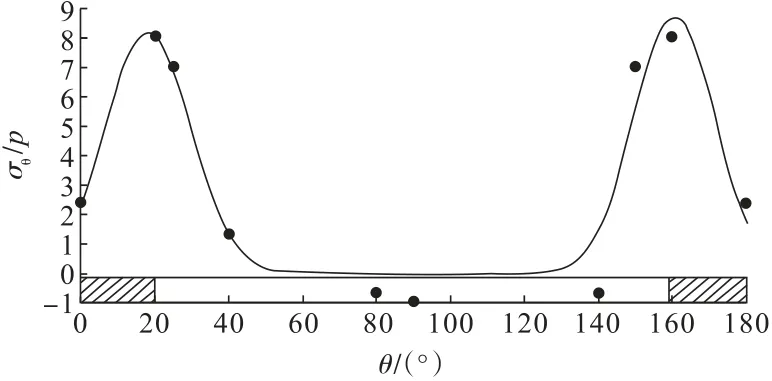
图2 不同角度下的应力变化率拟合曲线Fig.2 Fitting curve of stress change rates at different angles
1.2 单采场应力变化区域划分
根据某含钒页岩多层矿的岩石力学参数建立FLAC3D数值模型(表2),对上述采空区围岩应力分布规律进行验证。该矿体埋深185 m,采场宽度为10 m,以1 m/次的掘进速度推进,分别得到5、10、15、20、25 m采空区顶板围岩的垂直应力分布曲线(拉应力为正值、压应力为负值),如图3所示,0 m 为初始开采位置。采空区形成后,顶板产生变形,应力得到释放,顶板围岩的垂直应力迅速跌落至稳定值。开采工作面附近的围岩承受采空区上覆岩体向周围岩体转移的荷载,此时,垂直应力向远离工作面的方向迅速增加至峰值,应力峰值随着开采宽度增加而增高,一段距离后应力逐渐降低至原岩应力。根据图3所示的应力迁移规律,可将采场围岩划分为如图4所示的应力释放区、应力跌落区、应力增高区和原始应力区,垂直应力的变化率分布与图2 拟合曲线基本符合。
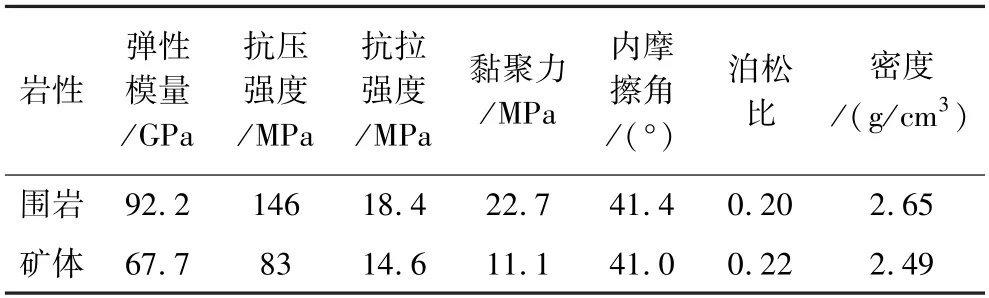
表2 岩石力学参数Table 2 Rock mechanical parameter
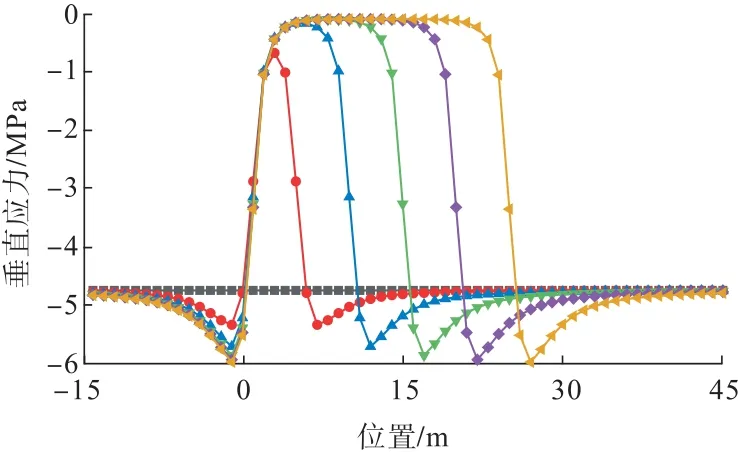
图3 不同开采进度矿体上部围岩垂直应力分布曲线Fig.3 Vertical stress distribution curves of the upper surrounding rock of orebody with different mining progress
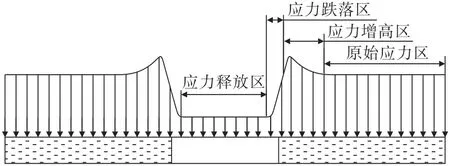
图4 单采场应力变化分区Fig.4 Stress variation zones of single stope
应力释放区和应力增高区对单采场的稳定性影响较大,目前主要的研究集中于这两个分区,即采空区的顶板、侧壁和矿柱。应力释放区对应采场的顶板位置,该区域围岩下部临空面受拉应力作用,极易产生冒落甚至垮塌。应力增高区对应采场侧壁或矿柱位置,该区域承受高于原岩应力的荷载,提高了围岩破坏的风险,若此时能量积聚较高且瞬时释放,极易产生岩爆。
1.3 单采场应力增高区应力分布特征
针对单采场,根据式(10)计算不同开采过程中的围岩垂直应力变化率α:
式中,α为围岩垂直应力变化率;σi为距开采起点im处的当前垂直应力,MPa;σ0为初始垂直应力,MPa。
如图5所示,将α>0.1 的区域划分为高应力增加区,0.01<α<0.1 的区域划分为低应力增加区,并在图中标记出应力峰值区。根据图5 可知,开采5 m 后出现高应力增加区,随着开采的推进,高应力增加区最终稳定在距离开采工作面5 m 内,低应力增加区范围稳定在距离开采工作面5~19 m,应力增高区峰值出现在距离开采工作面2 m 处。
不同跨度采空区对应的应力增高区应力峰值不同,采空区跨度越大,峰值越高。利用上述结果拟合得到的峰值应力变化率表达式为
式中,Lc为采空区跨度,m;R2为拟合优度。
选取不同跨度的采空区,分析了应力增高区的应力变化率随距离的变化特征如图6所示。由图6 可知:当采空区宽度为5~24 m 时,在应力峰值区以外的区域,应力变化率满足式(12),其中a1=0.129~0.217,a2=-0.240~-0.201。
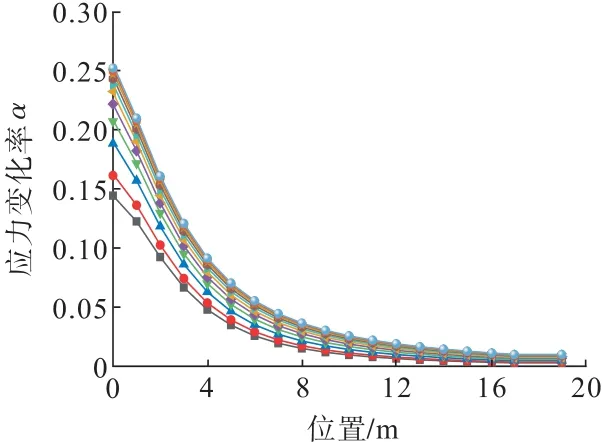
图6 应力增高区应力变化率随距离变化曲线Fig.6 Variation curves of stress change rate with distance in the area of increased stress area
式中,L为与应力峰值点距离,m;a1、a2为常数。
1.4 单采场应力跌落区应力分布特征
应力跌落区是应力增高区与应力释放区的过渡区域,不同宽度采空区的应力变化率随着应力增高区峰值点距离的变化曲线如图7所示。
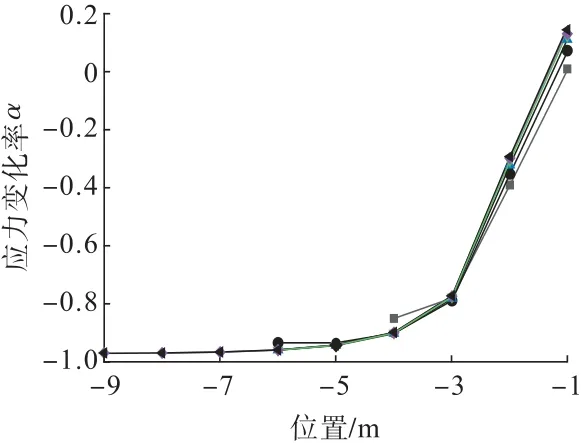
图7 应力跌落区应力变化率随距离变化曲线Fig.7 Variation curves of stress change rate with distance in attenuated stress area
图7所示曲线可用如下三次函数式进行表示:
式中,b0,b1,b2,b3分别为拟合曲线三次函数式的常数系数。
当采空区尺寸为24 m 时,应力跌落区的应力变化率随峰值点距离的关系可表示为
1.5 多采场应力增高区应力变化率叠加特征
煤层工作面开采时,放顶工作使应力释放区顶板围岩下落充填采空区,最终实现该区域内的应力稳定。因此,煤矿开采中将此区域称为应力稳定区,使用崩落法开采层状金属或非金属矿与之类似。使用充填法开采时,充填体代替崩落的废石起到支承采空区顶板的作用,同样能达到类似效果。在围岩稳固的情况下使用空场法开采,采空区顶板能够依靠自身强度承受一定的荷载,但随开采跨度增加,顶板中部所受拉力逐渐增大,考虑到岩体本身软弱结构面的存在,应力释放区的宽度不宜过大。除了利用充填等措施外,工程中会优化采场参数,控制采空区跨度,从而将应力释放区限制在合理宽度,具体方法是间隔一定距离留设矿柱。通过上文分析可知,采空区的应力增高区必定位于矿柱中,两个相邻采空区的应力增高区若在矿柱内重叠,则进一步增加了矿柱荷载,增大了矿柱失稳风险(图8)。
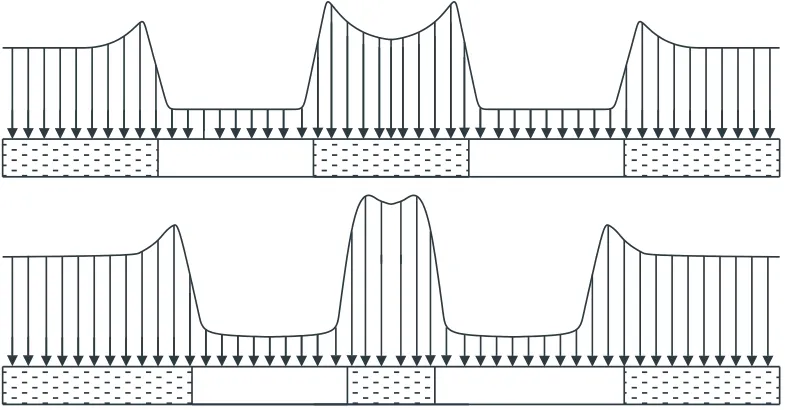
图8 不同宽度矿柱应力叠加特征示意Fig.8 Schematic of stress superposition characteristics of pillars with different widths
如图9所示,设两个跨度分别为20 m 和10 m 的采空区之间留设10 m 宽矿柱,模拟单独开采10 m、单独开采20 m 和两者全部开采3 种工况,分别得到如图10所示的采空区围岩应力变化率曲线。将两个采空区单独作用值相加,发现其与两个采空区共同作用的模拟值一致,可以认为矿柱内部应力增高区的应力变化规律由两侧采空区围岩应力代数叠加得到。当采空区数目增加时,矿柱内部应力增高区的应力变化规律同样满足上述规律。

图9 20 m 采空区-10 m 矿柱-10 m 采空区示意Fig.9 Schematic of 20 m goaf -10 m pillar -10 m goaf
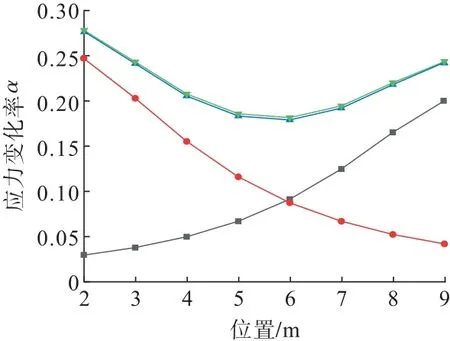
图10 应力增高区应力变化率模拟值随距离变化曲线Fig.10 Curves of simulated stress change rate with distance in increased stress area
选取图9所示的20 m 采空区-10 m 矿柱-10 m采空区的模型,利用式(12)求得3 种工况下的应力变化率。如图11所示,两个采空区共同作用的应力计算值与模拟值的变化规律基本一致。在对矿柱进行理论分析时,通常将其视为受均布荷载,然而通过上述分析可知,矿柱受到的荷载大小和规律应由两侧采空区共同决定。
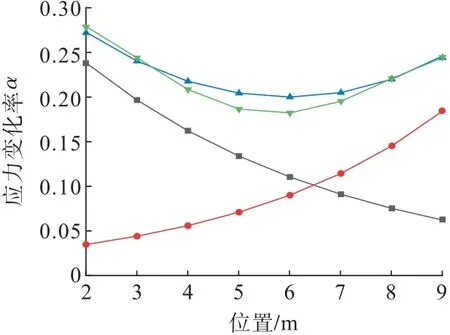
图11 应力增高区应力变化率计算值随距离变化曲线Fig.11 Curves of calculated stress change rate with distance in increased stress area
2 双层矿体应力迁移规律
2.1 水平位置关系对矿岩应力迁移特征的影响
研究双层矿体开采应力迁移规律时,需要考虑两层矿体的位置关系,按矿体的重叠关系与长度,可分为上覆型完全重叠、下悬型完全重叠、部分重叠和不重叠4 种类型。其物理含义可表述为:上覆型完全重叠的双层矿,上层矿体长度大于下层矿体,且下层矿体完全与上层重叠;下悬型完全重叠的双层矿,下层矿体长度大于上层矿体,且上层矿体完全与下层重叠;部分重叠的双层矿,仅有部分区域重叠;不重叠的双层矿,完全不存在重叠区域。由于矿体间距过大,层间应力扰动不明显,因此为便于观察,建立若干组不同重叠关系的近距离矿体数值模型用于分析其应力扰动特征,矿体间距设置为8 m。
如图12(a)所示,建立上覆型完全重叠的双层矿数值模型,自上而下分别留设50、20 m 采空区,先回采上层矿体,再回采下层,分析夹层应力分布规律。分别单独开采上下两层矿体时,满足应力释放区、应力跌落区、应力增高区和原始应力区4 个应力变化区域划分(图12(b))。两层矿体全部开采后,应力扰动叠加。下层采空区的4 个应力变化区完全位于上层采空区的应力释放区下方,此时上层采空区的应力释放区可视为下层采空区的次生原始应力区,在此基础上形成次生应力释放区、跌落区和增高区。根据图12(c)最小主应力曲线可知,夹层最大压应力在上层采空区的应力增高区达到最大值,下层采空区的应力增高区与上层采空区的应力释放区的重叠区域也出现较小的峰值。由图12(d)最大主应力分布曲线可知,拉应力在两层采空区的应力释放区重叠处最大。
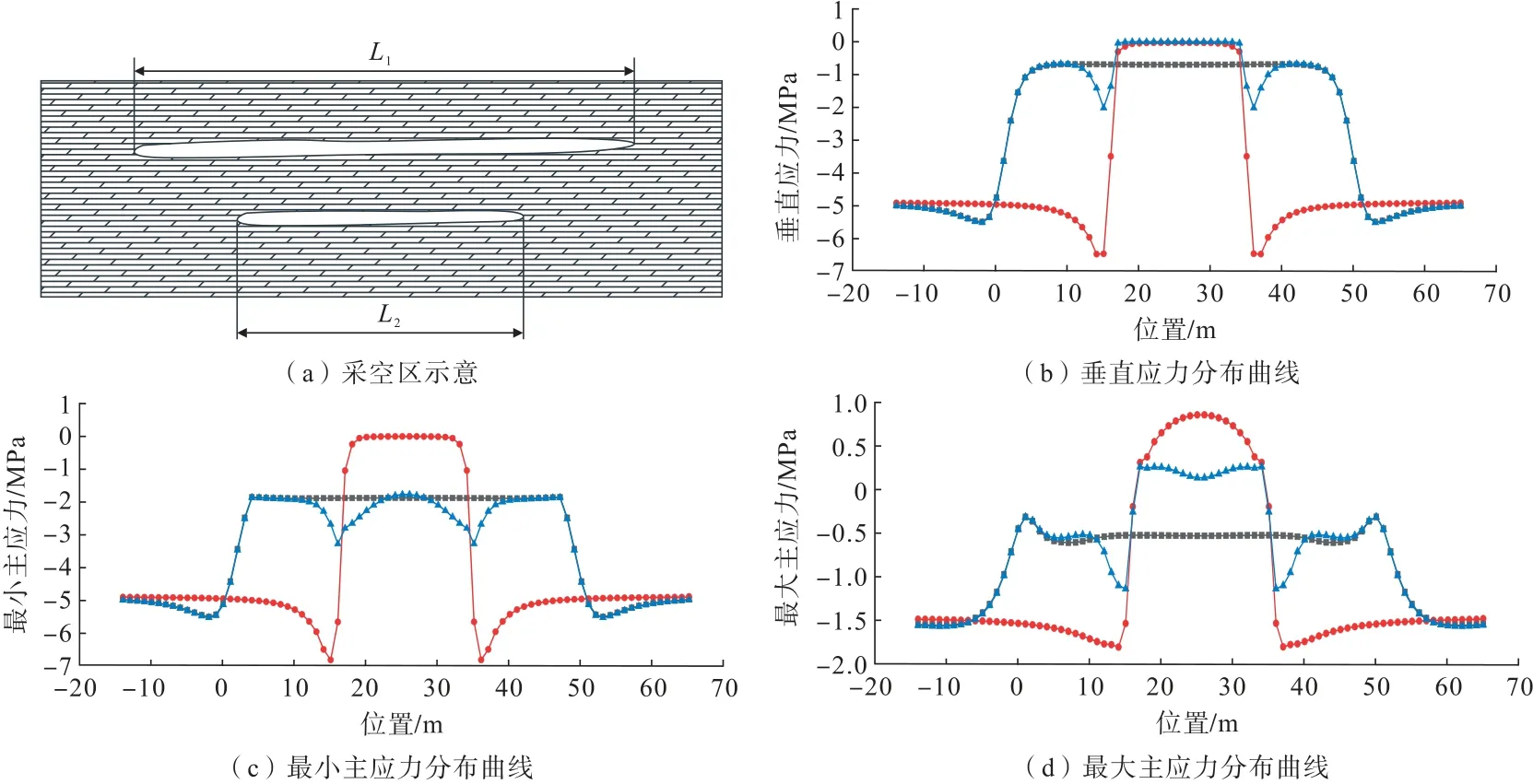
图12 上覆型完全重叠双层矿体Fig.12 Overlying type completely overlapped double-layer orebody
本研究构建的下悬型完全重叠的双层矿数值模型如图13(a)所示。模型自上而下开采分别留设的20、50 m 采空区。夹层的垂直应力扰动主要受下层采空区控制,最大压应力出现在下层采空区的应力增高区,上层采空区的应力增高区与下层采空区的应力释放区重叠处的拉应力最大。

图13 下悬型完全重叠双层矿体Fig.13 Overhanging type completely overlapped double-layer orebody
如图14所示,对于部分重叠的双层矿,自上而下开采,左侧非重叠区的应力扰动受下层采空区控制,右侧非重叠区的应力扰动受上层采空区控制,重叠区域则因两层采空区的扰动叠加产生变化。最大压应力出现在下层采空区非重叠区域的应力增高区,最大拉应力出现在下层采空区的应力释放区与上层采空区的应力增高区重叠处。
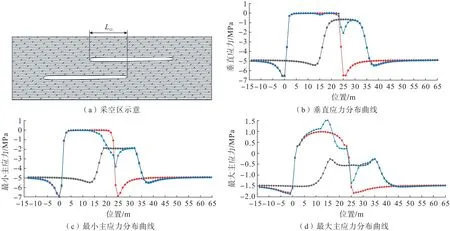
图14 部分重叠双层矿体Fig.14 Partially overlapped double-layer orebody
当由上至下依次开采形成两层不重叠的采空区时,若距离足够远,则应力扰动区域互不影响;若距离小于任一采空区的应力增高区扰动范围,则会出现应力增高区叠加。如图15所示,最大垂直应力和最大压应力均出现在两层采空区的应力增高区重叠部位,最大拉应力处于下层采空区的应力释放区中部。
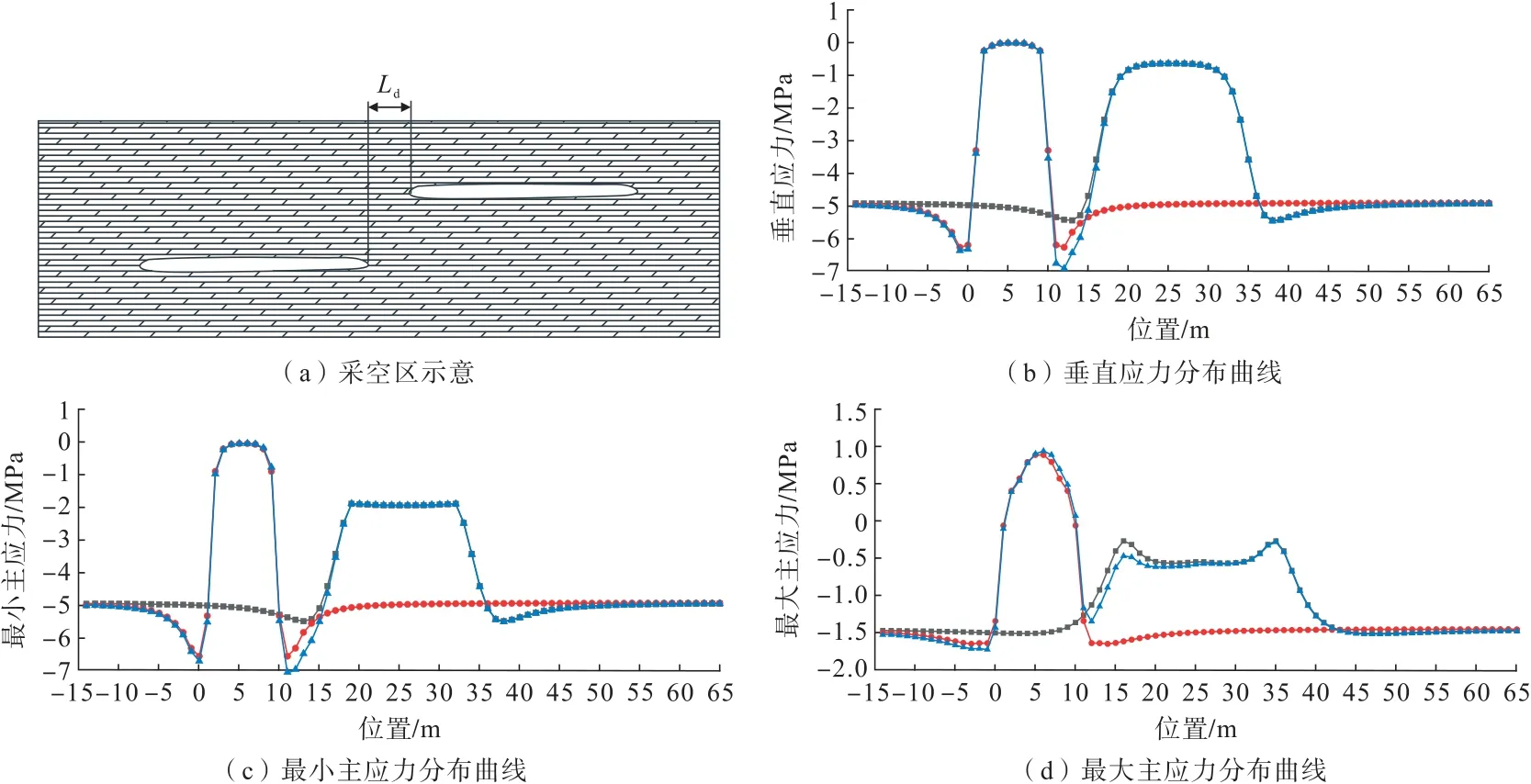
图15 不重叠双层矿体Fig.15 Non-overlapped double-layer orebody
上述4 种重叠关系中,下层采空区顶板受到的拉应力较大,尤其当下层采空区的应力释放区与上层采空区的应力增高区重叠时,拉应力最大;最大压应力位于较大跨距采空区的应力增高区,当上下两层采空区的应力增高区重叠时,重叠处的压应力进一步增加。
2.2 垂直距离对矿岩应力迁移规律的影响
双层矿体的相互扰动程度和范围受矿体间距影响,矿体间距足够大时,相邻矿层不会形成开采扰动。因此,有必要研究矿层间距对开采扰动的影响,确定不同矿层间距的应力扰动特征。在分析不同采空区长度的垂直应力变化率后,设置采空区长度为24 m,模拟得到采空区下方1,3,6,11,16,21 m 垂直应力变化率分布曲线(图16)。上层矿体的开采扰动随着深度增加而逐渐降低,应力增高区在采空区以下6 m 位置几乎完全消失。应力跌落区的应力跌落速率逐渐放缓。应力释放区的影响范围较大,采空区下方21 m处应力扰动依然存在,但已经回落至较小值。因此,可按应力增高区和应力释放区的扰动范围,将应力扰动区域划分为强扰动区、弱扰动区和无扰动区,3 个区域分界线为强扰动距和弱扰动距。矿体间距小于强扰动距时,应力增高区和应力释放区共同对相邻矿层造成扰动,形成强扰动区;矿体间距大于强扰动距且小于弱扰动距时,应力释放区对相邻矿层造成扰动,应力增高区不造成扰动,形成弱扰动区;矿体间距大于弱扰动距时,应力增高区和释放区对相邻矿体均不造成扰动,此处成为无扰动区。综合上述数值模拟结果得到该模型中强扰动距为6 m,弱扰动距为22 m。
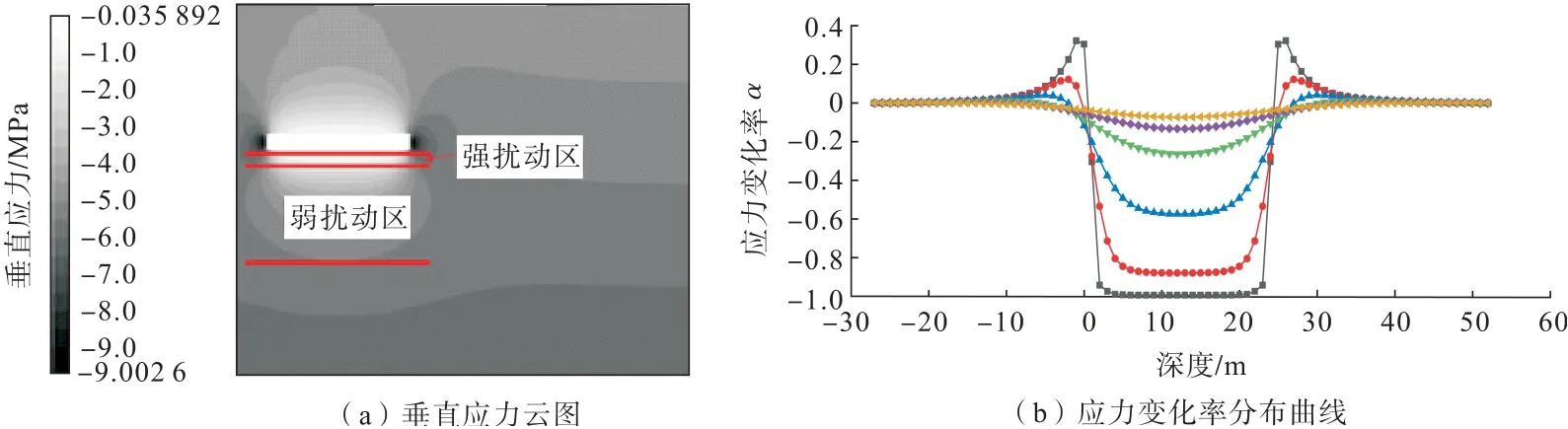
图16 单层采空区对下部岩体扰动分布Fig.16 Distribution of disturbance caused by single goaf to lower rock mass
以不完全重叠的双层矿体为例,根据24 m 采空区的应力扰动区分布情况设置3 组数值模型,矿层间距为3,15,25 m。如图17所示,矿层间距为3 m 时,下层采空区位于上层采空区的强扰动区,受上层采空区应力增高区和应力释放区共同影响。如图17(c)和图17(d)所示,上层采空区的应力释放区导致下层采空区右侧压应力和拉应力降低,上层采空区的应力增高区导致下层采空区右侧壁出现小型压应力峰值,中部拉应力有较大幅度增加。
如图18所示,矿层间距为15 m 时,下层采空区位于上层采空区的弱扰动区,受上层采空区应力释放区影响,表现为下层采空区右侧压应力小幅度降低,拉应力小幅度增高,但总体变化值较小(图18(c)和图18(d))。

图18 夹层为15 m 的应力扰动情况Fig.18 Stress disturbance of a 15 m interlayer
如图19所示,矿层间距为25 m 时,下层采空区位于上层采空区的无扰动区,单独开采下层矿体与开采双层矿体时的应力变化几乎相同,可认为上层采空区未对下层矿体开采造成影响。
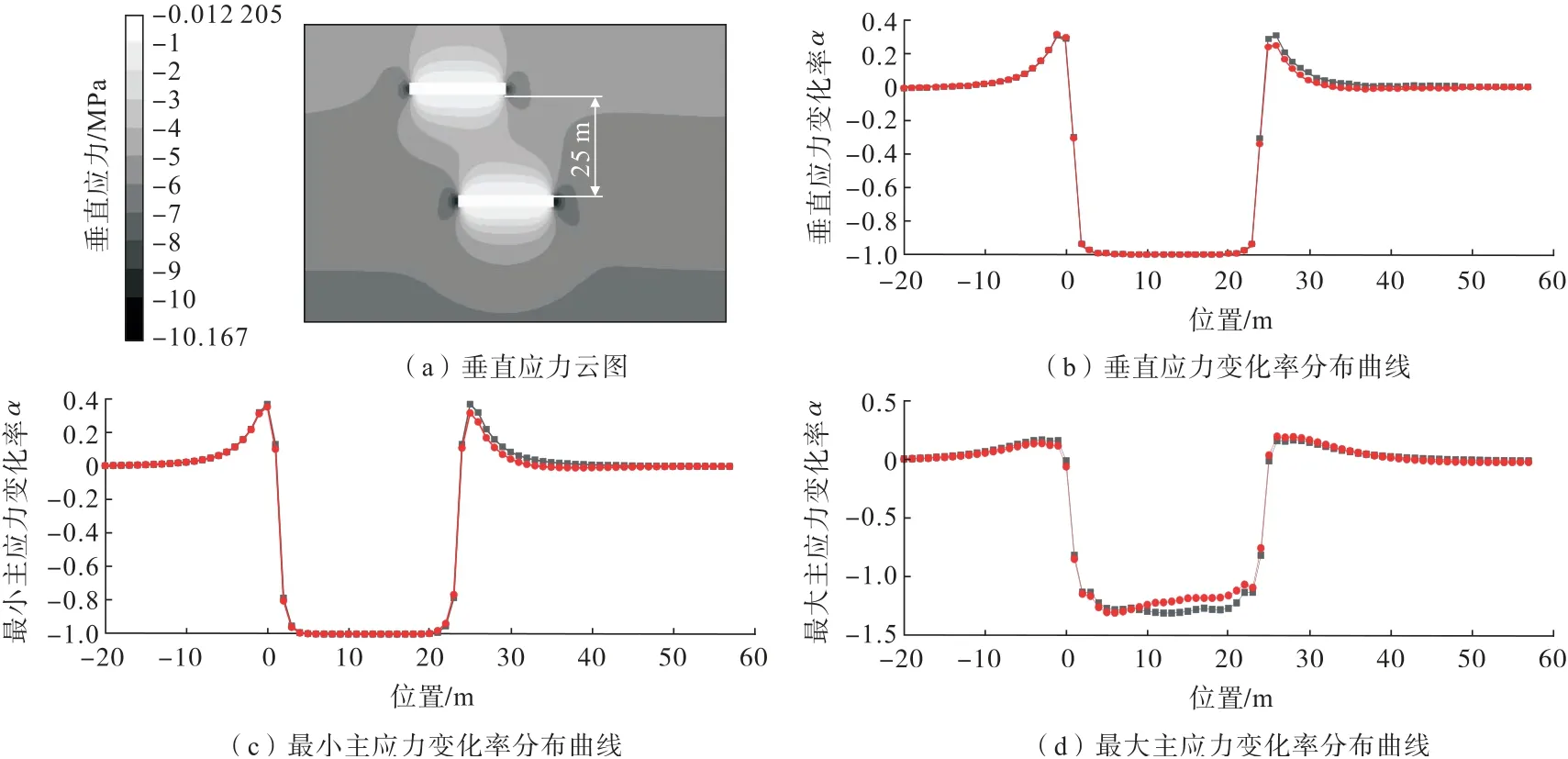
图19 夹层为25 m 的应力扰动情况Fig.19 Stress disturbance of a 25 m interlayer
3 结论
(1)根据含钒矿体开采后的垂直应力变化规律,将采空区围岩划分为应力释放区、应力跌落区、应力增高区和原始应力区等4 个区域。
(2)单采场采空区跨度与其围岩应力峰值为正相关关系,即采空区跨度越大,其应力峰值越高,并且应力增高区以深围岩内的应力变化率随着与应力峰值点距离的增大呈幂函数关系减小,应力跌落区内的应力变化率随着与应力峰值点距离的增大而增大;相邻采空区的应力增高区会在两者间的矿柱内叠加,矿柱内某点的应力变化率为两侧采空区分别在该点引起的应力变化率之和。
(3)双层矿双采场开采后,当下层采空区应力释放区与上层采空区应力增高区重叠时导致围岩内拉应力增高,当上层采空区的应力释放区与下层采空区任一区域重叠时导致围岩压应力降低,并且上下采空区重叠与非重叠区域的交汇处应力变化显著。
(4)应进一步分析多层矿体多采场采空区围岩极限平衡状态,并根据其围岩应力迁移规律和失稳特征合理确定回采参数与回采顺序,以实现安全、高效、经济开采。

