内置式永磁同步电机精确参数的MTPA控制

张晓,史军伟,王越,刘业钊

(1.中国矿业大学 电气与动力工程学院,江苏 徐州 221116; 2.中国矿业大学 信息与控制工程学院,江苏 徐州 221116)

0 引 言

永磁同步电机(PMSM)以其效率高,高功率密度等优点[1],成为当前研究的热点,尤其是转矩电流比较高的内置式永磁同步电机(IPMSM),在电动汽车及工业领域得到了广泛的应用[2-3]。IPMSM的永磁体内置于转子,交、直轴电感不相等,其电磁转矩由永磁转矩和磁阻转矩组成,因此可充分利用磁阻转矩来提高电机的转矩输出能力。在dq同步旋转坐标系下,一条等转矩曲线可由不同的交直轴电流组合产生,在等转矩曲线的电流组合中存在使定子电流最小的一组交、直轴电流组合。最大转矩电流比(MTPA)控制是在输出电磁转矩相等的前提下,通过合理的控制方法使定子电流最小,从而减少铜耗,提高电机的运行效率。永磁同步电机在实际运行中,会不可避免地出现参数变化[4],影响MTPA控制的准确性。

为实现MTPA控制,文献[5]采用费拉里法计算MTPA轨迹,该方法控制原理简单,但该方法需要精确恒定的电机参数。为解决电机参数对控制效果的影响,文献[6]使用工程近似求解策略,采用查表法进行MTPA控制,在控制时查询预先制作的电磁转矩与交、直轴电流关系的表格,但是制表需要大量的测试试验,耗费时间,且电机使用过久后存在老化、永磁体退磁等问题,使最初制定的查询表格存在误差。文献[7]采用迭代法求解MTPA问题,并用拟合曲线将其表示,提高了系统的动态性能,但是不具有通用性,只针对单一的电机。文献[8]采用信号注入法提取MTPA控制下的最优定子电流矢量角,大大减少了前期准备工作,能够较好地实现MTPA控制,但注入信号会产生额外的损耗,且对注入信号的幅值和频率的选取要求较为严格,因此实现较为困难。针对参数辨识问题,文献[9]在直线永磁同步电机上通过测量电流控制器并计算相应的沃尔什一阶系数,实现参数辨识。

针对上述问题,采用遗忘因子递推最小二乘法在线辨识电机参数,并将得到的电机参数用于MTPA控制,该方法能够根据电机参数的变化实时调整MTPA控制轨迹,提高了电机的动态性能和鲁棒性。

1 IPMSM数学模型

在dq同步旋转坐标系下,定子电压方程可表示为[10-11];

(1)

电磁转矩方程:

(2)

运动方程:

(3)

式(1)～式(3)中,ud、uq分别为坐标变换后电机的d、q轴电压;id、iq分别为坐标变换后电机的d、q轴电流;Rs为电机定子绕组电阻;ωe为电机转子的电角速度;Ld、Lq分别为坐标变换后d轴和q轴上的电感分量;ψf为电机转子永磁体磁链;Pn为电机的极对数;Te为电机的电磁转矩;TL为负载转矩;B为阻尼系数;wm为电机转子的机械角速度;J为电机的转动惯量。

2 MTPA原理

由电磁转矩公式可得出,通过对交、直轴电流进行控制即可实现对电磁转矩的控制。在电磁转矩一定的情况下,通过合理的控制策略使交、直轴电流组合得到的定子电流最小,从而实现MTPA控制,MTPA控制的数学表达式可表示为[12]:

(4)

式中is为定子电流。

由拉格朗日乘数法求解极值问题,得到在MTPA控制下的交、直轴电流分别与定子电流的关系式:

(5)

使用式(5)即可实现MTPA控制,控制轨迹如图1所示。

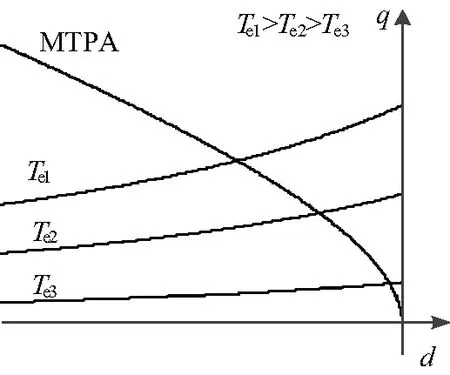
图1 MTPA控制轨迹图

可以看出式中含有较多的电机参数,但在电机运行时参数会不可避免地发生变化,从而使实际MTPA轨迹发生偏离。为凸显电机参数对MTPA轨迹的影响,将式(5)中直轴电流与定子电流的关系重写为:

(6)

其中D为包含电机参数的表达式,其式为:

D=ψf/(Lq-Ld)

(7)

图2为不同D值(即电气参数发生变化)所对应的MTPA控制轨迹曲线。由图2可以看出,要实现精准的MTPA控制必须知道当前运行状态下的电机参数,所以使用遗忘因子递推最小二乘法对电机参数在线辨识。

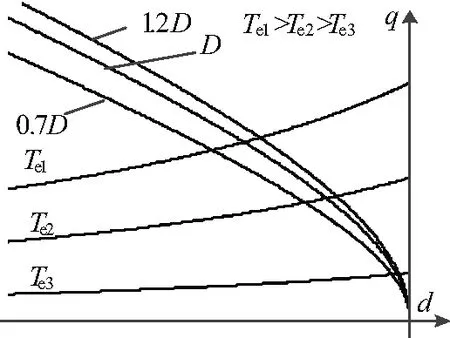
图2 不同D的MTPA控制轨迹图

3 在线参数辨识与MTPA控制

3.1 遗忘因子递推最小二乘法

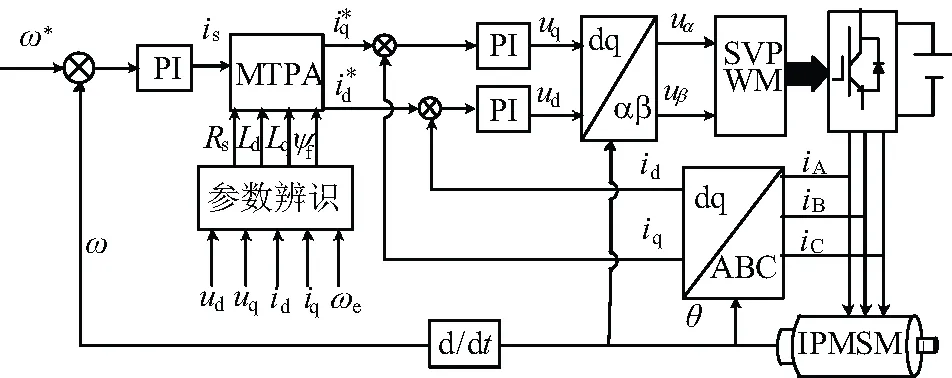
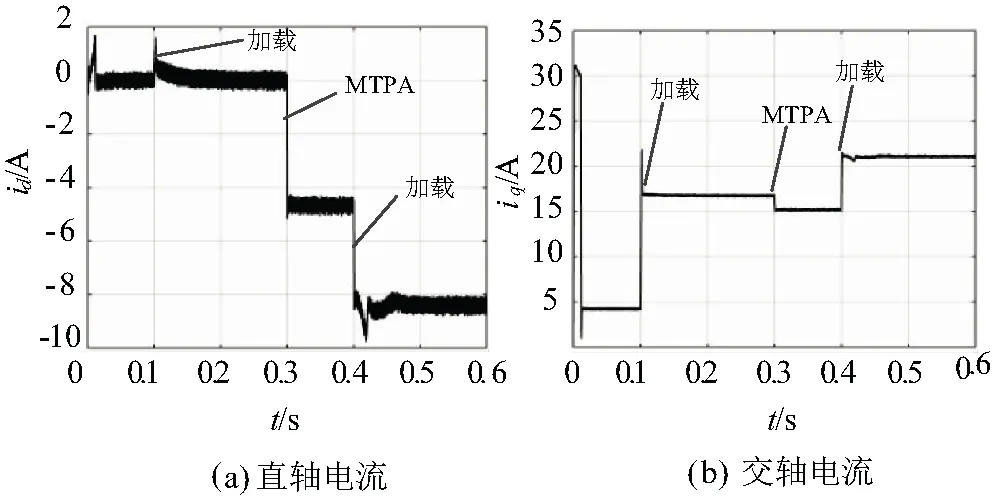
递推最小二乘法存在“数据饱和”的问题[13],文中在递推最小二乘法的基础上引入一个遗忘因子λ(0

取指标函数为[14]:

(8)

式中θ为被辨识参数矩阵;φ(k)为回归信息向量;y(k)为第k次观测的输出向量。

基于上述指标函数,遗忘因子递推最小二乘法的推导公式可表示为:

(9)

3.2 电气参数辨识

辨识的电机参数包括:定子电阻Rs、交轴电感Lq、直轴电感Ld、永磁体磁链ψf。式(1)中的d轴电压方程不包含ψf,所以先用直轴电压方程辨识Rs、Lq、Ld,再利用交轴电压方程辨识ψf。

将dq旋转坐标系下的电压方程改写为矩阵形式并移项得到如下矩阵[15]:

(10)

由于电压方程中含有电流的微分项,现对电流作离散化处理得:

(11)

式中Ts为采样时间。

根据式(8)和式(9)运用遗忘因子递推最小二乘法对Rs、Lq、Ld进行辨识得到。

运用d轴电压方程对永磁体磁链进行辨识,将d轴电压方程进行处理得到:

(12)

运用上述公式即可在线辨识电机电气参数Rs、Lq、Ld、ψf从而将准确的电机参数应用于MTPA控制。

3.3 在线参数辨识的MTPA控制

为解决电机参数变化引起实际MTPA轨迹发生偏离而无法跟踪的问题,将在线辨识的实时电机参数用于计算当前MTPA轨迹,控制框图如图3所示。

图3 基于参数辨识的MTPA控制框图

实现MTPA控制的公式表示如下[16]:

(13)

(14)

4 仿真验证与分析

为验证所述方法的准确性与有效性,利用Matlab/Simulink软件对内置式永磁同步电机精确参数的MTPA控制系统进行了仿真,控制系统框图如图4所示,IPMSM的主要参数如表1所示。

表1 IPMSM参数

图4 IPMSM的MTPA控制系统框图

仿真系统模型中电机带5 N·m负载启动,待系统稳定后在0.1 s时加载到20 N·m。为了表现MTPA控制在减小定子电流方面的性能,在0～0.3 s采用矢量控制中的id=0的控制方法,0.3 s后系统切换到MTPA控制;为验证所述MTPA控制的动态性能和参数辨识的准确性,在0.4 s时突加负载到30 N·m。

采用遗忘因子递推最小二乘法对电机参数辨识的结果如图5所示,可以看出在电机启动和负载突变时电机参数波动较大。负载增量在0.1 s时比0.4 s时多,q轴电流变化幅值大,使直轴电感在0.1 s时波动较大。但交、直轴电感均能在较短的时间内正确跟踪电感的实际值。在图5(c)、图5(d)中定子电阻和永磁体磁链在负载突变时,所用辨识方法的辨识过程均小于0.1 s。所以文中所用遗忘因子递推最小二乘法辨识电机参数收敛速度快,稳态误差小。

图5 电机参数辨识结果

采用上述控制方法实现MTPA控制得到的直轴电流、交轴电流、定子电流和电磁转矩波形图如图6所示。

图6 MTPA控制仿真波形图

从图6可以看出,在0.3 s时由id=0控制切换到MTPA控制后,直轴电流id会大幅增加,交轴电流iq、定子电流is明显降低,因为MTPA 控制实现了交、直轴电流的最佳组合,使定子电流在该负载条件下最小,从而减小铜耗提高运行效率。

在0.4 s突加负载时,在电机参数波动的情况下交、直轴电流快速实现最优组合,电磁转矩能够快速地响应,转矩脉动小,电流波动较小。

5 结束语

针对内置式永磁同步电机在进行MTPA控制时因电机参数变化导致MTPA轨迹发生偏离的问题,将遗忘因子递推最小二乘法在线参数辨识引入MTPA控制中,在线得到的电机参数用于计算当前MTPA轨迹,实现了MTPA轨迹跟随电机参数变化而及时调整。该方法与应用较多的查表法相比极大地减少了工作量和时间,同时也避免了电机在使用过程中的老化、永磁体退磁等问题使最初制作的查询表格不准确的情况,仿真结果验证了所提方法的正确性和有效性。