基于新型B-N窗和改进分区法的三相不平衡度检测

周纲,黄瑞,刘谋海,李丹,胡军华,高云鹏

(1.国网湖南省电力有限公司,长沙 410004; 2.智能电气量测与应用技术湖南省重点实验室,长沙 410004;3.湖南大学,长沙 410082)

0 引 言

三相不平衡是衡量电能质量的重要指标[1]。随着当前智能电网各种冲击性和非线性负载的大量应用,电能质量不断恶化,电压或电流中存在大量负序分量,不仅影响供电质量,也给电力系统安全稳定运行带来隐患[2]。为降低电网不平衡给系统带来的危害,减少因供电质量下降而造成的不必要损失,需对电网三相不平衡进行准确检测与分析[3]。

遵循国标《电能质量 三相电压不平衡》和国际大电网委员会定义,三相不平衡度分为线电压和相电压两种计算方法,在实际检测装置中,通常只能得到相电压的幅值与相角,经过换算才得到线电压,计算过程繁琐[4],而相电压计算方法中相序分量求取涉及平方运算,且相序间相角求取易受电网电压噪声影响,嵌入式系统计算准确性和实时性亟待提高。

检测三相不平衡度分为两个阶段,首先检测电压基波分量的幅值和相位,再应用对称分量法检测出基波分量中的正序、负序和零序相序分量。在基波测量方面,快速FFT变换是常用算法,但非同步采样时存在频谱混叠、频谱泄漏等影响。为此文献[5]提出基于三维空间法向量的三相电压幅值检测算法,但因含有滤波器存在时延,且缺乏相位检测信息。文献[6]提出混合基FFT算法计算基波分量,结合对称分量法计算不平衡度,但采样点基数有限。文献[7]提出改进的S变换检测电压的幅值和相位,但涉及调节参数,难以兼顾检测精度和速度;在相序分量测量方面,因最小二乘法[8]、卡尔曼滤波法[9]易受噪声影响,使相角计算出现误差。文献[10]提出瞬时序分量提取方法获得序列分量幅值相位,但依赖于锁相环精度。基于锁相环检测法响应时间过长和易受电压分量不平衡的影响,文献[11]提到采用双二阶广义积分器的正序电流分量检测方法,并对分离正序电流跟踪补偿。文献[12-13]提出假设检验检测理论,并应用广义似然比求解系统频率的近似极大似然估计值,但受电网频率波动影响大。文献[14]利用向量测量单元进行三相不平衡检测,给出非正常频率下的相序分量的模型和假设检验的框架,但嵌入式系统实现复杂。文献[15]提出基于FBD基波正负序检测算法,但依赖于低通滤波器改进。文献[16-17]提出相量快速算法来计算不平衡度,但对于基波分量的求取精度未做太多介绍,文献[18]提出准同步采样算法和相量快速算法结合来实现不平衡度测量,但递推过程繁琐。文献[19]采用加窗快速傅里叶变换和坐标分区法结合计算不平衡度,解决信号的频谱泄露和栅栏效应等问题,但现有窗函数对于基波分量的求取精度不高。

因此,为实现三相不平衡度的准确检测,文中构建Blackman-Harris窗和Nuttall窗互卷积新型窗函数,其频谱性能结合两窗的旁瓣优势,具有较低的旁瓣峰值,更快的旁瓣衰减速率,推导了新型B-N卷积窗的三谱线改进FFT修正算式,并在原有的坐标分区法基础上增加分区数目,提出改进坐标分区法实现相序分量与不平衡度求解,据此提出基于新型B-N卷积窗和改进分区法的三相不平衡度检测方法,提高了基波计算精度,同时避免复杂开方运算和三角函数运算最后采用仿真实验对文中提出的方法进行验证与分析。

1 三相不平衡度计算

负序电压不平衡度为电压基波负序分量有效值与基波正序分量有效值的比值,零序电压不平衡度为电压基波零序分量有效值与基波正序分量有效值的比值,表达式分别为:

(1)

(2)

式中εn为负序不平衡度;ε0为零序不平衡度;Up为基波电压正序分量;Un为基波电压负序分量;U0为基波电压零序分量。

根据对称分量法原理,可得系统三相相电压和相序分量的关系,表达式为:

(3)

式中α为旋转算子,α=ej2π/3

设三相电压基波幅值分别为|Ua|、|Ub|、|Uc|,相位分别为φa、φb、φc,则相序分量与基波分量的关系可表示为

j(|Ua|sinφa+|Ub|sin(φb)+|Uc|sin(φc)

(4)

(5)

(6)

通过式(4)～式(6)计算,获得相序分量的有效值与相位,再经过式(1)与式(2)可计算出三相不平衡度。

2 新型B-N窗基波分量求解

基波幅值和相位准确检测是相序分量计算与三相不平衡准确检测的基础,而基于优化窗函数改进FFT修正可有效提高基波分量的检测精度。4项Blackman-Harris窗旁瓣峰值电平为-92 dB,4项5阶Nuttall窗旁瓣衰减速率为42 dB/oct,旁瓣峰值电平较小,具有良好的旁瓣性能。因此文中采用4项5阶Nuttall窗与Blackman-Harris窗构造新型B-N混合互卷积窗,分析其归一化频谱,并推导三谱线插值修正计算式。

4项Blackman-Harris窗和4项5阶Nuttall窗均属于余弦窗,其时域表达式为:

(7)

式中M为窗函数项数,n=0,1,….N-1;Blackman-Harris窗的b0=0.358 75,b1=0.488 29,b2=0.141 28,b3=0.011 68;4项5阶Nuttall窗的b0=0.312 5,b1=0.468 75,b2=0.187 5,b3=0.031 25。

通过性能优良的窗函数互卷积构建新型混合卷积B-N窗时域表达式为:

(8)

根据时域卷积定理,获得新型B-N互卷积窗的频域表达式为:

WB-N(ω)=WB(ω)·WN(ω)

(9)

Blackman-Harris窗、4项5阶Nuttall窗及本文构建新型B-N窗的归一化对数频谱如图1所示。

图1 窗函数的归一化对数频谱

由图1可知,与Blackman-Harris窗和Nuttall窗相比,新型B-N卷积窗具有更低的旁瓣峰值和更快的旁瓣衰减速率,显著提升了余弦窗的旁瓣性能,能更好抑制频谱泄露,提高检测结果的准确度。

设电压信号含有H次谐波,以采样频率fs对单相信号采样后得:

(10)

用卷积窗对x(n)进行处理,可得加窗后的离散傅里叶表达式为:

(11)

式中Δf=fs/N为信号平均采样间隔。由于非同步采样和栅栏效应影响,信号实际峰值频点khΔf很难正好位于采样频点,为使电压基波分量计算精度更高,本文利用实际峰值点及其附近两条谱线,计算新型B-N互卷积窗插值下的电压基波分量。

信号频谱最高点对应横坐标为kh,但由于非同步采样,该点并未被采集到,而采集到其附近最大值对应的谱线km,与其靠近右侧和左侧的两根谱线分别为km+1和km-1,令ε=kh-km,则-0.5<ε<0.5,三根谱线对应的幅值分别为y1=|X(km-1Δf)|,y2=|X(kmΔf)|,y3=|X(km+1Δf)|,记:

(12)

将参数ε代入式(12),可得:

(13)

记β=f(ε),求得ε=f-1(β),用函数近似求解拟合法获得参数ε,根据频率与实际频谱最高点间对应关系,可获得频率计算式为:

fh=(kh+ε)Δf

(14)

通过加权设置,可得到电压基波幅值和相位修正式分别为:

A1=

(15)

(16)

同理,用逼近方法求解多项式g(e),经多次拟合求得新型B-N互卷积窗三谱线插值参数e和g(e)计算式分别为:

ε=1.76925764β-0.12413716β3+0.01825458β5-0.00327175β7

(17)

g(ε)=2.31811912+0.32870923β2+0.02421399β4+0.00125990β6

(18)

3 改进分区法三相不平衡度检测

相序分量求取结果与三相基波电压的幅值和相位的精度直接相关,由式(4)～式(6)可知,相序分量需经过三相电压相量的和求模获得,通常求相量和的模有两种方法,即公式法与坐标法,而公式法运算量大,故本文选取建立新型坐标系的坐标法来计算相序分量,在原有以3和4为基底的坐标分区法基础上通过增加分区数建立改进分区法,实现以5为基底,并进一步推导得出5分区、10分区和15分区的不平衡度,比较三个分区下不平衡度检测结果,据此验证构建改进分区法的准确性和有效性。

设有三相电压相量,A、B、C三相电压的坐标分别为A(x1,y1),B(x2,y2),C(x3,y3),则有:

(19)

tanθ=(y1+y2+y3)/(x1+x2+x3)

(20)

式中θ为三相电压相量和的模的相位,在直角坐标系中,若电压A相幅值为Ua,相位为α,则相量A相坐标为(Uacosα,Uasinα),同理B相坐标为(Ubcosβ,Ubsinβ),C相坐标为(Uccosγ,Ucsinγ)。

由式(19)与式(20)可计算出三相电压和的幅值与相位,但涉及开方与三角函数运算,计算量较大,为简化运算,需建立新型直角坐标系。本文取a相所在相量为x轴,则A相坐标为(Ua,0),B相坐标为(Ubcos(φb-φa),Ubsin(φb-φa)),C相坐标为(Uccos(φc-φa),Ucsin(φc-φa)),在新坐标系中相序分量的求取能省去开方与三角函数计算,减少计算量,有效加快相量求取速度,以负序分量Un计算为例建立负序分量坐标图如图2所示。

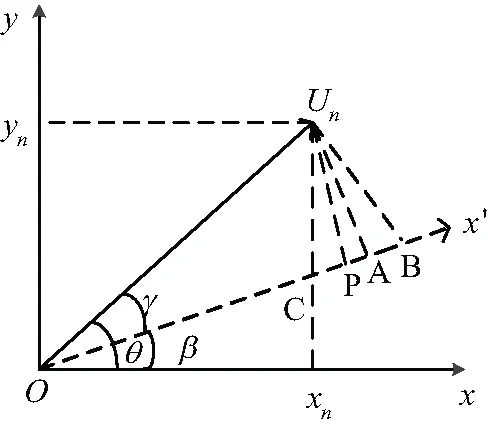
图2 计算负序分量坐标图

由图2可知,负序分量OUn的幅值即为所求负序分量值,而点Un到原点O的距离即为负序分量OUn的幅值。设负序分量Un坐标为(xn,yn),则:

(21)

假定xn>yn,在相量Unxn上任取一点C,延长线段OC到A点,使|OA=OUn|,为计算方便,作UnP⊥OA,BUn⊥OUn,则有:

|OUn|=|OA|=|OC|+|CP|+|PA|

(22)

由图2可知,令θ为相量OUn与x轴的夹角,则θ=arctan(yn)/xn,x’轴为相量计算方便而选取轴,β为x’轴与x轴间的夹角,γ=θ-β,则相量|OC|、|CP|和|PB|分别表示为:

(23)

|CP|=(yn-xntanβ)sinβ

(24)

(25)

因A点位于相量PB之间,所以在相量PA与PB间必存在一个0与1间的系数η,使|PA=ηPB|,即:

(26)

式中η为比例因子,k0=1/cosβ,k1=sinβ,k2=η·

(cosβ)2。

由此可见,相量OUn求取转化为三角函数求和形式,为进一步简化计算量,本文将三角函数运算用简单的线性函数代替,并依据本文提出的以5为基底的改进坐标分区法,进一步分析5分区、10分区及15分区相关系数和不平衡度的检测结果。以xn值为基准建立正方形坐标区域,建立5分区法如图3所示。

由图3可知,在y轴上选取四个点,将y轴分为五等份,即yn1=yn2/2=…yn5/5=xn/5,设OUn在第i分区,则有(i-1)xn/n≤yn≤ixn/n,β为i-1个分区所对应的夹角,有:

(27)

由图2几何关系可得,相量UnA为∠PUnB的角平分线,则:

(28)

式中γ=θ-β。为减少三角函数复杂运算,用一次线性函数y1=b1γ和y2=b2γ分别逼近tanγ、tan(γ/2),则:

(29)

由式(29)可得,η仅由b1和b2决定,不同分区数的η值不同,通过函数拟合得到不同分区的b1,b2和η值如表1所示。

表1 3个分区的b1、b2、η值

根据k0、k1、k2与β的三角函数关系,以5分区和10分区为例仿真,得到5分区和10分区k0、k1、k2值如表2所示。

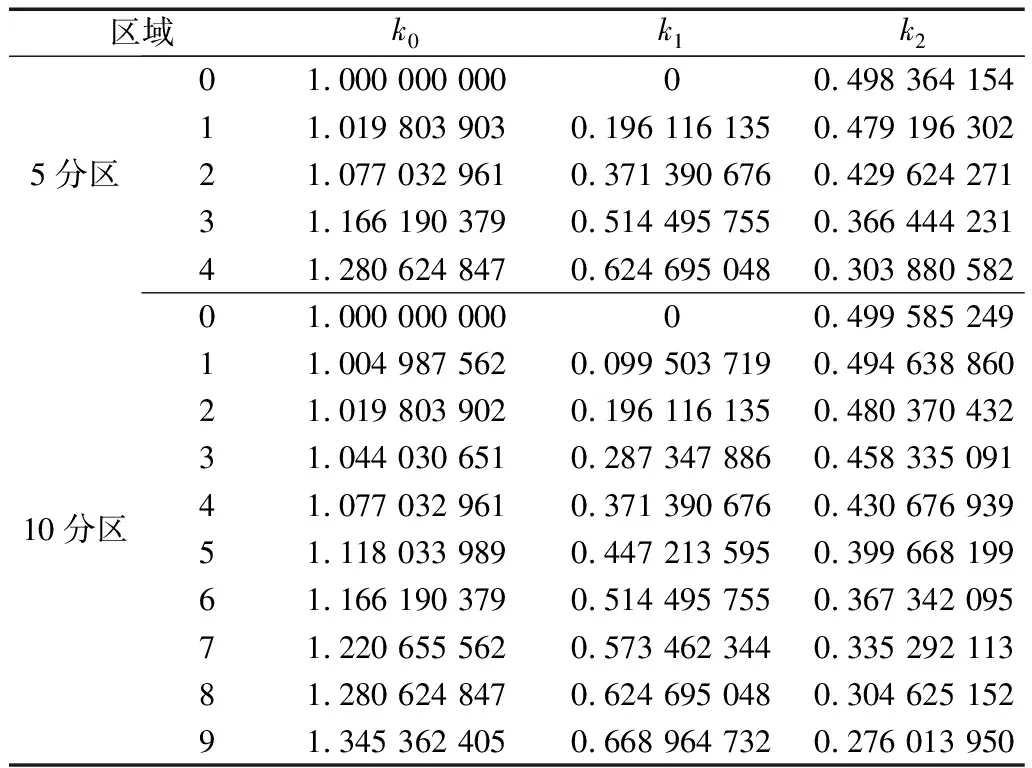
表2 5分区和10分区幅值的系数

当n=5时,设|OUn|在1区,由表2得k0=1.019 803 900,k1=0.196 116 135,k2=0.479 196 302,代入式(26),计算负序分量即|OUn|的值;若xn≤yn,可在x轴进行分区域计算,计算思路与xn>yn一致,依此原理可计算出正序分量与零序分量的值,代入式(1)与(2),计算得出不平衡度的最终结果。

4 仿真实验与分析

为验证文中提出的基于新型B-N窗和改进分区法的三相不平衡度检测方法计算精度,取国标推荐方法为基准值,对三组含基波电压信号和含有五次谐波及高斯白噪声信号进行仿真,其中基波频率为50 Hz,谐波频率fh=hf1,采样频率为fs=8 kHz,采样长度为N=2 048。

4.1 仅含基波的电压信号仿真

对3组仅含基波的A、B、C三相电压信号进行仿真分析,电压信号幅值与相位如表3所示。采用GB/T 15543-2008推荐方法和本文方法求取电压信号的基波分量和相序分量,进而求得三组信号的负序不平衡度(VUFn)和零序不平衡度(VUF0)结果如表4所示。

表3 三相基波电压信号参数

表4 电压不平衡度仿真结果

由表4可知,随着分区数的增加,基于本文方法得到的不平衡度检测结果与国标检测结果接近,经十分区和十五分区仿真得到的结果更接近国标推荐方法的检测值。

为比较不同分区下不平衡度的相对误差,以GB/T 15543-2008方法为真值,不同分区的相对误差表达式为:

(30)

式中R为不同分区下计算的实际值;I为国标推荐方法计算真值。对1-3组电压信号仿真,所得相对误差如图4所示。

图4 不平衡度的相对误差图

由图4可知,五分区电压不平衡度相对误差最低为10-5%左右,而十分区、十五分区的不平衡度误差可达到10-7%～10-6%之间,可见,采用十分区和十五分区得到的仿真效果更好。

为验证文中提出的新型B-N卷积窗函数对不平衡度计算结果的影响,分别采用基于Hanning窗、Blackman-Harris窗和4项5阶Nuttall窗以及本文构建的新型B-N卷积窗,以10分区为例,分别对上述电压信号不平衡度进行计算,得到不同窗函数的电压不平衡度测量相对误差曲线如图5所示。

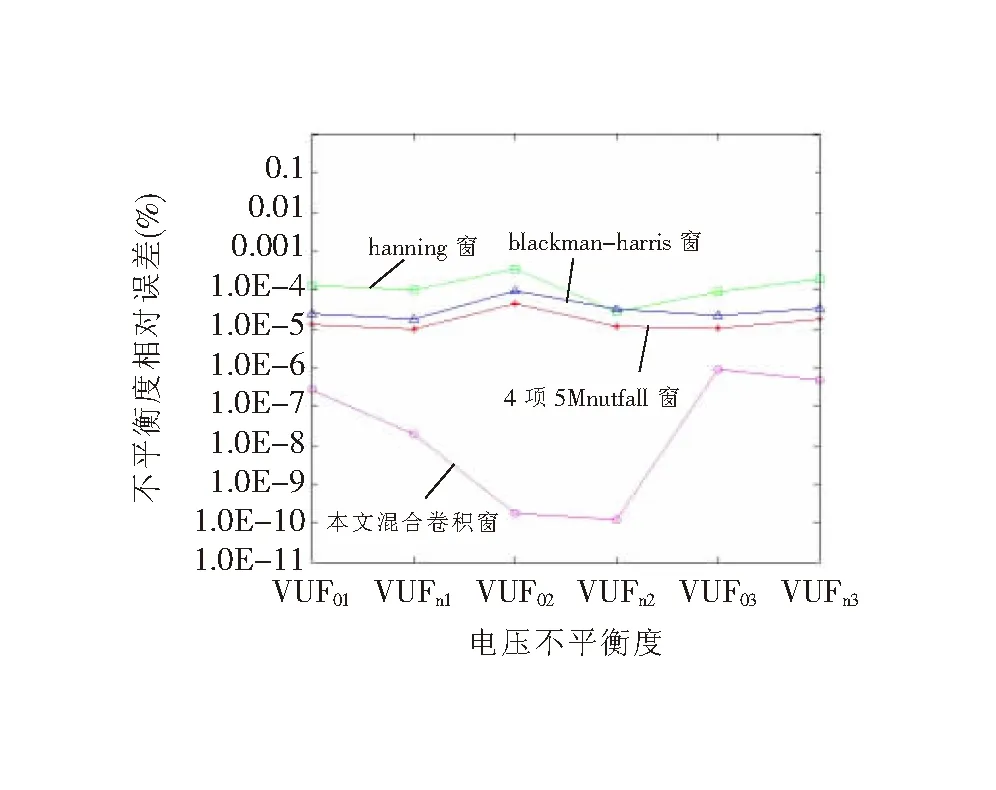
图5 不同窗函数的电压不平衡度相对误差

由图5可知,四种窗函数仿真中Hanning窗得到的不平衡度相对误差最大,应用本文新型B-N卷积窗得到不平衡度的相对误差最小。由此可见,不同窗函数与改进分区法的结合影响不平衡度计算的结果,文中提出的新型B-N卷积窗改进分区法可降低不平衡度计算的相对误差,提高测量的准确度。

4.2 含谐波信号的仿真

非线性负荷常给电网注入大量谐波,为验证本文算法在电压信号含有谐波情况下仍有很好的计算精度,向第四组电压信号中加入七次谐波,仿真信号基波及各次谐波的幅值和相位如表5所示。

表5 含有谐波的三相电压系数

分别以国标推荐方法和本文方法进行仿真得到的不平衡度结果如表6所示。

表6 不平衡度仿真结果

4.3 含噪声信号的仿真

为验证文中算法在含有噪声情况下的计算精度,设第五组电压信号含有3、5、7次谐波,各相电压基波和谐波的幅值与相位参数如表7所示,A相、B相和C相分别加入信噪比为40 dB、18 dB和80 dB高斯白噪声,分别以国标推荐方法和文章方法仿真得到的不平衡度结果如表8所示。

表8 不平衡度仿真结果

由表7和表8可知,文中提出算法在含有谐波和噪声的电压信号下检测出的不平衡度可达到与GB/T方法相同的数量级,其中十分区法和十五分法计算出的电压不平衡度与标准方法计算结果间的误差不超过10-6%,验证了文中算法在谐波和噪声干扰的准确度。

5 结束语

文中提出基于新型B-N卷积窗和改进分区法的三相不平衡度检测算法。新型B-N互卷积窗能准确计算出三相电压的基波和幅值,比传统优化窗函数实现效果更好,以5为基底的改进分区法中10分区和15分区法计算出三相不平衡度的误差更小,提高了不平衡度计算的准确度。从仿真实验与分析的结果可知,文中提出的新型B-N卷积窗结合改进分区法的三相不平衡度检测结果满足GB/T15543-2008的准确度要求,同时避免复杂开方和三角函数运算,减少了运算时间,有效提高了检测的准确性和实时性。