零序电流互感器配大电阻的配电网单相接地故障检测
刘健,刘海,杨晓西,张志华
(1.西安科技大学 电气与控制工程学院,西安 710054; 2.陕西省电力科学研究院,西安 710100)
0 引 言
单相接地故障是配电网中最常见的故障,在中性点非有效接地配电网单相接地故障检测、选线和定位方面已经取得了大量研究成果[1-6]。
零序电流互感器(零序TA)是实现单相接地故障检测的重要部件,其性能直接影响到故障处理效果。电力行业标准DL/T 866-2015《电流互感器和电压互感器选择及计算规程》对TA的参数选型及计算做出了规定。文献[7-8]分析了保护用TA稳态和暂态传变特性。文献[9]讨论了温度对电子式TA和电磁式TA的影响。文献[10]研究了开口式电流互感器的耐直流性能。文献[11]研究了TA的建模方法。文献[12]设计了实验对零序电流过滤器的特性进行了分析。
已有成果均围绕TA二次侧阻抗较小的工况进行研究,而罕见针对TA二次侧配置大负载电阻的情况下TA的特性及其应用的研究报道。实际工作中,经常在国外进口的智能开关的零序TA二次侧观察到有并联较大负载电阻的现象,作者认为这种接法有应用于单相接地故障检测的可能性,但是未见任何说明和解释。
在单相接地故障处理中,检测精度并非最终目的,识别出接地故障发生在区内还是区外,从而正确地选线和跳闸才是最终目的所在。零序TA二次侧并联较大电阻虽然有可能降低了其精度,但是却可以放大二次侧信号,尤其是在高阻接地导致一次侧零序电流较小时,还有可能使其故障特征更加明显,为单相接地检测提供方便。另外,这种做法可以省去二次侧电流互感器,使检测电路更加简单。
探讨零序TA二次侧配置大负载电阻时的特性,并以电力系统中占比超过70%的中性点不接地配电网为例,探讨零序TA二次侧配置大负载电阻的单相接地故障检测方法的应用可行性。
1 零序电流互感器配大负载电阻时的特性
1.1 等效电路
零序TA等效电路如图1所示,将一次侧参数等效至二次侧,一般情况下一次侧绕组电阻和漏抗较小,折算至二次侧时可忽略不计。图中I0为零序TA一次零序电流;Is为二次电流;Im为励磁电流;Kn为额定变比;Es为二次感应电势;U2为负载电压;Zm为励磁阻抗;Z2为二次绕组阻抗;R为负载电阻。

图1 零序TA等效电路
零序TA基本变换式为:
I0/Kn=Is+Im
(1)
零序TA比值误差εi为:
(2)
将式(1)两边同乘以R,联立式(2),有:
(3)
式中Kn=N1/N2,N1和N2为一次和二次绕组匝数;I0、Is和Im均为均方根值。
当零序TA误差较小时,其比值误差εi和相角误差δ的表达式可近似表示为:
sin(φ+θ0)×100%
(4)
cos(φ+θ0)×3440
(5)
式中μ为铁芯磁导率;l为铁芯平均磁路长度;Ac为铁芯有效截面积;φ为二次回路阻抗角;θ0为损耗角;f为电源频率。
通过式(4)和式(5)可知,当I0不变,R增大时,εi和δ增大,即铁芯中励磁电流增大,因此Es和U2增大,且由式(3)可知U2增大(1+εi)R倍。当R+Z2>>Zb,R>>Z2时,U2≈Es,φ≈0,Es与Is同相位。Zb为零序TA额定负载阻抗值。给出了此时TA向量图,如图2所示,Φ为铁芯磁通。

图2 零序TA配大负载电阻向量图
随着负载电阻R的增大,零序TA的铁芯会发生饱和现象,即铁芯磁通饱和,U2不再变化。TA饱和后式(1)~式(3)依然成立,而式(4)和式(5)为零序TA误差较小时的近似计算公式,因此式(4)和式(5)失效,此时εi需用式(3)计算,而δ则需通过实验进行测量。
由于TA饱和后依然满足电磁感应原理,因此,有:
(6)
其中:
B=μ(H+M)
(7)
Hl=N1im
(8)
联立式(7)和式(8),有:
(9)
式中B为磁通密度;H为磁场强度;M为磁化强度;es为二次感应电势瞬时值。由式(6)可知制约es的因素,即制约u2的因素,主要有Ac、N2和B;由式(9)可知B随l减小而增大。因此在相同的使用条件下,二次绕组匝数更多、铁芯有效截面积更大以及铁芯平均磁路长度更小的零序TA,输出的二次电压信号更大。
为进一步研究增大R对零序TA传变特性的影响,分析零序TA输出特性,因此建立零序TA仿真模型,进行仿真分析。
1.2 仿真分析
基于Jiles-Atherton理论[13-14],对零序TA稳态传变特性进行仿真。根据工程实际的典型值,TA取额定变比为150/5 A,额定二次容量Se为2 VA,二次绕组电阻为0.01 Ω,二次漏抗为0.02 mH。
考虑到发生高阻接地故障时故障电流只有几百毫安,中性点不接地系统电容电流一般小于10 A,因此在仿真分析中,I0的取值范围为0.5 A ~10 A。图3给出了I0分别为0.5 A和10 A时,U2-R仿真曲线。
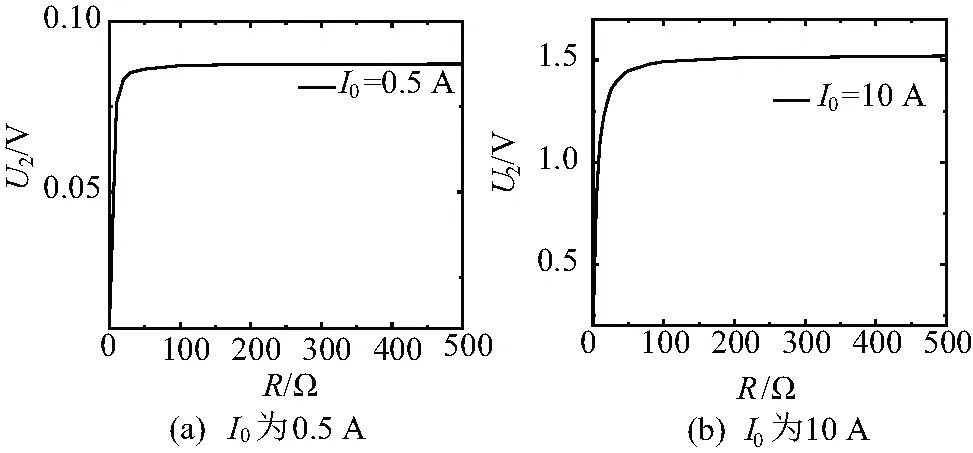
图3 U2-R仿真曲线
由图3可知,随着R增大,U2逐渐增大,当R达到一定值后,U2呈饱和趋势不再显著增大。当I0为0.5 A,R约为50 Ω时,U2呈饱和趋势;当I0为10 A,在R约为100 Ω时,U2呈饱和趋势。为使得I0在0.5 A~10 A时,U2输出值始终保持最大,TA二次侧所配大电阻R的阻值应大于100 Ω。
为进一步分析不同R时,零序TA输出特性,分别对R为1 Ω、12 Ω、122 Ω和200 Ω的情况进行仿真。图4给出了I0小于20 A时,不同R对应的U2-I0仿真曲线。

图4 U2-I0仿真曲线
由图4可知,随着R增大曲线斜率也在增大,表明增大R使得零序TA的响应更加灵敏。但是随着R的增大,曲线的非线性程度也逐渐增大,且122 Ω以上时对斜率的增大程度逐渐减弱,因此推荐采用100 Ω~122 Ω。
1.3 实验验证
以工程中常用的LXK-φ120型零序TA为例,搭建如图5所示的零序TA输出特性测试平台进行实验研究。被测零序TA变比为150/5 A,额定容量为2 VA,准确等级为5P10;电源为ONLLY系列微机型继电保护测试系统,其每相输出电流有效值为0~40 A。

图5 零序TA输出特性测试实验电路
实验主要步骤:分别取R为1 Ω、12 Ω、122 Ω和200 Ω进行试验,将一次电流从零开始缓慢增加至20 A,记录对应的U2波形。图6给出了不同I0和R时,U2的实测波形图。
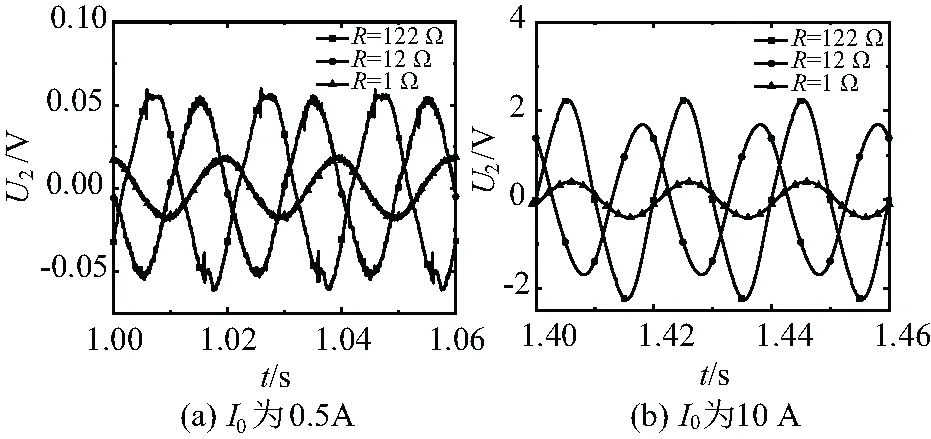
图6 实验过程中U2的波形
图7为I0<20 A时,U2的均方根值与I0的关系的实验结果。

图7 U2-I0实验曲线
由图7和图4对比分析可知,仿真结果与实验结果吻合。通过FFT对实验数据进行处理,定量分析计算不同I0和R时,U2、实际功率S、εi以及δ的值,其中S=Is2(R+Z2),δ为负载电压U2基波相位与I0相位之差。计算结果如表1所示。
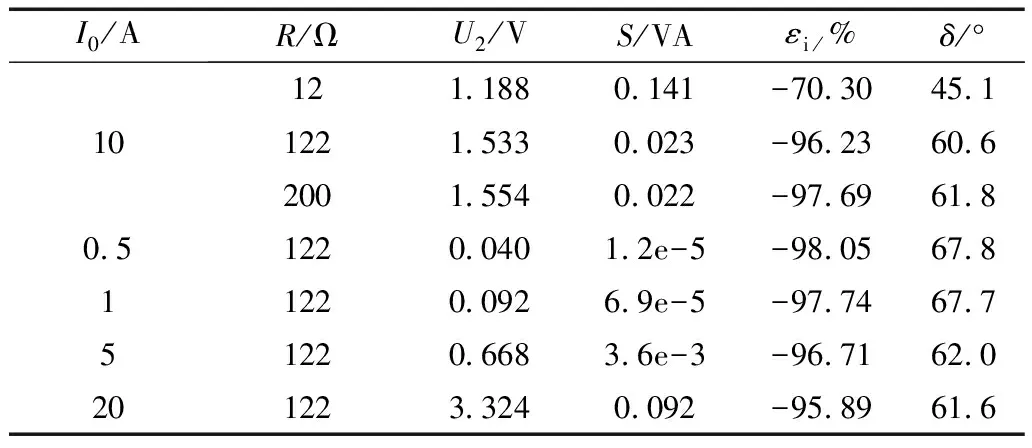
表1 零序TA实验参数
通过表1可知,当I0不变时,随着R增大,εi、δ和U2均增大,实际功率S减小。当R不变时,随着I0增大,εi和δ均在一定范围内变化,且其值远大于额定误差限值,但误差的相对变化量较小,其中εimax-εimin=2.06%,δmax-δmin=7.2°。若在实际应用时需要提高比差和角差的精度,可通过查表的方式进行修正。对于文中的应用方式而言,上述比差和角差已经能够满足要求,因此不需要修正。
2 单相接地检测
2.1 基本方法
由第1节可以看出,零序TA配大负载电阻时,尽管在一次电流较大时二次波形会有一些畸变,并且U2与I0成非线性关系,但是U2与I0仍是单调关系,因此仍可以根据二次侧电压U2反映一次侧零序电流的大小,从而进行单相接地检测。
由第1节还可以看出,当一次零序电流I0较小时U2与I0成近似线性关系,并且U2也比较大从而便于检测,这就为零序电流较小的高阻接地的检测提供了方便。
为了能够有效地进行单相接地检测,负载电阻R的参数很关键,在中性点不接地系统中可能遇到的最大零序电流时(一般小于20 A),其设计原则需同时满足下列条件:
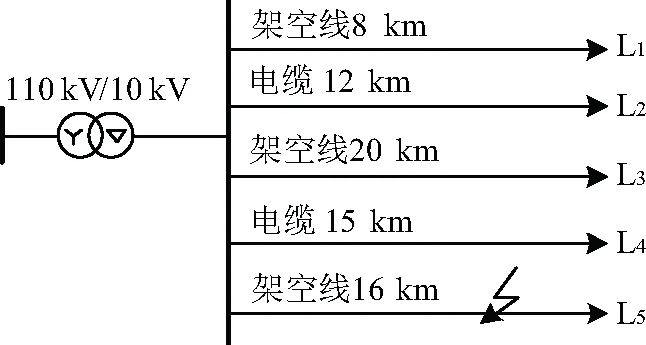
(1)U2 (2)流过R的功率PR 例如,对于1.3节例子中的150/5 A零序电流互感器的情形,R>100 Ω时均可满足要求。 图8(a)为一个基于零序TA配大电阻的用户侧分界开关单相接地保护装置(WT)的构成,当U2大于阈值电压UREF时,比较器输出置位,驱动跳闸继电器动作。图8(b)为该装置的布置示意图。图8中CB为变电站出线开关,F为线路分段开关。 图8 单相接地保护装置原理图 由于用户10 kV线路很短,一般不会超过0.5 km,而架空线每km电容电流小于0.03 A(电缆线路电容电流根据芯线截面不同,最大为1.8 A/km)[15],也即用户线路自身电容电流不超过0.015 A(电缆线路为0.9 A),因此,可将该分界开关的一次侧动作零序电流整定为1 A,超过这个值则反映一定是用户内部发生了单相接地,对应的接地过渡电阻为5.5 kΩ。对于150/5 A的零序TA,一次侧1 A对应的二次电流值仅为33.3 mA,但是配负载电阻大于100 Ω时,对应的U2大于90 mV,也即UREF可取为90 mV,且不需要配置二次TA。根据第1节的论述,随着R的进一步增大,曲线的非线性程度也逐渐增大,且122 Ω以上时对斜率的增大程度逐渐减弱,因此推荐采用100 Ω~122 Ω。 图9为一个基于零序TA配大电阻的单相接地选线装置示意图。零序TA采集各条出线零序电流信号,通过负载电阻R将U2信号输送至选线装置进行处理,判断故障出线。 图9 单相接地选线装置原理图 在MATLAB/Simulink中建立中性点不接地配电网仿真模型。仿真模型如图10所示。 图10 仿真模型 图10中,变压器为110 kV/10 kV,采用Y/Δ接线方式,额定容量为20 MVA。系统包含3条架空线路(L1、L3和L5),2条纯电缆线路(L2和L4),单相接地故障发生在线路5(L5)8 km处。各线路参数如表2所示。 表2 仿真模型线路参数 文献[16-18]在不同场景下经过反复实测接地电阻的结果显示,接地电阻最小为18.84 Ω,最大为几MΩ。在仿真时设置接地过渡电阻范围为20 Ω~10 000 Ω。 图11给出了各线路稳态零序电流(I0)与接地过渡电阻(Rg)的关系曲线。 图11 各线路零序电流与接地过渡电阻的关系曲线仿真结果 由图11可知,在Rg为20 Ω~10 000 Ω时,故障线路I0为0.488 A ~19.1 A。根据第1节的论述,随着R的进一步增大,曲线的非线性程度也逐渐增大,且122 Ω以上时对斜率的增大程度逐渐减弱,因此推荐采用100 Ω~122 Ω。以R为122 Ω为例,对零序TA的单相接地检测能力进行仿真验证,并与R为0.04 Ω的情况进行对比。 图12给出了Rg为20 Ω~10 000 Ω,R为122 Ω和0.04 Ω时,U2与Rg的关系曲线以及Is与Rg的关系曲线。 图12 线路零序TA输出信号对比曲线 由图12(a)可知,当Rg为20 Ω~10 000 Ω时,在L5中零序TA二次电压有效值U2-R122为0.039 V~3.185 V,两条线路零序TA二次信号差值ΔU2=U2-L5-U2-L4为0.031 V~2.328 V。 由图12(b)可知,当Rg为20 Ω~10 000 Ω时,在L5中零序TA二次电流有效值Is-R0.04为0.016 A~0.635 A,两条线路零序TA二次信号差值ΔIs=Is-L5-Is-L4为0.011 A~0.432 A。 为了对比传统零序电流检测方法和文中论述的零序TA配大电阻检测方法在单相接地选线时的效果,定义R=0.04 Ω时单相接地所在馈线与正常馈线零序TA二次侧电流之差的相对值KI为: (10) 定义R=122 Ω时单相接地所在馈线与正常馈线零序TA二次侧电压之差的相对值KU2为: (11) 根据仿真结果,可以做出KI和KU2与Rg关系曲线,如图13所示。 图13 KI和KU2与Rg关系曲线 由图13可见,在单相接地选线应用中,论述的检测方法比传统零序电流检测方法的故障特征更明显,对高阻接地的情形改进效果明显。 对于中性点不接地配电网,零序电流互感器配适当的大负载电阻,可以直接利用其二次侧电压实现用户侧单相接地保护和变电站单相接地选线,而不需要配置二次电流互感器,使装置构成更加简单。 在单相接地选线应用中,零序电流互感器配适当的大负载电阻并检测二次侧电压的方法比传统零序电流检测方法的故障特征更显著,尤其是对于高阻接地的情形改进效果更为明显。2.2 用户侧分界开关单相接地保护装置

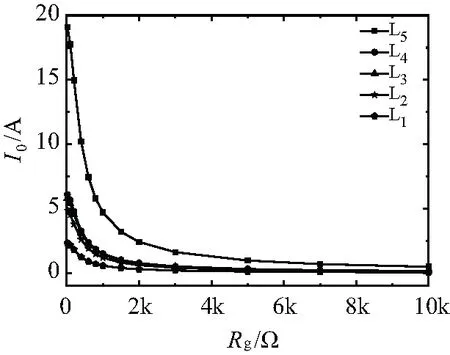
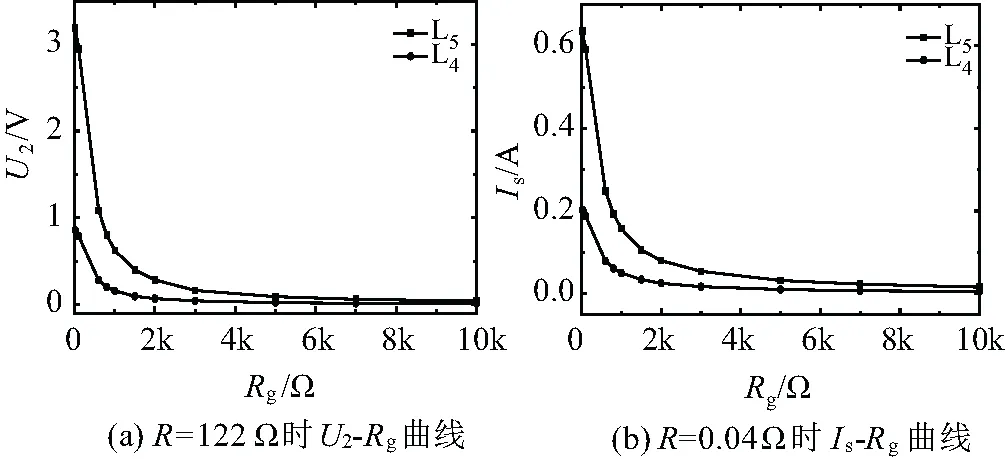
2.3 单相接地选线装置
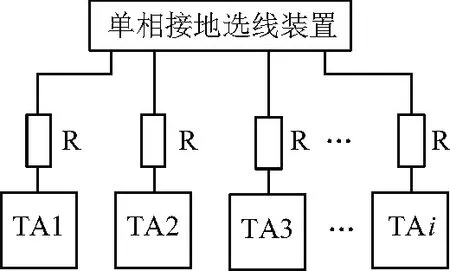
3 单相接地检测性能仿真验证


4 结束语

