模糊惯性BAM神经网络固定时间同步
叶宜豪,江明辉,章雅丹
(三峡大学理学院 湖北 宜昌 443000)
0 引言
1987年Kosko首次提出双向联想记忆神经网络,简称BAM神经网络[1]。它是由两层相互关联的神经网络构成的,比单层神经元组成的神经网络更复杂。随之,BAM神经网络的全局渐进同步[2]、全局渐进稳定[3-4]、全局指数稳定[5]、鲁棒稳定性[6]被广泛研究。在神经网络中,惯性项的引入会使得系统产生复杂的动力学现象,模糊逻辑的加入又可以表达和处理不确定信息。因此,模糊惯性神经网络更贴合实际应用,也吸引了大量学者的注意[7-12]。在惯性项的处理上,大多数文献采用降阶法即使用变量替换法将惯性项转化为一阶项再进行研究,而文献[13]提出一种新的非降阶法,通过构造Lyapunov函数和反馈控制器直接对神经网络系统进行分析。
众所周知,对系统同步控制的研究具有非常重要的意义,它已被广泛应用于安全通信、生物学和信息处理[14-16]等领域。根据收敛时间不同,可以分为无限时间和有限时间类型。例如,渐近同步和指数同步是无限时间类型,而有限时间同步和固定时间同步则是有限时间类型。在实际应用中,需要考虑成本和机器的使用寿命, 所以有限时间类型更具应用价值, 也取得了一些好的成果[17-23]。由于有限时间同步的沉降时间与初值有关,但在实际中很难计算出系统的初值,因此对沉降时间与系统初值无关的固定时间同步的研究变得尤为重要。
通过查阅文献,不难发现目前对于模糊惯性BAM神经网络同步性质的研究相对较少。因此,本文拟采用非降阶法对具有时变无界时滞的模糊惯性BAM神经网络的固定时间同步进行研究。一方面,证明系统平衡点存在的唯一性。另一方面,更正了文献[8]中定理1收敛时间的错误,并给出详细的证明。最后,使用改正后的固定时间稳定性定理得到系统固定时间同步判据。
1 预备知识
本文中,记i∈={1,2,…,n},j∈I*={1,2,…,m},为实数集,n为n维实空间,对于连续有界函数f(t),定义
考虑以下具有时变无界时滞的模糊惯性BAM神经网络
(1)
其中
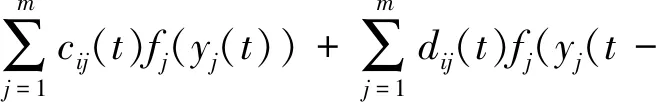

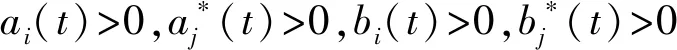
初始条件为
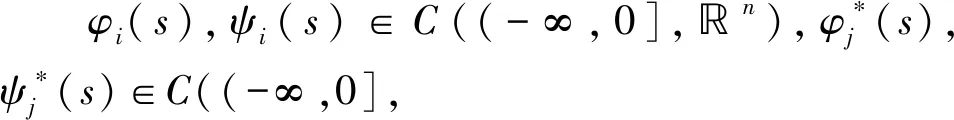
以系统(1)为驱动系统,则响应系统为
(2)
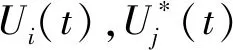
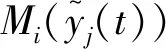
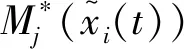
初始条件为
(3)
假设1对任意的m,n∈, 存在常数Lj>0和Li*>0, 使得
定义1[13]如果存在不依赖于初始条件的t0>0,满足
则系统(1)和系统(2)在时间t0时达到固定时间同步。
引理1[24]若θij,oij,xj,yj∈,则
引理2[13]若ai≥0,0
引理3[8]如果存在一个连续、正定和径向无界函数V(x):n→,使得对系统的任意解x(t)都有
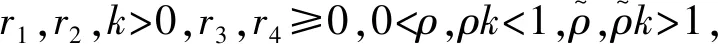
注1这里需要指出上述引理中的稳定时间应该为
证明首先根据文献[8]中第一部分证明,知系统(1)全局有限时间稳定。下面我们只需证明稳定时间有上界。
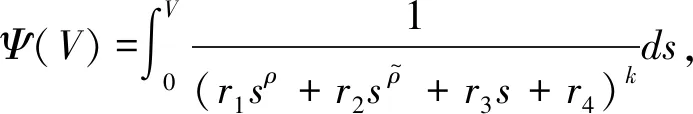
即有
T(x(0))=Ψ(V(x(0)))
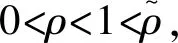
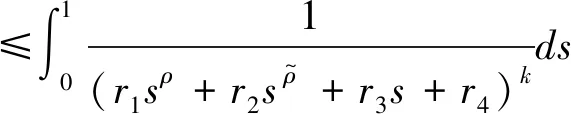
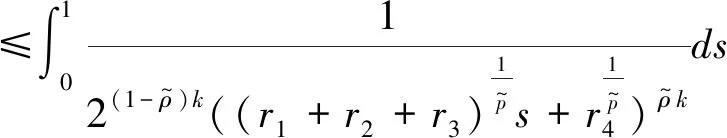
(4)
当V(x(0))>1,有

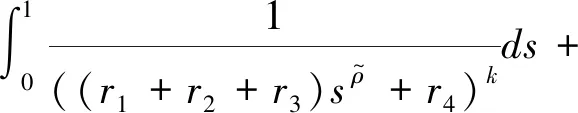
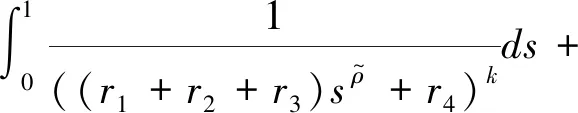
(5)
结合(4)和(5),得
根据定义1,我们得到系统(1)是固定时间稳定,且
2 平衡点的存在唯一性
定理1若假设1成立,且
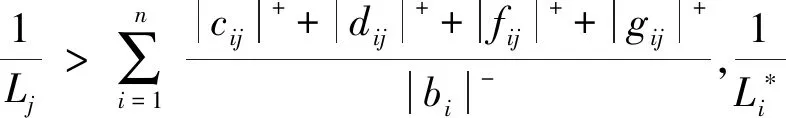
(6)
则系统(1)具有唯一的平衡点。
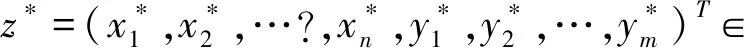
(7)
即
(8)
为证明平衡点的存在唯一性,只需证明方程组(8)只有唯一解。考虑以下映射

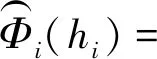
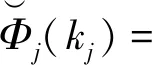
(9)
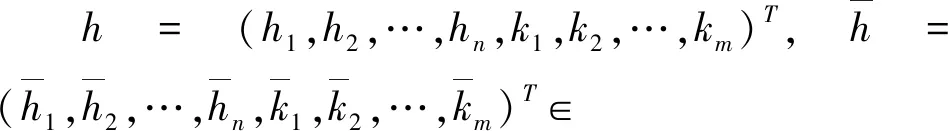
由假设1和引理1,得
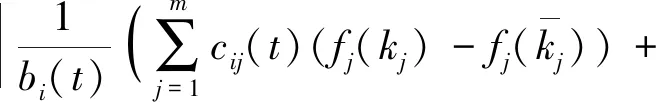
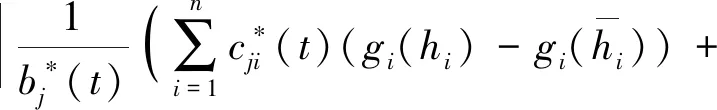
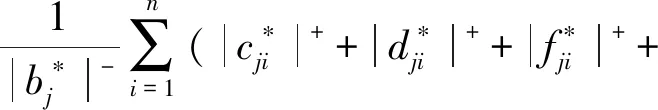
(10)
根据(10)和条件(6),有
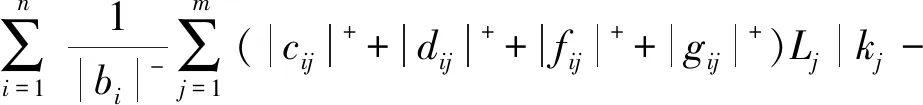
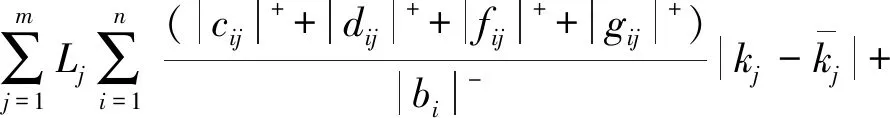
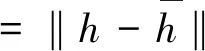
显然映射Φ是一个压缩映射,因此方程组(8)有唯一解,即z*是系统(1)的唯一平衡点。
3 固定时间同步
设计如下控制器
(11)
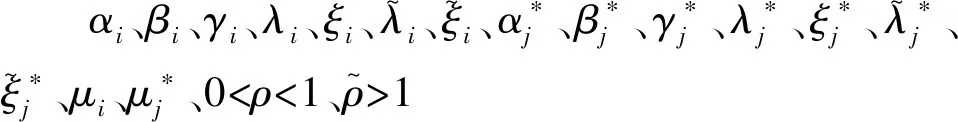

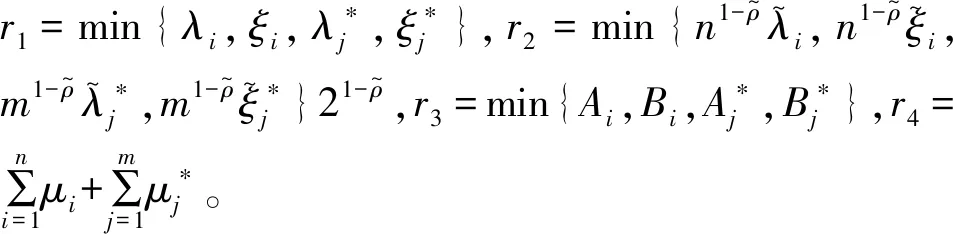
证明构造以下Lyapunov函数
V(t)=V1(t)+V2(t)

首先,沿误差系统(3)计算V1(t)的导数,并由引理1得

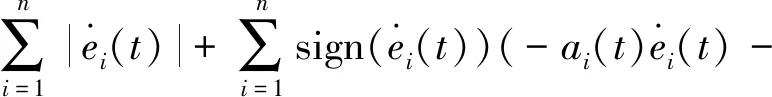

(12)
同理,有
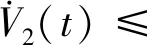
(13)
由(12)和(13),得


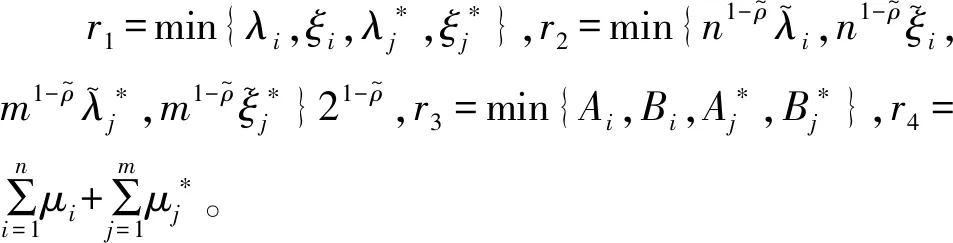
最后,根据引理3,驱动响应系统(1)和(2)将实现固定时间同步,且
4 数值示例


图1 系统状态轨迹
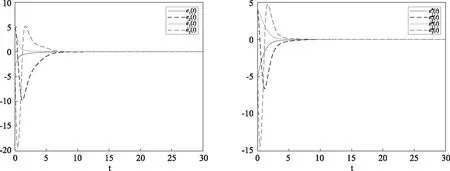
图2 误差和误差导数
5 结论
本文证明了一类具有时变无界时滞的模糊惯性BAM神经网络平衡点存在唯一性,指出并更正文献[8]中定理1的错误,然后利用非降阶法以及更正后的固定时间稳定性定理得到其固定时间同步的充分条件。最后,通过数值模拟验证了结论的正确性。

