2004-2018年葫芦岛市气象因素对细菌性痢疾发生的影响研究*
蒋 涛 施海龙 翟 星 许东东 张明志 沈铁峰 黄德生,5△ 关 鹏△
【提 要】 目的 细菌性痢疾仍然是很多地区重要的公共卫生问题之一,本研究旨在探讨气象因素对细菌性痢疾发生的影响。方法 收集辽宁省葫芦岛市2004-2018年细菌性痢疾月别发病数据,从国家气象信息中心收集该地区月别气压、气温、蒸发量、降水量、降水天数、风速、日照时数、日照百分比和相对湿度等数据。基于广义相加模型探讨气象因素和细菌性痢疾发病数之间的关系。结果 多数模型的决定系数(R2)均超过0.5。气温、降水和湿度与细菌性痢疾的发生呈正相关,气压和日照与细菌性痢疾的发生呈负相关。结论 葫芦岛市细菌性痢疾的发生与气象因素密切相关,应根据细菌性痢疾的流行特征和气象因素的变化制定相应的防控措施,降低疾病的发生风险。
细菌性痢疾是一种最常见的痢疾类型,虽然其发病率呈下降趋势,但在某些地区仍然是重要的公共卫生问题之一[1-3]。细菌性痢疾的发生存在着明显的季节性,在夏秋季节发病率升高[4-5]。气象因素对于细菌性痢疾的影响日益受到国内外研究者的重点关注,气象因素既影响病原体的生长繁殖速度,也影响易感人群的生活方式[6-7]。探究或明确细菌性痢疾的发生与气象因素间的关系有助于精准地预测细菌性痢疾疫情的发展态势,进而基于所发现的相应规律对细菌性痢疾进行精准的预防和控制。本研究利用辽宁省葫芦岛市2004-2018年的气象因素和细菌性痢疾的发病数据,基于广义相加模型(generalized additive model,GAM)来探索气象因素对于细菌性痢疾发病的影响。
资料与方法
1.数据来源
通过辽宁省葫芦岛市疾病预防控制中心收集葫芦岛市2004年1月-2018年12月的细菌性痢疾月别报告发病人数。考虑到月度气象因素的滞后效应,本研究中所收集的气象因素起始时间早于传染病数据6个月;通过国家气象信息中心(http://data.cma.cn)收集葫芦岛市2003年7月-2018年12月葫芦岛市的月别气象数据。月别气象数据主要包括平均气压(hPa)、最低气压(hPa)、最高气压(hPa)、水汽压(hPa)、平均气温(℃)、最高气温(℃)和最低气温(℃)、降水量(mm)、降水天数(天)、平均风速(m/s)、日照时数(h)、日照百分比(%)和平均相对湿度(%)。
2.方法与原理
(1)广义相加模型(generalized additive model,GAM)
GAM是传统广义线性模型的非参数拓展,该模型可以有效处理解释变量与效应变量间复杂的非线性关系,其中部分线性预测因子根据解释变量的平滑函数之和确定[8]。GAM中这些函数的确切参数形式未知,每个函数的平滑度也未知。本研究基于Poisson分布进行多重平滑参数估计,以细菌性痢疾月别病例数为效应变量,平滑气象因素为协变量,预测病例数。逐个进行单个协变量和多变量的GAM,以找出气象因素与细菌性痢疾发病数之间的关系。
(2)GAM的软件实现
本研究采用R软件(www.r-project.org,version 4.2.3)中的mgcv软件包来进行GAM的构建。
结 果
1.辽宁省葫芦岛市细菌性痢疾病报告病例数的时间分布
2004-2018年葫芦岛市细菌性痢疾的累计病例数为1753例,月平均发病率为0.36/10万,月发病率范围为0~2.22/10万,高峰期为每年的7月或8月,详见图1、2。
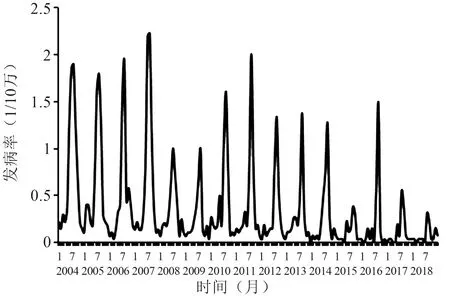
图1 2004-2018年葫芦岛市细菌性痢疾发病率线图
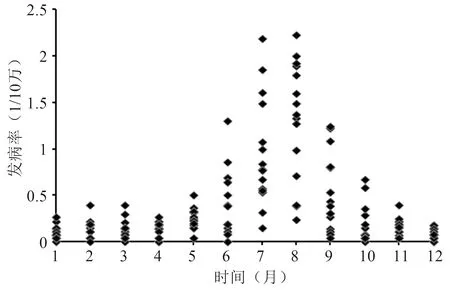
图2 2004-2018年辽宁省葫芦岛市细菌性痢疾发病率散点图
2. 气象因素的滞后效应估计
Unmodified的平滑度可以通过广义交叉验证、赤池信息准则(Akaike information criterion,AIC)、限制最大似然等进行选择。在本研究中,滞后效应由最小的AIC来确定,AIC使用模型的估计自由度来代替通常的自由度。表1显示,气压、降水和日照与细菌性痢疾发病之间有一个月滞后效应,而温度和湿度的月滞后效应未发现统计学意义。

表1 基于AIC的最佳滞后广义相加模型
GAM 的拟合结果
1.气温与细菌性痢疾的关系
GAMs月别最低气温、最高气温、平均气温、平均最低气温和平均最高气温的GAM的调整决定系数分别为0.714、0.568、0.632、0.743和0.784。与细菌性痢疾最相关的是平均最高气温,它可以解释细菌性痢疾变化的81.3%,如图3所示。结果表明,平均最高气温与细菌性痢疾的发生呈正相关。模型拟合的估计自由度为 4.998。当温度为0℃时,相对危险度(relative risk,RR)的自然对数约为-0.9;当温度为20℃时,RR的自然对数为-0.2;随后开始单调增加,当温度达到28度时,RR的自然对数为1.8。
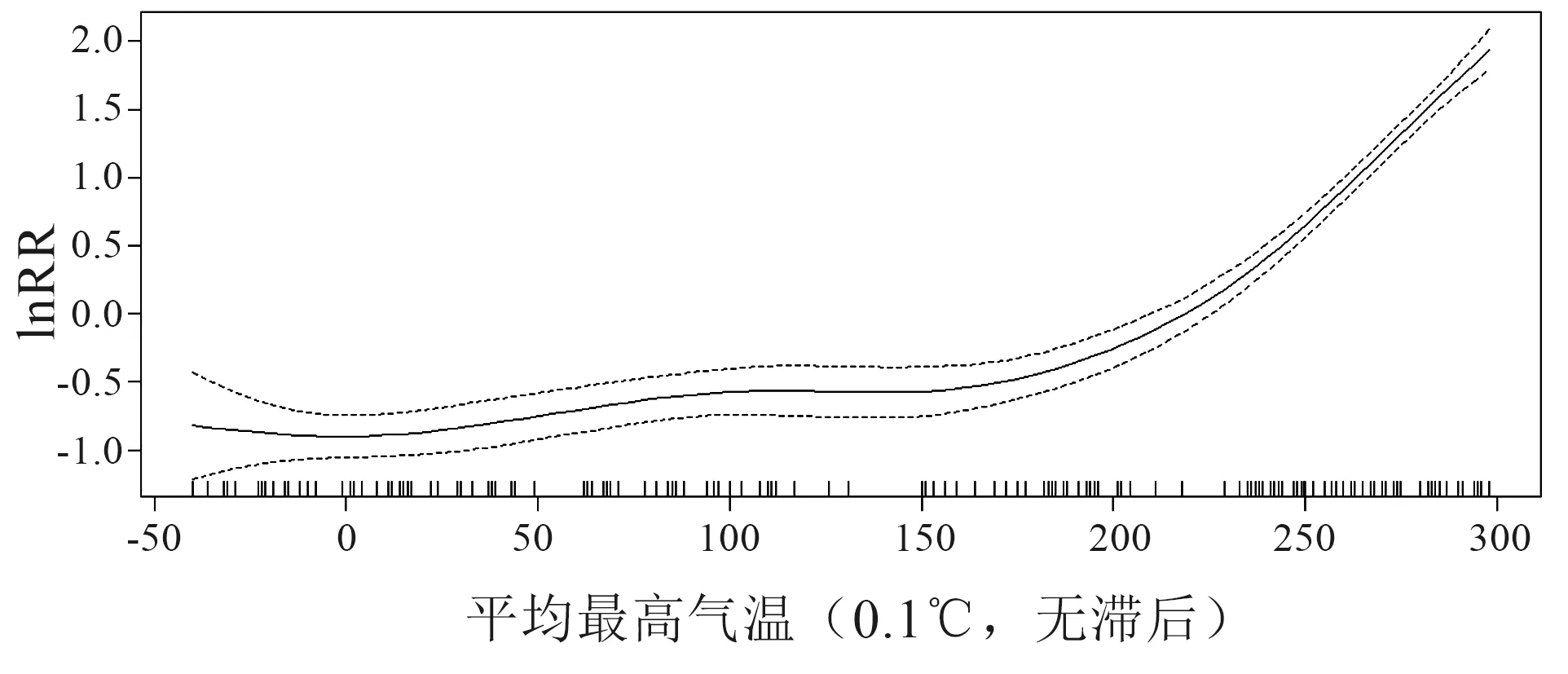
图3 基于月平均最高气温的广义相加模型拟合曲线
2.气压与细菌性痢疾的关系
月别最低气压、最高气压和平均气压的GAM调整决定系数分别为0.516、0.732和0.737。与细菌性痢疾最相关的是平均气压;估计自由度为7.409,可以解释细菌性痢疾变异的79.0%。气压与细菌性痢疾的发生呈负相关,当气压为1002.5 hPa时,RR的自然对数为1.5;当气压为1022.5 hPa时,RR的自然对数为-0.8,见图4。

图4 基于月平均气压的广义相加模型拟合曲线
3.降水与细菌性痢疾的关系
月降水量和降水大于等于0.1mm的日数的GAM调整决定系数分别为0.471和0.573。与细菌性痢疾最相关的是降水大于0.1mm天数;估计自由度为8.811,可占细菌性痢疾变异的63.7%。降水与细菌性痢疾的发生呈正相关,当月降水天数为0时,RR的自然对数低于-0.6。随着降水天数的增加,RR的自然对数迅速上升。当月降水天数达到12天时,RR的自然对数达到1.6,如图5所示。
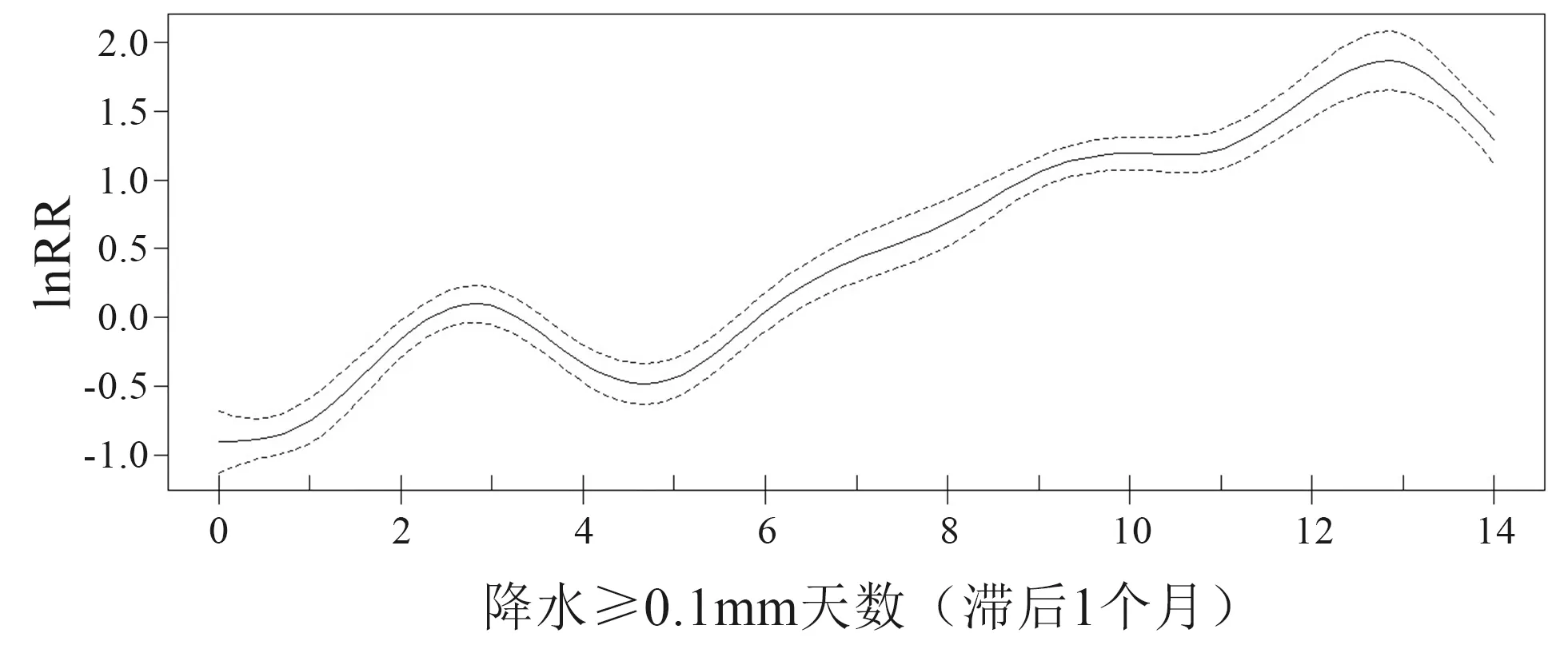
图5 基于月降水≥0.1 mm天数的广义相加模型拟合曲线
4.湿度与细菌性痢疾的关系
GAMs月平均相对湿度和平均水汽压的调整决定系数分别为0.604和0.768。与细菌性痢疾最相关的是平均水汽压,它可以解释细菌性痢疾变化的80.6%。水汽压与细菌性痢疾的发生呈正相关,估计自由度为8.074。当水汽压为5 hPa时,RR的自然对数为-0.6;随着水汽压的增加,RR的自然对数开始增加并迅速上升;当水汽压达到15.5 hPa时,RR的自然对数达到0.8,如图6所示。

图6 基于月平均水汽压的广义相加模型拟合曲线
5.日照与细菌性痢疾的关系
月别日照时数和日照百分比的调整决定系数分别为0.184和0.593。与细菌性痢疾最相关的是日照百分比,它可以解释细菌性痢疾变化的65.1%,如图7所示。日照的百分比与细菌性痢疾的发生呈负相关,估计自由度是7.005。当日照百分比为33%时,RR的自然对数为1.9;随着日照百分比的增加,RR的自然对数开始减小;当日照百分比上升到80%时,RR的自然对数下降到-0.8。
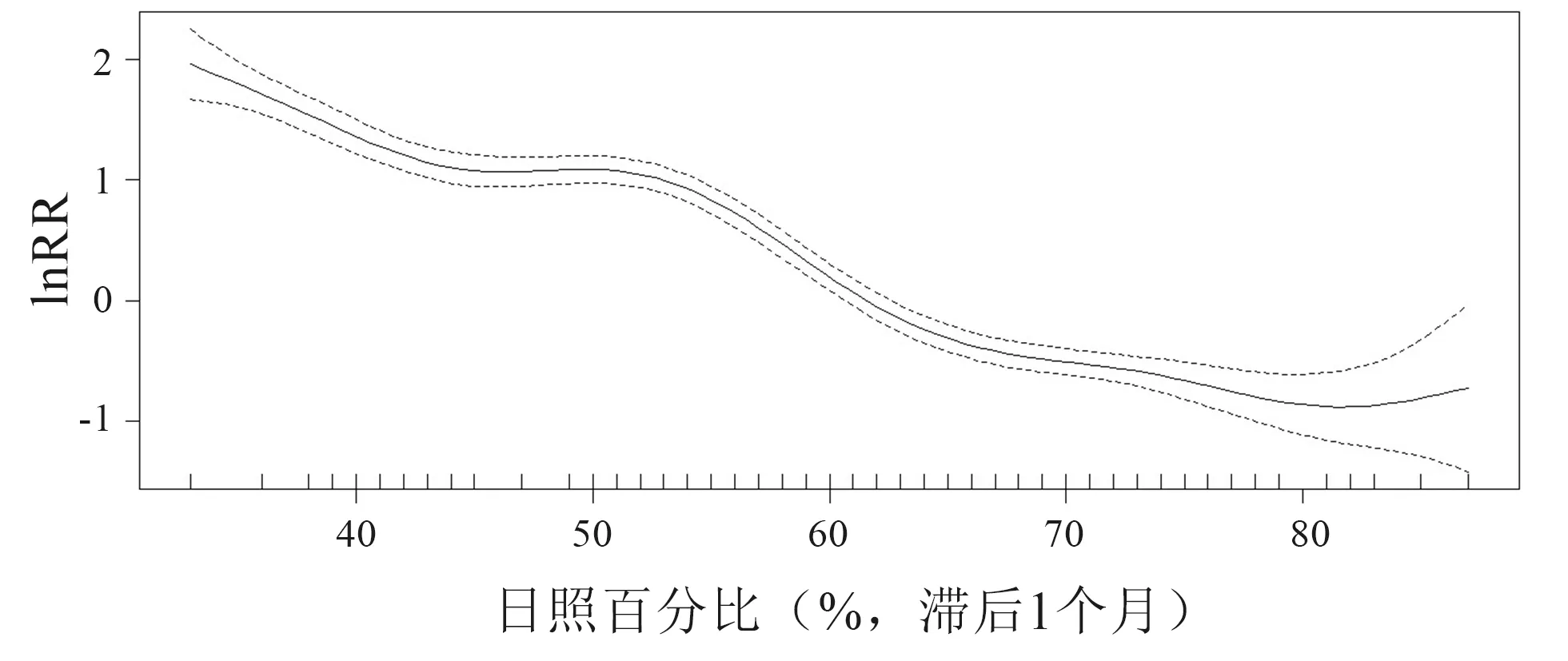
图7 基于月日照百分比的广义相加模型拟合曲线
6.多变量GAM模型
本研究所得的最终广义相加模型为:细菌性痢疾发病数=年份+平均最高气温的平滑函数+平均气压的平滑函数+降水≥0.1mm天数的平滑函数+平均水汽压的平滑函数+日照百分比的平滑函数,模型的调整决定系数为0.852,模型可以解释88%的变异,拟合效果好。变量“年”系数为-0.125,表明细菌性痢疾的发病率呈随年份下降的趋势。平均最高气温、平均气压、降水≥0.1 mm天数、平均水气压和日照百分比的估计自由度分别为3.222、5.829、1.002、6.749和7.381,详见表2。所有变量的P值均小于0.10。
讨 论
本研究发现,气象因素与细菌性痢疾的发生密切相关,大多数模型的决定系数均超过0.5。在辽宁省葫芦岛市2004-2018年间细菌性痢疾的发病率随着时间的推移呈下降趋势,但气象因素与细菌性痢疾之间的强相关性不会改变。
在所有协变量中,最高气温与细菌性痢疾发生之间的关联比最低气温更强,这一现象与肠道传染病监测中志贺氏菌阳性检出率的分布特征一致[9]。此外,气温可能通过对人群生活习惯的影响而影响传播途径和人群的易感性。本研究发现细菌性痢疾的发病与降水≥0.1 mm的天数有关,结果与Hines等人[10]和Chen等人[11]的发现一致;上述两项研究均提示强降水与菌痢的发生密切相关。此外,本研究发现水汽压与细菌性痢疾的发病高度相关,结果与Li等人基于中国哈尔滨和衢州两个城市数据的研究结果相一致[12]。
尽管本研究发现气象因素与细菌性痢疾发病率之间存在很强的关系,但本研究存在如下局限性。首先,本研究仅收集了月别的气象数据和发病数据,在本研究中气象因素与细菌性痢疾发生关联中所有的滞后时间都小于等于1个月,即气压、降水和日照存在一个月的滞后效应。而在数据的月别尺度下,并未发现温度和湿度的滞后效应,提示后续收集数据时,应该以周[13]或日[7,14]为时间单位收集发病数据和气象数据,以最大限度地探索气象因素和细菌性痢疾之间的关系。其次,本研究所在的区域为温带季风气候,相关研究结果无法外推至其他气候类型。温带季风气候在夏季炎热潮湿,各气象变量之间可能存在一定的交互作用[15]或多重共线性[16],由此可能会影响多元模型中的最终结果,后续将探究多重共线性对结果的作用途径和作用大小。最后,本研究仅分析了气象因素对细菌性痢疾发病的影响,在不同空气质量情况下,气象因素对细菌性痢疾发病的影响有无变化尚未探究[17]。后续将继续收集相关监测数据,完善预测预警体系。

