微生物组学关联分析方法和策略*

樊 哲 吕嘉丽 张 帅 谷冰冰 张 涛△

【提 要】 目的 微生物组研究中的典型数据是由操作分类单元(OTU)计数组成,这些数据具有零膨胀、过离散、偏态等特点,常常被研究者忽视。本文旨在介绍微生物组学数据关联分析方法,并提出相关研究策略。方法 根据微生物组学数据特点,本文拟从线性相关分析和非线性相关分析的角度,对近年来国内外研究者提出的微生物组学数据关联分析的统计分析方法展开讨论。结果 根据各方法的核心思想及优缺点,总结统计分析策略。结论 运用本文提出的统计分析策略,可有效识别微生物同其他研究指标间多种函数形式的关联。为探讨微生物对人体健康影响,研究微生物的作用机制提供线索。

近年来,随着高通量测序技术及统计分析方法的发展,微生物组学联合代谢组、蛋白组及其他组学的多组学关联研究已成为系统生物学研究新趋势[1]。从系统生物学角度来看,整合多个层面组学数据,构建多组学关联网络,能更充分理解各分子间的调控及因果关系,为探索疾病深层发生发展机制提供新思路。组学数据通常具有高维的特点,在探索分析的阶段,可以通过关联分析的统计方法,过滤出有统计学意义的变量,从而为后续的机制分析筛选出更小范围的目标变量。然而,目前多数研究在微生物组关联分析中往往忽视了微生物组学数据特点及各相关性分析方法的适用条件,导致研究结果产生偏差,出现关联结论与生物学结论不一致的问题[2-5]。本文拟对近年来国内外研究者提出的微生物组学关联分析方法进行介绍,并系统地总结各个方法的核心思想及优缺点,提出微生物组学数据关联分析的统计分析策略。

微生物组学数据特点

微生物组学数据通常来自16S测序或宏基因组测序。16S测序是在提取微生物DNA后,对微生物16S rRNA基因高变异区域进行聚合酶链式反应 (polymerase chain reaction,PCR) 扩增和测序。而宏基因组测序是对研究样本中全部微生物的总DNA进行高通量测序,并且宏基因组测序有更深的测序深度,能鉴定到种水平甚至菌株水平的微生物[6]。处理后的序列在一定的相似度水平上聚类为操作分类单元 (operational taxonomic units,OTU),通常将相似水平大于97%的OTU纳入后续生物信息学和统计学分析。

真实的微生物组学数据(如表1所示)具有以下几个特征:① 稀疏性:观测单位中,每一个OTU有部分观测值为零,也被称为零膨胀现象。② 非线性:微生物丰度与其他组学数据或临床指标存在多种多样的非线性关系,而不只是单一的线性相关。③ 高维特点:微生物组学数据还具有与其他组学数据相同的高维特点,即变量数大于或远大于样本数的情况。④ 过离散:OTU数据存在过离散的现象,即变量的方差大于均值。迄今为止,仍没有一种方法或策略能够应对微生物数据的众多挑战。

表1 微生物组学数据分布

微生物组学关联分析常用统计分析方法

微生物组学关联分析的研究目的通常包括:①从高维特征中过滤出少量特征用于后续机制研究。②构建多组学关联网络。传统的关联分析方法仅能发现两变量之间的单调关系,而微生物同其他水平分子之间可能存在多种函数形式的非线性关系。因此,根据研究目的和相关关系的形式,微生物组学相关性分析方法可分为以下几类:①传统关联分析方法:包括传统单变量相关统计方法及其用于微生物组数据的扩展方法,仅能检验出线性关系。②零膨胀模型:检验变量间的线性关系,更好地解决了微生物组数据偏态,零膨胀和过离散等问题。③基于互信息的方法:检验变量间的非线性关联关系,且无分布要求。④知识驱动的方法:构建关联网络。本研究对十种关联分析方法进行简要的介绍和比较(如表2所示)。

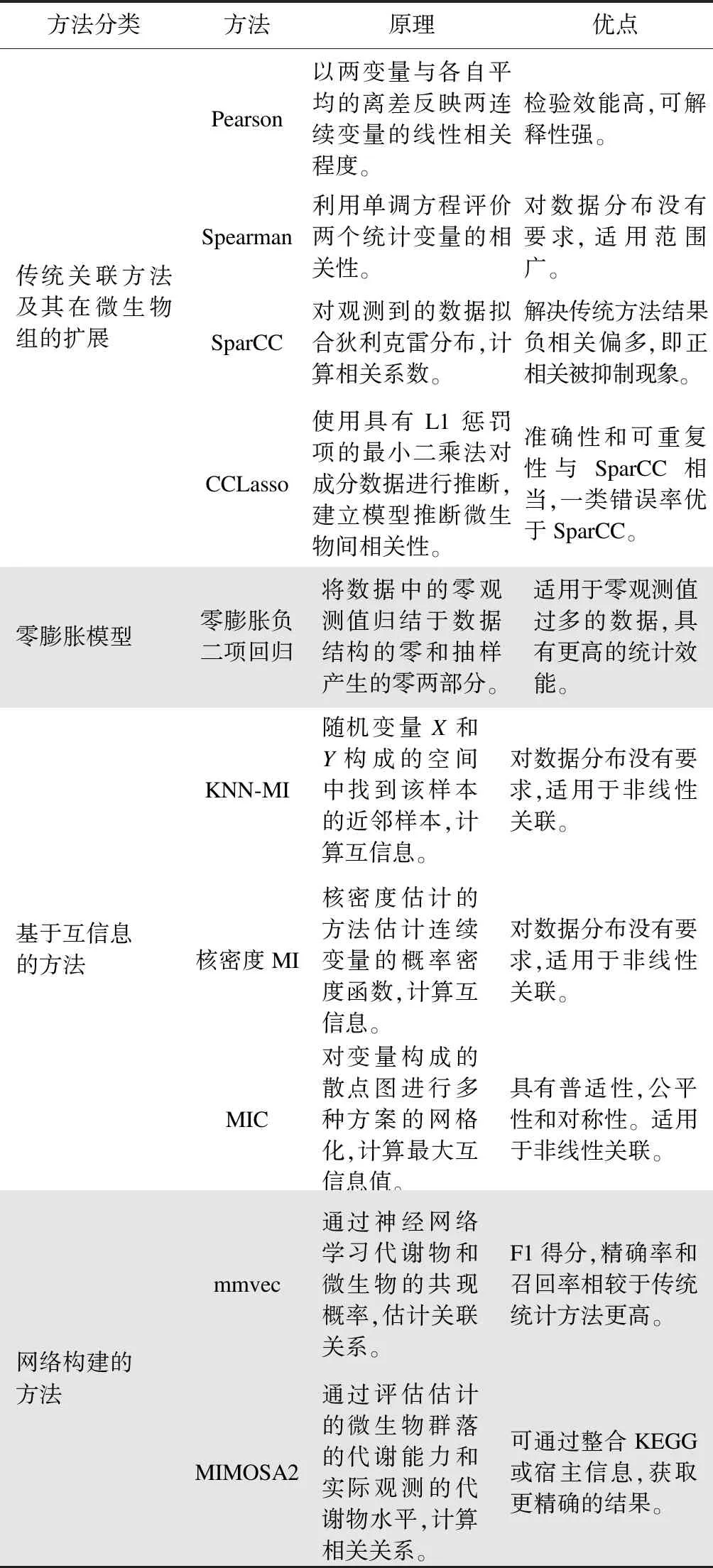
表2 关联分析方法原理及优点

1.传统关联分析方法及其扩展方法

线性相关分析因具有可解释性强的优势而经常被使用。Pearson相关以两变量与各自平均的离差反映两连续变量的线性相关程度[7]。该方法可以定量描述相关强度与方向,但当不满足正态性假设或样本量小于30时,难以得到可信结果。Mao等在山羊瘤胃微生物组的多组学研究中,应用单变量相关方法建立微生物的属与代谢物之间的Pearson相关矩阵,发现瘤胃微生物群落结构的改变与代谢物之间存在明显的相关性[8]。然而Pearson方法对变量分布要求严格,且微生物组数据通常呈现偏态或极偏态分布,不满足Pearson方法的使用条件,继续使用该方法可能导致检验效能下降,甚至出现错误的结果。

Friedman等在Pearson相关分析的基础上进行了改进,提出了成分数据稀疏关联(sparse correlations for compositional data,SparCC) 方法用于分析微生物成分数据,根据观测值的Dirichlet分布对关联程度进行估计[9]。微生物组中的成分数据即相对丰度数据,描述单个物种占整个样本微生物群落的百分比,某一样本内所有物种的相对丰度相加等于百分之百这一特点可能会导致传统的关联分析方法得到虚假的关联。基于lasso的成分数据关联方法(correlation inference for compositional data through lasso,CCLasso)也适用于微生物数据关联分析,其原理是在对成分数据进行对数转换后,使用基于惩罚函数的最小二乘法估计相关系数[10]。SparCC方法用于成分数据分析,解决了一般方法结果中正相关性被抑制的问题。You等人通过模拟研究发现,相较于Pearson方法,在微生物和代谢物关联分析时使用SparCC和CCLasso两种方法能更好地控制假阳性错误率[11]。这两种方法作为传统方法在微生物组学中的扩展,虽然解决了微生物组数据偏态的问题,但忽视了微生物组中数据的零膨胀特点,观测值中过多的零值可能导致这些方法性能下降。

Spearman秩相关分析适用于估计连续或有序变量间的单调关联研究,该方法对变量正态性不做要求,相比于Pearson相关其适用范围更广[12]。目前,Spearman秩相关分析在微生物组学领域中已被广泛用于识别微生物与其他水平分子或临床指标之间的关联性[13-15]。Spearman秩相关是一种非参数方法,适用范围比Pearson更广,但其中仍存在一些问题:(1)微生物数据中零观测值出现的概率通常远远超出一般计数模型(如泊松回归和负二项回归模型)的预期范围,如果继续使用一般关联分析方法可能得到错误结论。(2)Spearman秩相关方法作为一种非参数的方法,其统计检验效能较低。(3)只能识别具有单调性的相关关系,对于微生物关联研究中的多种函数关系的非线性相关不敏感。

2.零膨胀模型

Lambert首次建立了零膨胀泊松回归模型,它的基本思想是将计数数据中的零观测值归结于两部分,一是来源于数据结构的结构零,二是由分布产生的抽样零[16]。

零膨胀泊松回归模型可以看作Bernoulli分布和Poisson分布组成的混合分布,其概率密度函数为:

Xu等通过大量的模拟实验,比较了零膨胀模型与常用方法对具有零膨胀特征的数据进行建模的性能[17]。模拟研究表明,零膨胀模型可以较好控制一类错误率,并且具有更高的统计效能,对参数估计更准确。

然而,泊松回归模型假设事件发生的期望和方差相等,并且要求事件发生前后相互独立,但微生物数据方差通常大于均数,表现出过离散的现象,往往不符合这一假设,这将导致模型参数估计值的标准误偏小,参数Wald检验的假阳性率增加。为了解决零膨胀数据中的过度离散问题,Martin. Ridout研究了零膨胀负二项回归模型,并证明了零膨胀负二项回归比零膨胀泊松回归模型更适合处理离散度高的数据[18]。零膨胀负二项回归模型以负二项分布为基础,相比于零膨胀泊松回归模型,能更好拟合不同离散度的数据。Wu等使用零膨胀负二项回归模型发现表皮生长因子受体阳性的女性肠道菌群α多样性较低,随着乳腺癌恶化FirmicutesProteobacteria等微生物丰度增加[19]。Schwimmer等用同样的方法研究了非酒精性脂肪肝患者的肠道微生物,发现炎症相关菌群与非酒精性脂肪发病及其严重程度存在关联,Prevotella的丰度与肝纤维化有关,并且使用菌群构建了区分能力较好的判别模型[20]。

线性相关是容易解释的相关形式,针对微生物数据特点,零膨胀模型对于微生物数据线性关系的检验效能显著高于其他方法。但是,零膨胀模型在识别微生物和其他层面组学变量或一些临床指标间的复杂非线性关联中存在局限性。

3.基于互信息的关联分析方法

互信息 (mutual information,MI) 是来源于信息论中熵的概念,可用于度量两个随机变量之间依赖程度,表明一个随机变量包含关于另一个随机变量的信息量[21]。互信息的计算中,两个随机变量(X,Y)的联合分布为p(x,y),边缘分布为p(x),p(y),互信息I(X;Y)是联合分布p(x,y)于边缘分布p(x)p(y)的相对熵,即

根据熵的连锁规则,有

H(X,Y)=H(X)+H(Y|X)=H(Y)+H(X|Y)

互信息对样本的分布类型无特别要求,可以有效度量变量间线性关系和非线性关系,两个随机变量之间的互信息越大,则两者之间的相关性就越强。传统的互信息中要求变量是离散的且已知双变量的联合概率密度。微生物物种丰度是计数数据,可以先对微生物进行分箱,再计算互信息。然而传统互信息方法对于分箱的方式选择具有敏感性,不同的分箱方式可能导致结果差异较大。

Kraskov提出使用基于K近邻 (K-nearest neighbors,KNN) 的方法计算两连续变量的互信息[22]。该方法无需知道概率密度函数形式,避免了对概率密度函数的估计,适用于非线性不规则分布的数据。其基本思想是在由随机变量X和Y构成的空间中首先找到给定样本的k个近邻样本,再计算X和Y轴方向上距离小于K近邻距离的样本数目,并据此进行互信息估计。非参数方法除了K近邻方法还包括核密度估计的互信息[23]。K近邻和核密度估计方法将传统的互信息适用范围从离散变量扩展到连续变量。Jahagirdar等使用互信息方法构建了代谢物-代谢物的关联网络,并发现互信息方法与Pearson和Spearman方法分析的结果存在差异[24]。Numata等使用基于KNN的互信息方法分析拟南芥代谢物浓度数据,发现互信息能够检测出Pearson相关系数无法发现的额外非线性相关[25]。K近邻和核密度估计的互信息的缺点在于没有合适的归一化数据预处理方法,关联强度大小不便于比较。

David N. Reshef在互信息方法的基础上提出了最大信息系数 (maximal information coefficient,MIC) 的方法[26]。MIC方法首先对变量X和Y构成的散点图进行网格化,并且求出不同网格化方案中的最大互信息值,再对最大的互信息值进行归一化。MIC的计算方式如下:

Logares等将MIC方法用于分析海洋表层微生物,发现原核生物和海洋的温度与氧气有关[27]。Cao等提出了一种共表达网络分析方法,即在加权基因共表达网络分析 (weighted correlation network analysis,WGCNA) 的基础上,结合了Pearson相关系数和最大信息系数作为配对基因之间的相似性度量,以此构建共表达网络。该方法能发现WGCNA方法所忽略的非线性相关,识别更多潜在的包含癌症信息的基因,具有更高的预测精度[28]。MIC的优点是可用于各种函数形式的相关关系分析,在样本量足够大时能为不同类型单噪声程度相似的相关关系给出相近系数。但MIC的缺点在于其统计效能较低,在进行大规模的探索分析时,需要较大的样本量。

4.知识驱动的网络构建方法

Rob Knight提出了microbe-metabolite vectors (mmvec) 神经元网络方法,该方法专用于微生物组与代谢组数据,通过学习代谢物和微生物共现概率,确定微生物与代谢物之间的关系[29]。Mmvec方法通过给定单个输入微生物序列的情况下估计代谢物响应强度,通过计算估计关联与真实关联的误差对模型的权重进行调整,并进行内部交叉验证和迭代训练,预测微生物和代谢物的关联关系。Mmvec相比于Pearson,Spearman和SparCC具有更高的F1得分,精确率和召回率。

Borenstein Lab提出了MIMOSA2模型,基于微生物在全基因组代谢模型(genome-scale metabolic models,GEMs)或KEGG中已知的代谢相关信息,计算微生物群落代谢能力 (community-wide metabolite potential,CMP)构建代谢模型来估计群落组成对代谢物浓度的影响,并评估CMP与观测到的代谢组特征的差异,从而发现相关的微生物和代谢物[30-32]。然而mmvec和MIMOSA2方法的适用范围较小,仅能用于微生物和代谢物的关联分析,从多组学的角度来看,微生物可能同其他多个水平的分子之间存在关联甚至因果调控关系。

微生物组学关联分析策略

多组学研究设计在成为探索疾病发生发展深层机制的有力手段的同时,也为统计分析带来了新的机遇与挑战。研究者们在进行微生物组学数据关联分析过程中,常常忽略微生物组学数据零膨胀,过离散等数据特点,以及相应统计分析方法原理与前提假设,导致采用单一分析方法可能存在检验效能过低的问题,甚至出现错误结果。本文综合上述分析方法特点及微生物组学数据特点,探索了微生物组学关联分析策略(流程图如图1所示),具体总结如下:

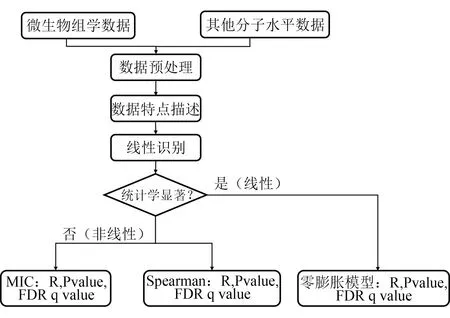
图1 微生物组学数据关联分析策略流程图

1.数据预处理。参数方法对数据分布有严格要求,根据使用的方法对数据进行相应预处理是十分必要的。对于微生物成分数据,需要进行中心对数转换:

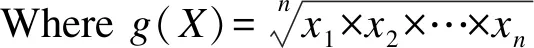
其他水平分子和临床指标等一般的连续变量也建议进行处理(如标准化,对数比转换,BOX-COX变换等),使变量分布为标准正态或近似标准正态分布。

2.数据特点描述:对原始的和预处理后的数据进行描述性统计分析,关注变量分布情况。此外,还应描述微生物组中每个变量零观测值比例,对零观测值比例较高的变量,应采用零膨胀模型和非参数的关联分析方法。

3.线性关系识别。针对微生物数据特点,零膨胀模型对于微生物数据线性关系的检验效能显著高于其他方法,并且一类错误率较低。同时,线性相关形式相较于非线性相关形式具有更好的生物可解释性。使用零膨胀负二项回归或零膨胀beta回归模型(分别适用于微生物绝对丰度数据和相对丰度数据)对数据进行模型拟合,根据回归系数的大小以及回归系数的显著性得到两个变量间的(偏)相关系数大小及统计检验显著性,若相关系数检验的P值小于设定置信水平α,则认为两变量间存在线性相关,否则按照存在非线性关联进行进一步检验。

4.关联分析。对上一步识别为线性相关的变量对,采用零膨胀模型估计相关关系强弱。对于不存在线性关系的变量对,可以通过非线性相关分析方法做进一步探索。MIC可以发现多种多样的相关函数形式,Spearman相关分析方法虽然统计检验效能高于MIC,但只能发现存在单调关系的变量。因此可同时采用MIC和Spearman的方法分别进行非线性相关关系识别,计算变量间的最大信息系数和相关系数,并给出系数检验的P值,若P值小于置信水平α,则认为两变量间存在非线性相关。最后,给出线性和非线性相关的R和P值。

5.多重假设检验问题处理。高维情境常涉及多重检验问题,传统的统计检验方法中会产生大量假阳性结果,大大增加假阳性错误[33]。对于多重检验,在检验水平固定的情况下,随着检验次数的增加,至少犯一次假阳性错误的概率将会趋于1。因此需要考虑对假设检验结果的P值进行校正,将校正后的P值控制在某一固定水平及以下。目前常用校正方法包括Bonferroni校正法及FDR校正法[34]。对于第二步和第三步过程中的多重假设检验问题,采用FDR的方法校正P值的阈值。

由于微生物组学数据的复杂特性,上述分析手段能在一定程度上解决组学数据统计分析问题,但仍存在局限性。由于各变量间存在多种非线性关系,实际分析中可能需要结合多种网络构建方法[35]。基于互信息的方法虽然适用于多种非线性关系并对数据分布没有要求,但是在小样本条件下检验效能较低,如何提高关联分析方法适用范围和检验效能需要进一步研究。此外,横断面研究对于探索微生物与其他水平分子的调控及因果关系可能存在证据不充分的问题,纵向研究中的研究策略和研究方法需要进一步探讨。以上三个关键科学问题的解决将会对微生物组学关联分析提供新的思路与契机。