冷轧板形数字孪生模型与协调优化信息物理系统

张殿华，魏臻，王军生，宋君，王青龙，孙杰

（1.东北大学轧制技术及连轧自动化国家重点实验室，辽宁 沈阳 110819；2.鞍钢集团北京研究院有限公司，北京 102211）

近年来，随着传统轧制生产逐步向数字化转型升级，对板形质量的要求也越来越高，如何快速有效的进行高品质冷轧带钢生产是眼下面临的一大问题。未来钢铁行业重大战略方向是利用基于数字孪生的信息物理系统（Cyber-Physical System，简称CPS）智能化关键技术，实现全流程、多工序、系统级和全局级的钢铁生产过程优化控制，以提升产品质量和生产效率［1］。将生产数据与专家知识融合，采用数字感知技术，旨在解开冷轧板生产过程中的“黑箱”，建立冷轧板形控制信息物理系统，进而将生产过程以透明的姿态和数字模型的方式呈现出来。这种方式保证了模型精度的提升，使人们对生产过程的认知更加深入，还为新型板形控制功能的实现提供了重要支撑［2-3］。

在工业控制领域，板带连轧是最复杂的控制过程，板形控制过程具有非线性、遗传性、强耦合等特征，现有的数学模型不能充分描述这些关系［4-5］；另外，目前蕴含在钢铁大数据中的价值没有得到充分挖掘，在由“数据”到“信息”的处理过程中存在断层，没有形成对板形控制的良好反馈［6-7］。为提高实际板形控制水平，本文在轧制机理认知的基础上，与生产数据的感知有机融合，解析了板形调节机构与板形变化的关系，构建了以数字孪生模型为核心、以多目标协调优化为特征的板形控制信息物理系统，实现了冷连轧多机架工艺参数动态优化设定。

1 数字化板形控制架构

以某1420 mm冷连轧轧机为例，该五机架出口的板形检测辊分为38个测量段，152个测量变量；此外控制系统还有轧制力、轧制速度、带钢温度分布等其他输入变量。该轧机的板形执行机构主要有轧辊倾斜 （Roll Tilting，RT）、工作辊弯辊（WorkRollBending，WRB）、中间辊弯辊（Intermediate Roll Bending，IRB）、中间辊横移（Intermediate Roll Shifting，IRS）、工作辊横移以及工作辊分段冷却。这些控制变量使得板形控制系统成为一个典型的多变量输入输出和强耦合的非线性控制系统［8］。板形控制信息物理系统CPS工作模式如图1所示，该工作模式分为内外两环，内环针对高精度设定计算，将设定计算所需实时数据无滞后地反馈给在线动态设定控制系统，进行高精度、短周期的高精度实时动态设定；外环针对高精度模型自学习，将相关大数据信息反馈给数字感知模型学习系统，进行模型自学习、自适应，强化系统自治功能，实现模型参数的高精度自学习，最终目标是使数字孪生模型与实际系统高度 吻合，从而实现极高的控制精度。

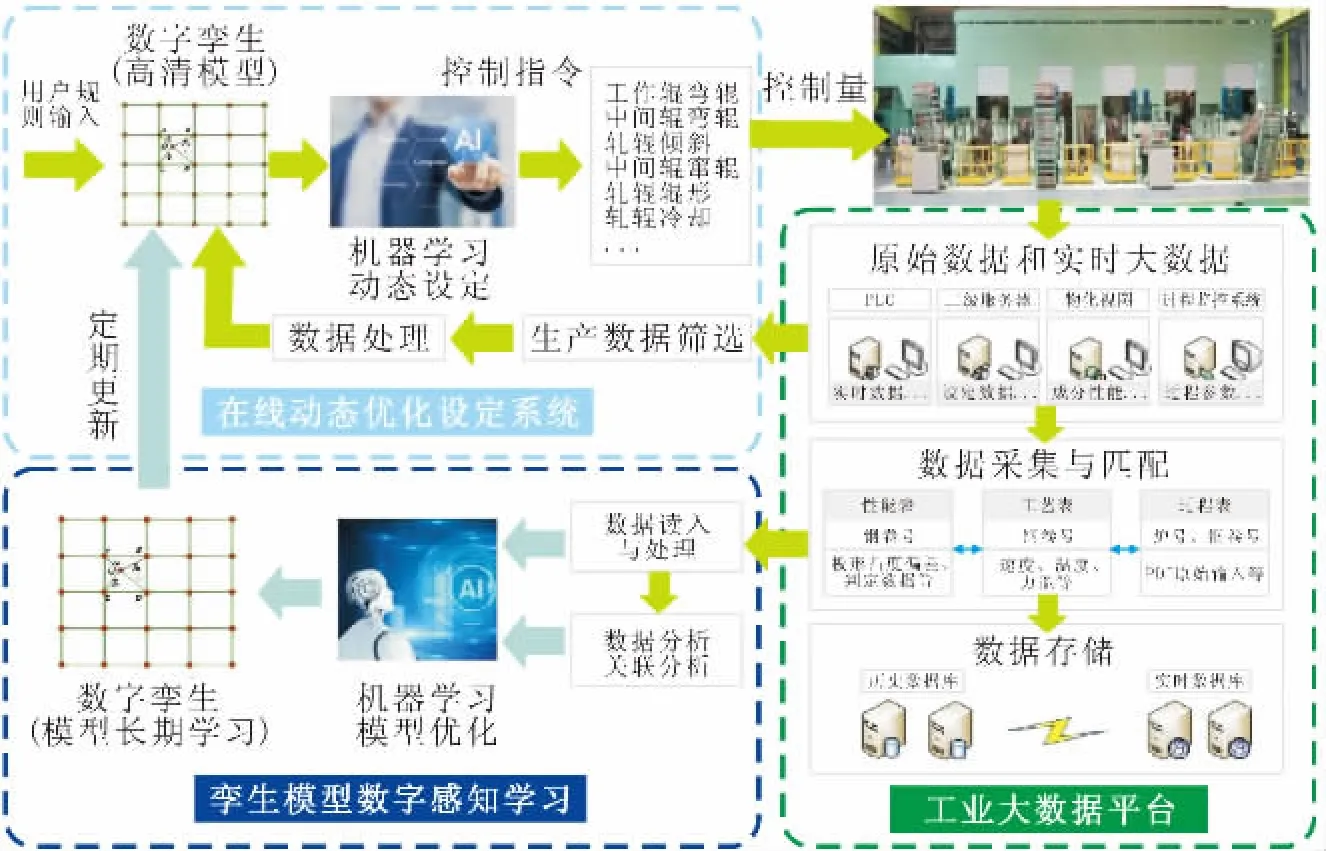
图1 板形控制信息物理系统工作模式Fig.1 Working Mode for Cyber-physical System of Cold-rolled Strip Flatness Control

2 板形数字孪生模型

数字孪生系统是CPS的核心支撑，具备足够高的精度才能承担优化控制的任务［9］。现代先进的六辊冷轧机多具备多种板形调节手段［10］。图2中展示的调控功效系数综合考虑了单个执行机构对板形控制所产生的综合效果。基于调控功效的板形控制算法直接针对板形偏差分布进行控制，跳出了传统对板形偏差信号进行一次、二次或四次识别的框架［11-13］。板形调控功效系数定义为在一种板形调节机构的单位调节量作用下，轧机的承载辊缝形状沿宽向各处的变化量。

式中，i为轧辊轴向离散点，yi为离散点i处的宽向坐标；Ei，j（yi）为第 j种板形调节机构在宽度 yi处的板形调控功效系数；Δuj为第j种板形执行机构的调节量；Δgi（yi）为第 j种板形执行机构在调节量Δuj作用下坐标yi处承载辊缝的变化量。

通过将控制段与测量段一一对应，每个控制作用（或执行机构）对所有段的板形都有影响，影响越大，效率系数越大，因此可以实现对冷轧板形的精细控制，而控制效果与功效系数矩阵的准确性密切相关［14］。

2.1 轧制过程数据治理

冷轧生产数据具有大噪声、强耦合、高通量的特点，难以直接用于精确求解功效系数［15］，必须在使用中进行数据治理，即降噪解耦。通过对信号降噪方法的原理进行深入研究，在原有降噪方法基础上加以改进，提出了一种融合集成经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）和小波变换（Wavelet Transform，WT）的数据治理方法。

集成经验模态分解具有出色的信噪比和优秀的时频聚焦性能，非常适用于分析非线性、非平稳的信号序列［16-17］。其优点在于无需依赖预定义的基函数，自适应地将信号分解成多个本征模态函数 （Intrinsic Mode Function,IMF），IMF 的频率从高到低逐渐展现。引入极小幅度的高斯白噪声信号后再进行分解，可以在不同尺度上得到连续的解，从而有效地解决了模态混叠导致分量不准确的问题，由于高斯白噪声的零均值的特点，经过多次分解后进行均值处理可以消除，并不会影响原始信号的准确性。引入小波变换法对前几组IMF进行信号处理，尽可能地保留住有用信息［18］。采用连续均方误差的方法（CMSE）分别计算相邻IMF分量的均方误差，从而寻找噪声主导的模态分量和有用信息主导的模态分量的分界点k，将其定义第一个噪声能量最低值点，这样可以更准确地区分噪声和有用信息的模态分量［19］。

式中，N为数据样本的数量；C为本征模态函数总数。

图3 EEMD-WT算法流程图展示了EEMDWT降噪过程。舍弃仅包含噪声的模态分量，基于CMES得到合适的k值后，使用WT对高频IMF分量进行降噪处理。再将处理后的高频IMF分量与其他低频IMF分量重构，完成数据降噪治理。

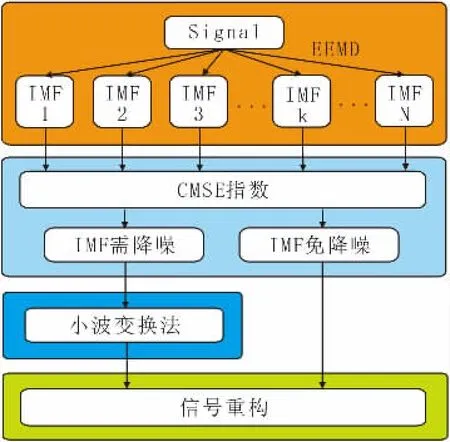
图3 EEMD-WT算法流程图Fig.3 Flow Chart for EEMD-WT Algorithm

在图4中，将EEMD-WT方法与典型的SVD（奇异值分解）降噪法和均值降噪法进行对比。结果显示，虽然三种方法都能还原出数据的趋势，但在细节方面，EEMD-WT方法能更好地提取有效信息，还原出原始仿真数据。EEMD-WT降噪方法的信噪比为24.94 dB，优于SVD降噪方法的22.19 dB和均值降噪方法的20.10 dB。证实了EEMD-WT降噪方法的准确性和优越性。

2.2 基于OSC-PLS算法获取调控功效系数

通过数据驱动算法获取板形调控功效系数是有效手段。主成分分析法 （Principal Component Analysis，PCA）和偏最小二乘算法 （Partial Least Squares，PLS）是数据驱动方法中最典型的一类算法，它们通过降低含有多个耦合变量和大量噪声干扰的工业数据的维度，来减弱变量间的强耦合关系，进而高效地提取数据中研究者所关心的主要信息［20］。与主成分分析算法相比，PLS算法同时对自变量与因变量提取主成分（T和U），在使二者相关程度达到最大的前提下，最大程度包含各自数据集中的变异信息。而正交信号校正法（Orthogonal Signal Correction，OSC）可以将自变量中与因变量不相关的信息滤除掉［21］。采用OSC与PLS回归相结合的算法，即正交信号校正法改进的偏最小二乘算法（OSC-PLS 算法）［22］，可以减小自变量X中的扰动信息。

本研究主要以工作辊弯辊、中间辊弯辊和轧辊倾斜为研究对象，计算获取三者的调控功效系数。首先利用商业有限元软件ANSYS，基于弹塑性有限元法建立耦合带材与轧辊变形的高精度三维数值仿真模型［23-24］，针对不同轧机配置，建模过程所采用的轧机几何参数完全参照实际生产轧机的机械设备数据。基于三维有限元模型，模拟计算了不同工况下的带材轧制过程，根据带材横向厚度分布曲线可计算出带材中心凸度C40、局部凸度C300和边部减薄E40以及比例凸度的变化情况，根据板形与凸度之间的转换关系［25］，用带钢纵向纤维的相对延伸差的变化量（平直度，IU）表示轧机承载辊缝的变化量，因此板形调控功效系数可以由式（4）计算：

式中，F为板形偏差分布；ΔF为板形偏差变化量。

通过有限元仿真获得不同板形调节机构投入时轧后带钢纵向纤维条长度差数据，可计算获取工作辊弯辊、中间辊弯辊和中间辊横移的调控功效系数曲线作为先验值。根据降噪后的训练数据分别采用PCA和OSC-PLS算法建立工艺参数变化量和板形值变化量的回归预测模型，将回归模型中的系数矩阵按照与自变量工艺参数矩阵中执行机构调节变化量相对应进行分块，并从分块系数矩阵中获取各板形执行机构的调控功效系数，并与经验法获得的结果进行对比，如图5所示。

图5 根据PCA、OSC-PLS以及经验法获取的板形调控功效系数曲线Fig.5 Curves of Efficiency Coefficients Control of Flatness or Shape Obtained by OSC-PLS,PCA and Experiential Method

图6为根据3种不同算法获取的调控功效系数对应的板形计算误差云图。对比结果可知，基于OSC-PLS算法获取的调控功效系数计算出的板形误差变化范围很小；PCA算法次之；经验法对应的板形计算误差最大，且变化范围也很大，且最大值远小于PCA算法和经验法。因此，对于OSC-PLS、PCA和经验法3种方法而言，通过OSC-PLS算法获取的调控功效系数更能准确描述实际数据中板形变化量与执行机构调节变化量的比例关系。

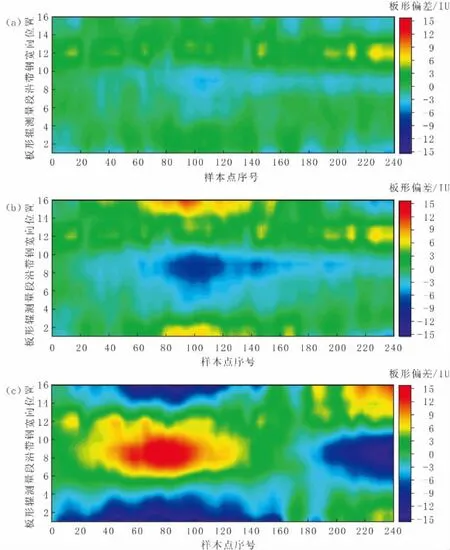
图6 基于不同算法获取的调控功效系数对应的板形计算误差云图Fig.6 Cloud Atlas for Calculation Errors of Flatness or Shape Corresponding with Efficiency Coefficients for Control of Flatness or Shap Obtained Based on Different Algorithms

3 板形控制信息物理系统

通过对轧制过程数据的治理与高精度板形调控功效系数的获取，建立起了与六辊轧机实体系统相互映射的虚拟镜像，由此实现了板形数字孪生模型的构建，作为虚拟（Cyber）部分，与UCM轧机及板形执行机构的代表的实体（Physical）部分，组成了冷轧板形控制信息物理系统，如图7所示。冷轧板形控制信息物理系统通过在虚拟的三维数字空间计算板形执行机构与板形间的控制协调关系，把实测数据传输到数字空间对应的数字孪生体，通过多目标智能优化算法来实现板形的闭环精准控制， 并通过虚拟仿真使控制过程和结果可视化［26］。

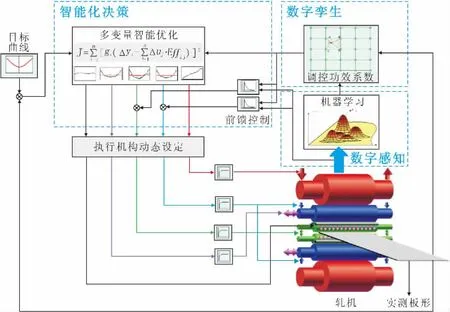
图7 冷轧板形控制信息物理系统Fig.7 Cyber-physical System of Cold-rolled Strip Flatness Control

3.1 基于深度神经网络算法的板形预测

高精度的预设定模型可以保证带钢进入稳定轧制前的板形质量，缩短板形调节时间，对整个板形控制过程具有重要意义［27-29］。数据驱动的方法可以综合分析预设定控制时生产现场大量其它工艺参数对板形的影响，建立板形预测模型，并以板形预测模型为基础，结合优化算法进行板形优化设定，可以排除其它工艺参数带来的干扰。

采用智能算法 KPLS［30］与 DNN［31］分别建立板形预测模型。数据预处理之后数据集共计1 829个离散样本点，样本点中含有轧制速度、轧制力、工作辊弯辊力、中间辊弯辊力、轧辊倾斜量、轧制张力等68个工艺参数变量与20个板形值变量。以8：2的比例对数据进行划分，分别用于预测模型的训练与测试。KPLS模型的均方根误差为0.274 6，DNN模型的均方根误差为0.167 8，结果表明，DNN模型具有更好的预测性能。图8是测试集各样本点的板形预测值均值和真实值均值的误差散点分布图。从整体板形的角度来看，DNN预测模型89.25%的样本点的整体预测误差小于1 IU，而KPLS预测模型仅有73.94%的样本点的整体预测误差小于1 IU。

图8 模型的预测性能对比Fig.8 Comparison of Predictive Performance by Models

图9是针对测试集中每个样本各处板形测量点的预测值与真实值的误差统计，能从更细节的方面比较两种模型的预测性能。测试集共387个样本，DNN预测模型中预测误差小于1 IU的测量点数为276，显著高于KPLS模型的结果（227）。以0.1 IU为区间，绘制模型预测误差在0～1 IU的各小区间的百分比占比情况。DNN预测模型中预测误差小于1 IU的测量点数总占比高于KPLS模型，同时，误差小于0.5 IU的测量点各区间占比均高于KPLS模型。

图9 模型的预测误差对比Fig.9 Comparison of Predictive Errors by Models

3.2 基于智能预测模型的板形设定优化

由于轧辊横移响应速度过于缓慢同时调整过程易划伤带钢表面，因此通常在带钢轧制前就已固定横移量大小，在轧制过程中不再进行更改［32］。本研究的板形预设定控制主要针对的是WRB、IRB以及RT，采用梯度下降法结合上文中建立的DNN板形预测模型进行板形的优化设定，但由于DNN预测模型的梯度过于复杂，无法直接求出，用差分方法近似计算出目标函数的梯度，具体计算步骤如下：

（1）取任意一个样本点，通过DNN预测模型计算得到该样本点的板形预测值F1。

（2）对该样本点的第一个变量加上足够小的数ε，计算得到变化后的板形预测值F2,本文中ε取0.000 1。

（3）变化后的板形预测值与初始的板形预测值的平方和之差除以ε，即为第一个变量所对应的梯度值T1。

（4）重复步骤（1）～（3），即可得到所有变量所对应的梯度值，从而完成DNN板形预测板形梯度的计算。

板形的优化设定过程如图10所示，其中，Δ、Δ'、Δ''分别代表对轧辊倾斜量、工作辊弯辊力、中间辊弯辊力调整后得到的板形偏差。

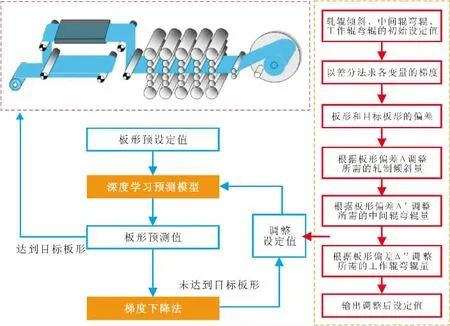
图10 板形的优化设定过程Fig.10 Flatness Presetting Process by Optimization

图11为基于DNN预测模型进行WRB、IRB和RT设定值优化前后的板形偏差云图。经设定值优化后的板形相较优化前有明显提升，板形标准差由优化前的3.42 IU降至1.91 IU。

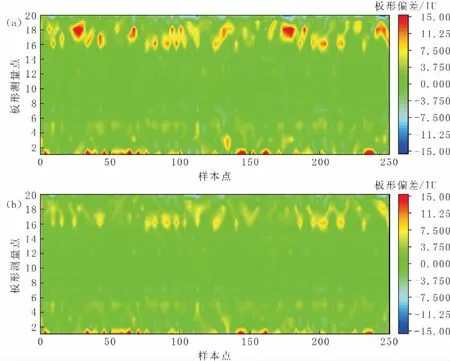
图11 基于DNN预测模型进行WRB、IRB和RT设定值优化前后的板形偏差云图Fig.11 Cloud Atlas for Flatness or Shape Deviation before and after Optimization of Setting Values for WRB,IRB and RT by DNN Prediction Model

为了更直观的分析板形设定优化对各设定量的调整效果，选择了测试集中第9号样本点和第181号样本点进行具体分析。图12和图13分别是第9号样本点和第181号样本点经过DNN模型优化后板形调控参数设定值变化，可以看出优化模型对两个样本点的工作辊弯辊力、中间辊弯辊力和轧辊倾斜设定值都进行了一定范围的调整。对优化前后的板形值进行对比可知，9号样本点优化前的板形标准差为4.31 IU，优化全部机架后的板形标准差为1.68 IU，181号样本点优化前的板形标准差为3.52 IU，优化全部机架后的板形标准差为1.82 IU，均有显著的优化效果。

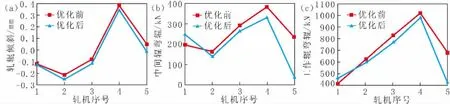
图12 9号样本点的调控参数Fig.12 Adjustment Parameters for No.9 Sample Position

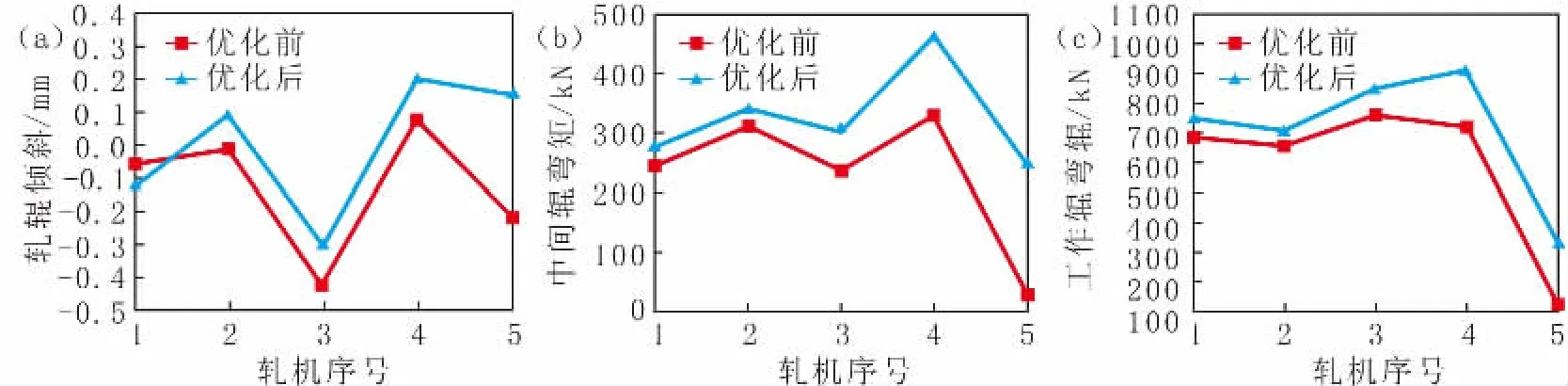
图13 181号样本点的调控参数Fig.13 Adjustment Parameters for No.181 Sample Position

4 结论

本文设计了数字化板形控制架构，提出了数据驱动的板形调控功效系数数字孪生模型构建方法，融合多目标优化方法，形成了板形控制信息物理系统。

（1）提出了EEMD-WT降噪方法，通过准确提取有效信息还原出原始仿真数据。同时，采用OSC-PLS方法建立了工艺参数变化量与板形偏差变化量之间的关系，提出了一种基于数据驱动的板形调控功效系数获取方法；

（2）构建了板形控制系统的物理模型，基于DNN算法实现了冷轧板形的精准预测。在此基础上，利用梯度下降法对板形控制工艺参数进行设定优化，成功将板形标准差从优化前的3.42 IU降低至1.91 IU。