用SCAD惩罚研究带遗传约束的Cox模型
管 锋, 晏海青
(1.郑州大学 数学与统计学院,河南 郑州 450001;2.光辉学校,河南 光山 465450;3.中国人民银行罗山县支行,河南 罗山 464299)
生存分析是对生存数据进行统计分析的一门新兴学科, 在医学、生命科学和可靠性工程等领域都有广泛应用.Cox比例风险模型是由Cox在1972年提出, 是生存分析中应用最多的模型[1].该模型是一个半参数模型, 不仅能应用于完整的观测数据, 而且对于带有删失的数据同样适用. 1975年Cox提出了偏似然的估计方法[2]来估计模型中的参数. 由于这种方法估计的结果不具有稀疏性, 一些常用的变量选择方法, 如最佳子集选择法, 逐步选择、计算量大且缺乏稳定性. Zhang等[3]将自适应LASSO估计方法应用到Cox比例风险模型中, 得到的估计量具有良好的Oracle性质. Yang等[4]研究了超高维Cox可加模型的特征筛选, 并且通过Monte Carlo模拟和实例分析检验了其可行性, 对Cox可加模型的应用给予了理论支持.
在生物等研究领域中, 一些变量间的交互作用对响应变量也有影响. 自适应LASSO的方法研究了带遗传约束的Cox模型, SCAD惩罚估计可以减少估计偏差并且估计量同时满足无偏性、稀疏性和连续性[5].因此自适应LASSO方法研究带遗传约束的Cox模型[6]的基础上,用SCAD惩罚估计方法研究带遗传约束的Cox模型也具有重要意义.
1 模型与方法
根据Fan等[7]在2001年提出来的惩罚似然的变量选择问题和线性回归模型中带交互项的变量选择问题, 给出带遗传约束的Cox模型, 并得到满足遗传约束条件的目标函数. 运用梯度下降法的思想并结合CCCP算法[8]得到新的参数估计算法.
1.1 模型提出
假设在一次生存研究中有n个相互独立的个体, 第i个个体观测到的生存时间为Ti,i=1,…,n, 是独立同分布的随机变量, 令Yi(t)=I(Ti≥t), 用来表示第i个个体在t时刻的生存情况.X(i)=(Xi1,Xi2,…,Xip)τ,i=1,…,n, 表示第i个个体对应的p维协变量;β= (β1,β1,…,βp)τ表示p维未知参数向量,Z(i)=(Xi1,…,Xip,(Xi1Xi2),…,(Xi,p-1Xip))τ, 表示含有交互项的协变量,α=(α12,…,αp-1,p)τ, 表示交互项的未知参数向量, 则带交互项的Cox模型可写成
(1)
在有右删失数据的情况下可以得到偏对数似然函数
(2)
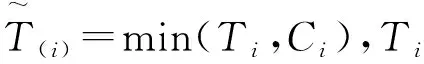
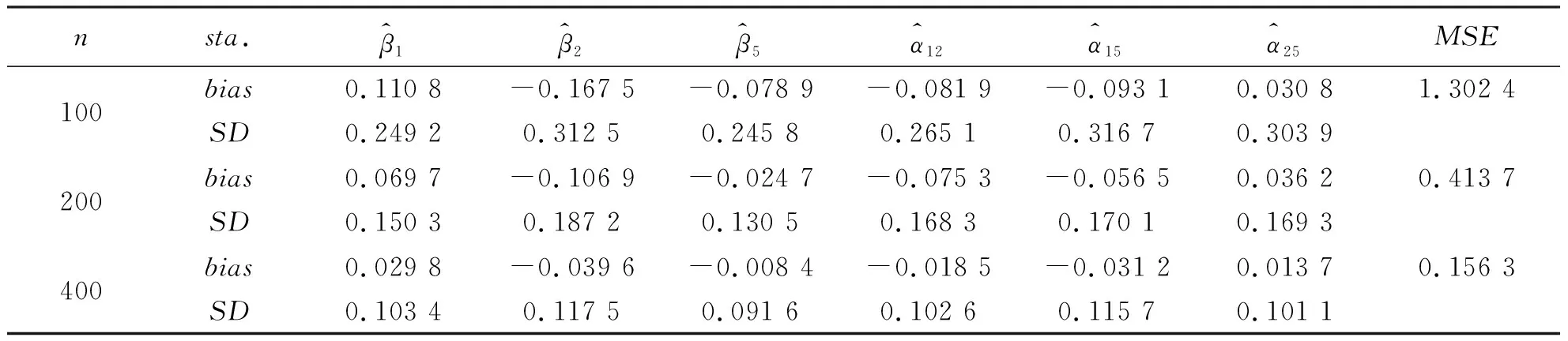
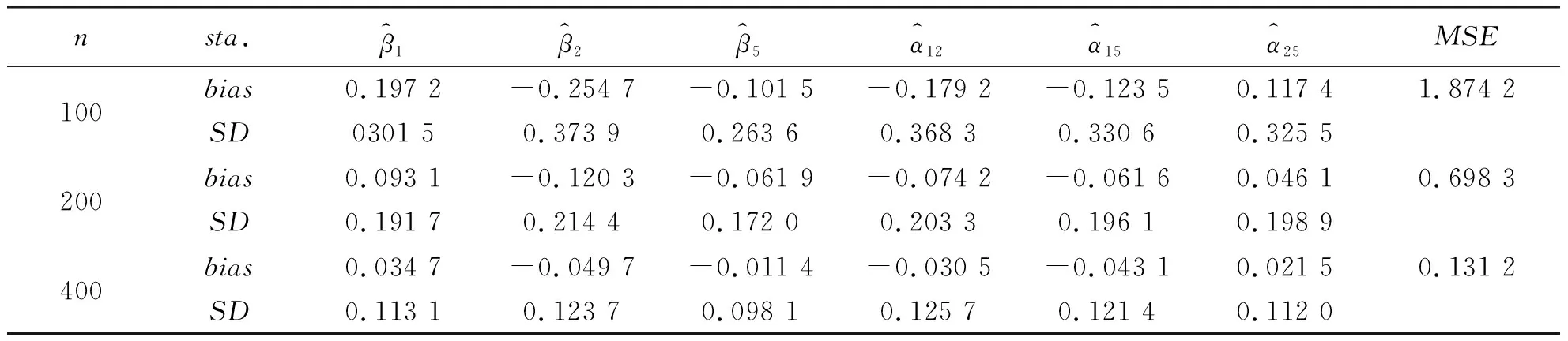
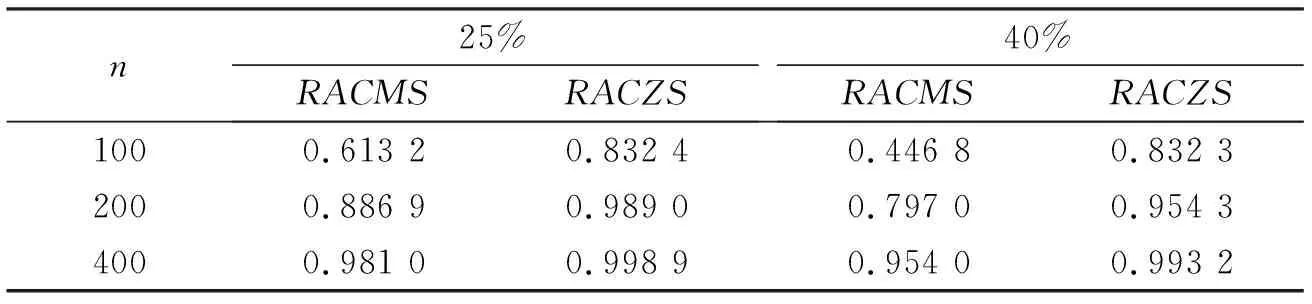
为了使估计量满足遗传约束条件, 重新参数化交互项的系数, 令αjk=γjkβjβk,j (3) 这里通过对交互项参数的重新参数化, 使得当βj=0或者βk=0时, 必有含变量Xj或者Xk的交互项系数为零.应用SCAD惩罚偏对数似然来估计参数, 不仅可以选择出主要项和交互项中对响应变量有解释作用的协变量, 而且还可以使得估计量具有Oracle性质, 同时满足遗传约束条件. (4) (5) (6) 其中θ*=(β*τ,α*τ)τ.通过最小化(5)式, 可以得到(4)式的最小解. 同理当γjk固定时, 目标函数可写为 (7) (8) (9) 通过最小化 (9) 式, 可以得到 (7) 式的最小解.上述估计过程的具体算法如下: 惩罚参数λβ和λγ的选择可参考文献[9]. 其中,j,k,l=1,…,p,k 性质1的证明类似Fan and Li (2001)中定理1的证明可得,这里省略. 假设真实的模型参数为 θ=(1,-2,0,0,-0.2,-2,0,0,-0.2,0,0,0.4,0,0,0)τ, 其中前五项为主要项Xi1,…,Xi5, 后十项为交互项Xi1Xi2,…,Xi4Xi5.主要项服从均值为0向量的多元正态分布, 协方差满足Cov(Xik,Xij)=0.5∣k-j∣,1≤k,j≤5,1≤i≤n, 交互项为对应主要项的乘积.由于在实践中得到的数据是删失的, 所以根据Bender[10]提供的产生生存时间的方法模拟生成随机右删失生存时间数据, 删失时间分布渐近服从U[0,c],c由删失率确定, 主要是研究n=100,200,400, 删失率为 25%和 40%的有限样本表现. 表1是在删失率为25%, 样本量分别为100, 200和400的情况下重复估计500 次得到的偏差, 标准差和均方误差.表2是在删失率为40%情况下估计的结果, 与表1对比可以发现, 在删失率增加的情况下估计的精确度随之减小, 随着样本量的增加, 估计的精确度也明显增加, 与渐近无偏估计的理论结果相吻合.表3结果是在不同删失比率和不同样本量下对正确选择出模型的评估, 从表中数据可以看出样本量越大删失率越小, 正确选出模型的概率越高. 表1 在25%删失率下非零系数估计的bias, SD和MSE 表2 在40%删失率下非零系数估计的bias, SD和MSE 表3 在不同删失率下模型和零系数的正选率 主要用SCAD惩罚估计方法研究带遗传约束的Cox比例风险模型的变量选择与参数估计问题, 利用SCAD惩罚估计方法对参数向量进行惩罚, 在给定的正则条件下估计量具有Oracle性质.另外, 在许多实际问题中, 主要项可能还不足以预测协变量和响应变量之间的关系,而该研究方法可以解决这类问题.1.2 算法实现
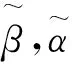
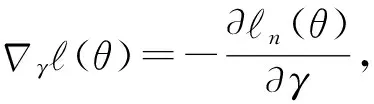
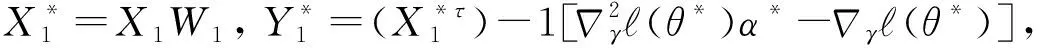
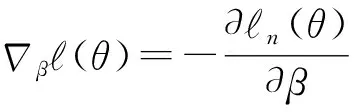
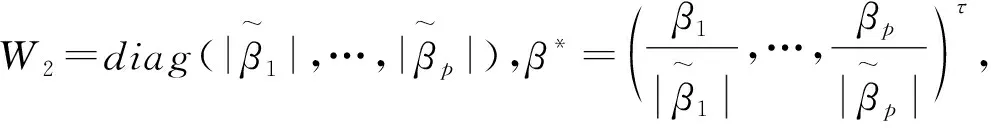
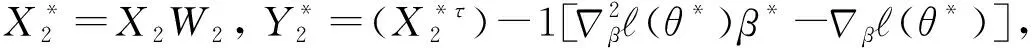
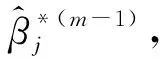
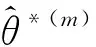
2 渐近性质
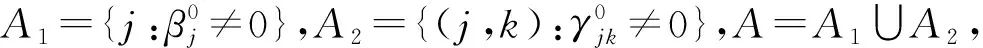
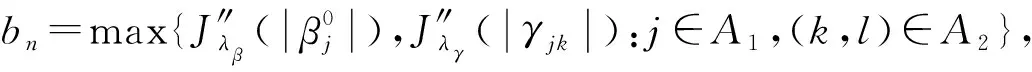
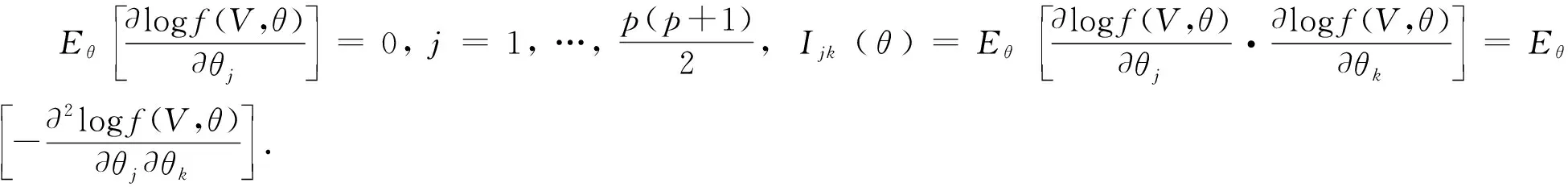
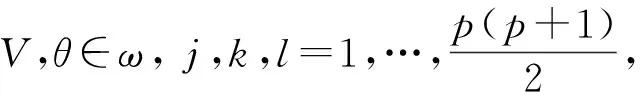
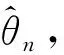
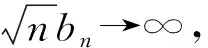
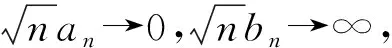
3 数值模拟

4 总结

