基于参数优化变分模态分解算法的列车振动信号分析研究

刘运思,左帆,彭亚雄,杜宪武,王晶

(1. 湖南科技大学岩土工程稳定控制与健康监测省重点实验室,湖南湘潭,411201;2. 中铁北京局集团(天津)工程有限公司,天津,300000)

随着城市地下空间的不断建设,新建地铁线路不可避免的反复下穿、密贴既有线。既有线运营列车振动与新建隧道施工相互影响,如何准确分析列车振动信号及其特征是保证施工环境稳定性的基础[1-2]。而在施工过程中,由于监测环境的复杂性、传播介质的反射和监测传感器的误差等因素,会使得测得的原始信号包含大量的噪声,掩藏了信号的真实特征。为了分析列车振动信号的真实特性,需要对原始信号进行降噪处理。

列车振动信号属于非平稳、非线性信号,目前对此类信号处理的算法有: 小波分析[3]、经验模态分解[4](EMD)、集合经验模态分解[5](EEMD)、变分模态分解[6](VMD)等。其中,杨春宇等[7]利用小波分析对原始监测数据进行去噪处理,再对去噪后的数据进行建模分析; 甘若等[8]基于小波分析中传统的阈值函数,结合其他学者提出的小波阈值函数,提出一种改进的小波阈值函数,并将其应用于变形监测数据的去噪处理; 易文华等[9]基于EMD 改进算法,对爆破振动信号进行了有效的去噪处理; 刘迎军等[10]为了解决EMD 的弊端,采用光滑样条拟合来代替原来的三次样条插值,可有效避免对噪声成分过度分解; 陈仁祥等[11]利用EEMD 变换可以有效地消除模态混叠,并提出一种IMF 自动化选取方法用于重构信号,降噪结果表明了该方法的可行性和有效性; 位秀雷等[12]提出一种基于EEMD 的去噪方法,克服了EEMD 去噪时IMF 难以有效处理的不足,使得降噪效果更优; 罗亦泳等[13]基于VMD 构建一种新的变形监测数据去噪方法,提高了变形监测数据的去噪精度和可靠性; 彭亚雄等[14]提出了基于VMD 算法的信号光滑降噪模型,能较好的去除高频噪声并对信号的低频能量影响较小。

小波分析中的小波变换需要人工选取小波基函数。当振动信号的不稳定性、非线性增强时,EMD分解时会出现较强的端点效应和模态混叠问题[15]。EEMD 算法在原数据中加入充分的零均值的白噪音,并利用EEMD 与IMF 成分相加的方式,消除了EEMD 的影响,消除了模态混叠。然而,EEMD 算法只能对最后效果和模态混叠进行局部消除,仍然面临着EMD 算法所带来的新问题,如添加的噪音残余、原始的噪音干扰等,对EEMD 技术在工程实践中的运用有一定的影响[16]。针对以上情况,Dragomiretskiy等[17]提出的VMD 作为一种新的分解信号方式,克服了模态混叠以及没有严格数学表达式的缺陷,但是模态个数K和惩罚因子α需要经验预设[18]。因此本文对VMD 算法中K和α进行参数优化,结合时频能量分析,得到包含有效信息的IMF,从而进行降噪处理,再通过重组还原真实信号特征,并应用到列车振动信号分析中。

1 VMD 算法

变分模态分解是一种自适应的算法,它通过反复搜索最优化的变分模态解,不断地修正每个模态解和中心频率,从而获得几个频段内的模态解。VMD 对样本和噪声更为稳健,具有更强的鲁棒性,即算法在其参数发生摄动时仍可使降噪指标保持不变。同时能够有效避免模态混叠现象。

VMD 算法中,将本征模态函数再定义为一个调幅-调频信号uk(t)=Ak(t)cos(φk(t)),其中: 相位φk(t)为非递减函数,包络线非负,Ak(t)≥0; 并且Ak(t)和瞬时频率ωk(t)=φk′(t)对于相位φk(t)来说是缓变的。

变分模态分解问题,即是拟研究一组模态uk,通过对输入信号f(t)进行最小二乘重建,并将各模态约束于一个可在线化估计状态下的中心频率ωk内,其表达式为

式中:{uk}={u1,u2,…,uK}为分解得到的K个模态分量;{ωk}={ω1,ω2,…,ωK}为各分量的频率中心;δ(t)为脉冲函数。

在此基础上,引入了二次惩罚函数(二次惩罚是一种经典的重建算法),并引入了拉格朗日乘数λ(一般在有噪音的情形下,如高斯型噪音,拉格朗日乘数是一种常见的用于限制条件的手段),从而将问题转化为非约束性变分问题。

由此,VMD算法通过迭代将信号分解成K个本征模态函数,交替寻优迭代后的uk,ωk,λ的表达式分别为的傅里叶变换分别为τ为噪声容忍度。

式中:ε为收敛容差,文中取1×10-7。

2 VMD 参数优化方法

2.1 VMD 参数优化

VMD 算法变分模型的目标函数是一个非凸优化问题,算法的收敛性与参数的设置有着很大的关系,VMD 中将输入信号自适应的分解成多个本征模态函数(IMF)。在此过程中,需预设分解尺度为K,K个IMF 分量的中心频率和带宽不断地迭代更新,使每个IMF 分量的估计带宽之和最小。而K的个数的大小需要根据信号的不同而设定,K值过小会导致欠分解,导致有效成分不能被完全分解出来; 过大则会出现过分解,分解出无用的虚假分量,从而影响最终解的评价。K值的选取需在避免模态混叠的情况下兼顾保留更多的信号特征,保证VMD 分解后IMF 分量中包含原始信号的全部特征信息,这也是算法的先验约束条件。而且在VMD 算法中惩罚因子α也会对分解结果产生影响。α又称为保真度均衡参数,其与原始信号的噪声水平有关。惩罚因子α的值越大,分解产生的IMF 分量的带宽越小; 惩罚因子α越小,每个IMF 的带宽就越大。

由于在密贴车站施工过程中,有来自施工时的工作噪声、监测传感器的误差、传播介质的变化等,使采集的列车振动信号比较复杂,对于不同的信号,K和α的值是不同的。因此,确定合适的参数是VMD 算法成功的关键。

2.2 降噪效果评价指标

首先要求模型降噪结果逼近原始振动信号(即算法逼近程度Mf越小越好,为与后续指标一同进行对比,采用算法逼近度越接近于1 越好),同时也要求降噪信号结果与原始振动信号充分相似(即算法相关度越接近于1 越好)。因此信号降噪成功的判定准则[19-20]为:其表示yi,yi′的协方差,表示标准差。

降噪算法f目标函数为其中:γ,1-γ分别为算法逼近度影响因子、相关度影响因子。本文γ取值0.3。

3 工程应用

3.1 实测信号降噪

本文研究的工程为北京地铁17 号线工程。17 号线十里河站作为三线换乘站,与既有10号线、14号线十里河站形成“T”字型换乘。以新建14 号线十里河站密贴交叉穿越既有10 号线十里河站为研究对象。密贴交叉部位为平顶直墙式双层车站,中间下穿段长21.6 m、宽度16.05 m、高度为8.32 m。现场采用L-20 型测振仪进行测试,测试点为密贴部位顶处,如图1 所示。选取密贴部位的一条典型振动信号进行分析,如图2 所示。该信号的采样频率为1 000 Hz,采样时间为4.5 s,共采集4 500 个采样点。

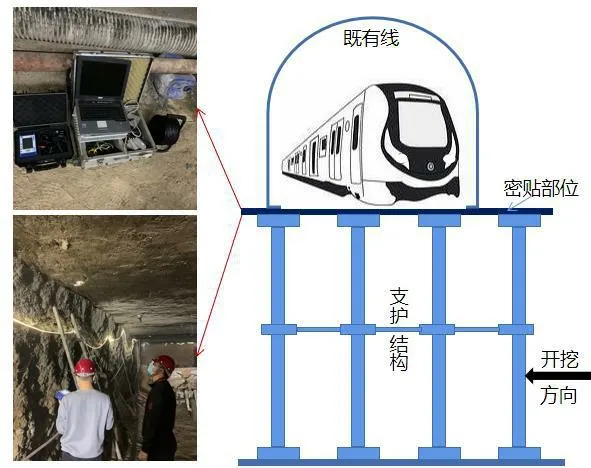
图1 监测点位置

图2 列车振动信号

使用VMD 算法进行信号分解时,对预设的参数进行以下处理: 双重上升的时间步长τ,取其默认值为0; 收敛准则的容忍度ε,通常取值1e-6; 针对惩罚因子α,通过反复试算(α分别取值5 500,5 000,4 500,4 000,3 500,3 000,2 500)并结合相关系数指标得到图3 所示曲线,由图3 可知: 在不同的K值下,随着α值的增大,相关性越差。当α=2 500 时,最优的|ρf|=0.986 1; 但当α小于2 500 时,信号分解的模态过多,出现模态混叠的现象,故本文α取值2 500。

图3 不同惩罚因子α对应的相关性指标

对于变分模态个数K,采用中心频率法,在α=2 500 的条件下,取不同K值对应的IMF 的中心频率,如表1 所示。当K=9 时,IMF1 的中心频率突变为3.01 Hz,此时出现了过分解的情况;K=5、6、7、8 时,各IMF 分量主频保持相对稳定。再通过相关性指标确定最终K的取值为K=8,如表2 所示。

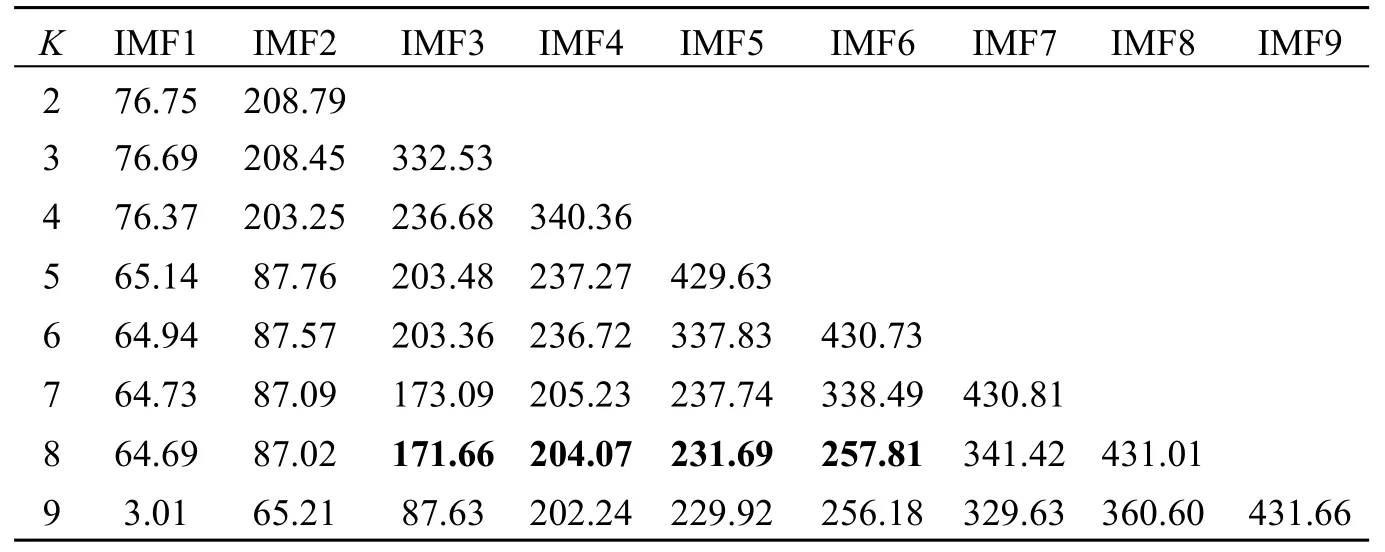
表1 不同K 值对应的IMF 中心频率

表2 K 的相关性系数指标

由此对原始信号进行VMD 分解得到的各个IMF 分量如图4 所示。共得到8 个IMF分量和一个噪声分量。IMF1～8 的中心频率依次增加。同时各个IMF 分量有着代表不同时间段的频谱,如图5所示,未存在模态混叠的现象,故对信号进行此参数下的VMD 算法合理。

图4 原始数据与本征模态函数

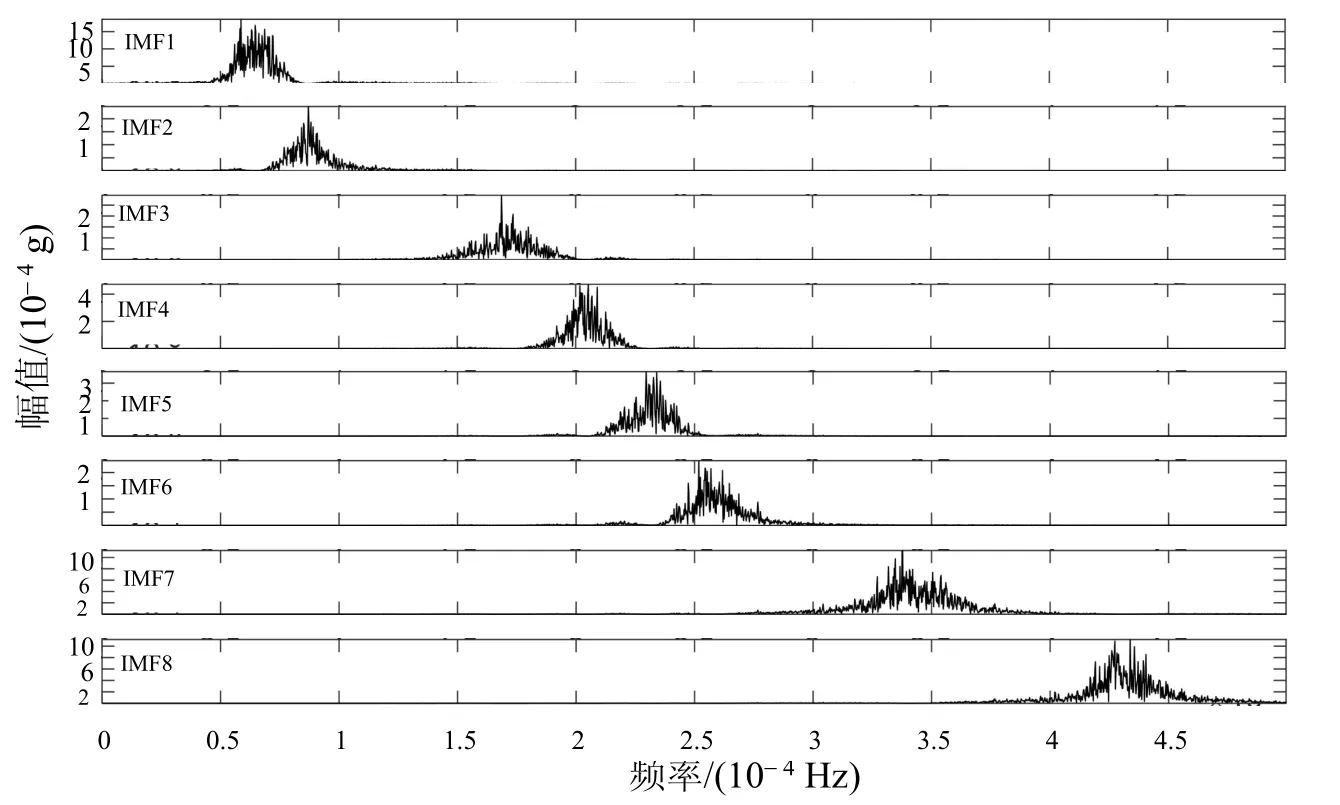
图5 模态函数FFT 频率-幅值谱分析图

3.2 时频能量分析

希尔伯特谱(Hilbert Spectrum)是希尔伯特-黄变换(HHT)得到的最直观结果,其反映的是信号时间、瞬时频率和幅值之间的关系。由此来分析信号中的分量随时间变化的规律,以识别局部特征。原理如下:

对于满足一定条件的实信号x,

则可构成解析信号

其中:a(t)=[x2(t)+xˆ2(t)]1/2,θ(t)=arctan(xˆ(t)/x(t))。

那么,其瞬时频率为

对振动信号进行HHT 可以识别出非平稳噪声在多个频带中沿时间轴的能量分布。由图6的Hilbert 谱可知,高频端和低频端都是噪声产生的,有用的信息比较集中在150～300 Hz 的频率内,即IMF3～IMF6。由图7 的频率为150～300 Hz 的Hilbert 谱可知,有效信息集中在0.5～3 s 内。因此,原始振动信号的时频能量主要集中在频率150～300 Hz 和时间0.5～3 s 内,见图7 虚线框。

图6 Hilbert 谱

图7 频率为150～300 Hz 的Hilbert 谱

3.3 不同IMF 组合降噪结果分析

针对各个IMF 分量,将其进行再组合后与原始信号对比分析,即将IMF1 叠加至IMF8 记为信号Fs18,IMF2 叠加至IMF8 记为信号Fs28,以此类推直至信号Fs78。评价指标为均方误差及相关系数和目标函数的最优值,如图8 所示。在信号Fs58 之前评价指标差距较小,因为在Hilbert 谱中可知,有效的频率集中在IMF3～IMF6 内,故超过此范围后,信号开始失真,不再具有原始信号的有效信息,如图9 所示。

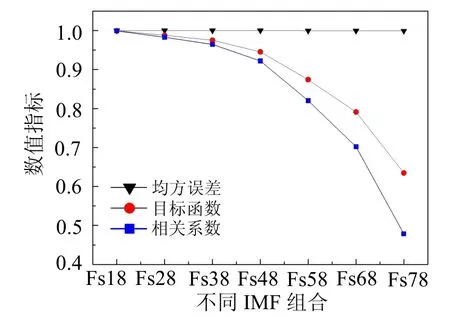
图8 均方误差、相关系数及目标函数的最优值

图9 不同IMF 组合与原始数据对比

4 降噪效果对比分析

为进一步分析得到VMD 这种自适应信号分析方法的优越性,对列车振动信号,与经验模态分解算法(EMD)、集合经验模态分解(EEMD)降噪方法进行对比。信号的模态分量结果如图10、11 所示,降噪目标函数指标如表3 所示。

表3 降噪目标函数评价指标

图10 EMD 对信号固有模态函数分量显示

图11 EEMD 对信号固有模态函数分量显示

由图10、11 及表3 可知,3 种算法均可对原始信号分解良好的固有模态函数,拥有一定的降噪效果。但是EMD、EEMD 随着模态函数的增加IMF 不再具有原始信号的特征,只具有变化的趋势。当信号重组时,可以很明显的发现VMD 的优势所在,在Fs28～Fs78 组合中,目标函数指标均远远大于其他两种算法。Fs18 组合中,因为EMD 和EEMD 的信号去噪程度低,使其与原始信号更加相近,所以指标优于VMD。此外,EEMD 通过对信号多次加入随机零均值和等方差白噪声来保证时域任意模态函数的连续性,同时减少模态混叠现象。与基本EMD 算法相比,EEMD 算法减少了模态混叠现象,也抑制了端点效应的发生。作为一种较新的自适应处理非线性和不稳定信号的算法,VMD 利用变分原理不断迭代更新各模态函数和中心频率,可以更有效地分解信号,避免了EMD 和EEMD 方法的缺点,且结果更好。

5 小结

由于地下空间施工环境较为复杂,使列车振动信号包含有大量的噪声,导致信号的真实特征被掩藏。针对此问题,提出了基于参数优化的VMD 算法进行降噪处理。

(1)对原始振动信号进行VMD 分解,得到8 个IMF,提取出了有效的特征信息。基于试算法确定α值,中心频率法确定K值,避免模态混叠现象,实现了最优降噪效果。

(2)利用Hilbert 谱,得到了有效信息集中在150～300 Hz 的频率内,从而可以有效去除高频噪声,同时对低频噪声的能量影响较小。

(3)通过均方误差和相关系数的评价指标,对不同IMF 进行组合,可得到与原始信号最大程度上相近的降噪信号,有效保存了信号的真实特征。

(4)对比VMD、EMD、EEMD 3 种降噪算法,虽都具有一定的降噪效果,但VMD 能更好的避免模态混叠现象,同时各种降噪指标均优于EMD、EEMD。验证了VMD 算法的有效性和优异性。