无锚框模型类梯度全局对抗样本生成

谢云旭，吴锡，彭静

（成都信息工程大学 计算机学院，成都 610225）

0 概述

各类深度神经网络模型的提出使得计算机视觉问题得以快速被解决，然而，这些模型容易受到对抗样本的严重干扰。对抗样本指针对图像人为设计微小扰动算法所生成的样本［1］，通过生成的扰动向量与原有干净图像进行叠加从而产生不同类型的对抗样本，能够导致各类深度神经网络模型以较高的概率产生错误的预测结果。对对抗样本进行分析有利于发现模型的缺陷及脆弱性，进而通过一定的防御手段来对模型进行有方向性的改进，因此，目前迫切需要对对抗攻击以及对抗样本进行研究。

现有的对抗攻击算法根据攻击目标的不同可以分成无目标攻击和目标攻击，2 种攻击模式截然相反。无目标攻击计算的是距离当前分类边界最短的方向及距离，其无明确的目标类指向性，而只与当前目标所属分类超平面的形状和高维空间位置相关。目标攻击计算的是当前目标距离目标分类边界的最小向量，其扰动方向和当前分类区域离目标分类区域的距离相关。

由于对抗攻击算法可以转化为一类非线性约束优化问题，其类型和最小化范数类型Lp相关，而不同的范数类型代表的对抗攻击算法理论截然不同。其中，无穷范数攻击［1-3］中最为典型的是快速梯度符号攻击方法（Fast Gradient Sign Method，FGSM）［1］，其攻击原理是利用损失函数的梯度来确定像素强度应改变的方向，以使损失函数向极值变化。通过网络结构将计算出的损失函数的梯度反传至输入样本上进而得到扰动。PGD（Project Gradient Decent）在FGSM 的基础上进行扰动的随机初始化，使得其产生的扰动能够概率性地跳出局部最优区间。在二范数攻击中，DeepFool 算法［4］通过有限次迭代计算扰动点相距当前分类决策边界的最短投影距离，即扰动多次计算离开当前决策区间的最短投影距离并进行叠加，直到分类器判断错误或者达到最大迭代次数为止。0、1 范数在形式上均存在稀疏性特点，SparseFool算法［5］在DeepFool的基础上控制生成扰动的稀疏性L0，其先通过L2DeepFool 算法计算扰动，再以L2计算的扰动作为目标，每次在一个像素点进行单像素扰动，最后达到控制L0的目的，其扰动像素点的选择基于每次梯度中对于其方向贡献最大的点。JSMA 算法［6］只改变少量的像素，每次会修改原有图像的个别像素并记录每个像素对于分类结果的影响的映射矩阵，通过迭代式的计算最终达到影响分类的目的。C&W 攻击［7］是一种基于优化的攻击，其核心思想是假设对抗样本是一个变量，要使其成功攻击分类器模型，必须满足与原始样本的距离要尽可能小，并且能够误导分类器模型对其进行错误分类。

本文针对计算机视觉任务中深度神经网络模型普遍存在的脆弱性及现有对抗攻击大多数基于后选框或单张图片的缺陷，提出一种类梯度全局扰动算法GCP。该算法首先利用单张输入图片中感兴趣的目标，以类为单位收集类梯度形成图片尺度扰动，然后结合数据集中多张图片及相应的图像尺度扰动形成针对整个数据集的全局扰动。在标准公开数据集的2 种视觉任务中进行实验，以验证GCP 算法相较现有对抗攻击算法的性能优势。

1 相关工作

目标检测和人体姿态估计是计算机视觉领域的2 个重要任务。

目标检测任务的目标是识别出输入图像中所有感兴趣目标的类别及位置。根据目标检测器定位目标方式的不同，现有目标检测模型可分为2类，即基于锚框和无锚框。基于锚框的目标检测器利用算法中的锚框在输入图像中提取大量的候选目标框，根据处理过程的不同又分为一阶算法和二阶算法：一阶算法包括SSD［8］、YOLO 系列［9-10］，这类算法的检测精度普遍低于二阶算法，但是拥有更快的速度；二阶算法包括R-CNN系列，如Faster R-CNN［11］，其特点是检测精度较高。最近的研究表明，改良的Transformer 模型SwinNet［12］可以借助其编码分层特征来高效完成目标检测任务。现有的对于目标检测的对抗攻击方法绝大多数都针对模型候选框或者单张图片进行扰动生成，如DAG（Dense Adversary Generation）［13］和UEA（Unified and Efficient Adversary）［14］。DAG为专门针对目标检测器Faster R-CNN 而设计的对抗算法，其根据Faster R-CNN 产生的候选框进行对抗扰动计算。由于Faster R-CNN 模型在推断时会形成大量的候选框，导致DAG 在生成对抗扰动时通常需要进行大量迭代，使得算法时间效率较低。UEA 是基于生成对抗网络（Generative Adversarial Network，GAN）的对抗攻击方法，其特点是需要额外时间来对GAN 模型进行训练从而可以有效模拟对抗扰动。UEA 与DAG 类似，也是一个基于攻击候选框的方法，由于锚框目标检测器的候选框数量巨大，导致对抗样本算法需要消耗大量的时间成本来对所有候选框进行扰动计算。

人体姿态估计是恢复输入图像中人类目标关节点的算法，其是计算机分析人类复杂行为模式和动作特点的关键步骤，在多种场景中得到广泛应用。文献［15］提出一种新型的行人检测姿势嵌入网络，通过嵌入行人的姿态信息解决现有行人检测方法中的遮挡问题。文献［16］提出一种多阶段网络，通过结构化的空间学习和捕捉瞬时信息，从而保证视频短时间结果的一致性。上述研究使用的深度神经网络模型在进行人体姿态估计时性能远超传统机器学习方法，在进行姿态估计求解时，其需将问题转化为对人体关键点的预测，即预测图像中人体关键点的二维坐标(x，y)。HPE 从具体求解策略上分为从上至下（top-down）及从下至上（bottom-up）的方法。自上而下的方法包括Hourglass 模型等［17-18］，其检测模式是从检测人体位置开始，首先在目标检测边界框中生成人的位置，然后对每个人类目标进行单独人体姿势估计。自下而上的方法［19-20］首先在输入图像中预测每个人类所有身体部位的空间位置，然后通过其他拟合算法对所有关节点进行分组。在性能方面，自上而下的方法通常计算成本较高但是具有更高的精度，而自下而上的方法通常具有更快的推断速度。现有对于人体姿态估计的对抗攻击方法缺乏相应研究，导致这类模型更易受到对抗攻击的影响［21］。文献［21］针对姿态估计的对抗攻击，研究基于最优化无穷范数的PGD 算法的FPE 及PPE，其方法是根据单张输入图像形成基于最小化无穷范数的扰动，其中扰动生成是根据整张输入图像中的所有对象来收集的，而不同类型的关节信息无法在收集梯度的环节中进行区别，因此，可能会造成攻击效果不佳的问题。

由于目前的对抗攻击算法是基于图像或模型候选框而生成的，均具有针对单张图片的限制，难以通过少量的样本对大量数据形成有效干扰，因此，相关对抗防御策略可以针对性地优化目标模型，使之能在一定程度上有效抵抗其干扰。在近期的研究中，文献［22］以数据集内多张图片为基础生成一个针对分类问题的全局对抗样本算法UAP（Universal Adversarial Perturbations）［22］，其算法生成的全局对抗样本具有较高的泛化能力，并可以有效地对整个数据集形成干扰。文献［23］在UAP 的基础上将此类全局对抗样本应用到语义分割问题中。由于该类全局对抗算法体现出了高泛化性，因此其对整个数据集或大量数据形成了有效干扰，该类对抗样本对于各类深度学习模型的危害尤为严重。同时，此种全局扰动在很多计算机视觉任务中尚未得到足够重视，因此，对抗防御难以利用相关的对抗样本进行有效研究。相较图片分类等较为简单的计算机视觉问题，目标检测、人体姿态估计除了需对输入图像中可能存在的多个大小不同的目标进行分类，还需要针对每个目标找到其空间位置。直接延用UAP 的全局对抗理论难以形成精准的对抗攻击，即在扰动不可见的同时干扰模型的预测结果。

本文提出一种类梯度全局扰动算法GCP，该算法首先利用单张输入图片中感兴趣的目标类作为单位快速进行类梯度收集并生成图片尺度扰动，以类为单位进行梯度收集可以着重针对输入图像中目标类别间的联系与区别，通过一次性收集同一类别内所有目标的梯度，达到快速收集梯度同时凸显不同类别区别的目的。基于现有经典对抗算法形成图像尺度的对抗扰动，在此基础上，结合数据集中多张图片及相应图像尺度扰动形成针对整个数据集的全局扰动。在标准公开数据集Pascal VOC［24］和MSCOCO-keypoints［25］上的2种计算机视觉任务中进行实验，通过多种计算机视觉任务中全局对抗样本的有效性来说明深度神经网络模型在高维决策边界之间存在一定的几何相关性，利用这类对抗扰动有利于对模型进行改进。

2 网络设计

相较锚框模型［11］，无锚框目标检测器［26-28］的结构更精简统一［29］。本文采用CenterNet 模型［26］作为目标网络，CenterNet 模型是典型的无锚框模型，在结构上使用全卷积结构。在CenterNet 模型中，输入图像满足img ∈ℝW×H×3，模型结果为图像中目标中心点热图H，其中R是模型的下采样比例，c是中心点的类别数量。在目标检测预测过程中，一个预测值vi，j，c=1 对应于一个被检测到第c类的目标前景中心点，而vi，j，c=0 对应一个被检测到背景的点。该网络采用可变形卷积网络（Deformable Convolutional Network，DCN）［30］，同时可结合多种典型带全卷积结构模型用于预测空间热图H，如沙漏模型Stacked-Hourglass［31］以及DLA（Deep Layer Aggregation）模型［18］。CenterNet以中心点检测为基础，通过中心点及回归目标的高、宽来定位一个完整目标的大小和位置。

除了目标检测外，CenterNet 还可以执行人体姿势估计任务，其目标是对输入图像中每个人类目标的所有关节空间位置进行预测。人体在模型中的姿态表现是一个拥有k×2 维的属性，其中，k为人体目标的关节数量，2 代表每个关节为包含坐标的空间位置。姿态预测共分为2 个步骤，在首步进行预测时，模型会直接预测人类目标的中心点Kpi，再通过估计一个回归偏移量J*来达到对所有k个关节点的首步预测，其中，偏移量，从而可以 得到单阶段预测结果为同时，模型会仿照目标检测任务的预测模式对输入图像中人类关节进行k关节点的多目标预测，与第一阶段不同的是，每个关节点都为不同类别的中心点，共计k个类别。最后，网络会结合两步预测结果，将首步回归到的关节点Li与第二次预测中第i类的目标进行校正，其最终结果只会考虑人体目标检测边界框内的候选结果，从而提升模型预测的鲁棒性。

3 对抗攻击算法

3.1 全局扰动

产生对抗扰动的问题可以归纳为以下通用约束性优化问题，如式（1）～式（3）所示：

其中：p是最小化的范数类型，{p|p∈0，1，…，∞}；函数表示无锚框模型检测到的物体类别；x和xadv分别表示干净图像和对抗样本。优化问题的目标是在施加扰动向量r后，模型对对抗样本xadv的推断结果与干净图像x不同。

由于产生的是全局扰动，参与生成扰动的多个数据为x={x1，x2，…，xm}并满足{x|x⊆U}，其中，U为一个已知数据集，因此全局扰动可以转化为以下约束性优化问题，如式（4）～式（5）所示：

其中：P为满足一定约束条件的概率值；1-κ为全局扰动干扰下模型的推断正确率。

本文算法采用收集类梯度的方式来产生扰动，原因是同一类的目标在梯度上存在近似特点。同时，由于CenterNet 的检测结果f(x，obj)依赖于检测到的中心点keypoint 及偏移量offset，考虑到偏移量和CenterNet 目标中心点keypoint 同时对结果产生影响，因此，利用对抗扰动攻击上述两者以欺骗模型。此时可以将上述约束性优化问题转化为式（6）～式（8）：

其中：obj 为输入图像中属于i类的目标，其中包含检测到的相应的中心点和偏移量；f(x，obj)为CenterNet的检测结果；C为检测器CenterNet 检测到的目标类别。全局对抗扰动的生成流程如图1 所示。

图1 GCP 算法总体流程Fig.1 Overall procedure of GCP algorithm

3.2 扰动生成

第一步针对单张图像生成图像尺度的对抗扰动，具体方法为采用最小化L∞范数的PGD 来生成L∞扰动。由于算法按照类别进行梯度收集，同类别目标梯度具有相似性，在姿态估计任务中输入图像的目标在模型中体现为人类关节的中心点，因此首先需要得到所有检测到的中心点并按照类别进行分类，即P={P1，P2，…，Pk}，计算同一类别总损失并反传至输入图像以计算类梯度rc：

其中：LLosscategory为收集到的属于c类的类损失；pi为属于PC的类中心点；rc为通过模型反向传播得到的图像扰动。

将梯度进行规范化并叠加收集到的类梯度，得到单张图片的扰动，如下：

其中：ε表示单步步长，有，T表示对抗算法中迭代步的最大次数，η表示扰动的总步长。

如图2 所示，通过数据集中的多张图片形成对整个数据集的全局扰动。首先收集数据集中参与全局扰动的k个数据的图片尺度扰动，为了确保收集到的扰动满足rG的范在规定的扰动步长ζ之内，需要进一步将全局扰动投影到半径为扰动半径ζ的球o上，最终得到全局扰动，如下：

图2 单张图像扰动与全局扰动示意图Fig.2 Schematic diagram of single image perturbation and global perturbation

其中：k表示参与全局对抗样本生成的数据总数。

4 实验设置

4.1 数据集

Pascal VOC 是一个用于多种计算机视觉任务的常用数据集，该数据集包含人类等20 类常用目标，包括Pascal VOC 2007—2012 的训练集、验证集及测试集。本次实验涉及的攻击使用其测试集数据，数据总量为4 952 张图像。MS-COCO 数据集一共包含80 个目标类别，本次实验采用的是COCO-val 2017中带人类姿态估计的数据标签 MS-COCO-keypoints，数据量总共为5 000 张图像，共包含11 004 个人类目标，平均一张图像中有2.2 个人类目标。

4.2 实验环境

本次实验基于64 bit 的Windows10 操作系统，在一台戴尔（Dell）Precision T5810 图形工作站上开展实验，CPU 型号为I9-7960X-@2.8 GHz 处理器，GPU为 NVIDIA GeForce GTX1080Ti 8 GB 显卡，采用PyTorch 深度学习框架，运行环境为PyTorch 1.1.0，使用的主要软件工具为 Pycharm。

4.3 评价指标

使用4 个指标来评估所生成的全局对抗样本的对抗性能，包括平均精度均值（mean Average Precision，mAP）、攻击成功率（Attack Success Rate，ASR）及可见性指标PL0和PL2。

mAP 为数据集中人类关节点的平均精度均值，其值为查准-查全（Precision-Recall）曲线的下侧面积，其中Recall、Precision 分别为查全率和查准率，RRecall=TTP/(TTP+FFN)，PPrecision=TTP/(TTP+FFP)，其 中：TP 表示真实是正样本且预测为正样本的数量；TN表示真实是负样本且预测为负样本的数量；FP 表示真实是负样本但预测为正样本的数量；FN 表示真实是正样本但预测为负样本的数量。

ASR 主要计算模型受全局对抗样本攻击前后mAP 值的变化情况，其代表模型抵抗全局对抗攻击的能力，计算如式（15）所示：

其中：mmAP，clean和mmAP，attack分别代表攻击前后模型预测的mAP值。攻击成功率越低，代表该模型对抗白盒攻击的性能越高。

使用对抗样本可见性指标用于衡量全局对抗扰动的可见性强弱，扰动可见性越高，越容易被人类发现，而扰动可见性越低，越能与干净样本融为一体。具体可见性指标由PL0和PL2决定，其中，PL0控制扰动稀疏性，PL2控制扰动像素强度，计算分别如下：

其中：pxi为对抗样本中的像素值；n为图像像素的总数量；k*为扰动改变的像素数量。

5 结果分析

5.1 目标检测任务

在Pascal VOC 挑战赛的测试数据集上进行实验，测试集共包含4 952 张图片用于测试全局对抗攻击算法GCP 在目标检测任务中的有效性，实验结果如表1、表2 及图3 所示。

表1 Pascal VOC 数据集上的量化指标结果Table 1 Quantitative indicator results on the Pascal VOC dataset

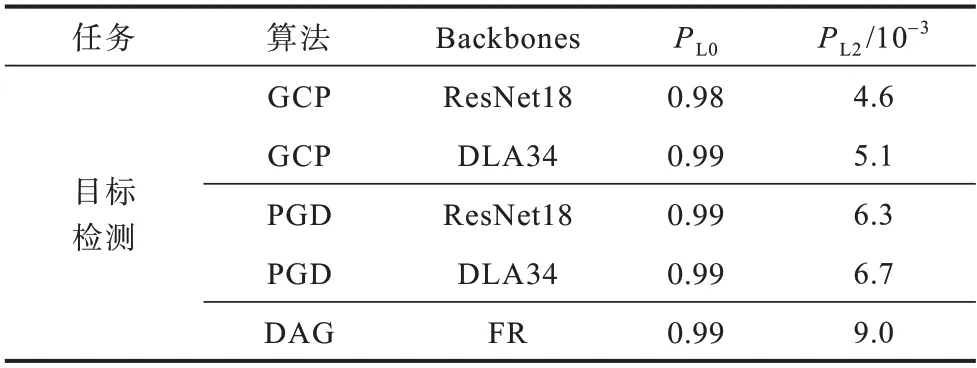
表2 对抗扰动可见性量化指标结果1Table 2 Quantitative indicator results 1 of counter disturbance visibility

图3 Pascal VOC 数据集上干净样本和对抗样本的可视化结果Fig.3 Visualization results of clean and adversarial samples on Pascal VOC dataset

表1 数据为Pascal VOC 数据集上目标检测任务对抗攻击结果，其中，Backbones 代表骨干网络，mmAP，clean和mmAP，attack分别为攻击前后的mAP值，ASR 为对抗攻击成功率，Time 代表对抗扰动单张推算时间。从表1 可以看出：GCP 算法在骨干网络为DLA34 时达到最高的对抗攻击成功率，与单张图片算法PGD 的ASR 保持一致，达到0.93，但其推段时间仅为PGD 算法的1/13；在骨干网络为ResNet18 和ResNet101时，GCP 算法的ASR 值较骨干网络为DLA34 时低，分别为0.89和0.91，其原因是骨干网络结果较为简单，与此同时推段时间也更短，达到0.05 s 和0.08 s；DAG 为攻击Faster R-CNN的对抗攻击算法，虽然ASR较高（达到0.92），但是由于DAG 为针对候选框的对抗攻击算法，其推断时间远高于基于全局和基于单张图片的方法。

表2 所示为全局扰动算法GCP 在目标检测任务中与现有算法的可见性比较，较高的可见性意味着生成的对抗样本更容易被人类发觉。本次实验涉及的对抗方法都为非稀疏扰动算法，因此得到的PL0值都接近1.0。在PL2的比较中，基于骨干网络ResNet18 的GCP 全局对抗样本扰动值最低，为4.6×10-3，DAG 对抗算法的PL2达到最高，为9.0×10-3，表明本文算法生成的对抗扰动强度较低，不可见性更高。

图3 所示为样本的可视化结果，第1 行是输入图像，第2 行是干净样本检测结果，骨干网络为DLA34，第3 行是GCP 的对抗攻击结果及扰动，参与生成全局扰动的图片尺度扰动为1 000。

5.2 人体姿态估计任务

本次实验在MS-COCO-keypoints 挑战赛的测试数据集上进行，测试集共包含5 000 张图片，用于测试全局对抗攻击算法GCP 在人体姿态估计任务中的性能，实验结果如表3、表4 及图4～图6 所示。

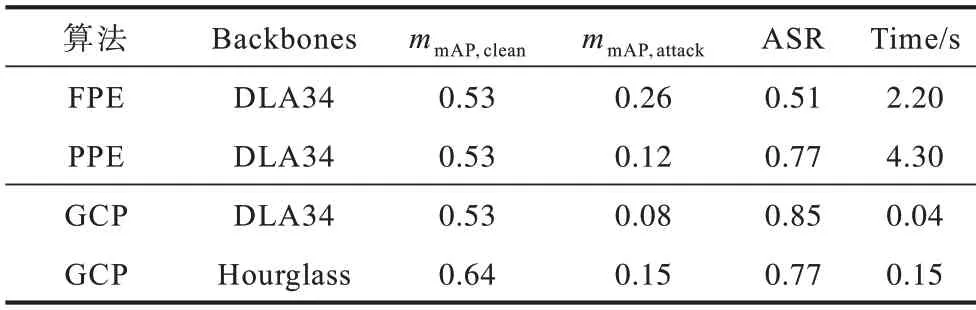
表3 MS-COCO-keypoints 数据集上的白盒攻击量化指标结果Table 3 Quantitative indicator results of white box attacks on the MS-COCO-keypoints dataset

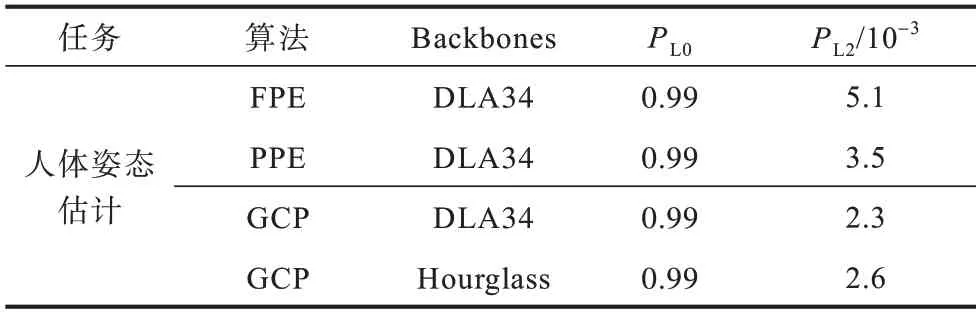
表4 对抗扰动可见性量化指标结果2Table 4 Quantitative indicator results 2 of counter disturbance visibility

表3 数据为 MS-COCO-keypoints 数据集上人体姿态估计对抗攻击结果。从表3 可以看出：相较现有算法，GCP 算法的性能更好，mmAP，attack更低，在骨干网络为DLA34时，基于GCP 的对抗扰动在数据集中mmAP，attack为0.08，其相应的ASR 为0.85，是对抗算法FPE 的166%，为PPE 算法的110%；骨干网络为Hourglass 时GCP结果略低于DLA34，其原因是Hourglass 模型复杂度更高，受对抗攻击干扰的抵抗能力较高；在生成及推断速度上，全局扰动GCP 达到25 FPS，基本满足实时攻击的要求。因为现有算法多数基于攻击图片和候选框，需根据攻击目标单独计算梯度及扰动，而全局扰动不受图片数量或模型生成的候选框的限制，其生成及推断时间远优于现有算法。

表4 总结了在姿态估计任务中全局扰动算法GCP 与现有算法的可见性比较。由于本次实验所涉及的方法均为非稀疏扰动算法，因此得到的PL0值都接近1.0。在PL2的比较中，本文算法的扰动值均低于3.0×10-3，比现有算法的可见性更低，这表明本文算法生成的对抗扰动相对现有算法更不容易被人类所发现。

图4 所示为在不同数量图像生成的全局扰动影响下的mmAP，attack结果。从图4 可以看出：对抗攻击的整体效果随着参加生成全局扰动图像的增加而加强，同时在组别为10 的情况下显示出全局扰动效果不佳，mmAP，attack仅从干净样本的0.53变为0.48，其 原因是过少的样本参与的全局扰动无法对整个数据集形成有效的攻击，过少的样本无法提取出针对人类目标的所有类型关节点（k=17）的信息及梯度，如在10 组别下，提取出的一类关节点仅为0.6张，同时攻击效果会受到输入图片中人类数量、大小等其他因素的影响；mmAP，attack在数据量为1 000 的全局扰动下可以达到最好效果，而在数据量为2 000 时效果变差，其原因是生成全局扰动的数据过多，对抗扰动会对产生扰动的数据形成过拟合。

进一步测试生成全局扰动的循环次数对模型的影响，结果如图5 所示。从图5 可以看出：在扰动数为1时，扰动显示出相对较弱的性能；在扰动数为5 时性能达到最高，攻击成功率ASR 在图像数为1 000 时达到0.91；当扰动数为10时，性能相对5 时较弱，但同样在图像数为1 000 时达到最高性能，其值为0.89。过高或过低的循环数形成的全局扰动会基于数据集形成欠拟合和过拟合，前者较低的循环数无法有效形成全局对抗样本，从而难以影响数据集中的所有数据，后者形成的扰动对参与的图像形成依赖，无法较好地影响数据集中的其他图像。

图5 全局扰动循环数对ASR 的影响Fig.5 Influence of global disturbance cyclic number on ASR

图6 所示为实验数据集中受全局扰动影响的图像的可视化结果，第1 列为干净人体姿态估计检测结果，第2、第3、第4 列分别为生成数据量为100、1 000 和2 000 的全局扰动影响结果，第1 行图像为较简单目标图像，第2 行为普通多目标图像，第3 行为较复杂多目标图像，第4 行为不同数量图像参与的全局扰动。由图6 可以看出，在图像数为1 000 时形成的扰动性能最高，在相应的可视化图像中可以看到此时模型检测出的结果最少，其发生错误的概率也最高，体现出全局对抗样本在数据集中的有效性。

图6 全局扰动可视化结果Fig.6 Global disturbance visualization results

6 结束语

本文提出一种全局扰动对抗攻击算法GCP。首先利用输入图像中的目标类，以类为单位收集类梯度，按照此方式进行梯度收集可以利用类内目标梯度上的相似性，避免直接叠加扰动对扰动性能的影响，进而生成图片尺度扰动。在此基础上，基于一定数量的图片尺度扰动形成针对人体姿态估计任务的全局扰动，全局扰动克服了现有对抗扰动生成方法基于图片或基于候选框的缺点，可以针对大量数据形成有效的干扰，同时在推断速度上基本达到实时攻击的要求。实验结果验证了GCP 算法的有效性。然而，由于全局对抗样本的生成需要多张图片尺度扰动及若干循环迭代过程，其生成过程具有较高的时间复杂度并需要更多的超参数。下一步将改善全局对抗样本，优化参数设置，使算法能适用于更多的网络并且性能更高。在此基础上，进一步探究深度神经网络模型中的潜在安全漏洞问题，结合全卷积结构可解释性方法及掩码技术，提高对抗样本的不可见性，为深度神经网络模型抵抗对抗样本的相关研究提供参考。