高寒地区拱坝运行期保温板脱落位移和应力场分析

马基栋,武志刚,费新峰,吕维娟,李高超

(1.国家电投集团青海黄河电力技术有限责任公司,西宁 810016; 2.西安理工大学 水利水电学院,西安 710048)

0 引 言

混凝土拱坝是一种大体积混凝土建筑,因其具有整体稳定、超载能力强的特点,常被选为巨型水库的主要水利基础设施[1]。近年来,国内修建了许多高薄混凝土拱坝,如锦屏一级(高305 m,厚高比0.207)、小湾(高294.5 m,厚高比0.238)、白鹤滩(高289 m,厚高比0.190)、溪洛渡(高285.5 m,厚高比0.210)和二滩(240 m,厚高比0.232)等。拱坝具有明显的荷载特点:应力状态和开裂控制受周围温度条件、水库水位及其材料特性影响显著,尤其是对外界气温和水温的比较敏感,温度变形受外界约束比较大,因此在拱坝内可能出现较大的温度应力[2-3]。尤其在高寒地区,夏季炎热,冬季寒冷且气温年内变幅大,温度荷载对拱坝应力和内力的影响可能会超过其上的水荷载。一旦混凝土表面的保温板损坏失效后,混凝土会直接与空气接触,表面温度发生变化,产生温度应力,在低温环境下,当产生的拉应力超过混凝土的允许拉应力,就会引起表面裂缝的产生。因此,温度是拱坝结构健康运行的主要负荷。

大坝混凝土的保温可有效防止温度裂缝的发生[4-6]。基于此类问题,不少学者开展了相关研究。崔金良等[7]对拉西瓦拱坝表面挤塑聚苯乙烯保温板效果进行试验研究,得出当外界温度在-1.9～9.95 ℃时,保温层下混凝土表面温度为2.73～6.1 ℃,保温效果良好。此外,张晓飞等[8]、Chen等[9]通过数值模拟方法对保温板效果和不同保温层厚度对混凝土温度场和温度应力的影响,表明表面保温可以有效保温且减小坝体最大温度拉应力。在寒冷地区,保温板被认为是在各种工程结构中减少热传递的最安全和最有效的方法[10-11],它为建筑提供了免受外界环境温度影响的保护,消除了结构与温度直接接触的热桥。因此,严寒地区混凝土拱坝的长期保温研究对于有效控制结构的温度场,防止结构损伤、冻融循环、裂缝等耐久性问题具有重要意义[12]。

除了试验和数值模拟方面,许多学者在混凝土大坝温度及其荷载效应的结构健康监测研究方面进行研究。Yang等[13]、Tatin等[14]、对建立考虑原型监测数据的统计模型进行深入研究,前者则对原型监测数据存在的奇异值进行评判,确保统计模型的精确性,后者考虑了大坝温度的水温的垂直梯度和大坝形状对模型的影响。Gu等[15]、Wei等[16]、Bian等[17]使用智能优化算法以增强建模的准确性,包括随机森林算法、粒子群优化算法、经验模态分解等。李秀琳等[18]、林锋等[19]以实测资料为目标进行温度场、位移和应力场的反馈分析有助于仿真计算采用反演的材料参数,从而提高仿真的精度。因此,结合原型观测数据深入分析不同运行条件下坝体结构可能产生的异常,也是评价高寒地区混凝土坝保温板脱落问题的又一重要手段。

本文以混凝土-挤塑聚苯乙烯复合材料结构为研究对象,结合现场实测温度和位移资料,采用有限元软件对实际保温板脱落前后情况的温度、位移和应力进行三维有限元建模分析。并结合统计模型分析保温板脱落后的异常变化,综合对高寒地区的拱坝的安全进行评价。

1 混凝土表面保温计算原理及边界条件

1.1 保温板-混凝土复合保温结构模拟方法

在混凝土大坝表面铺设保温层后,表面保温层与大坝混凝土的结合为层状复合结构。此时,大坝上的温度荷载不再是大坝与外界环境的温度直接交换,而是需要通过外层保温板和内部混凝土进行传递。由于保温板和大坝混凝土的传热系数不同,且两种材料的性能和厚度不同,边界形式发生了较大的改变。因此,采用数值模拟方法时,保温板相当于混凝土表面的保护层,建立混凝土和保温层构成的复合结构的热传导模拟方法,以减缓混凝土与外界的热交换,提高表层混凝土的温度。

同种保温材料不同厚度的混凝土表面放热系数之间的关系公式为:

(1)

(2)

式中:T为混凝土表面温度;n′为表面外法线方向;βs为关于导温系数λs、厚度h、放热系数β的函数;λ为混凝土导温系数;n为保温层材料种类数;hi为第i层保温材料厚度;λsi为第i层保温材料的导温系数;Ta为外界温度。

混凝土、保温层与环境之间的热交换及等效过程如图1所示。

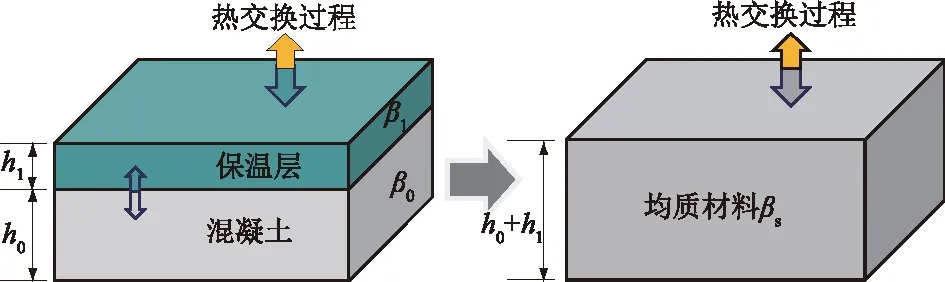
图1 混凝土-保温层复合材料等效示意图Fig.1 Equivalent schematic diagram of composite material composed of concrete and surface insulation layer

1.2 温度边界及热传导

根据大坝实际环境,采用热平衡分析方法计算大坝的稳定温度场。其中计算的初始条件和边界条件:混凝土与水接触的边界为第一类边界条件;混凝土与空气接触的边界为第三类边界条件,布设保温板时亦采用此边界条件;混凝土受到的太阳辐射强度设置热流边界,日照的影响相当于周围空气的温度增高了ΔTn=R/β[20]。边界条件原理如下:

第一类边界条件为

T(τ)=f(τ) 。

(3)

第三类边界条件为

(4)

考虑日照后的边界条件为

(5)

连续热传导方程为

(6)

式中:f(τ)为混凝土接触的水温关于时间的函数;τ为时间;q为混凝土表面的热流量;R为混凝土吸收部分热量;a为热传导方程中的系数;θ为混凝土绝热温升。

2 模型建立

2.1 某高寒地区拱坝概况

我国西北高寒地区修建的某高薄拱坝,最大坝高250 m,拱冠梁底部最大厚度49 m,拱坝厚高比0.196。工程坝址处年平均气温7.3 ℃,1月份平均最低气温-13.7 ℃,7月份平均最高气温25.6 ℃,气温年变幅较大。拱坝工程的永久暴露面采用挤塑聚苯乙烯保温板(Extruded Polystyrene Board,XPS)作为永久保温材料,其具有完美的闭孔蜂窝状结构,特殊的分子结构使之具有极佳的保温性能,但也存在阻燃性能低的缺点[21]。拱坝采用7组垂线对坝体水平位移监测,其中7号、11号、16号坝段对应3#、4#和5#重点监测断面,垂线观测时间从2011年至今。2013年9月29日,因某些原因,主坝坝后保温板脱落,主要脱落区域位于下游面高程2 405 m坝后桥与高程2 460 m坝顶之间,由左岸拱端延伸至靠近右岸电梯井区域,左岸拱端处由坝顶至岸坡底部亦有脱落区域。2014年完成保温板修复,保温板脱落区域附近的混凝土近一年长期暴露在空气中,受外界气温直接影响,如图2所示。

图2 拱坝保温板脱落情况Fig.2 Photo of detachment of thermal insulation board on arch dam

2.2 有限元模型及参数选取

有限元计算模型包含坝体和山体两部分。坝体共分为22个坝段,包含表孔、中孔、底部及廊道等细部结构,并考虑垂线监测点位置。山体部分按照实际地形等高线进行适当简化,建模范围采用反演得到的模型几何尺寸即上下游及底部边界均为1.637倍坝高[22]。模型有限元网格划分包含97 329个六面体单元、8 103个退化六面体和374个四面体单元。模型整体单位数目为105 806,总节点数目为113 746。建模方向为x向为顺河向,向下游为正;y向为竖直方向,向上为正;z向为横河方向,由左岸指向右岸为正。有限元模型范围及划分如图3所示。

图3 模型范围及有限元网格示意图Fig.3 Domain and grids of finite element model

有限元数值计算参数主要包括结构力学参数以及相关热力学参数,如表1所示。

表1 有限元计算参数Table 1 Parameters of finite element calculation

2.3 模拟方案边界条件对比

拱坝保温板脱落时已运行多年,坝体表面温度主要受上下游水温和气温影响,内部温度则已逐渐趋于稳定。首先计算稳定温度场,其次采用瞬态方法设置下游面逐日气温边界,计算2013—2014年坝体在下游面保温板-空气对流边界下的位移与应力。保温板完好时与实际保温板脱落的边界条件模拟如图4所示。两种模拟主要差异在于下游面保温板完好区域设置为保温板-空气对流边界,参数为保温板等效表面散热系数。保温板脱落区域设置为混凝土-空气对流边界,参数为混凝土的表面散热系数。

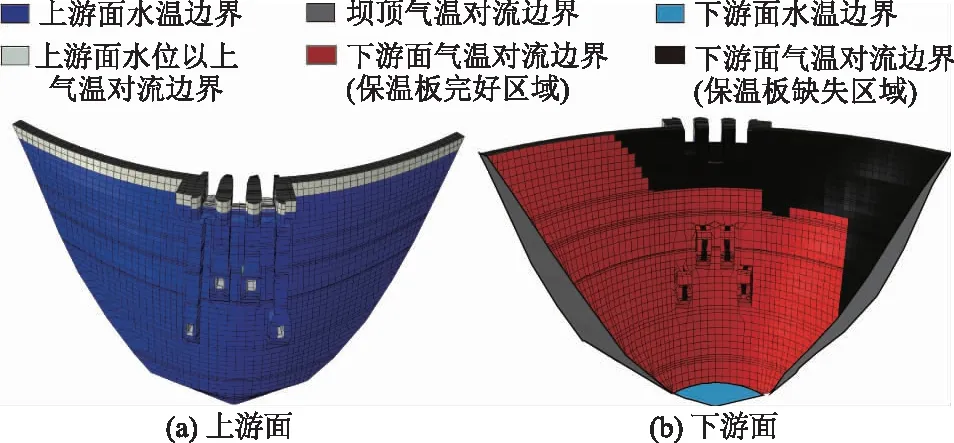
图4 温度场计算边界Fig.4 Boundary of temperature field computation

3 保温板脱落分析

3.1 初始温度场

初始温度场的模拟结果如图5所示,坝体稳态条件下温度基本在3.0～10.5 ℃,坝体温度上游面与库水温度分布一致,下游面与外界气温接近。重点监测断面的坝体内部温度基本维持在5～7 ℃。在水面以下,随着高程增加,坝体厚度减小,受上游水温和气温的影响也越大,坝体温度逐渐增加。而坝顶主要受外界气温的影响,因此温度接近气温值。

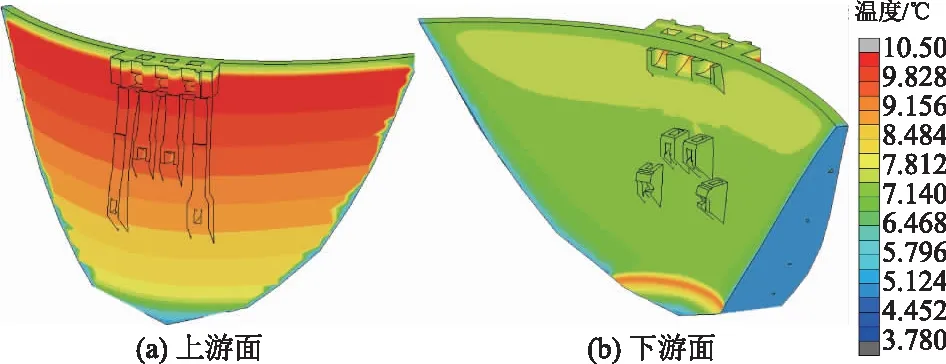
图5 保温板初始温度场云图Fig.5 Contours of initial temperature field of thermal insulation board

3.2 温度变化分析

结合图3特征点分布情况,由图6所示的各特征点温度变化可知:保温板脱落后坝顶及坝体近下游表面混凝土温度出现明显变化,而坝体内部混凝土温度变化较小,基本维持稳定。在同一断面,脱落区域内特征点的温度在脱落(2013年9月29日)前后的变化最大幅值为17 ℃左右,且与气温保持一致的周期性。可见保温板脱落致使坝体表面混凝土与空气的直接接触是导致温度变化的主要因素。而各特征断面完好区域的混凝土温度仍具有表面混凝土对气温较为敏感的特点,变化幅值为2 ℃。并且对于同一断面同一区域内的特征点而言,越靠近坝体表面,其温度变化越显著,而4#、5#这2个特征断面特征点的温度变化整体上温度变化趋势基本一致。进一步表明保温板脱落对于坝体混凝土的影响基本上存在于混凝土表面,并未对内部混凝土温度产生较大影响。

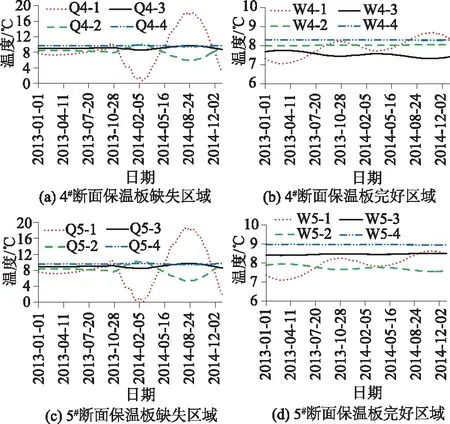
图6 特征断面时期坝体温度曲线Fig.6 Temperature curves at characteristic points

选取与特征点对应的典型温度测点,绘制数值计算与温度计监测值对比曲线如图7所示,其中T5-1测点位置对应Q5-1,T4-1测点位置对应Q4-4。由图7可见,数值计算温度值与实测温度值整体变化规律呈现一致性,坝内温度变化较为平稳。坝体表面温度则较大,且具有明显周期性。此外,Q5-1和Q4-1数值计算和实测数据的平均差值分别为0.34 ℃和0.336 ℃,表明温度数值计算结果相对合理。

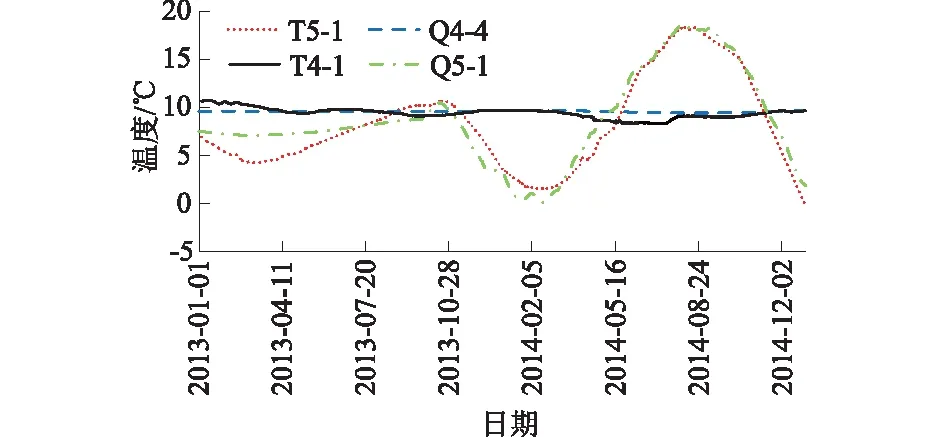
图7 数值计算与监测温度值对比曲线Fig.7 Comparison of temperature between numerical calculation and monitoring

3.3 位移分析

3.3.1 数值模拟结果

图8为2013年9月—2014年6月特征时期坝体仅在温度荷载下的顺河向位移云图。2013年9月保温板未脱落前,温度荷载下的位移变化符合拱坝基本特征:最大位移位于拱冠梁坝顶处,呈现拱冠向岸坡坝基处逐渐减小的分布特征。保温板脱落后,由于表面混凝土与空气的直接接触,其表面温度与气温的温差增大,整体呈现出脱落区域大于完好区域的分布特征。此外,值得关注的是:2013年12月,右坝段脱落区域向下游位移明显增加,结合保温板脱落后的温度变化特征来看,保温板脱落后,冬季低温时期整个脱落区域失去保温板的保温隔热作用,直接暴露于冷空气中,坝体表面温度较常年更低,温降荷载更显著,坝体向下游方向发生了较大的位移,数值为0.8 mm。

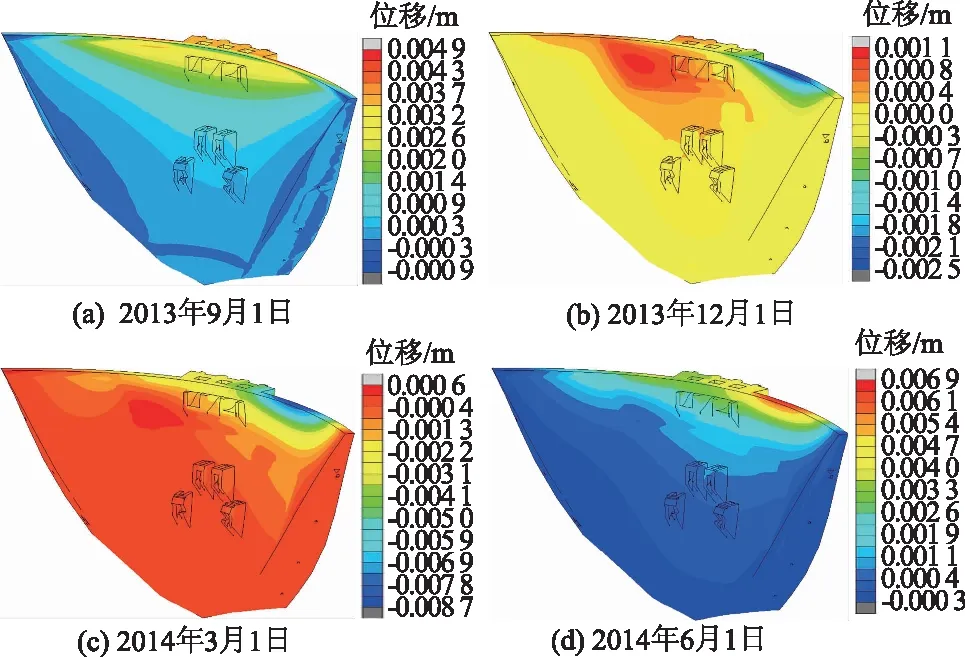
图8 不同特征时期坝体顺河向位移云图Fig.8 Contours of dam body displacement along the river in different characteristic periods

图9为各特征断面下特征点的位移变化。各断面不同高程坝体下游面的3个特征点位移变化差异明显,坝顶特征点Q4位移最大,其次为Q4-1,这两个特征点均位于保温板脱落区域,均呈现一定周期性,而保温板完好区域的特征点W4-1位移明显较小,且并未呈现周期性,这主要与温度变化特征下的温度荷载相关。显然,保温板脱落区域特征点对外界气温变化更敏感,相应的温度荷载更大。而对于同一高程特征点而言,距坝体下游面越远的测点,温度位移值越小。对比两个特征断面,4#断面和5#断面在保温板脱落后位移变化在不同区域分别表现出一致的变化规律,保温板脱落后的2014年位移较未脱落时产生了明显增加,增加的位移分别为2、1.5 mm左右。

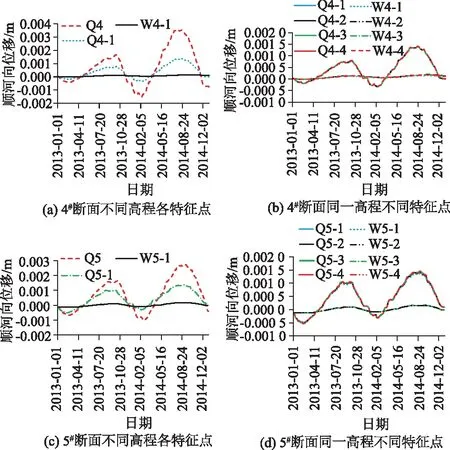
图9 各段面特征点在温度荷载下的位移变化曲线Fig.9 Displacement curves of characteristic points of each section under temperature load

3.3.2 实测资料分析

为定量分析保温板脱落对坝体关键部位的位移影响,分别建立4#和5#垂线断面坝顶测点PL4-1、PL5-1的位移统计模型,其数学表达式为

d2(lnθ-lnθ0)。

(7)

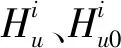
上述统计模型综合考虑了水压分量、温度分量和时效分量等因素,其中温度分量进行了周期项因子及气温资料因子的比选后,最终根据统计模型拟合效果选择周期项温度因子作为温度分量表达式,所得PL4-1、PL5-1位移统计模型的复相关系数分别为0.99、0.97,相应的模型标准差分别为0.68、0.60 mm。如图10所示,整体上所建立的统计模型拟合精度较高,模型拟合值与实测值基本吻合,较好地反映了坝体在不同环境量或运行条件下的变形规律,可用于进一步的对比分析。

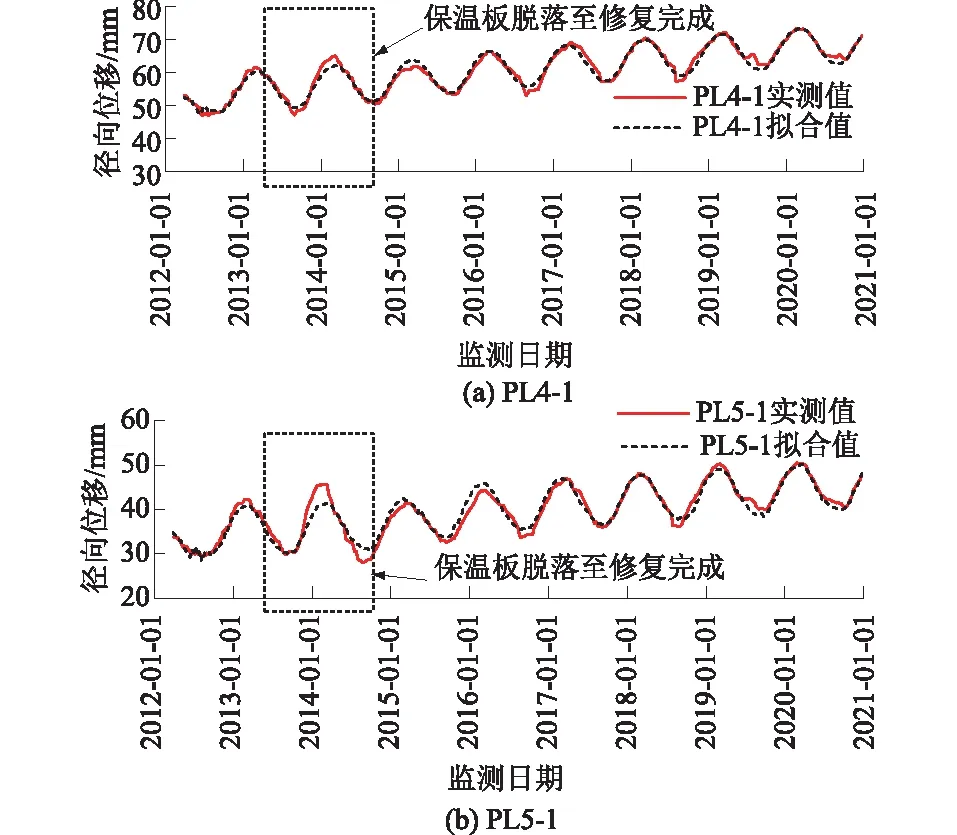
图10 坝体径向水平位移测值拟合值过程线Fig.10 Fitting values of measured radial horizontal displacement of dam body

由图10可知,2013年9月拱坝下游面保温板脱落后,通过比较保温板脱落至修复期间的统计模型拟合值与实测值可知:2013年9—10月PL4-1的径向位移向上游侧增加了3 mm,而左岸PL5-1的径向位移则相对正常;2014年1—3月PL4-1、PL5-1在温降作用下径向位移向下游侧增加了4、6 mm。对比假定保温板完好时期的模型拟合精度来看,保温板脱落期间内模型拟合值与实测值明显出现了较大偏差,该偏差可结合统计模型温度分量的建模原理分析。首先,在整个建模序列中保温板完好的监测序列较长,因此可认为该模型拟合系数主要反映了保温板完好时位移变化特征。其次,因保温板脱落导致保温板脱落时期的模型拟合值与实际温度分量变化下的实测值产生这一偏差。同时上述实测位移变化特征与图8反映的位移模拟结果趋势基本一致,进一步从监测理论分析的角度解释了保温板脱落对该拱坝位移产生的影响。

3.4 应力分析

2013年9月—2014年6月温度荷载下坝体最大主应力的分布情况如图11所示,其中拉应力为正,压应力为负。保温板完好时(2013年9月1日),温度荷载下的最大主应力出现在坝顶处。保温板脱落后,脱落区域的坝体混凝土表面温度变化增大,温度荷载下最大主应力也呈现出脱落区域大于完好区域的分布特征。此外,高温时期坝体顶部及脱落区域混凝土表面出现一定主压应力,而低温时期(3月份、12月份)相应区域则产生一定主拉应力。考虑到混凝土在温度应力下容易产生拉应力开裂,定量分析温度荷载下的坝体表面最大主拉应力:低温时期保温板脱落后,坝体下游面最大主拉应力达0.841 MPa,位于表孔下游出口区域,而脱落区域最大混凝土表面拉应力为0.451 MPa。参考该拱坝设计时的温控计算成果,其在无表面保温板保护条件下的允许拉应力为0.95 MPa。因此,可基本判断保温脱落后,坝体混凝土表面具有一定开裂风险。

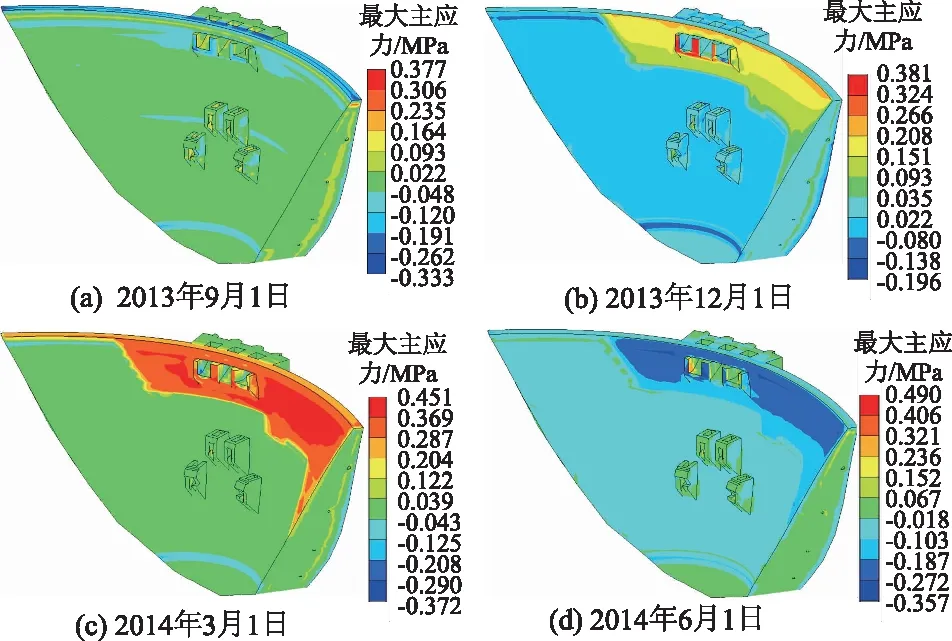
图11 温度荷载下最大主应力变化云图Fig.11 Contours of maximum principal stress under temperature load

4 结论与展望

本文以高寒地区某拱坝及保温板为研究对象,采用混凝土-保温板复合结构的等效热交换系数,从数据模拟和实测监测数据角度,对保温板脱落后的温度、位移和应力进行分析,结果表明:

(1)保温板脱落后,温度影响的区域主要为下游面混凝土,最大变化幅值可达17 ℃,实际脱落区域内部坝体混凝土温度基本稳定,无明显异常。

(2)坝体混凝土随保温板脱落后位移变化受外界气温影响具有周期性,且在脱落后的一个高低温期,位移变化显著。拱坝经历的第一个低温时期位移出现异常,左岸坝段脱落区域向下游位移的数值明显增加。同时,比较脱落区域和完好区域的特征点位移,最大位移相差2 mm。

(3)参考该拱坝设计时温度荷载下允许表面应力值范围,拱坝混凝土在无表面保温板保护条件下的允许拉应力为0.95 MPa,而基于线弹性材料本构下模拟得到的温度荷载下最大混凝土表面拉应力为0.841 MPa,在未考虑水压荷载下该数值偏小,结合设计资料综合判断,该拱坝在极端环境条件下保温板脱落后具有一定的表面混凝土开裂风险。因此,在保温板修补后,应对该部位加强监测,确保安全运行。