基于数值模型的转轮除湿系统节能优化控制研究

张 楠 姚 晔 贾东新

(1 上海交通大学机械与动力工程学院 制冷与低温工程研究所 上海 200240;2 普沃思环保科技无锡有限公司 无锡 214000)

随着人们对环境舒适度的需求不断提高,高效节能的除湿技术引起了广泛关注。与其他除湿方式相比,转轮除湿以结构紧凑、除湿效率高、能够实现连续除湿再生过程等特点[1-2],已逐渐成为空气除湿领域中的主流。

近年来,为有效解决传统除湿转轮系统能耗较高的问题,国内外学者开展了大量的研究和实验,主要从新型干燥剂材料、新型再生热源、热回收装置等方面进行[3]。何晨晨等[4]制备了MaCl2/CaCl2改性复合材料,有效提升了除湿材料的除湿能力和在低温下的脱附能力。A. Yadav等[5]研究了真空管式太阳能集热器除湿转轮在50～55 ℃范围内的再生和吸附性能。杨晚生等[6]将热空气和微波加热联合进行组合再生,实验结果表明,联合加热能够使转轮内温度分布更均匀,且能够有效提高再生率和降低能耗。杨颖等[7]通过分级再生系统利用低品位热源对转轮进行预热,在达到相同除湿效果的情况下,将再生能耗降低约50%。Yao Ye等[8-9]提出超声波能在常温、低温条件下对固体除湿剂进行再生,节能潜力较大。杨玉洁等[10]研究得出由船舶废热驱动的两级转轮除湿空调系统的节能潜力为传统空调系统的7.5%～37.6%。Sheng Ying等[11]将高温热泵和除湿转轮空调系统进行耦合,与传统蒸气压缩系统相比节约了45.6%的能耗,且在室外空气含湿量较低时节能率可进一步提升,刘异等[12]在此基础上进一步研究了高温热泵转轮除湿及辐射供冷空调系统在高温高湿地区的性能表现。陈思豪等[13]通过热力学理论分析得出室内排风回收、再生排风回收、吸附热回收和预冷处理是降低转轮除湿系统能耗的有效措施,并提出了相应的节能型转轮除湿空调系统。

然而,上述研究主要关注转轮系统本身的优化,忽略了在运行过程中环境工况实时改变的问题。针对上述问题,本文提出一种基于数值模型的转轮除湿系统节能优化控制策略。首先,构建除湿转轮数值计算模型并对其进行实验验证。在转轮模型的基础上,进一步构建转轮系统能耗模型,并以再生温度、风速、转轮转速作为优化参数,以系统能耗及除湿性能作为优化指标,建立除湿转轮系统的优化模型,采用粒子群算法(particle swarm optimization, PSO)对优化模型最优值进行求解。最后,将在优化控制策略与传统策略下的系统能耗进行对比分析,以验证优化策略的节能潜力。

1 除湿转轮数值计算模型

1.1 数学建模

除湿转轮划分为除湿区和再生区两个区域,分别通入处理空气和再生空气,通过旋转完成除湿与再生的循环过程。假设转轮内部通道规格大小均相同,在稳定工况下,任一空气通道的周期性变化也相同,彼此间仅存在相位差异,因此可以选取单一空气通道作为研究对象,以其在一个周期内不同时刻的状态变化来代表转轮稳定后在不同位置的空气通道状态。

针对单一空气通道构建沿气流方向的一维简化模型,如图1所示,以除湿转轮中一个流道为研究对象,沿空气流动方向建立z轴,沿转轮转动方向(时间方向)建立τ轴,将除湿转轮模简化为一维非稳态传热传质模型。

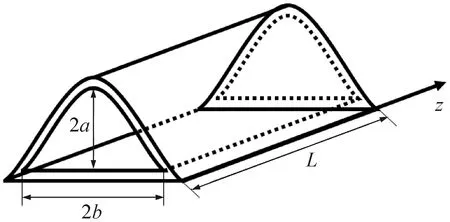
图1 除湿转轮空气通道模型

进行如下假设:

1)气流侧与固体侧均为一维,其中气流在轴向作一维层流流动;

2)多孔介质的热物性、孔径和孔隙率等参数在空间上处处相等;

3)忽略气流轴向热传导和质量扩散,并假设气流和吸湿材料的热量质量交换只通过对流完成,固体侧沿轴向发生热传导和质量扩散;

4)吸湿材料与多孔孔隙内空气的温度始终处于热平衡状态。

根据质量及能量守恒定律,建立控制方程如下:

气流侧质量平衡方程:

(1)

气流侧热量平衡方程:

(2)

吸附侧质量微分方程:

(3)

吸附侧热量微分方程:

(4)

式中:Ya为空气含湿量,g/(kg干空气);Yd为与吸附剂表面相平衡的空气的含湿量,g/(kg干空气);Ta为空气温度,K;Td为与吸附剂表面相平衡的空气的温度,K;W为吸附剂的吸附量,g/(kg吸附剂);ua为空气流速,m/s;hm为传质系数,m2/s;h为表面传热系数,W/(m2·K);P为空气通道周长,m;A为空气通道横截面积,m2;ρa、ρd分别为空气、吸附材料的密度,kg/m3;cpg、cpv、cpl、cpd分别为空气、水蒸气、液态水及吸附材料的比定压热容,J/(kg·K);qst为吸附热,J/kg。其中共有5个主要变化参数,分别Ya、Yd、Ta、Td、W。

由于空气通道为正弦曲线型,其周长和流通面积可用下式表示:

A=2ab

(5)

(6)

式中:2a、2b分别为正弦型通道的高度和宽度,m。

依据Yd、W和Td之间的相互关系将以下三个方程联立作为补充方程。

水蒸气饱和压力方程[14]:

(7)

式中:ps为水蒸气饱和蒸气压,Pa。

含湿量与相对湿度换算公式:

(8)

式中:φ为空气相对湿度;p为环境大气压,Pa。

平衡吸附曲线[15]:通过对吸附材料的吸附等温线进行拟合得到材料平衡相对湿度和吸附剂吸附量之间的关系。

(9)

式中:Wmax为吸附材料的饱和吸附量,g/(kg吸附剂);C为根据实验数据拟合的常数。

方程的初始条件及边界条件如下:

初始条件:

(10)

边界条件:

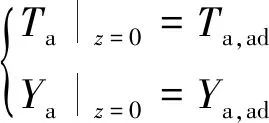
(11)

(12)

1.2 模型求解

Δy=L/Z, Δτ=T/N

(13)

对于控制方程中的偏导数,采用向后差分进行离散如下,其中,i代表空间离散点,n代表时间离散点。

(14)

1.3 模型实验验证

为验证该传热传质数学模型的可靠性,本文通过实验测试了在不同运行工况下的转轮出口工况,并与在相同工况下的数值模拟的处理空气出口温度和含湿量进行对比,实验原理及实验装置如图2所示。测量装置主要包括温度传感器、湿度传感器、速度传感器,测量精度分别为±0.2 ℃、±1%、±0.05 m/s。模拟过程中所用的转轮及物性参数如表1所示,其中吸附曲线参数由实验测量拟合。用于实验的转轮除湿系统由普沃思环保科技无锡有限公司提供。

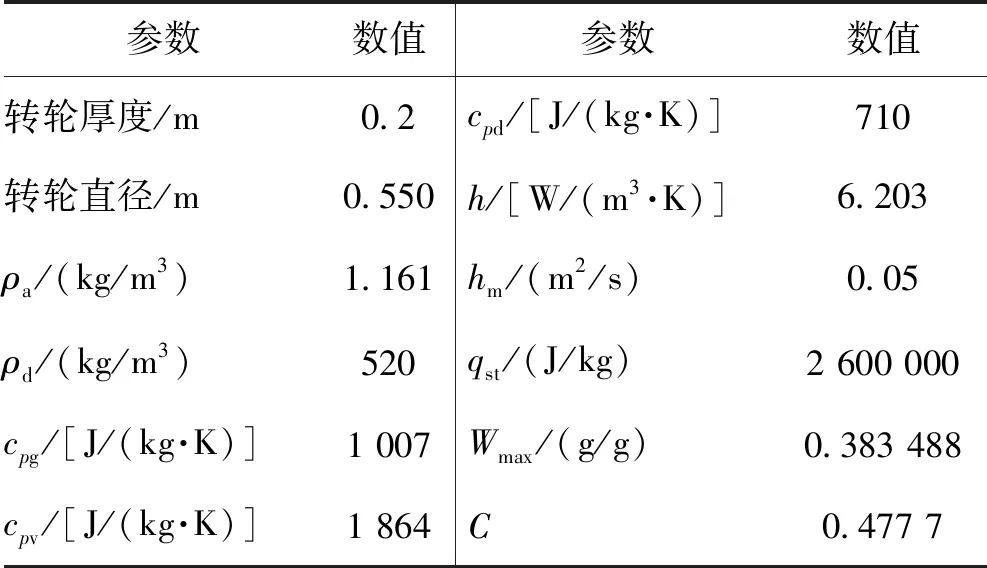
表1 模型计算参数

图2 实验原理及实验装置

在改变处理空气入口温度和含湿量的情况下,以模拟值和实验值的相对误差的绝对值作为模拟与实验的偏差来对模型计算结果和实验测量结果进行对比分析。当改变处理空气入口温度时,模拟结果与实验结果对比如图3所示,出口空气温度、含湿量的模拟值与实验值的最大偏差分别为10.2%、6.8%。当改变处理空气入口含湿量时,模拟结果与实验结果对比如图4所示,出口空气温度、含湿量的模拟值与实验值的最大偏差分别为8.3%、8.1%。由此可知,在不同工况条件下,该数学模型计算的处理空气出口温度及含湿量与实验值吻合较好,故本文所建立的除湿转轮数值模型具有可靠性。

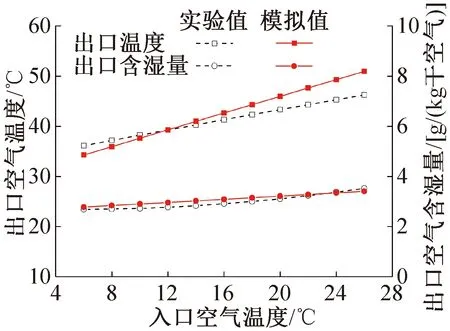
图3 入口空气温度改变时出口模拟值与实验值对比

图4 入口空气含湿量改变时出口模拟值与实验值对比

2 转轮除湿系统优化控制

2.1 优化控制模型

环境温湿度的变化对除湿转轮系统的除湿性能具有一定影响。当环境温度变化时,处理空气出口温湿度也随之改变,难以维持在设定的目标值。此外,传统除湿转轮系统通常采用恒定再生温度的工作模式,但在某些工况下,过高的再生温度会导致再生能源的浪费。为进一步提高除湿转轮的能效,使除湿转轮能够以最小的能源消耗满足除湿需求,需要对系统的实时运行进行优化控制。

为实现除湿转轮系统能够以最小的能源消耗满足除湿需求,本文根据建立的除湿转轮数值计算模型,将系统总能耗与系统除湿性能结合起来作为优化目标。根据上述分析,优化目标如下:1)除湿需求,即控制除湿转轮出口含湿量与目标设定值之间的误差在可接受范围内,该误差可通过除湿转轮数值模型计算而得;2)最小能耗,即控制系统总能耗在最小值,其中系统总能耗需进一步建立能耗模型进行计算。

在除湿转轮系统中,能耗主要来自两部分:再生能耗以及风机能耗。

再生能耗:

Ereg=cpgρaAregureg(Ta,reg-Ta,ad)

(15)

式中:Areg为再生面积,m2;ureg为再生空气风速,m/s;Ta,reg为再生温度,K;Ta,ad为环境温度,K。

风机能耗包括处理风机能耗Efan,ad和再生风机能耗Efan,reg:

(16)

(17)

式中:pfan为风机全压,Pa;Gad为处理空气风量,m3/s;Greg为再生空气风量,m3/s;K为电动机容量储备系数;η为效率。

故系统总能耗模型:

Etotal=Ereg+Efan,ad+Efan,reg

(18)

引入权值因子λ对两个优化目标进行归一化处理,λ越小,对出口含湿量的误差要求越高,λ越大,则越追求更低能耗,对出口含湿量误差的要求也相应放低。归一化的优化目标函数即优化算法的适应度函数:

J=λEtotal+(1-λ)(Ya,out-Ya,ref)2

(19)

式中:λ为权值因子,λ∈[0,1];Etotal为系统总能耗,kW;Ya,out为处理空气出口含湿量,g/(kg干空气),可通过除湿转轮数值模型计算获得;Ya,ref为处理空气出口含湿量设定值,g/(kg干空气)。

确定优化目标后,还需要对优化参数进行分析。根据前述建立的除湿转轮数值模型可知,除湿转轮系统具有多种变量,包括处理空气相关参数、再生空气相关参数、转轮相关参数等。其中,部分变量属于不可控变量,如环境温度、环境含湿量、转轮厚度、转轮材料等。虽然这些变量对系统的除湿性能有一定影响,但由于在实际控制时,难以对这些变量进行调整和修改,因此,在优化控制过程中,该部分参数会根据实际情况设定为常数。而另一部分变量,如再生温度、处理风速、再生风速、转轮转速等可以通过调节电加热时间、风机、电机等进行直接控制,其中,处理风速在需要保证除湿空气风量的场景下需保持为定值,因此,本文将再生温度Ta,reg、再生风速ureg、转轮转速r这三个变量作为优化参数。

由于风机、电机等在正常运行过程中具有工况限制,其对应的变量也存在相应限制,故对优化变量提出如下合理约束条件:

(20)

综合适应度函数以及约束条件,除湿转轮系统实时运行优化问题如下:

(21)

2.2 优化模型求解

针对所建立的优化控制模型,本文采用改进PSO算法进行模型求解。PSO是一种模拟自然界生物群体智能的随机优化算法,具有收敛快速、参数调节灵活、易于实现等优点[16]。在搜索过程中,PSO算法结合个体认知和社会影响对粒子速度和位置进行不断更新,进而寻求最优值。

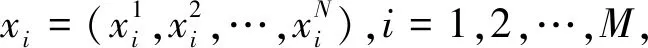
(22)

由于在基本PSO算法中,若ω赋值过大,会导致粒子局部搜索能力太低,导致搜索精度不足;ω赋值过小,会导致粒子全局搜索能力不足,容易陷入局部最优。因此,ω不宜为固定常数。本文采用改进PSO算法,通过自适应调整策略使ω惯性权重线性减小,进而使算法在前期具有较强的全局搜索能力,使搜索空间能够快速收敛至某一区域,在后期则有较强的局部搜索能力,提高搜索精度[17]。改进的惯性权重如下:

(23)

式中:ωmax为最大惯性权重;ωmin为最小惯性权重;I为当前迭代次数;Imax为最大迭代次数。

基于上述改进PSO,对除湿转轮系统实时运行优化问题进行计算求解。环境温湿度改变后,除湿转轮出口含湿量及系统总能耗也随之发生变化,进而导致目标函数值变化,此时采用改进PSO算法对新环境工况下的最优目标函数值进行求解计算,并返回优化后的可控变量:再生温度、再生风速以及转轮转速,从而实现除湿转轮系统的实时优化控制。整个优化控制流程如图5所示。

图5 除湿转轮系统实时运行优化策略

其中PSO优化过程具体步骤如下:

1)参数初始化,如粒子群规模、粒子维度、迭代次数、惯性权重、学习因子等。

2)根据变量约束范围,随机初始化各粒子的速度及位置,并根据除湿转轮模型和能耗模型计算得到出口含湿量和总能耗,随后根据适应度函数计算得到各粒子的初始适应值。

3)确定各粒子的最优适应值为初始适应值,对比各粒子适应值大小获取种群最优适应值,并确定个体及种群最优适应值所对应的位置。

4)根据式(23)对惯性权重进行更新。

5)根据式(22)对各粒子速度及位置进行更新,并根据转轮模型和能耗模型计算其适应值。

6)对比各粒子当前适应值与个体最优适应值的大小,若该粒子当前适应值小于个体最优适应值,则更新该粒子的最优适应值为其当前适应值,并更新该粒子的个体最优位置。对比所有粒子当前适应值与种群最优适应值的大小,若某粒子当前适应值小于种群最优适应值,则更新种群最优适应值为该粒子当前适应值,并更新种群最优位置。

7)判断是否达到设定的最大迭代次数,否则返回步骤4),是则输出种群最优适应值及其所对应的位置。

3 结果与分析

由式(19)可知,权值因子λ决定了转轮除湿系统的能耗指标与除湿性能指标在优化过程中的占比权重,不同的λ会导致不同的优化结果。在同一初始条件下,λ越大,能耗指标占比越大,能耗优化效果越好,但出口含湿量与目标设定值的偏差也更大,λ越小,出口含湿量与目标设定值越接近,除湿性能越好,但能耗优化效果降低。因此,需要探究不同λ下的优化策略的有效性。

本文在不同环境温度Ta,ad及环境含湿量Ya,ad工况下,将λ从0均匀增至1,计算在优化策略下的出口含湿量和能耗优化值,并与传统策略能耗及目标含湿量进行对比。在传统控制策略中,再生温度和再生风速根据需求设置为定值。计算中采用的PSO算法初始化参数总结如表2所示。

表2 PSO算法初始化参数

3.1 不同环境含湿量下优化性能对比

在保持环境温度Ta,ad为27 ℃的条件下,改变环境含湿量Ya,ad及权值因子λ,计算优化策略下的能耗节省率εE及出口含湿量控制误差εYa,其中Ya,ad变化范围为16～22 g/(kg干空气),λ权值因子变化范围为0～1。优化结果及相应优化参数如图6所示。

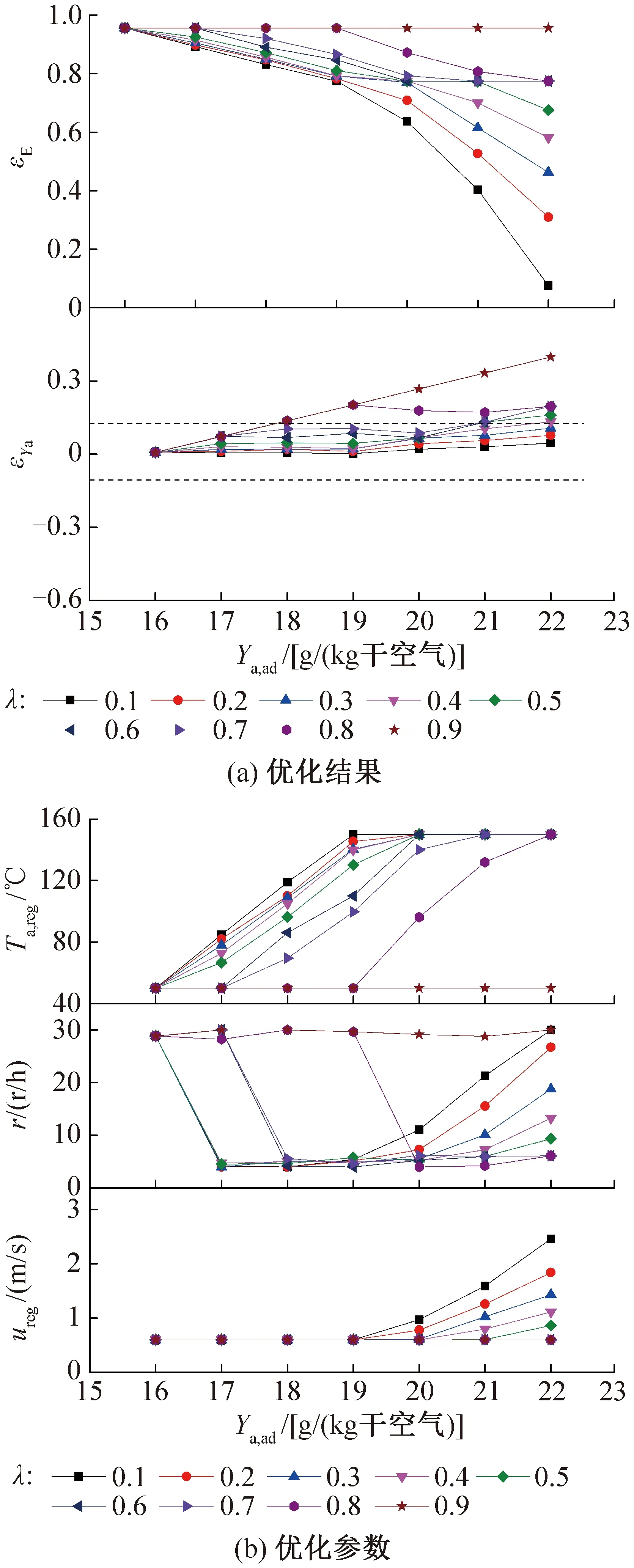
图6 不同环境含湿量下的优化性能

图6(a)所示为在不同Ya,ad和λ下εE及εYa的变化情况。从整体来看,εYa随着Ya,ad和λ的增大而增大,εE随着λ的增大而增大,但随Ya,ad的增大而降低,且降低速率逐渐增大。

对于εYa,要求在不同Ya,ad下的εYa均可控制在10%范围内。当λ<0.3时,不同Ya,ad下的εYa变化缓慢,均控制在10%范围内。当λ>0.3时,随着λ和Ya,ad的增大,εYa也不断增大,在高环境含湿量下εYa超过10%,不能满足除湿要求。这是因为当λ<0.3时,在优化过程中除湿性能指标的占比更大,此时对除湿出口控制误差要求更为严苛,因此不同Ya,ad下出口含湿量均可控制在要求范围内。而当λ>0.3时,随着λ权值因子和Ya,ad的增大,除湿性能指标占比降低且所需除湿量增大,因此在高环境含湿量下εYa无法控制在要求范围之内。因此λ应控制在0～0.3范围内。

对于εE,在满足εYa小于10%的前提下,εE越高越好。在低环境含湿量下,εE均能维持在较高范围内,达70%以上,而在高环境含湿量下,εE较低,但随λ的增大而增加。这是因为在低环境含湿量下,所需除湿量较低,所需的再生温度及再生风速也较低,εE较高,而在高环境含湿量情况下则需要较高的再生温度才能满足除湿要求,因此εE较低,但可通过增大λ来增加能耗指标占比以提高εE。因此在λ=0.3时,既能满足出口含湿量要求,又能使εE达到最高。此时,εYa最高为9.6%,εE在环境含湿量为16 g/(kg干空气)时达到最高值95.6%,在环境含湿量为22 g/(kg干空气)时为最低值46.3%,平均εE为76.4%。

图6(b)所示为在不同环境含湿量Ya,ad和权值因子λ下的优化再生风速ureg、转速r及再生温度Ta,reg。由图可知,在低环境含湿量下,主要通过减小Ta,reg对能耗进行优化,在高环境含湿量下,主要通过调节r及ureg对能耗进行优化。

3.2 不同环境温度下优化性能对比

在保持环境含湿量Ya,ad为19 g/(kg干空气)的条件下,改变环境温度Ta,ad及权值因子λ,其中Ta,ad变化范围为24～30 ℃,λ变化范围为0～1。优化结果及相应优化参数如图7所示。

图7 不同环境温度下的优化性能

图7(a)所示为在不同Ta,ad和λ下能耗节省率εE及出口含湿量控制误差εYa的变化情况。由图可知,随着Ta,ad增加,εYa均无明显变化,当λ<0.7时,εYa均控制在10%范围内。εE在λ较小时呈随Ta,ad增加而轻微下降趋势,在λ较大时则无明显变化。这是因为Ta,ad的改变对除湿性能的影响主要通过物性参数及传热传质性能,因此随Ta,ad增加,εYa无明显变化,但所需再生温度轻微增加,导致εE随之轻微下降。在λ=0.7时,Ta,ad在24～30 ℃范围内,最高εE为42.1%,最低εE为36.0%,平均εE为40.2%。

图7(b)所示为在不同环境温度Ta,ad和权值因子λ下的优化再生风速ureg、转速r及再生温度Ta,reg。由图可知,在不同Ta,ad下,r及ureg无明显变化,Ta,reg随Ta,ad的增加而轻微增加。

4 结论

本文提出一种基于数值模型的转轮除湿系统节能优化控制策略方法,在转轮模型和能耗模型基础上,通过引入权值因子把系统能耗及除湿性能相结合作为优化指标,构建转轮除湿优化模型。该模型以再生温度、再生风速、转轮转速作为优化参数,以改进PSO作为优化算法,并将不同环境温度和含湿量下的优化控制结果和传统策略结果进行对比,得到如下结论:

1)优化控制要求为将出口含湿量控制误差控制在10%以内。为满足该要求,当环境温度控制在27 ℃,环境含湿量在16～22 g/(kg干空气)区间内变化时,权值因子λ应小于0.3;当环境含湿量控制在19 g/(kg干空气),环境温度在24～30 ℃区间内变化时,权值因子λ应小于0.7。

2)优化控制目标为在满足出口含湿量控制误差要求基础上尽可能降低能耗节省率。随着环境含湿量升高,能耗节省率逐渐降低,且降低速率逐渐增大。环境含湿量在16～22 g/(kg干空气)范围内,平均能耗节省率为76.4%。当权值因子λ=0.3时,环境含湿量为16 g/(kg干空气)时能耗节省率达到最大值95.6%。

3)随着环境温度升高,能耗节省率轻微下降,同时在环境温度大于28 ℃、权值因子大于0.6时存在波动。环境温度在24～30 ℃范围内,平均能耗节省率为40.2%。当权值因子λ=0.7时,环境温度为24 ℃时能耗节省率达到最大值42.1%。