轮盘低周疲劳模拟件设计及试验

赵淼东，胡殿印，毛建兴，孙海鹤，秦仕勇，古远兴，王荣桥，3，4，*，田腾跃，鄢林，肖值兴

1.北京航空航天大学 能源与动力工程学院，北京 100191

2.北京航空航天大学 航空发动机研究院，北京 100191

3.北京航空航天大学 航空发动机结构强度北京市重点实验室，北京 100191

4.中小型航空发动机联合研究中心，北京 100191

5.中国航空发动机集团有限公司 四川燃气涡轮研究院，成都 610500

轮盘作为军用航空发动机关键件、民用航空发动机中限寿件，长时间在交变大载荷下工作，轮盘结构中常存在盘心、螺栓孔、端齿等应力集中的特征部位，因此容易发生低周疲劳失效［1］。为了准确评估轮盘特征部位的疲劳寿命，针对这些特征部位设计反映应力梯度的模拟件，并开展疲劳试验是十分必要的［2］。

轮盘模拟件设计的核心是保证模拟件的疲劳寿命与轮盘考核部位一致。现有的模拟件设计方法通常是基于某种结构寿命预测理论提出的。例如，基于经典的名义应力法［3-4］和局部应力应变法［5-6］等一系列模拟件设计方法。由美雁等［7］基于局部应力应变法，提出了“最大主应力、应力分量、应力梯度与考核部位一致”的轮盘模拟件设计方法。魏大盛等［8］在轮盘模拟件设计过程中，保证了模拟件危险点的多轴应力、应力梯度与考核部位一致。刘廷毅等［9］提出了“最大应力、最大主应力梯度一致”的设计方法。赵福星等［10］引入应变分布影响系数设计轮盘模拟件。近年来，基于这些方法设计的模拟件被广泛用于轮盘及航空发动机中其他重要部件的寿命考核中［11-13］。上述方法保证了模拟件危险点的损伤控制参量（如最大主应力、最大主应变、应力梯度等）与轮盘考核部位相一致。

然而，已有研究表明［14-17］，考虑应力梯度对结构疲劳寿命的影响不仅与危险点的应力、应变大小有关，还与危险点附近“一定范围内”的应力、应变分布有关。相应地，发展了基于非局部寿命理论的模拟件设计方法。陆山等［18］提出的轮盘模拟件设计方法中，考虑了危险点最大主应力在其梯度方向的分布。杨兴宇［19］、郑小梅［20］等提出了工程裂纹长度范围内（0.8 mm）的主应力、主应变、主应变弹塑性分量一致的轮盘模拟件设计方法。SU等［21］在von Mises等效应力、应力梯度一致的准则基础上，提出了等效有害体积一致的设计准则。但这些方法对“一定范围”的定义缺乏理论依据且未能形成统一认识。如果这一范围过小，难以保证模拟件与真实结构考核部位的疲劳寿命一致；若范围过大，则会导致模拟件尺寸过大，给试验的加载与夹持带来困难，增加了设计难度。

目前，临界距离法被广泛用于应力集中部位的疲劳寿命预测［22-24］，认为应力集中部位临界距离内的应力、应变均对结构疲劳寿命产生影响，据此建立了临界距离的求解方法［25-29］。基于此，本文以经典的SWT模型（Smith-Watson-Topper Model）［30-32］的 损 伤 参 量——SWT参 量为准则，提出了一种基于临界距离内SWT参量一致的轮盘模拟件设计方法。以某型航空发动机高压涡轮盘为例，开展了涡轮盘的盘心、螺栓孔、端齿等特征部位的模拟件设计，并进行了相应的模拟件低周疲劳试验。在此基础上，进行了真实高压涡轮盘的旋转疲劳试验，验证轮盘模拟件的设计方法。最后，讨论了该模拟件设计方法的稳健性。

1 轮盘低周疲劳模拟件设计方法

1.1 考虑应力集中的低周疲劳寿命预测方法

本研究中，材料低周疲劳寿命预测采用了多轴形式下的SWT模型［30-31］，其表达式为

式中：Δε1为最大主应变范围；σn，max为最大主应变所在平面的最大正应力；E为弹性模量；Nf为疲劳寿命；σ′f、ε′f、b、c为材料参数。

上述模型中，等式左边为影响疲劳寿命的因素，由加载的应力与应变决定，称为SWT参量，记为PSWT，则

采用临界距离理论反映应力梯度对疲劳寿命的影响，常用的计算式为

式中：Pm为平均后的SWT参量；L为临界距离；α、β为材料参数。将Pm代入式（1），替换其中的SWT参量PSWT，表达式为

联立式（3）～式（5），可求得临界距离。

1.2 轮盘模拟件设计准则与方法

本文提出了一种基于SWT参量一致的轮盘模拟件设计方法，其中涉及的设计准则包括：

1）几何相似性：模拟件考核部位的几何形状应当与真实轮盘的考核部位相似。具体地，应保证模拟件的关键尺寸（如盘心的直径、螺栓孔的倒角尺寸、端齿的形状等）与真实轮盘一致。

2）材料一致性：一般地，模拟件应从真实轮盘毛坯上取样，且取样位置保持一致，并通过取向选择保证其受力方向与真实轮盘的考核部位一致。

3）SWT参量一致性：保证临界平面上临界距离范围内的SWT参量分布与真实轮盘一致。

基于上述设计准则，开展轮盘模拟件设计，具体步骤如下：

1）开展真实轮盘的有限元分析，以SWT参量最大点作为危险部位，以最大主应变所在的平面为临界平面，以临界平面上SWT参量的负梯度方向作为考核路径方向，提取SWT参量分布。在此基础上，根据式（3）～式（5）确定临界距离。

2）根据准则2），以真实轮盘的材料及对应温度下的材料性能作为模拟件有限元计算的输入。根据准则1），确定盘心的直径、螺栓孔的倒角尺寸、端齿的形状等作为关键尺寸，保证这些关键尺寸与真实轮盘一致。在此基础上，开展有限元分析，用步骤1）中相同的方法确定考核路径方向，提取模拟件的SWT参量分布。

3）根据准则3），通过添加槽、开口，改变缺口深度等辅助特征调整模拟件考核部位临界平面上的SWT参量分布，在临界距离范围内使之与真实轮盘一致。在此基础上设计夹持段，使其具有足够的强度储备。

2 轮盘模拟件设计实例

以某型航空发动机高压涡轮盘为例，开展模拟件设计。

首先，通过服役条件下涡轮盘的有限元分析，确定考核部位。根据涡轮盘的结构特征，分别建立了含有榫槽和叶片的1/73扇区有限元模型A与含有端齿、螺栓孔的1/12扇区有限元模型B（如图1所示）。模型A简化了端齿、螺栓孔等细节，并为模型B提供截面的径向位移；模型B在前轴颈部位沿周向剖开。涡轮盘的材料为FGH96，叶片材料为DD6，其材料性能参数见表1。服役状态下，从涡轮盘盘心到涡轮叶片的温度变化范围为400～900 ℃。转速为14 000 r/min。

表1 涡轮盘与叶片材料力学性能参数Table 1 Mechanical properties of turbine disc and blade materials

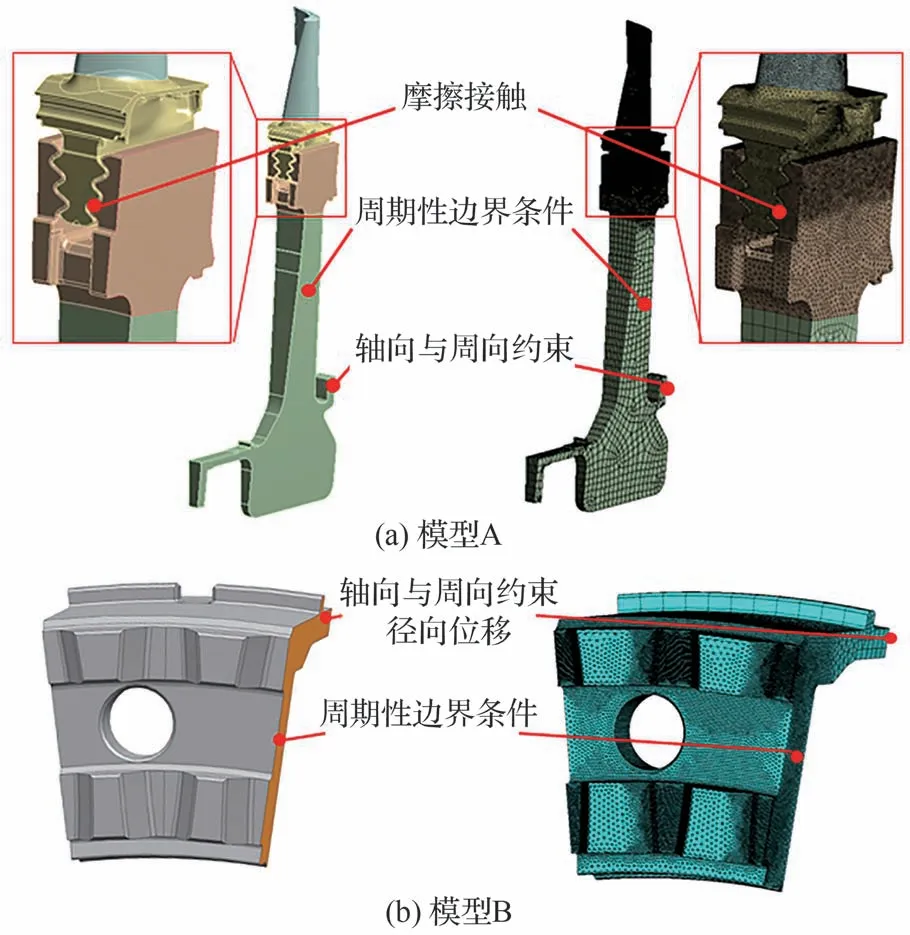
图1 涡轮盘有限元模型Fig.1 Finite element model of turbine disc

有限元模型A的边界条件包括：①榫槽部位与叶片榫头的接触面为摩擦接触，摩擦系数为0.2；②扇区的循环对称面为周期性边界条件；③后轴颈端面为轴向与周向位移约束。

有限元模型B的边界条件包括：①截面径向位移大小由模型A决定，约束轴向与周向的位移；②扇区的循环对称面为周期性边界条件。

有限元模型A与模型B的最大主应变分布如图2所示。由1.1节确定涡轮盘的SWT参量分布。选择应力集中明显的盘心、螺栓孔、端齿作为危险部位（见图3），设计相应的模拟件。上述部位温度均低于550 ℃，该温度下，FGH96的蠕变损伤相比疲劳损伤不显著，因此上述部位的蠕变-疲劳失效问题暂不考虑。

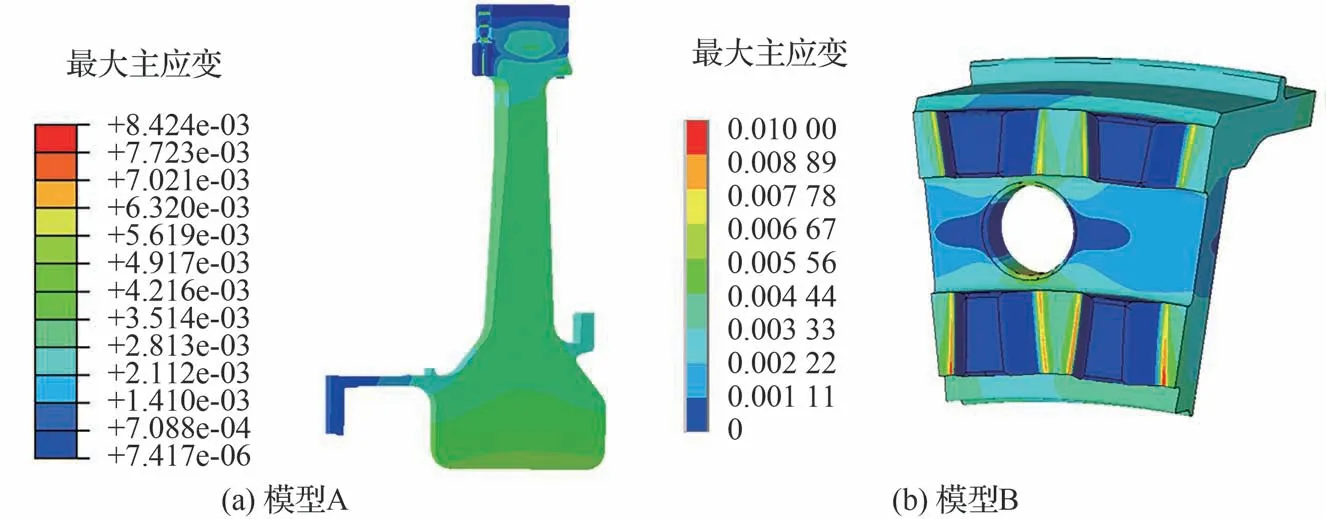
图2 涡轮盘最大主应变分布Fig.2 Maximum principal strain distribution of turbine disc

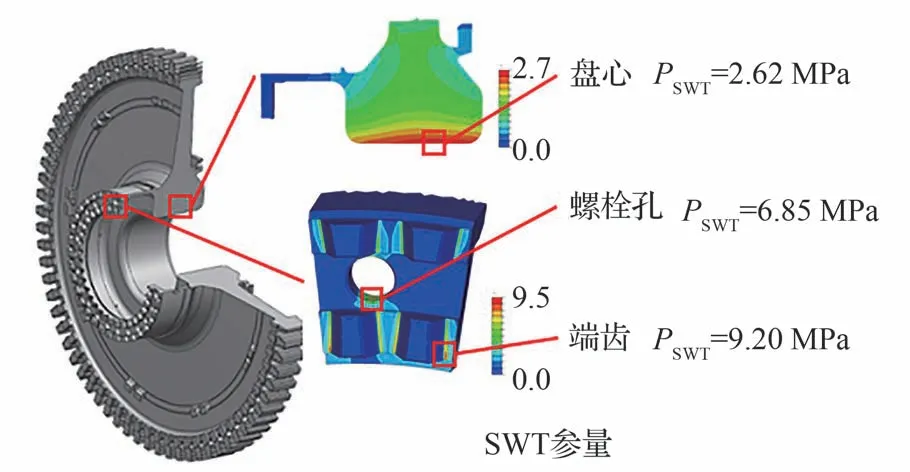
图3 涡轮盘形状与危险部位Fig.3 Shape and dangerous locations of turbine disc

2.1 盘心模拟件设计

根据盘心部位有限元分析的结果，以步骤1）所述的方式，提取盘心部位的SWT参量分布。根据临界距离法的计算公式（式（3）～式（5）），计算临界距离为0.91 mm。

盘心模拟件的考核部位采用圆弧缺口形式（见图4），选择圆弧半径RPX为关键尺寸，保证其与盘心的半径一致。该设计方案中包括2个可调整的几何参数：距离中心线的半宽度WPX和圆弧深度DPX。开展模拟件的有限元分析，并优化上述的几何参数，使模拟件的考核部位临界距离范围内的SWT参量与真实结构的一致。这一过程中，往往存在着多种几何参数的组合满足临界距离范围内SWT参量一致性的设计准则。为了提高效率，采用的策略是选择对SWT参量分布影响最大的几何参数进行单变量优化。具体步骤为：

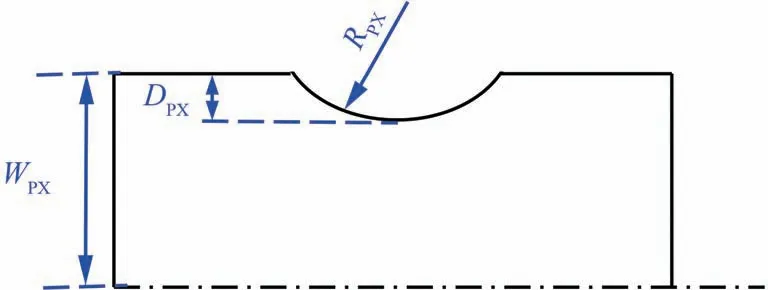
图4 盘心模拟件结构形式Fig.4 Configuration of simulating specimen for turbine disc bore

1）调整上述的几何参数，分析各几何参数对归一化的SWT参量的影响。定义路径上距离为x位置的归一化的SWT参量pSWT为该点SWT参量与路径初始点的比值，如式（6）所示：

几何参量分别取初始值的90%和110%，分别计算临界距离范围内的归一化的SWT参量。将临界距离范围内两者最大差值与（110%-90%）的比值定义为几何参数对SWT参量的敏感性s，如式（7）所示：

s越大的几何参数，对模拟件SWT参量分布影响越大。选择其中敏感性最大的参数进行单变量优化。

2）确定步骤1）中所选择的几何参数以外的其他几何参数的取值，以满足试验件结构紧凑、试验载荷大小适宜的目的，适应试验条件，便于开展低周疲劳试验。

3）调整步骤1）中所选择的几何参数，直到模拟件临界距离范围内SWT参量分布与真实结构的一致。定义模拟件与真实构件的SWT参量分布误差e为临界距离范围内两者SWT参量最大差值与真实构件最大SWT参量的比值，如式（8）所示：

本研究采用的容差为10%，当SWT参量分布误差e小于容差时，认为模拟件临界距离范围内SWT参量分布与真实结构的一致。

半宽度WPX与圆弧深度DPX的敏感性s如图5所示，其中下标“0”为参数敏感性分析的参考值。对比二者的敏感性可知，WPX对SWT参量分布的影响更显著，因此对WPX进行单变量优化。通过参数优化，确定的模拟件考核段尺寸见图6。此时，盘心模拟件的最大主应变分布如图7所示。盘心模拟件与真实轮盘SWT参量分布对比如图8所示，在临界距离范围内，最大误差不超过1%。

图5 盘心模拟件几何参数敏感性对比（WPX0=10 mm，DPX0=2.5 mm）Fig.5 Comparison of sensitivity of geometrical parameters of simulating specimen for turbine disc bore （WPX0=10 mm， DPX0=2.5 mm）

图6 盘心模拟件考核段尺寸Fig.6 Test section size of simulating specimen for turbine discs bore

图7 盘心模拟件最大主应变分布Fig.7 Maximum principal strain distribution on test section of simulating specimen for turbine disc bore

图8 盘心模拟件与真实盘心部位的SWT参量对比Fig.8 Comparison of SWT parameter distribution between hotspots of simulating specimen and turbine disc bore

随后，设计模拟件的夹持段与过渡段。夹持段采用平板摩擦夹持的设计方案，宽度与厚度均大于考核段，夹持段与考核段通过圆弧链接。图9为盘心模拟件尺寸。

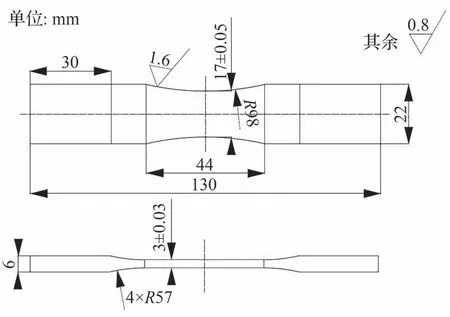
图9 盘心模拟件尺寸Fig.9 Design result of simulating specimen for bore

最后，从真实涡轮盘毛坯的盘心位置处周向取样并进行加工，其中盘心模拟件考核部位与涡轮盘盘心处的粗糙度保持一致。采用MTS370.10型电液伺服疲劳机开展低周疲劳试验，试验温度为500℃，加载频率为10 Hz。试验条件见表2。考虑到试验夹具的具体情况，为了避免载荷比R=0时因间隙而控制不稳的情况，将载荷比为R=0的试验条件调整为R=0.05。盘心模拟件的低周疲劳试验结果见图10。

表2 盘心模拟件低周疲劳试验条件（500 ℃）Table 2 Conditions of fatigue experiment for simulating specimen of bore at 500 ℃

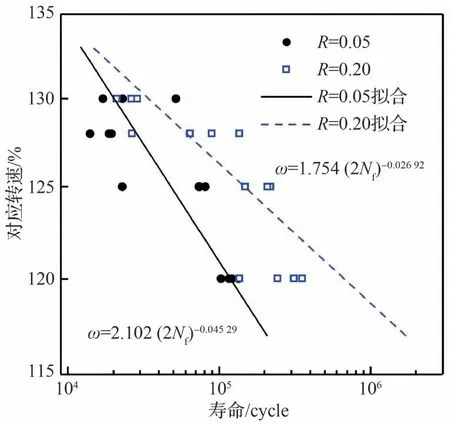
图10 盘心模拟件低周疲劳试验结果Fig.10 Results of fatigue experiment for simulating specimen of bore

结果表明，所有盘心模拟件均从考核部位处断裂（图11），证明了试验的有效性。由图12所示的SEM断口观测结果可见，盘心模拟件从加工表面起裂（箭头指示位置为裂纹源）。

图11 试验后的盘心模拟件照片Fig.11 Photo of simulating specimen of bore after experiment

图12 盘心模拟件断口观测Fig.12 Fracture morphology of simulating specimen of bore

2.2 螺栓孔模拟件设计

同前所述，根据有限元分析的结果，以步骤1）所述的方式，提取螺栓孔部位的SWT参量分布。根据临界距离法的计算公式（式（3）～式（5）），计算临界距离为1.27 mm。

螺栓孔模拟件采用圆孔平板+两侧半圆缺口的基本形式（见图13），中心圆孔处设置倒角以模拟真实轮盘螺栓孔的结构特征。该设计方案选择了试验件厚度HLSK，圆孔孔径DLSK，孔倒角CLSK为关键尺寸，分别与真实轮盘螺栓孔部位的厚度、螺栓孔直径、螺栓孔倒角一致。设计方案中包括3个可调整的几何参数：两侧圆弧半径rLSK、圆弧距中心距离cLSK及试验件宽度WLSK。开展模拟件的有限元分析，对比上述几何参数的敏感性（见图14，其中下标“0”为参数敏感性分析的参考值），选择对SWT参量分布影响最大的试验件宽度WLSK作为优化变量开展优化，使模拟件的考核部位临界距离范围内的SWT参量与真实结构的一致。通过参数优化，螺栓孔模拟件的最大主应变分布见图15，螺栓孔模拟件与真实轮盘SWT参量分布对比见图16。在临界距离范围内，最大误差不超过1.8%。

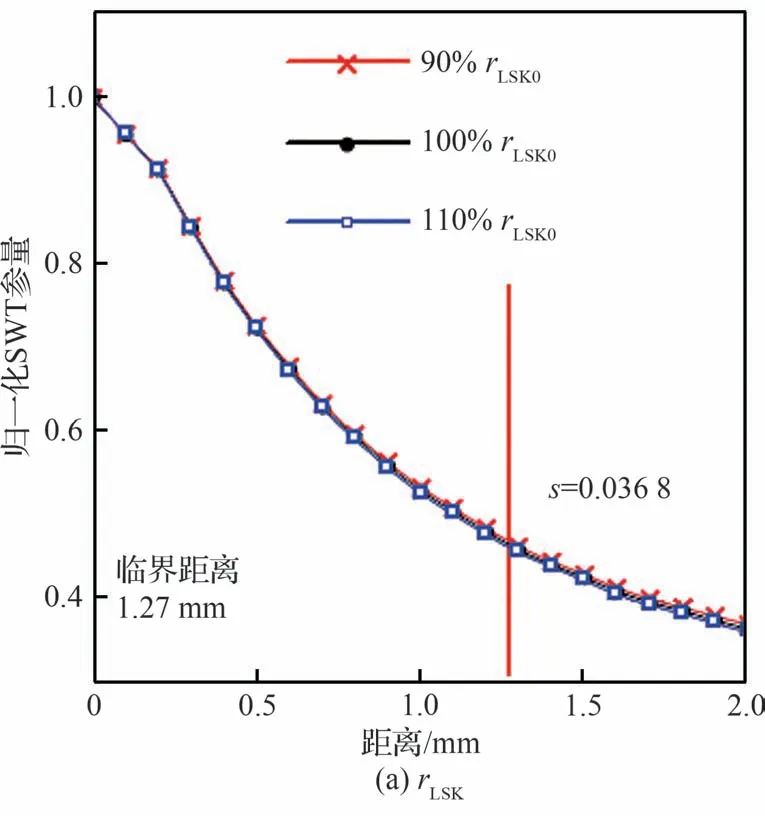
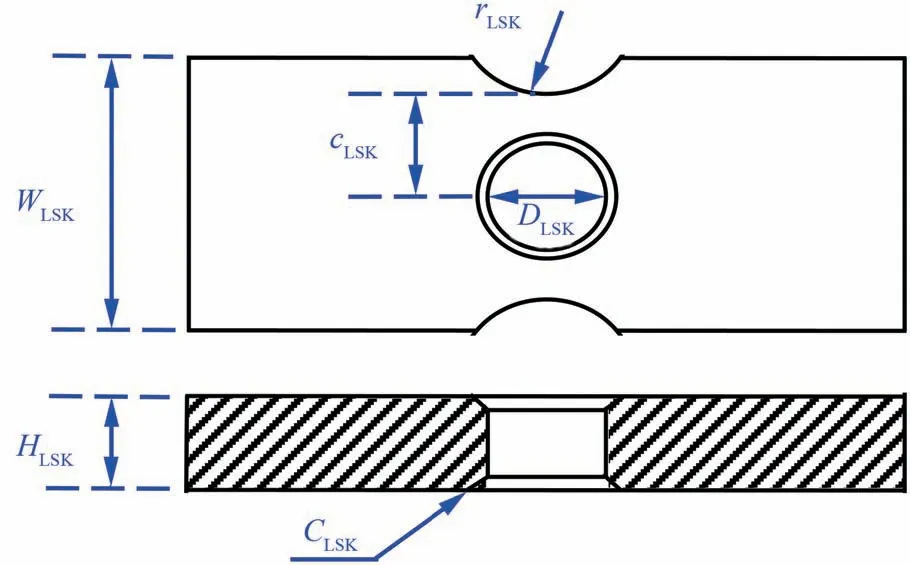
图13 螺栓孔模拟件结构形式Fig.13 Configuration of simulating specimen for bolt hole of turbine disc

图15 螺栓孔模拟件最大主应变分布Fig.15 Maximum principal strain distribution of simulating specimen for turbine disc bolt hole

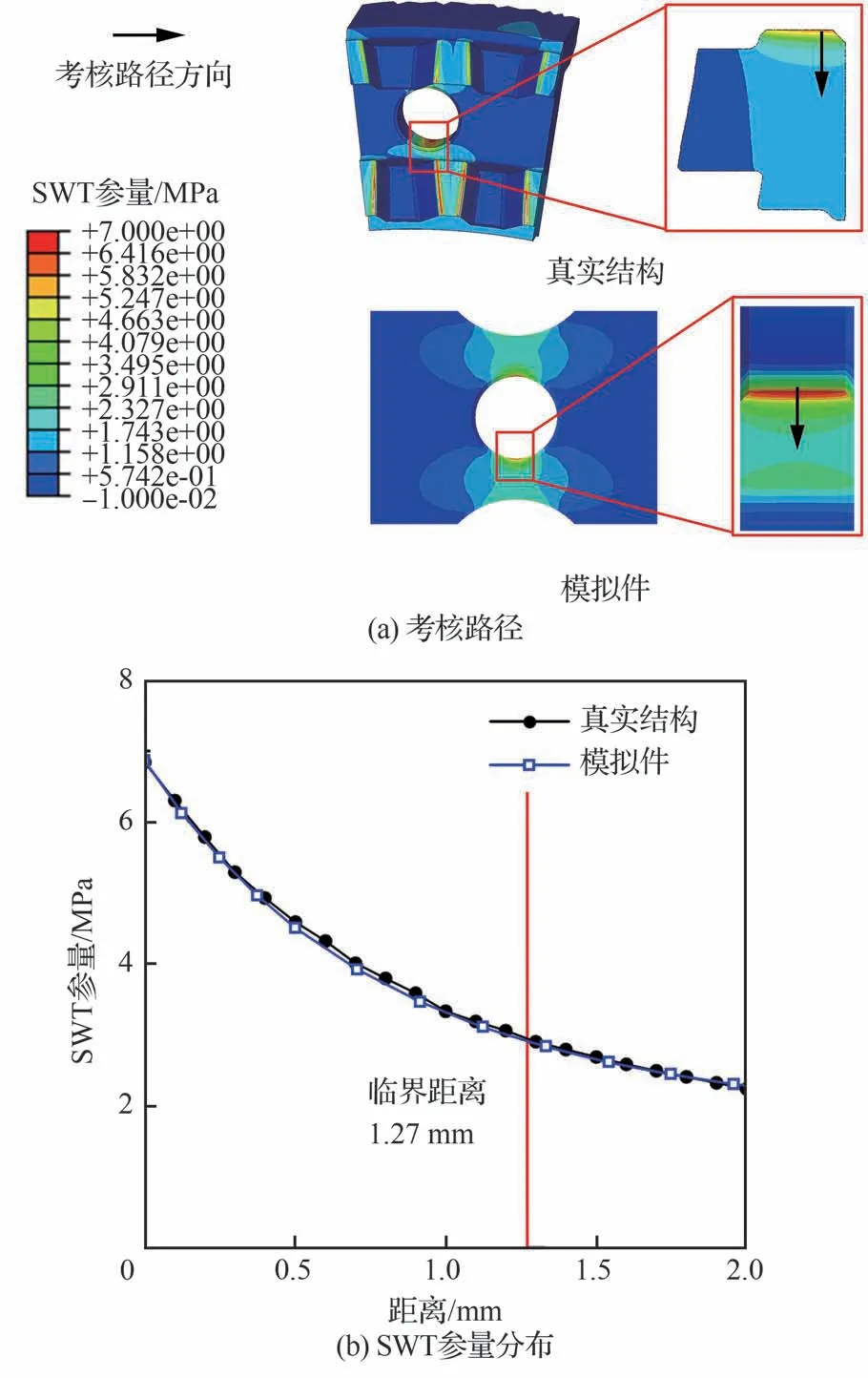
图16 螺栓孔模拟件与真实螺栓孔部位SWT参量对比Fig.16 Comparison of SWT parameter distribution between hotspots of simulating specimen and turbine disc bolt hole

随后，设计模拟件的夹持段与过渡段。夹持段采用摩擦夹持的方案。螺栓孔模拟件设计结果见图17。

图17 螺栓孔模拟件设计结果Fig.17 Design result of simulating specimen for bolt hole

最后，从真实涡轮盘的前轴颈部分周向取样并进行加工，其中螺栓孔模拟件的考核部位与涡轮盘螺栓孔部位粗糙度保持一致。开展螺栓孔模拟件的低周疲劳试验，试验温度为550 ℃，加载频率为5 Hz，试验条件见表3。这里同样根据夹具的加载能力，将载荷比R=0的情况调整为R=0.05。试验设备与试验流程与2.2节中一致。试验结果见图18。

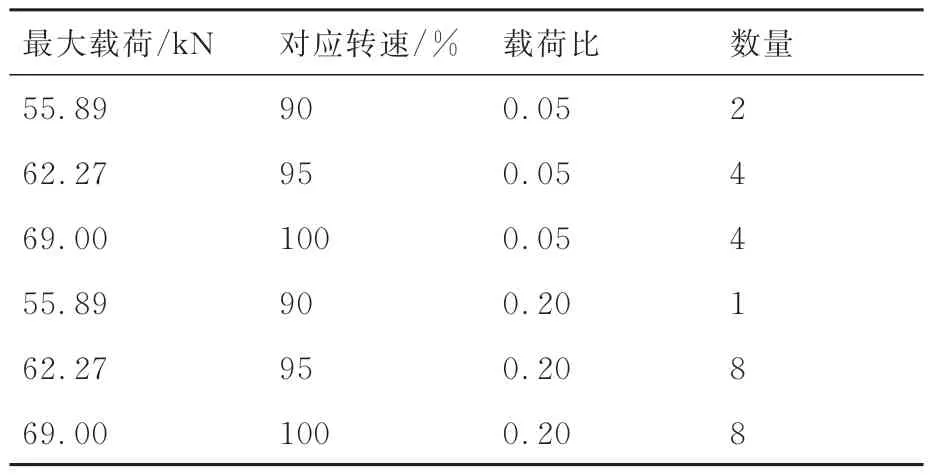
表3 螺栓孔模拟件低周疲劳试验条件（550 ℃）Table 3 Condition of fatigue experiment for bolt hole’s simulating specimen at 550 ℃

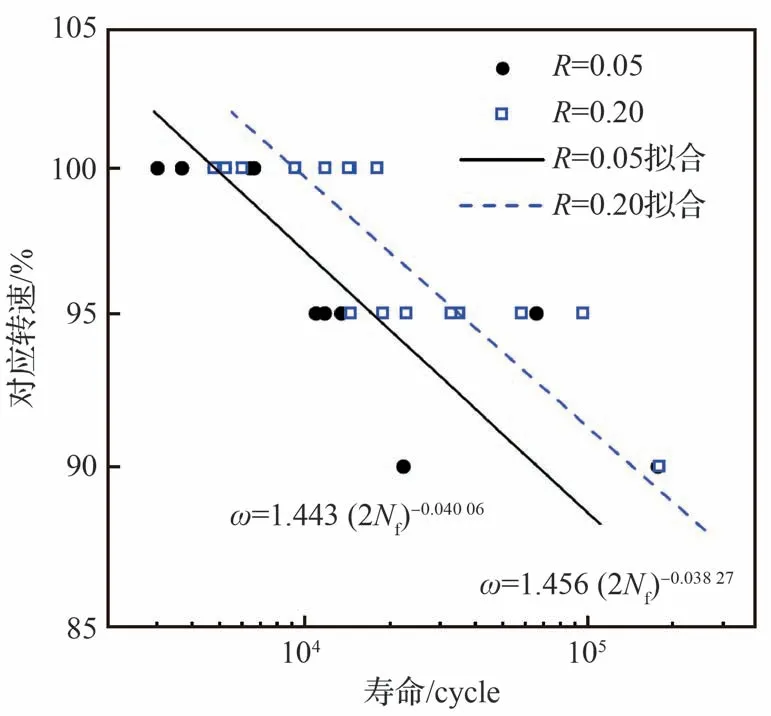
图18 螺栓孔模拟件疲劳试验结果Fig.18 Results of fatigue experiment for bolt hole simulating specimen

所有螺栓孔模拟件均从考核部位断裂（见图19）。由图20所示的SEM断口观测结果可见，螺栓孔模拟件均从孔边起裂（箭头指示位置为裂纹源），以表面裂纹形式扩展。

图19 试验后的螺栓孔模拟件照片Fig.19 Photo of bolt hole simulating specimen after experiment

图20 螺栓孔模拟件断口观测Fig.20 Fracture morphology of bolt hole simulating specimen

2.3 端齿模拟件设计

同前所述，根据有限元分析的结果，以步骤1）所述的方式，提取螺栓孔部位的SWT参量分布。根据临界距离法的计算公式（式（3）～式（5）），计算临界距离为0.79 mm。

端齿模拟件采用带对称凸台与凹槽的平板为基本形式（见图21）。该设计方案中，以端齿危险点的齿形为基准，将端齿圆弧面简化为平面。该设计方案选择了试验件的压力角θDC、山形角λDC、齿根圆角RDC、齿高HDC、齿底宽WDC为关键尺寸，保证其与真实结构一致。在此基础上，在考核段的两端设置了凸台，目的是减小考核段的刚性，并调整危险点的应力分布。该设计方案中包括4个可调整的几何参数：半宽度BDC、凸台厚度TDC，凸台高度DDC和凸台圆角R′DC。

图21 端齿模拟件结构形式Fig.21 Configuration of simulating specimen for curvic coupling of turbine disc

开展模拟件的有限元分析，对比上述几何参数的敏感性（见图22，其中下标“0”为参数敏感性分析的参考值），选择对SWT参量分布影响最大的半宽度BDC作为优化变量开展优化，使模拟件的考核部位临界距离范围内的SWT参量与真实结构的一致。通过参数优化，端齿模拟件的最大主应变分布见图23，端齿模拟件与真实轮盘SWT参量的分布对比见图24。在临界距离范围内，最大误差不超过7.0%。

图22 端齿模拟件几何参数敏感性对比（BDC0=9 mm，TDC0=5 mm，DDC0=4 mm，RD′C0=4 mm）Fig.22 Comparison of geometrical parameter sensitivity of simulating specimen for turbine disc curvic coupling（BDC0=9 mm， TDC0=5 mm， DDC0=4 mm， R′DC0=4 mm）

图23 端齿模拟件最大主应变分布Fig.23 Maximum principal strain distribution of simulating specimen for turbine disc curvic coupling

图24 端齿模拟件与真实端齿部位SWT参量对比Fig.24 Comparison of SWT parameter distribution between hotspots of simulating specimen and turbine disc curvic coupling

随后，设计模拟件的夹持段与过渡段。夹持段采用销钉夹持的方案，宽度与厚度均大于考核段，2个方向上均采用圆弧过渡。端齿模拟件设计结果见图25。

图25 端齿模拟件设计结果Fig.25 Design result of simulating specimen for curvic coupling

最后，从真实涡轮盘毛坯的前轴颈部分周向取样并加工，其中端齿模拟件考核部位与涡轮盘端齿处的粗糙度一致。

开展端齿模拟件的低周疲劳试验，试验温度为550 ℃，加载频率为10 Hz，试验条件见表4。这里考虑到销钉夹具的加载能力，将载荷比R=0的情况调整为R=0.1。试验设备与试验流程与2.2节一致。试验结果见图26。

表4 端齿模拟件低周疲劳试验条件（550 ℃）Table 4 Conditions of fatigue experiment for curvic coupling simulating specimen at 550 ℃

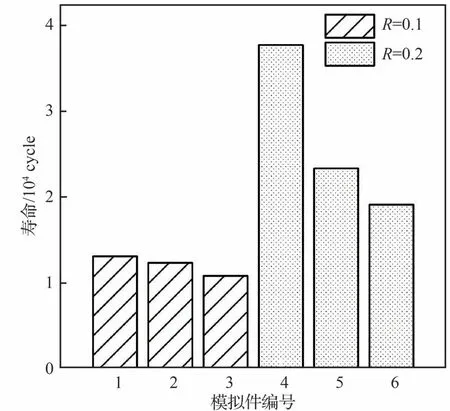
图26 端齿模拟件疲劳试验结果Fig.26 Results of fatigue experiment for curvic coupling simulating specimen

所有的端齿模拟件均从考核部位断裂（见图27），说明试验的有效性。由图28所示的SEM断口观测结果可见，端齿模拟件均从应力集中部位的表面起裂（箭头指示位置为裂纹源），裂纹源存在明显的类解理特征。由此推断裂纹萌生于表面的薄弱晶面。

图27 试验后的端齿模拟件照片Fig.27 Photo of curvic coupling simulating specimen after experiment

3 端齿模拟件的整盘试验验证

为验证模拟件的设计方法，开展了高压涡轮盘的旋转疲劳试验。通过调整转速、轮缘载荷、局部位置形状等措施，保证试验中轮盘考核部位的应力与服役状态时一致［33］。试验温度为200 ℃，试验转速为1 000 r/min-20 000 r/min-1 000 r/min的交变转速。试验结果显示，涡轮盘前鼓筒内圈的端齿根部在循环载荷作用下萌生了2处疲劳裂纹，利用断口反推技术确定平均裂纹萌生寿命为13 069次循环。模拟件试验在100%转速、R=0.1条件下对应的平均疲劳寿命为12 102次循环，对比涡轮盘旋转疲劳试验结果，相对误差为7%，证明了所设计的轮盘模拟件能够反映考核部位的疲劳寿命。

图29为断裂的端齿部位，其中箭头指示为裂纹源。图30为断口的扫描电子显微镜观测结果。根据图30所示，裂纹源位于端齿根部应力集中部位的表面，裂纹源附近存在类解理结构，由此推断在循环载荷下，裂纹萌生于应力集中部位表面的薄弱晶面。这与模拟件试验的结果是一致的，进一步验证了模拟件设计方法的有效性。

图29 断裂的涡轮盘端齿部位Fig.29 Fractured curvic coupling on turbine disc

图30 涡轮盘端齿断口形貌Fig.30 Fracture morphology of curvic coupling on turbine disc

4 模拟件设计方法的稳健性讨论

上述研究已经说明所建立的模拟件设计方法应用于轮盘疲劳寿命评估的有效性，但是该方法在应用过程中的稳健性仍需要被讨论。本研究分析了疲劳寿命模型、临界距离模型的参数存在微小扰动时对设计结果的影响。式（3）～式（5）中，当参数E、σ′f、b、ε′f、c、α、β均存在±1%扰动时，计算获得的临界距离将发生一定的偏差，记作L^。以上述的模拟件为例，图31对比了不同模拟件在材料参数存在±1%的偏差时(-L)/L的值，代表了临界距离对不同材料参数的敏感性。由图31所示结果可知，当材料参数发生了±1%的偏差时，临界距离最大将发生1.9%的偏差。

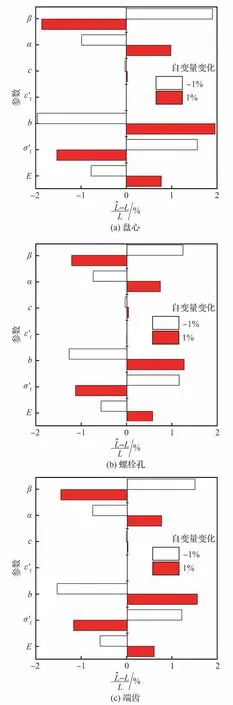
图31 材料参数扰动引起的临界距离偏差Fig.31 Critical distance deviation due to material parameter perturbation

但是计算临界距离的偏差并不一定会影响模拟件设计的结果。因为临界距离的计算结果L^高于实际值时，设计者会在更大范围内保证模拟件的SWT参量与真实构件一致。根据临界距离理论，这不会造成两者疲劳寿命的偏差。只有当L^低于实际值时，在L^≤x≤L的范围内，设计者设计的模拟件SWT参量的分布可能与真实结构产生偏差，影响疲劳寿命（如图32所示）。设这一区间内SWT参量的最大偏差为ΔPmax，对于常见的拉伸循环载荷下的模拟件，ΔPmax＜PSWT(L)，可以以此估计平均后的SWT参量Pm的偏差上限：

图32 低估临界距离引起模拟件SWT参量分布偏差示意图Fig.32 Underestimation of critical distance causing deviation of SWT parameter distribution of simulating specimen

式中：ΔPm为Pm的偏差；为含有偏差的平均SWT参量；P^SWT为含有偏差的SWT参量。这里忽略了模拟件SWT参量分布产生偏差后实际临界距离的变化，统一采用了真实结构的临界距离L计算平均SWT参量。

以上述的模拟件为例，图33分析了材料参数扰动引起的平均SWT参量Pm变化。相比临界距离的偏差，Pm的偏差普遍更小，均小于1.0%。这是由于在距离应力集中部位较远的区域应力应变普遍偏小，SWT参量产生的偏差有限，经由式（3）平均后对平均SWT参量Pm的影响将更小。这证明了所提出的方法具有一定的稳健性。

图33 材料参数扰动引起的平均SWT参量Pm偏差Fig.33 Average SWT parameter Pm deviation due to material parameter perturbation

同时，针对这种情况，在模拟件的设计过程中，设计者可以根据所使用的寿命模型、临界距离模型的预测精度，适当增加设计过程中保证SWT参量一致的范围，以避免低估临界距离而带来的偏差。

5 结 论

1） 以保证模拟件的基本几何形状、材料、临界距离范围内的SWT参量分布与真实轮盘一致为设计准则，提出了一种基于SWT参量一致的轮盘模拟件设计方法。

2） 实现了某型航空发动机高压涡轮盘盘心、螺栓孔、端齿等危险部位的模拟件设计，与真实涡轮盘相比，SWT参量的最大误差在7.0%以内。在此基础上，从真实涡轮盘毛坯相应位置处取样，开展了模拟件的低周疲劳试验，获得了不同载荷下模拟件的低周疲劳试验数据。

3） 开展了某型发动机真实高压涡轮盘旋转疲劳试验，并与模拟件疲劳试验结果对比，两者裂纹萌生寿命相对误差为7%；同时，疲劳断口对比表明，二者裂纹源均萌生于表面的薄弱晶面处。

本文提出的轮盘模拟件设计方法的有效性得到了证明。该方法主要针对低周疲劳失效模式，对于蠕变-疲劳、多轴疲劳等失效模式的适用性还需要进一步开展研究。