基于拟合误差消除的探地雷达图像鲁棒双曲线识别模型

兰 天 赵 毅 陈宏畅 龚俊波 王长军 王 健 杨小鹏

（1.北京理工大学信息与电子学院雷达技术研究所，北京 100081；2.北京理工大学重庆创新中心，重庆 401120；3.北京中建建筑科学研究院有限公司，北京 100070）

1 引言

作为探测地下未知物体的无损工具，探地雷达（ground penetrating radar，GPR）已广泛应用于各个领域［1］，如军事［2］、土木工程［3］、桥梁测量［4］、分层探测［5-6］等。脉冲探地雷达是一种常见的探地雷达系统，它向地下发射短电磁脉冲，并接收物体反射的信号，以探测地下区域。一般来说，探地雷达B-scan图像中生成的双曲线形特征［7］代表地下目标。然而，探地雷达B-scan 图像中的地下目标通常被杂波所掩盖，杂波主要由发射天线和接收天线之间的直接耦合、来自地面的反射以及来自地下不连续性的散射响应引起［8］。因此，从探地雷达B-scan 图像中自动提取双曲线具有挑战性。

由于霍夫变换技术［9］成功地用于变形形状拟合，因此它被用于在GPR B-scan 图像中提取双曲线，以定位埋藏物体［10］。此外，在［11］中，根据未知参数与实验误差的差异引入了加权因子，扩展了霍夫变换。此外，霍夫变换技术还用于揭示物体位置、深度、半径或速度［12］。由于基于霍夫变换的方法需要预先指定模型，计算量大，空间开销大，因此这些方法在实际应用中存在局限性。与霍夫变换不同，最小二乘法可以搜索和区分GPR B-scan 图像中的二次曲线［13-14］。然而，如果没有图像分割步骤，基于霍夫变换的大多数方法只能识别图像中的一条曲线。在文献［15-20］中，基于机器学习的方法被用来提取B 扫描图像中的双曲线等目标区域。其中，在文献［15］中，提出了一个由反向传播神经网络分类器、基于霍夫变换的模式识别方法、基于韦尔奇功率谱密度估计和边缘检测的图像特征处理方法组成的处理系统模型。在文献［16］中，Viola-Jones（VJ）算法被用来提取探地雷达数据中的目标区域。文献［17］中的方法在检测时，采用一种基于神经网络的方法对噪声信号进行分类。在文献［18］中，作者提出了包括数据过滤、检测和目标分类的双曲线自动检测和分类方法，在数据过滤部分利用了小波分析和Gabar 滤波器，在检测分类部分提出了基于层次分析的目标分类方法。在文献［19］中，作者提出了一种基于相位对称的手工特征，称为定向矢量相位对称直方图（histogram of oriented vector phase symmetry，HOVPS），该特征作为分类器的特征输入以实现对双曲线的检测。对于上述基于机器学习的方法，大多数特征需要专家来识别，并且训练数据并不足以满足所有不同的检测条件。此外，在文献［20］中提出了一种结合深度学习网络RetinaNet 的自动检测双曲线的方法，取得了0.58的平均精度。近年来，有一些研究实现了能够自动检测和拟合B-scan 图像中双曲线的集成模型［21-22］。在文献［21］所提出的模型中，首先对Bscan 图像进行预处理，将其转化为二值图像。然后提出了列连接聚类算法（column-connection clustering，C3）来分离有交集的双曲线。之后，采用基于神经网络的方法从C3 算法的输出中识别双曲线特征。虽然该模型包含了图像处理、机器学习等方法，但该模型的C3算法没有考虑双曲线垂直向下开口这一重要特征。为了解决这一问题，文献［22］提出了开放扫描聚类算法（open-scan-clustering algorithm，OSCA）。OSCA 通过从上到下扫描预处理后的二值图像中向下的开口来进行聚类。然后，基于抛物线拟合的判断（fitting-based judgment，PFJ）方法从OSCA 的输出中识别双曲线特征。然而OSCA中的下开口特征是B-scan 图像的像素级局部化特征。因此，OSCA 的输出包含一些具有下开口特征的非双曲点集。而且，PFJ 方法不能有效地消除这些非双曲点集。为了去除这些非双曲点簇，本文提出了一种鲁棒集成模型。该模型由预处理方法、OSCA、基于代数距离的双曲线拟合算法和基于拟合误差的消除（fitting-errors-based eliminating，FEE）方法组成。其中，FEE 方法根据非双曲点簇的拟合误差远大于双曲点簇的拟合误差的特点消除了OSCA 生成的开口向下的非双曲点簇，实现了GPR图像中所有双曲点簇的拟合和识别。

本文其余部分组织如下。预处理方法在第2节中介绍，然后在第3 节介绍OSCA，随后在第4 节介绍双曲线拟合算法，第5 节介绍FEE 方法，第6 节展示实验研究，最后在第7节得出结论。

2 预处理方法

在本节中，介绍了预处理过程，包括均值对消、自适应阈值算法和开闭运算。

2.1 均值对消

在应用所提出的阈值分割算法之前，采用每个扫描道数据减去所有扫描道数据的平均值的操作来抑制杂波和噪声。均值相减运算前后的图像如图1所示。图1（a）中的亮条被抑制，这表示发射和接收天线与地面反射的直接耦合。为了评估平均减法操作的有效性，利用信号杂波比（SCR）并定义为

图1 均值相减操作Fig.1 Effect of mean subtraction operation

其中，BM×N表示B扫描图像，TI×J表示B扫描图像中的目标区域。经过均值相减运算，SCR 得到改善，如表1所示。

表1 均值相减前后的SCRTab.1 SCR of images before and after mean subtraction operation

2.2 自适应阈值算法

由于探地雷达图像中垂直灰度值的变化代表了介质不连续面的反射，因此对垂直灰度值变化点的灰度值进行处理，计算阈值。梯度G(x，y)可由

其中V(x，y)是灰度值。由于均值对消运算后存在残余杂波和噪声，若将阈值计算为

阈值过低，实验结果就会变差。因此，本文算法中的阈值定义为

在（4）中，Ve(x，y)代表大于最大灰度值的一定百分比的像素点灰度值，Vy(x，y)代表在G(x，y) ≠0处的像素点灰度值集合，MaxVy(x，y)代表集合中的最大灰度值，ρ是一个分数（0 ＜ρ＜1）。为了分析ρ的影响，对所提出的阈值分割算法进行了不同ρ值的测试。如图2所示，ρ=0.5的阈值太低，只有一些非目标区域被去除；ρ=0.7的阈值太高，双曲特征变得不完整。因此，本文提出的阈值算法采用ρ=0.6。该阈值算法基于［22］中的自适应阈值法。为了比较性能，这两种方法在真实的B扫描图像上进行了评估，如图3所示。［22］中提出的方法得到的阈值过低，只能去除一些暗区。如表2所示，图3（c）的SCR高于图3（b），因此本文提出的阈值算法性能优于［22］中的阈值算法。

表2 不同阈值处理后的图像SCR值Tab.2 SCR of images processed by different thresholding methods

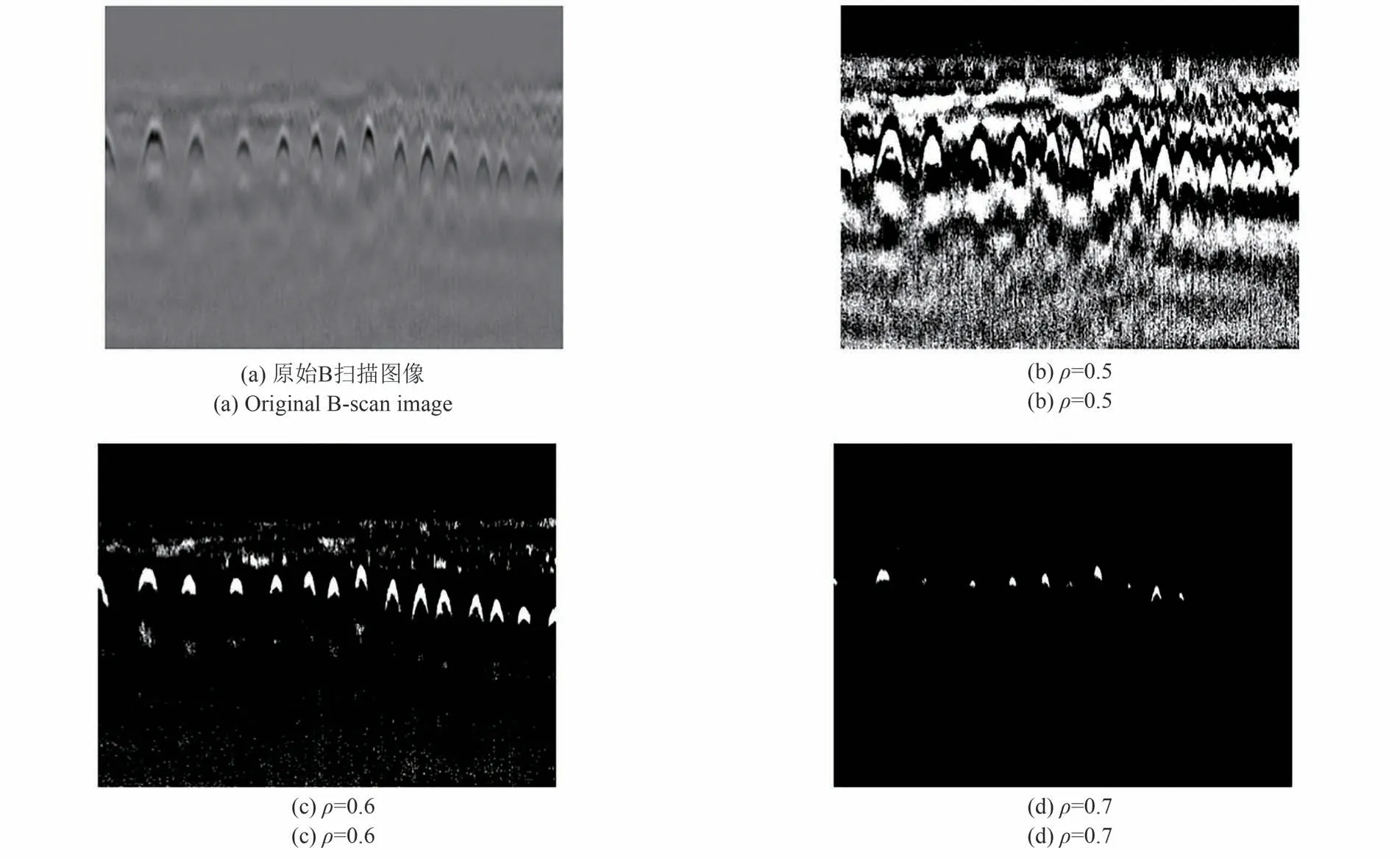
图2 所提出的方法不同ρ值下阈值处理后的图像Fig.2 Thresholded image by the proposed method with different values of ρ

图3 不同阈值方法处理后的图像Fig.3 Thresholded image of different methods

2.3 开闭运算

打开和关闭操作是两个形态操作［23］。这两种操作都是两种基本形态操作的组合：扩张操作和侵蚀操作。膨胀操作用于连接相似特征的区域，侵蚀操作用于去除明亮的噪声点。二值图像I通过结构元素SE的打开操作定义为：

这表明I受到SE1 的侵蚀，接着是SE2 的膨胀。同理，通过SE对I的关闭操作定义为：

这表明了SE1 对I的膨胀以及SE2 对结果的侵蚀。

在所提出的处理方法中，首先应用闭操作来融合窄裂缝和细长裂缝，消除小孔，填充轮廓中的空隙。然后使用开操作来平滑物体的轮廓，打破狭窄的峡部，消除小的突出。为了最大限度地保留图像，在闭操作中使用半径为3的圆形结构元素，在开操作中使用半径为2的元素。开闭操作后的处理结果如图4（c）所示。

图4 所提出的预处理方法后的图像Fig.4 Images after the proposed preprocessing method

3 开口扫描聚类算法

经过OSCA 处理后的B 扫描图像，可以去除大部分非双曲线点簇。OSCA 基于一些概念，包括“点段”、“下/上开口”和“点段参数存储阵列”。“点段”指的是连续的两个以上的点。一个点段与另两个不连接的点段水平重叠，它们之间在下一行中有间隙，上面的点段定义为开始向下的开口。同样，向上开口也可以定义为位于连续两行的三个连通点段，其中一个点段与前一行的另外两个不连通点段水平重叠，且它们之间有间隙，较低的点段定义为开始一个向上开口。“点段”和“下/上”开口如图5 所示。“点段参数存储数组”是存储点段参数的数组，在（7）中定义，（7）中的符号在表3中解释。

表3 公式（7）中符号的含义Tab.3 Meaning of symbols in Eq.（7）

图5 开口像素表示Fig.5 Pixel representation of opening

通过生成该阵列，OSCA 的操作思路可以从二值图像转移到“点段参数存储阵列”。根据上述定义，通过扫描每一行中的点段和相邻行中的点段，可以找到向下/向上的开口。在第一次扫描中，该算法的目标是找到向上的开口。找到向上开口后，标记向上开口的点段，并连续标记其下方的相邻点段。当标记出向上开口的底部点段时，算法会检查该点段是否开始向下开口。如果出现这种情况，则会出现x 形相交的情况，在第二次扫描时对这种情况进行操作。否则，这个向上开放簇的所有点段将被删除。在第二次扫描中，当发现向下的开口［见图6（a）］时，算法将检查该点段是否开始向上的开口。如果没有，则在点段参数存储阵列中记录开放范围[S，E]，见图6（b），并构建新的点集。向下开口点簇的顶部区域可以向上寻找小于或等于下面开口点簇的点段，直到没有点段满足这一要求［见图6（c）］。通过扫描左右两侧向下开口下方重叠的点段可以得到尾部［见图6（c）］。顶部和尾部的所有点将被添加到构造的开放点集群中。如果发生这种情况，X 形交叉上的处理见文献［22］。OSCA 算法的伪代码见算法1。通过使用OSCA，大多数没有下开口的非双曲点集在B扫描图像中被消除。

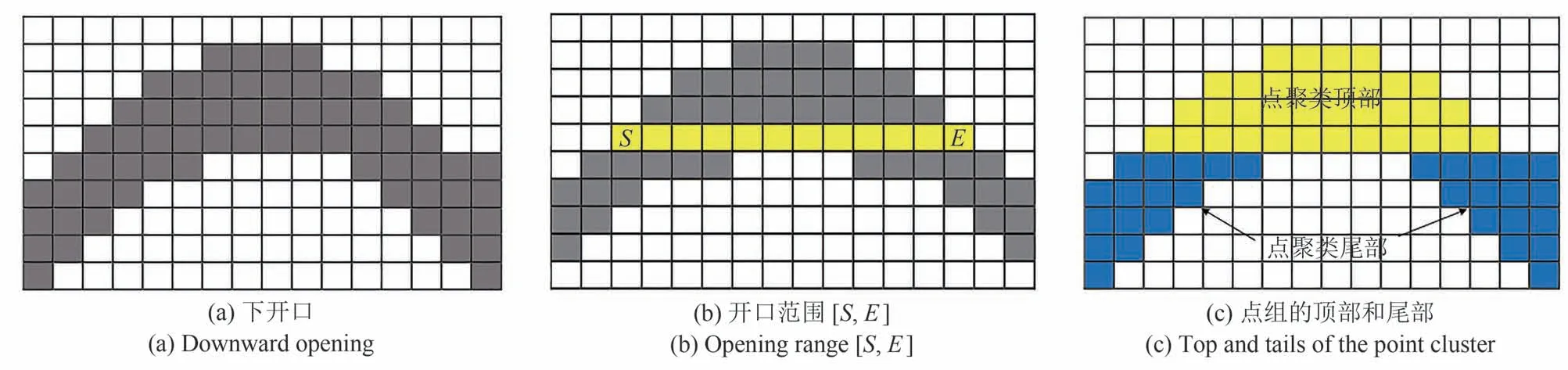
图6 OSCA中概念的像素表示Fig.6 Pixel representation of concepts in OSCA

公式（7）中各参数的含义如表3所示：

4 基于代数距离的双曲线拟合算法

在双曲线拟合算法之前，介绍了一种拟合点提取方法。通过在每个向下开放点簇的每列中自动提取一组均位点，得到拟合点集。首先，逐列扫描每个向下开口点簇，找到每列的上端点PU=(x0，y1)和下端点PL=(x0，y2)；然后得到各列的拟合点PF=(x0，(y1+y2)/2)。如图7所示，拟合点用黄色标记。

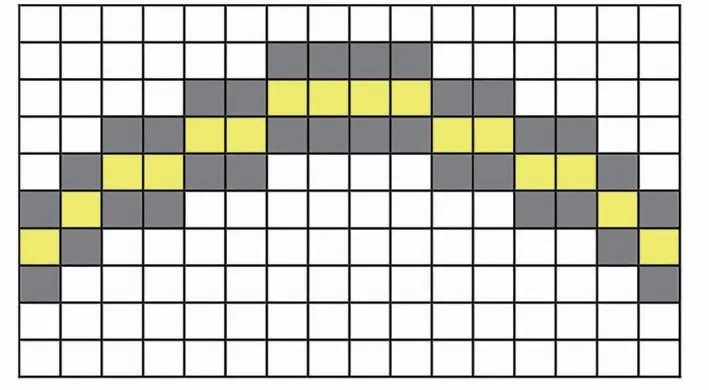
图7 拟合点（黄色标记）Fig.7 Fitting points（tag yellow）

拟合点集定义为PF={(xi，yi)∣1 ≤i≤n}，拟合问题建模为约束最小二乘问题。在本文拟合算法中，双曲线方程可以表示为

该双曲线标准方程可以转化为一般方程

式（9）可以简单地表示为

从一点到曲线的代数距离定义为

曲线到点簇的代数距离的平方和为

由于所有拟合点都需要在拟合双曲线的中心(x0，y0)以下，且拟合双曲线的中值需要位于双曲线点簇的开放范围[S，E]内，因此需要增加两个约束条件，表示为

根据式（10）、式（12）、式（14）、式（15），可以将双曲线拟合算法表示为凸优化问题：

其中≤表示两个向量之间的元素小于或等于

该凸优化问题也是一个约束线性最小二乘问题，可以用内点凸四元规划算法［24］来求解。利用该拟合算法，可以初步拟合OSCA得到的下开口点集。

5 基于拟合误差的剔除方法

采用双曲线拟合算法对所有下开口点集进行拟合后，拟合点簇(1 ≤i≤N)（N＞2）的拟合误差定义为

其中Di为第i个拟合点簇的式（13）矩阵，xi为第i个双曲线拟合问题的解。OSCA 的输出点集可以分为非双曲点集和双曲点集。为了区分这两类点簇，定义了非双曲点簇的判断标准为

如图8 所示，由于非双曲点集不具有完全的双曲线特征，非双曲点集的拟合误差会比双曲点集的拟合误差大得多，应用这种消去方法可以消去大多数非双曲点集。

图8 三个非双曲点集的像素表示Fig.8 Pixel representation of three non-hyperbolic point clusters

6 合成数据和实测数据实验结果

在本节中，展示和分析了在合成数据集和实测数据集上的实验结果。本节最后对本文提出的非双曲线点集消除方法与［22］中提出的PFJ方法进行了比较研究。

6.1 合成数据实验

利用电磁模拟器gprMax［25］生成模拟探地雷达B扫描图像。该开源软件允许用户通过设置不同的相对介电常数和电导率来指定不同的介质，并在不同的场景中设置不同的参数来指定不同的埋藏目标的大小。基于单层钢筋网格场景，采用gprMax 软件生成综合数据。如图9所示，6根钢筋埋在gprMax定义的土壤介质中。发射天线和接收天线靠近分界面，并以步长Δx=0.8 m的方式从x=0.2 m移动到x=1.8 m。

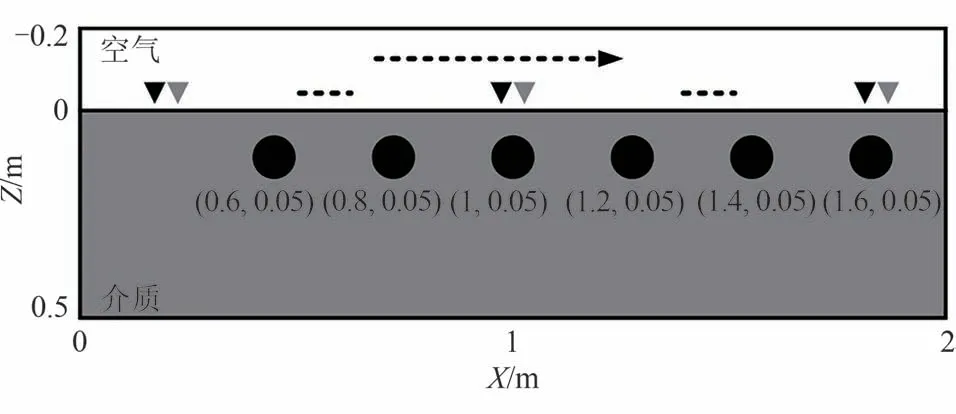
图9 仿真单层钢筋网格场景的剖视图Fig.9 Sectional view of the synthetic single layer rebar mesh scene

图10（a）和图10（b）分别为均值对消后的原始B 扫描图像和预处理后的图像。OSCA 和双曲线拟合算法的结果如图10（c）和12（d）所示。由于介质的异质性，图10（a）原始B 扫描图像中存在一些杂波。在没有其他物理干扰的情况下，图10（c）的OSCA 结果中没有出现非双曲点簇。在本次合成数据实验中，本文提出的B 扫描处理模型自动拟合并检测出所有正确的双曲点集。合成数据集实验的具体结果如表4所示。

表4 合成数据实验结果Tab.4 Obtained results on synthetic data sets

图10 所提方法处理仿真数据结果Fig.10 Images of the synthetic data processed by the proposed model

6.2 实测数据实验

数据集采集由具有1500 MHz 天线的LTD-2600探地雷达设备进行，用于检测图11中修复水泥路面下的钢筋网。钢筋网由半径6 mm，相邻距离40 cm的钢筋组成，埋在地表下10 cm处。

图11 GPR设备和数据收集Fig.11 GPR equipment and data collection

如图12 所示，（a）和（f）分别为数据1 和数据2经过均值对消之后的图像结果。通过预处理方法，将B 扫描图像转化为包含下开口点集和一些不规则区域的二值图像，如图12（b）和（g）所示。然后通过OSCA 去除不规则区域，识别出所有下开口点集，但保留了一些具有下开口特征的非双曲点集，如图12（c）和（h）所示。随后利用FEAA 对OSCA 结果进行处理，剔除了非双曲线点集，保留了所有目标双曲点集，如图12（d）和（i）所示。最后进行双曲线拟合得到结果，如图12（e）和（j）所示。在实测数据集上得到的结果如表5 所示。图13 为在进行FEAA方法处理时，各拟合点集的误差与所有点集误差均值的2 倍比较结果。在图13（a）中，展示了图12（c）中（数据1）中9 个点集的拟合误差，从图中可以看出，第一个点集的误差大于误差均值的2 倍，因此相比于图12（c），在图12（d）中消除了第一个非双曲点集。在同样的情况下，在图13（b）中，展示了图12（h）中（数据2）中6 个点集的拟合误差，从图中可以看出，第一和第二点集的误差大于误差均值的2 倍，因此相比于图12（h），在图12（i）中剔除了这两个非双曲点集。

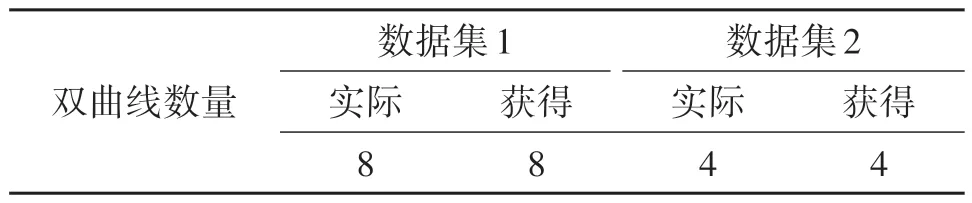
表5 实测数据集实验结果Tab.5 Obtained results on real datasets

图12 由所提方法处理实测数据集结果Fig.12 Images of real datasets processed by proposed model

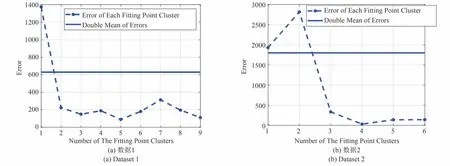
图13 各拟合点集误差与所有点集误差均值的2倍比较结果Fig.13 Comparison between the error of each fitting point cluster and double mean of errors of all point cluster

为了进一步验证FEE 方法的有效性，进行了PFJ 与FEE 方法的对比实验。图14（a）为进行抛物线拟合的结果，且式（21）为数据集1 中非双曲点集的拟合抛物线方程。根据PFJ 方法，该非双曲点集无法消除，如图14（b）所示。而这种非双曲点集可以通过FEE 方法消除，如图12（c）和12（d）所示。FEE方法和PFJ得到的双曲线点集数如表6所示。

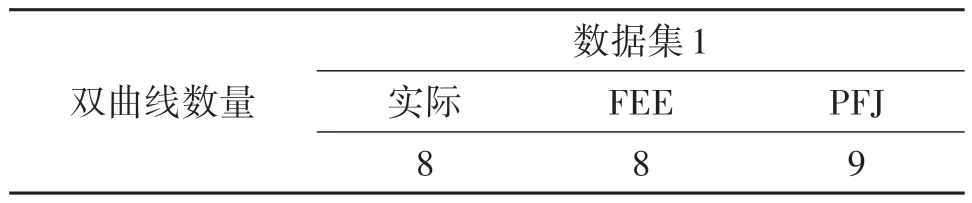
表6 FEE和PFJ方法得到的双曲线点集数Tab.6 Number of obtained hyperbolic clusters of FEE and PFJ

图14 PFJ处理数据集1结果Fig.14 Images of dataset 1 processed by PFJ

y=-0.0027x2+0.1820x+710.3430 （21）

7 结论

本文提出了一种基于非双曲点集消除方法的鲁棒集成模型：基于拟合误差的消除（FEE）方法，用于自动识别和拟合探地雷达（GPR）B 扫描图像中的双曲线。在我们的模型中，首先对B 扫描图像进行阈值分割开闭操作处理，然后采用OSCA 方法对下开口点集进行分离，随后采用基于代数距离的双曲线拟合算法。最后，利用FEE 方法可以对所有的双曲点集进行检测和拟合。综合仿真和实测数据实验结果，验证了所提模型的有效性和鲁棒性。对于所提出的方法，待改进部分为双曲线识别部分，可以结合深度学习领域的识别方法以提高方法的鲁棒性。此外，可以采用先利用深度学习方法进行检测，后进行拟合的方法思路。