任意构型双基SAR运动目标图像特征分析

杨 果 王雨晗 王佳慧 邓钱钰 毛新华

（南京航空航天大学电子信息工程学院雷达成像与微波光子技术教育部重点实验室，江苏南京 211106）

1 引言

合成孔径雷达（Synthetic Aperture Radar，SAR）具有高分辨、大幅宽、全天时全天候工作［1］等优势，因此无论是在军事领域还是在民用领域都得到了广泛的应用。SAR的两种经典结构分别为单基SAR和双基SAR［1］。其中，单基SAR收发共用一部天线，具有相对简单的成像系统和成像处理过程。相对而言，双基SAR 的发射机和接收机安装在不同的平台上，正是这种结构使双基SAR 拥有单基SAR 没有的优势，例如更高的系统设计灵活性、更多的目标散射信息，配置灵活、作用距离远、隐蔽性好、抗干扰能力强等［2-3］。因此，双基SAR越来越被重视。

研究者对于双基SAR 静止目标成像已经有了较为深入的研究［4-5］，提出了一系列的算法和对应的改进算法，技术水平已经相对成熟。而对于运动目标的研究虽然也已经取得了一些成就［6-8］，但仍然面临着许多重大挑战，尤其是在双基结构下的研究方面［9-10］，许多问题有待突破。首先，相比于单基的单双曲线而言，双基SAR 静止目标的距离历程函数是双双曲线［11］，回波信号的表达式已经非常复杂，更不用说运动目标。这给运动目标的频谱分析带来了困难。其次，通常情况下目标是非合作的，其运动的方向和速度都是未知的，这将给目标带来额外的成像位置偏移和成像结果散焦。因此，目标位置的校正和图像的重聚焦是动目标成像的两个关键问题。

在进行目标位置校正和图像重聚焦之前，首先要研究清楚运动目标的回波信号的相位特性，分析清楚目标的运动对成像结果的影响。SAR成像算法一般可以分为两类，一类是时域算法，另一类是频域算法。由于时域算法的效率较低，因此在工程上很少使用，本文主要考虑频域算法。本文从匹配滤波后的回波信号开始进行成像处理，此时，频域算法的成像处理过程可以大致分为两步，首先是去除距离和方位的耦合项和高阶项，然后进行两维傅里叶变换即可实现成像。现有的文献［12-14］对相位误差的分析都是在相位历史域进行的，然后根据分析的结果预测图像域中的目标特征。然而，图像域与相位历史域之间的关系其实并不明确，对于不同的成像算法而言，去除耦合项和高阶项的方法不尽相同，例如Omega-K 算法使用的是stolt插值方法，PFA算法使用的是一个两维插值，其中包含keystone变换操作。而在此过程中有可能引入新的相位误差，从而对成像结果造成影响。因此，通过相位历史域中分析的相位误差特性，并不能十分准确的预测运动目标在图像域中的成像结果。但是，波数域和图像域满足简单的傅里叶变换关系。因此，只要分析清楚了波数域中的相位误差特性，根据已知的傅里叶变换的性质，就能直接准确地预测目标的运动对目标成像结果的影响。

本文首先介绍了静止和运动目标的双基SAR成像原理，建立了成像几何，从而得到了信号模型。基于上述运动目标的信号模型，对回波信号进行PFA 成像算法处理，然后对比分析了成像处理前后的相位误差特性。一方面，揭示了波数域中的两维相位误差导致图像中的目标发生两维位置偏移和两维散焦的现象。并且上述两维位置偏移和两维散焦的方向沿着同一条倾斜的直线。也就是说，无论运动目标的速度矢量指向何方，图像域中的目标都将沿着同一条直线发生偏移。另一方面，通过一个合适的坐标旋转，能使PFA 图像中目标的位置偏移和散焦的维度从两维降到一维，从而能够降低后续的目标重定位与图像重聚焦的难度和复杂度。最后，通过仿真实验对上述结果进行了验证。

2 成像几何和信号模型

图1 为双基SAR 数据收集几何模型，成像场景中心定义为坐标原点，地平面定义为x-y平面。不失一般性，假设发射机和接收机的几何构型任意，即它们分别在Ht和Hr高度沿着各自的方向飞行，速度为vt和vr。本文中t表示慢时间（方位时间），t=0定义在孔径中心。发射机和接收机到场景中心的瞬时距离分别表示为Rt=Rt(t)和Rr=Rr(t)。所对应的瞬时俯仰角和方位角分别表示为θT=θT(t)，φT=φT(t)，θR=θR(t)和φR=φR(t)。它们对应的场景中心的值分别为θT0，φT0，θR0和φR0。假设位于场景内的任意运动目标的初始位置为(xm，ym)，运动速度为vm=(vx，vy)，其中vx，vy分别表示x，y方向的速度分量。运动目标到发射机和接收机的瞬时距离分别定义为RtM=RtM(t)和RrM=RrM(t)。

假设雷达发射脉冲信号，通过成像几何模型可知，目标静止时回波信号的瞬时距离历程可以表示为：

其中，(Xt0，Yt0，Zt0)和(Xr0，Yr0，Zr0)分别是发射机和接收机的初始位置，θvt和θvr分别是发射机和接收机的速度矢量方向。

经过匹配滤波［15］和运动补偿，双基SAR 静止目标的回波信号可以表示为［16］：

其中，c表示光速，fc表示发射载频，fτ表示距离频率，A表示回波信号的幅度，RΔ(t)表示双基静止目标差分距离。

同样的方法可以得到目标运动时回波信号的瞬时距离历程：

经过匹配滤波和运动补偿，双基SAR 运动目标的回波信号可以表示为：

其中，ε(t)表示目标运动引入的距离误差。

假设发射机和接收机远离成像场景，满足远场条件，即满足平面波假设。在这种情况下，式（2）中的双基静止目标差分距离可以近似为［17］：

于是，将式（5）代入式（4）可得：

3 相位误差结构

为了验证相对于传统方法的相位历史域，在波数域中预测目标在图像域中的成像结果更准确的结论，本节分别给出了相位历史域和波数域中的相位误差结构。其中，相位历史域中的相位误差信号可以根据上一节的信号模型直接得到，而波数域中的相位误差信号需要通过相位历史域中的相位误差信号变换得到。将信号从相位历史域转换到波数域的算法有很多，本文使用的方法是对相位误差域中的信号进行PFA 格式转化，从而得到波数域中的相位误差信号。

3.1 相位历史域中的相位误差

通过式（2）和式（4）可知，相位历史域（(fτ，t)域）中的相位误差可以表示为：

其中，2πfc·ε(t)/c表示方位向相位误差（Azimuth Phase Error，APE），ε(t)表示距离徙动（Range Cell Migration，RCM）。相位误差函数关于距离频率只有常数项和一次项，这意味着在匹配滤波之后，关于距离的二次项被去除，距离向压缩良好，不存在距离向散焦。另外，不难发现此时的APE和RCM满足相对简单的线性关系，这意味着两者只需要求得其一，就可以通过它们之间的线性关系求得另外一个。

3.2 波数域中的相位误差

要得到波数域中的相位误差，需要对相位历史域中的信号进行两维重采样转化成极坐标格式，为了提高计算效率，该两维重采样过程被分解为两个一维插值，从而实现从(fτ，t)域到(kx，ky)域的转化。对式（6）进行PFA格式转化可以得到

从式（8）不难发现，信号中除了想要的变量kx，ky，还存在多余的变量t。接下来需要将式（8）中的变量t去除，从而将信号完全转换到波数域。根据θT，θR，φT和φR的定义和图1所示的几何关系，易知θT，θR，φT和φR都是关于t的变量。通过式（9）不难发现kx/ky也是关于t的变量。也就是说，t可以表示成关于kx/ky的函数，假设它由下式给出

因为双基SAR 模型太复杂，所以式（11）很难表示成显式形式。

将式（11）代入到式（8），并且定义

于是，式（8）可以重写为

空间频率kx，ky可以表示成极坐标格式：

其中，kr表示斜距频率，θb表示双基角。

由上述分析可知，匹配滤波后的回波信号通过式（9）和式（11）可以从相位历史域转换到PFA 波数域（(kx，ky)域），同时两维相位误差也被转换到PFA波数域。根据式（13），PFA 波数域中的两维相位误差可以表示为：

4 相位误差特性分析和对目标成像结果的影响

SAR 成像算法的一般流程如图2 所示。其中，从相位历史域到波数域的过程，每个算法的实现方式都不尽相同，因此在这个过程中是否会引入新的相位误差并不确定。这就导致在相位历史域对成像结果进行预测存在一定的误差。然而，波数域和图像域之间的关系为简单的傅里叶变换关系，所以可以通过分析上一节得到的波数域中的相位误差结构，得到相位误差特性，然后再根据已知的傅里叶变换性质，直接对目标在图像域中的成像结果进行预测。相对于相位历史域中的预测结果，该预测结果将更准确、更可靠。

图2 SAR成像的流程图Fig.2 Flowchart of SAR imaging

为了更好地分析波数域中相位误差的特性，本文在kx=kxc，ky=kyc处对式（15）中的相位误差进行二阶泰勒展开，可以得到下式

其中，

值得注意的是，式（17）中g(kxc/kyc)=0。这是因为，当kx/ky=kxc/kyc时，发射机和接收机位于合成孔径中心，此时相位误差为零，即式（15）中的ψ(kxc，kyc)=kyc·g(kxc/kyc)等于0。由于kyc≠0，所以g(kxc/kyc)=0。

从前面的分析可知，波数域和图像域中的信号满足傅里叶变换关系。因此，根据傅里叶变换的性质可知，波数的线性项对应于目标在SAR 图像中的位置偏移，波数的二次项对应于SAR 图像上目标的散焦，耦合项则对应于SAR图像上目标的两维散焦。在式（16）中，a0和a1分别对应方位波数和距离波数的一次项，将分别导致方位向和距离向的位置偏移。a3表示耦合项，将造成两维散焦。a2和a4是方位向和距离向的高阶项，它们将会分别带来方位向和距离向的散焦。一般情况下，以上五个参数都不为零，因此，目标在图像中会发生两维偏移和两维散焦。

对比式（7）和式（16）不难发现，式（16）中存在距离波数的二次项，这说明回波信号从相位历史域变换到波数域时引入了新的相位误差，发生了二次散焦。这说明在相位历史域中预测图像域中的目标成像结果是不完全准确的。

将式（17）代入到式（16）可得

根据式（14）可以得到以下公式

其中，θb0表示中心时刻的双基角。于是，式（19）又可以重写为

式（21）的组成部分(cosθb0kx-sinθb0ky)恰好构成坐标旋转的形式。理论上，输出的PFA 图像的坐标系可以任意选取，通过选择合适的旋转角，对式（21）进行坐标旋转，式（21）可以表示为如下形式

旋转后的地平面坐标系定义为x′-y′，上述合适的旋转角恰好是双基角的中间时刻值θb0。

由式（22）可知，通过合适的坐标变换，前面分析的两维位置偏移和两维散焦可以降为一维位置偏移和一维散焦，同时还能把耦合项消除。这意味着在保证图像质量的同时，可以把后面的位置重定位和图像重聚焦处理的难度和复杂度降低。另外，目标的位置偏移和散焦的方向都是旋转后的方位向x′。图3 示意了目标的位置偏移和散焦的一般情况，将x-y坐标系的坐标原点从场景中心移动到目标的真实位置，得到新的坐标系xˉ-yˉ。

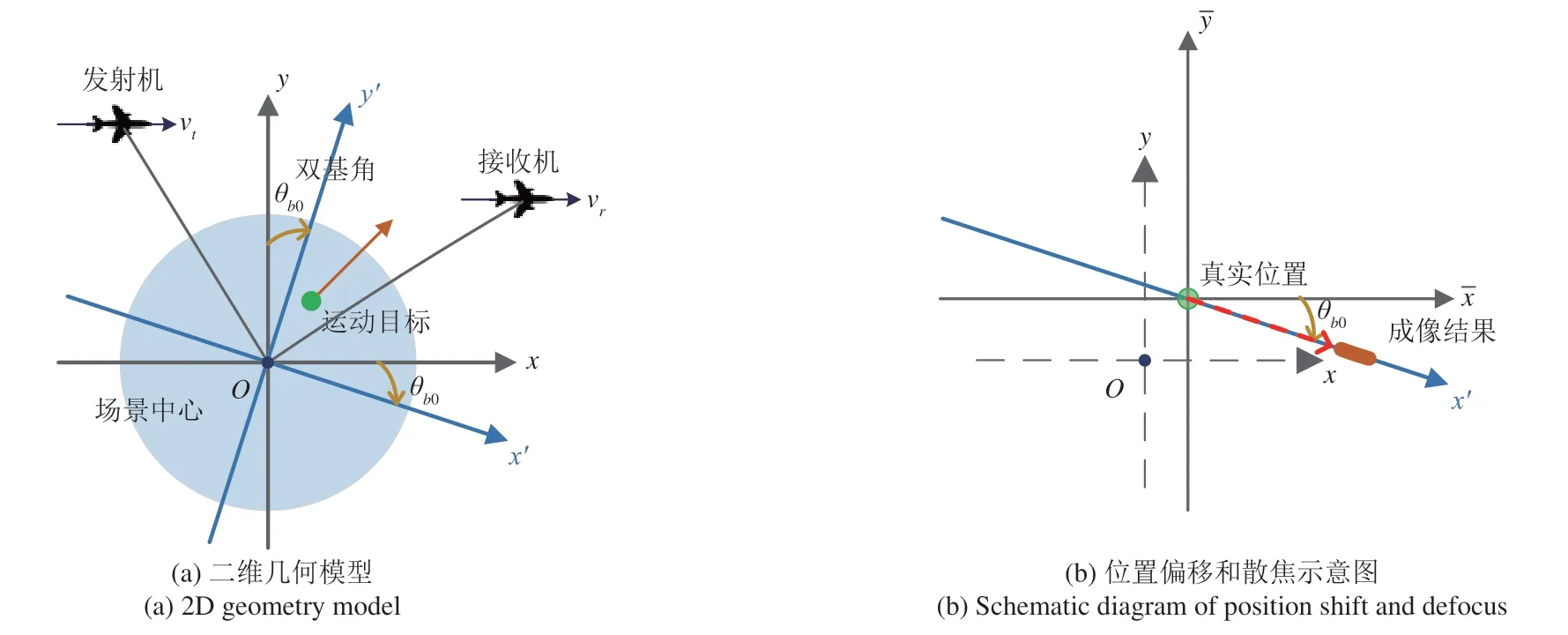
图3 运动目标在PFA图像中发生位置偏移和散焦示意图Fig.3 Schematic diagram of position shift and defocus of the moving target in PFA imagery

5 仿真实验

为了验证双基SAR 结构下运动目标的两维相位误差特性，本节进行了计算机仿真实验。实验的主要雷达参数如表1 所示，其中T 代表发射机，R 代表接收机。

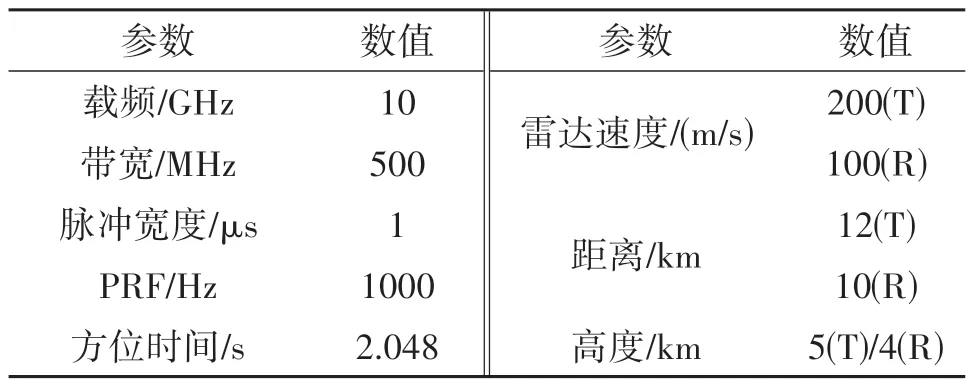
表1 仿真实验的主要参数Tab.1 Main parameters for the simulation

在本实验中，进行了点目标仿真，以验证双基SAR 运动目标回波信号经过PFA 算法处理后的残留两维相位误差对成像结果的影响。

仿真实验中的点目标的初始位置设置为（0，0）。坐标旋转前点目标的成像结果如图4所示。图4（a）是目标静止时的成像结果，可以很清晰地看出目标聚集良好，没有发生位置偏移和散焦。图4（b）是目标运动时的成像结果，从图中也可以很清晰地看出运动目标的成像位置和真实位置不一致，并且成像结果发生严重散焦。另外，从图中还可以看出此时的位置偏移和散焦都是两维的，方向都沿着旋转后的方位向x′。

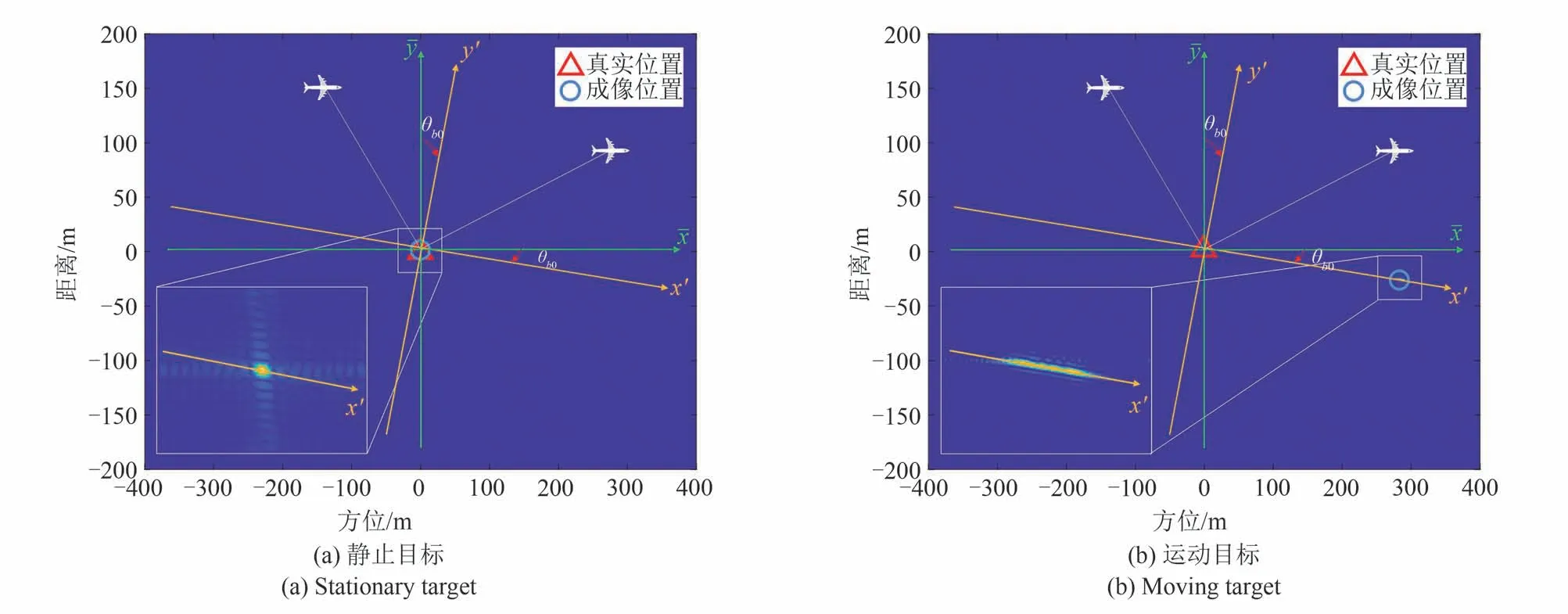
图4 图像域中的成像结果Fig.4 Imaging result in image domain

接下来进行坐标旋转后的仿真实验，仿真实验的点目标的初始位置同样设置为（0，0）。坐标旋转后的静止目标PFA 图像如图5（a）所示，而坐标旋转后的运动目标PFA图像如图5（b）所示。从图中可以看出运动目标的成像位置不在真实位置处，即目标发生了位置偏移，并且成像结果的散焦很严重。但是，幸运的是此时的位置偏移和散焦都是一维的。对比图4（b）和图5（b），可以说明通过合适的坐标旋转，运动目标的位置偏移和散焦的维度可以从两维降到一维，此实验现象和本文分析预测的结论一致。为了进一步验证上述结论，进行了点目标在不同速度下的仿真实验。仿真实验设置的速度矢量如表2所示，速度矢量的参考坐标系为x′-y′。为了更加清晰地显示不同速度下目标地成像位置，从而说明目标位置偏移的方向，将不同速度下的四个成像结果用一幅PFA图像展示了四种，结果如图6所示。图6（a）和图6（b）分别是坐标旋转前后的结果。从图6 可以很清楚的看出，坐标旋转前，目标的成像位置落在一条倾斜的直线上，即目标的位置偏移是两维的。坐标旋转后，点目标在PFA 图像中都沿着旋转后的方位向x′发生位置偏移和散焦，尽管点目标的实际速度方向各不相同。这也意味着从PFA 图像中不能直接看出运动目标的实际运动方向。目标在四种不同速度下的位置偏移由表3 给出。从表3 不难发现，坐标旋转前，目标在xˉ和yˉ方向都存在位置偏移。而坐标旋转后，目标只在x′方向存在位置偏移，y′方向的位置频移为零（近似）。

表2 仿真实验中设置的速度Tab.2 The speeds in the simulation experiment

表3 不同速度下的位置偏移Tab.3 Position shift at different speeds

图5 运动目标坐标旋转后的PFA图像Fig.5 PFA imagery of moving target after coordinate rotation

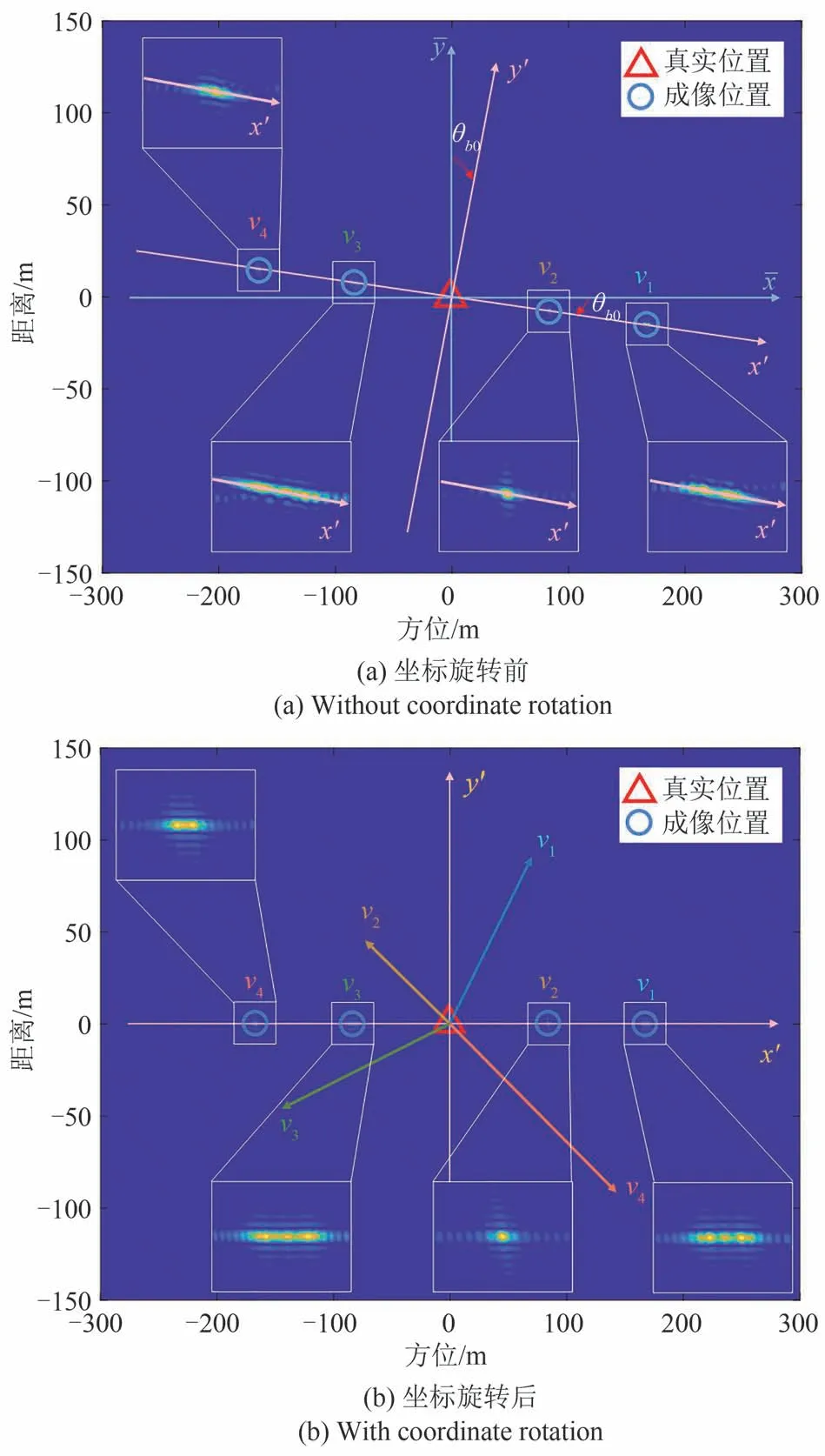
图6 不同速度下的PFA图像Fig.6 PFA imagery at different speeds

最后，用点目标构造了一个复杂的场景进行仿真实验。仿真实验中构造的复杂场景为舰船目标，该舰船目标如图7 所示。仿真实验中，针对坐标旋转前后两种情况，都设置了两组不同的速度，舰船目标的速度分别设置为（2，2）m/s 和（-2，-2）m/s。仿真实验的结果如图8 所示，前三幅图是坐标旋转前的结果，后三幅图是坐标旋转后的结果。从图8可以很清楚地看出，坐标旋转前，舰船目标的位置偏移和散焦都是两维的。而坐标旋转后，舰船目标的位置偏移和散焦的维度由两维降为一维。同时，由于进行了坐标旋转，输出的舰船图像是倾斜的，并且倾斜角等于旋转角。

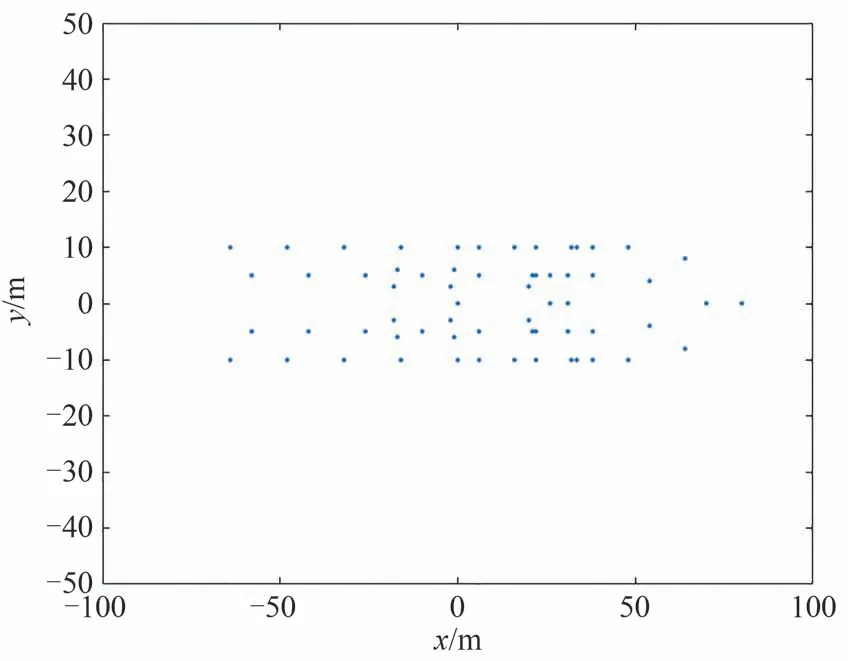
图7 舰船目标示意图Fig.7 Schematic diagram of ship target

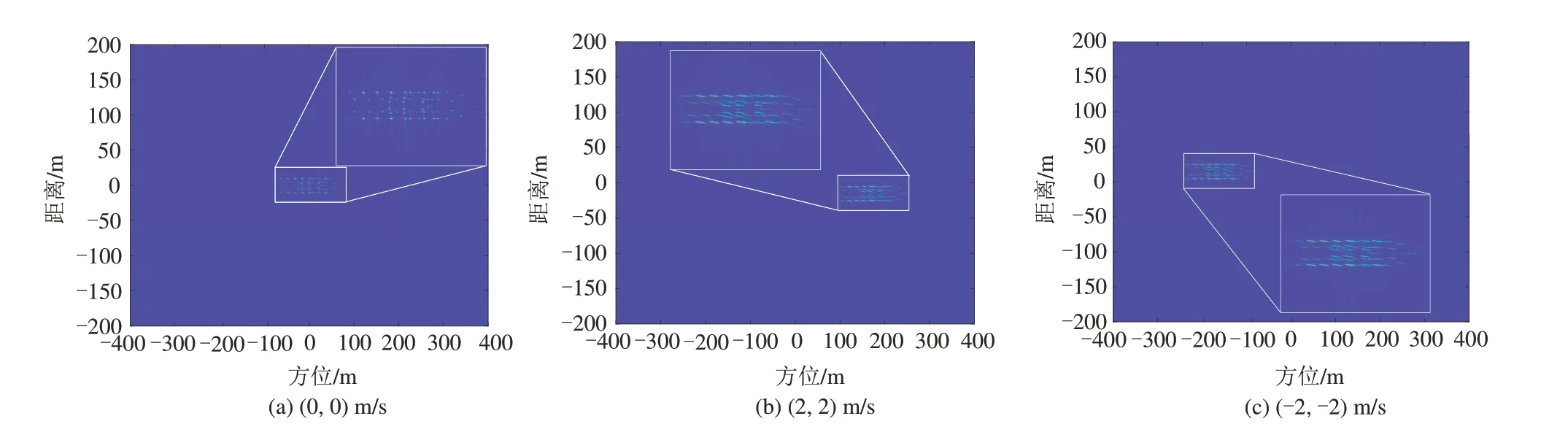
图8 坐标旋转前后舰船目标在不同速度下的成像结果.（a）～（c）为坐标旋转前的结果，（d）～（f）为坐标旋转后的结果Fig.8 The imaging results of ship target at different speeds before and after coordinate rotation.（a）～（c）is the result before coordinate rotation，and（d）～（f）is the result after coordinate rotation

6 结论

本文首先给出了双基SAR运动目标成像几何和信号模型，然后根据信号模型，对比分析了任意构型双基SAR运动目标回波信号在PFA算法处理前后的两维相位误差特性。通过分析相位历史域和波数域的两维相位误差特性的差异，解释了不同于传统方法的相位历史域，本文在波数域分析相位误差特性的原因。根据相位误差特性本文得出了以下结论，第一是目标运动引入的两维相位误差会导致目标发生两维位置偏移和散焦，这一点和传统方法的结论一致。另外，上述两维位置偏移和两维散焦的方向都沿着旋转后的方位向，这意味着无论运动目标的速度矢量指向何方，图像域中的目标都将沿着旋转后的方位向发生位置偏移和散焦，也就是说通过成像结果不能直接判断出运动目标的运动大小和运动方向。第二是通过合适的坐标旋转，目标的相位误差维度可以从两维降到一维，这意味着可以在保证图像质量的同时降低目标重定位与图像重聚焦的难度和复杂度。最后，仿真实验证明了上述结论的正确性。