基于最小极化RCS的昆虫雷达目标体型参数反演

王江涛 王 锐 李卫东 李沐阳 李云龙 钱李昌 胡 程

（1.北京理工大学信息与电子学院雷达技术研究所，北京 100081；2.北京理工大学前沿技术研究院，山东济南 250300；3.卫星导航电子信息技术教育部重点实验室（北京理工大学），北京 100081；4.中国人民解放军31511部队，北京 100037）

1 引言

大量昆虫在白天和夜间飞到高空进行数百公里迁飞［1］。作为生态系统重要组成部分，迁飞昆虫通过长距离迁徙实现物质和能量转移的同时造就了病虫害和疾病的传播［2］。根据中华人民共和国农业农村部统计，2017 年全国农业病虫害发生面积3.15 亿公顷，造成粮食损失119.54 亿公斤［3］。2023 年，农业农村部修订的《一类农作物病虫害名录》中，一类害虫有10种（类），其中迁飞害虫占比达80%。可见当迁飞昆虫是害虫时会直接对农业造成重大损失。如果能实现对迁飞害虫的实时监测，第一时间掌握害虫迁飞动向，建立预警机制，便可能从源头对迁飞害虫进行防治，防止大规模灾害形成和扩散。

雷达是无线电探测与测距的缩写，其基本原理是发射电磁波到感兴趣区域后接收目标散射回波。20 世纪60 年代早期，雷达被发现适用于监测昆虫迁飞，此后陆续出现多代昆虫雷达［4］。经过数十年发展，昆虫雷达已然实现对迁飞昆虫全天时和全天候的有效监测。当前使用最广泛的昆虫雷达是X波段垂直波束雷达（Vertical-Looking Radar，VLR），其可以实现个体昆虫轨迹、朝向、振翅频率、体重等参数的测量［5-6］，对研究昆虫迁飞行为、害虫监测预警起到了重要作用。然而该型号雷达存在非相参无法测量相位信息、距离分辨率低、极化测量效率低的缺点。为克服当前昆虫雷达的不足，基于现代高分辨全极化雷达技术，新一代Ku 波段高分辨全极化相参昆虫雷达被成功研制［7］，该雷达距离分辨率可达0.2 m，通过同时发射、同时接收两路正交的线极化电磁波，实现目标全极化信息测量［7］，极大提高了目标极化信息测量效率。目前，该雷达已部署在云南、山东、广东等地开展自动化业务运行，成功监测到草地贪夜蛾、黄脊竹蝗等境外重大害虫入侵［8］。

精确的昆虫体重反演对于种类辨识具有重要意义，当前昆虫雷达尚无精准的昆虫种类辨识功能，为确定迁飞昆虫种类，研究人员通常需要将诱虫灯诱捕的昆虫体重与雷达反演的昆虫体重作对比［5］。因此，通过深入分析昆虫雷达散射截面积（Radar Cross Section，RCS）特性实现昆虫体型参数高精度反演是必要的。基于54 只实验昆虫数据，Aldhous 发现昆虫的极化平均RCSa0和极化方向垂直体轴时的RCSSvv与昆虫的体重均存在良好映射关系，并基于此给出了基于a0和Svv反演昆虫体重的经验公式；Chapman 基于112 只昆虫数据改进了基于a0的体重反演方法，将昆虫体重反演下限降低至1 mg；Drake 等人整合了前人的实验数据，进一步提高了基于a0的昆虫体重反演方法的精度，并另外提出精度更高的联合使用a0和α2（记为a0&α2，α2为表示目标极化方向图形状的参数）的体重反演方法［5，9］；胡程等人提出基于昆虫散射矩阵（Scattering Matrix，SM）两个极化不变量v（特征值法）和d（行列式法）的体重反演方法［10-12］，且精度显著高于传统参数a0。此外他们还给出了基于v、d、a0、a0&α2反演昆虫体长和体宽的经验公式［10，12-13］。v的物理意义是极化方向垂直于昆虫体轴时的RCS，d表示极化方向平行和垂直昆虫体轴时RCS乘积的平方根。

到目前为止，v方法和a0&α2方法仍然是估计昆虫体型参数精度最高的两种方法［12］，然而遗憾的是，v和α2的计算以准确判断昆虫类型（即进行平行/垂直昆虫判断，将极化方向平行于体轴时回波强度最大的昆虫定义为平行昆虫，将极化方向垂直体轴时回波强度最大的昆虫定义为垂直昆虫［14］）为前提。胡程等人基于昆虫散射特性发现使用散射矩阵大特征值与小特征值的相对相位符号可以实现平行和垂直昆虫的判别［14］。然而在实际测量中，大量昆虫相对相位接近0°，极化误差极易导致此部分昆虫相对相位符号错误，参数v和α2计算正确率低，从而导致体型参数反演误差增大。d方法虽无须判断昆虫类型，但精度较差。因此，亟需开发反演精度高且无须昆虫类型判别的体型参数反演方法。

本文对暗室测量的157头昆虫极化RCS 特性分析发现，昆虫最小极化RCS与体型参数存在良好映射关系，从而提出基于最小极化RCS的昆虫体型参数反演新方法，该方法无须进行昆虫类型判别。基于微波暗室实测数据对比了新方法与传统v方法、a0&α2方法以及d方法反演体长和体重的精度；基于仿真分析了极化误差对新方法与3种传统方法的影响。

2 昆虫腹部面极化RCS特性

2.1 实验数据

本文将基于9.5 GHz实测昆虫数据分析昆虫的极化RCS特性。所用数据于2018年6～8月和2019年6～7月在北京理工大学微波暗室利用全极化测量装置测量（图1）。全极化测量设备由一台4 端口矢量网络分析仪（型号：R&S®ZVA 40，德国Rohde &Schwarz 公司制造）和2 个双极化天线构成。双极化喇叭天线能同时发射或接收H 和V 极化电磁波。矢量网络分析仪的端口1 和3 分别连接到发射天线的H 和V 极化端口，端口2 和4 分别连接到接收天线的H 和V 极化端口。因而，矢量网络分析仪测量的S 参数S21、S23、S41 和S43 分别对应于HH、HV、VH 和VV 极化信号。测量时收、发天线放置在喇叭的下端口，昆虫体轴与水平极化方向平行，两个天线的轴线相互平行，竖直向上照射昆虫的腹部，实现昆虫腹部面全极化RCS 测量。实验共测量了157只昆虫，体重范围20.2～964 mg，体长范围10.3～47 mm，体宽范围2.2～14 mm。

图1 测量场景Fig.1 Measurement scene

2.2 对称目标的极化方向图表征

全极化雷达可直接测量昆虫HH、HV、VH、VV四个极化通道回波，经过数据处理［7］后可得到昆虫散射矩阵，表示为：

其中，s11、s12、s21、s22分别为HH、HV、VH、VV 通道极化RCS（m2）的平方根，γ、γ′、β分别为对应的相位，对于单基地雷达有s12ejγ=s21ejγ′。

根据式（1）可以计算散射矩阵的两个特征值［10］：

其中，|μ1|和|μ2|表示μ1和μ2的幅度，φ1和φ2表示它们的相位。不失一般性，假设|μ1|≥|μ2|。对于平行昆虫，|μ1|表示极化方向平行于体轴时的RCS平方根，|μ2|表示极化方向垂直于体轴时的RCS 平方根；对于垂直昆虫，|μ1|表示极化方向垂直于体轴时的RCS 平方根，|μ2|表示极化方向平行于体轴时的RCS平方根。

昆虫身体形态通常关于体轴左右对称［15］。对于对称目标，若其体轴平行于H 或V 极化方向，则目标散射矩阵交叉通道为0［16］。假设昆虫关于体轴完全对称，且昆虫为平行昆虫，当昆虫体轴与H 极化平行时，其散射矩阵可以用特征值表示为：

为散射矩阵大特征值与小特征值的相对幅度，命名为差分特征值幅度。根据A的定义不难得到A≥1；φ=arg(μ1/μ2)，为散射矩阵大特征值与小特征值的相对相位，arg（·）表示取相位运算，将φ命名为差分特征值相位。

昆虫的极化方向图表征了不同极化方向下昆虫的RCS，可由散射矩阵计算得到：

其中，θ表示极化方向，σ(θ)表示极化方向为θ时昆虫的RCS。

对称目标的极化方向图关于体轴完全对称。根据极化方向图极值点个数，可将极化方向图分为三种类型［17］：①极化方向图不存在极值点，表示目标RCS 对极化方向不敏感，极化方向图呈现圆形（图2（a））；②极化方向图存在一对极小值点和一对极大值点，极化方向图呈现“8”字形（图2（b））；③极化方向图存在两对极大值和两对极小值，极化方向图呈现“十”字形（图2（c））。

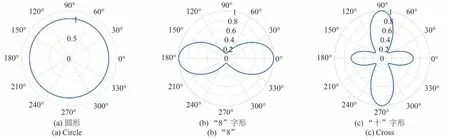
图2 极化方向图类型Fig.2 The type of polarization patterns

2.3 昆虫极化RCS特性分析

为寻找更合适的体型参数估计特征，对昆虫极化RCS特性进行了分析。图3给出了暗室测量四只昆虫的极化方向图，从图3（a）到图3（d），昆虫种类和体重分别为：桃蛀螟（45 mg）、粘虫（234.8 mg）、霜天蛾（530.1 mg）、霜天蛾（935.3 mg）。

图3 四只昆虫极化方向图对比Fig.3 Polarization patterns comparison of four insects

实验测量时，昆虫体轴与水平极化方向平行，因此0°和180°极化方向对应昆虫体轴方向，90°和270°极化方向对应垂直昆虫体轴方向。如图3 所示，随着昆虫体型增大，垂直昆虫体轴RCS 不断增大，这正是文献［10］使用特征参数v估计昆虫体长和体重的原因。进一步分析发现，在昆虫体型增大过程中，除垂直体轴RCS 增大外，最小RCS 也在增大。为验证这一结果，根据式（6），分别计算暗室157头昆虫离散极化方向图σseq，即昆虫在不同极化方向下的RCS序列：

其中，σi表示极化方向为i× 10-1°时昆虫RCS。

然后计算每只昆虫的离散最小极化RCS：

其中，min（·）表示取最小值。

图4 为157 头昆虫离散最小极化RCS与体长和体重的关系。昆虫离散最小极化RCS 与体长和体重都存在较好映射关系，这意味着使用昆虫最小极化RCS可实现对昆虫体型参数估计。

图4 与昆虫体型的关系Fig.4 The relationship between and insect body size

上述分析使用的昆虫离散最小极化RCS 并非昆虫真正的最小极化RCS，为实现基于最小极化RCS 的昆虫体型参数反演，必须得到昆虫最小极化RCS的解析表达。

3 最小极化RCS的解析表达

从极化方向图形状可知，圆形极化方向图各处RCS相等，“8”字形极化方向图RCS最小值即为目标小特征值对应的RCS，“十”字形极化方向图最小值出现在极小值处。因此，须先确定极化方向图形状，再分别求三种极化方向图下昆虫最小极化RCS。

3.1 极化方向图形状判别

下文推导仍以平行昆虫且体轴与水平极化方向平行为假设。据定义，将极化方向图形状判别问题转为σ极值数量判断问题。

A≥1 且A=1 与φ=0 不同时满足，所以有A-cosφ＞0。因此式（10）可转化为：

据定义，“8”字极化形方向图需式（11）恒成立，因此式（11）等价为：

考虑到Acosφ为差分特征值实部，因此上文结论可以整理为：差分特征值实部小于1时，极化方向图为“十”字形，差分特征值实部大于等于1时，极化方向图为圆形或者“8”字形。

注意，上述推导在平行昆虫且体轴与水平极化方向平行的假设下进行。下文证明，体轴与极化方向不平行的平行或者垂直昆虫对于结论同样适用。

平行昆虫的体轴与水平极化方向夹角为ω时，其散射矩阵Sω由S0旋转角度ω得到，即：

其极化方向图σω为：

对比式（6）发现，平行昆虫体轴与水平极化方向夹角为ω时，其极化方向图等效为在θ轴上平移ω个单位（或者说，绕水平极化方向旋转ω），极化方向图形状和大小未发生任何变化。垂直昆虫散射矩阵旋转90°以后，形式和参数大小关系与平行昆虫一致，本质上也是散射矩阵旋转问题，同样不会改变极化方向图大小和形状。因此，上文结论对于非平行昆虫、体轴与水平极化方向呈一定夹角的昆虫都适用。简言之，上文推导和结论完备。

3.2 最小极化RCS计算

确定昆虫极化方向图形状后，接下来分形状计算昆虫最小极化RCSσmin。

对于“8”字形或者圆形极化方向图（Acosφ≥1），σ最小值出现在0或者处，σmin为小特征值对应的RCS：

下文求θ′和σmin。将θ′带入式（9）得：

将式（20）中cos2θ′用1-sin2θ′替换可得：

将式（21）和（22）代入式（6）得：

因此得到σmin的完整表达式：

4 基于最小极化RCS的昆虫体型参数反演

4.1 评价指标

本文使用拟合优度评估回归结果对于体长和体重反演的拟合效果，拟合优度介于0～1，越接近1表明回归曲线对于观测值的拟合效果越好。使用平均相对误差（Mean Relative Error，MRE）来评价估计体长、体重与实测体长、体重的误差。MRE 定义为：

其中，Mi和Ei分别表示估计值和真值，N是样本数量。

4.2 昆虫体型与最小极化RCS的关系

上文已初步验证昆虫最小极化RCS 与体长和体重存在良好映射关系，这一节使用式（24）计算的σmin进一步分析σmin与昆虫体型参数的关系，并给出基于σmin估计昆虫体型参数的方法。σmin与体长和体重的关系如图5 所示，σmin与体重和体长均存在明显正相关关系。如图5（a），在30 mm 以下，σmin和体长存在较好的映射关系，30 mm 以上，σmin与体长关系变差，但整体仍存在映射关系；如图5（b），在全体型段，σmin与体重都存在非常好的映射关系。

图5 σmin与昆虫体型的关系Fig.5 The relationship between σmin and insect body size

将σmin与体长和体重的关系分别用三阶和二阶多项式拟合为：

σmin拟合体重的拟合优度为0.93，MRE为12.18%，拟合体长的拟合优度为0.79，MRE 为13.23%。公式（26）和（27）可以作为利用σmin反演昆虫体长和体重的经验公式，体长反演结果单位为毫米，体重反演结果单位为毫克。将基于最小极化RCSσmin反演体长和体重的方法称为σmin方法。

5 方法对比

5.1 传统特征参数计算

已有文献［10，12］已经证明v和a0&α2是需要昆虫种类先验下反演昆虫体重精度最高的方法，d是不需要任何先验下反演昆虫体重精度最高的方法，因此本文只与v、d、a0&α2方法作对比。

X 波段体型参数反演所用传统参数a0、α2、v、d亦可由目标散射矩阵得到［10］。

a0可以表示为：

α2可以表示为：

5.2 体长反演

特征参数v、d、a0&α2与体长的映射关系如图6所示。v和d与体长均存在较好的映射关系。使用三阶多项式拟合分别拟合体长与v和d，结果如图6（a）和图6（b）中红色曲线所示，拟合关系式为：

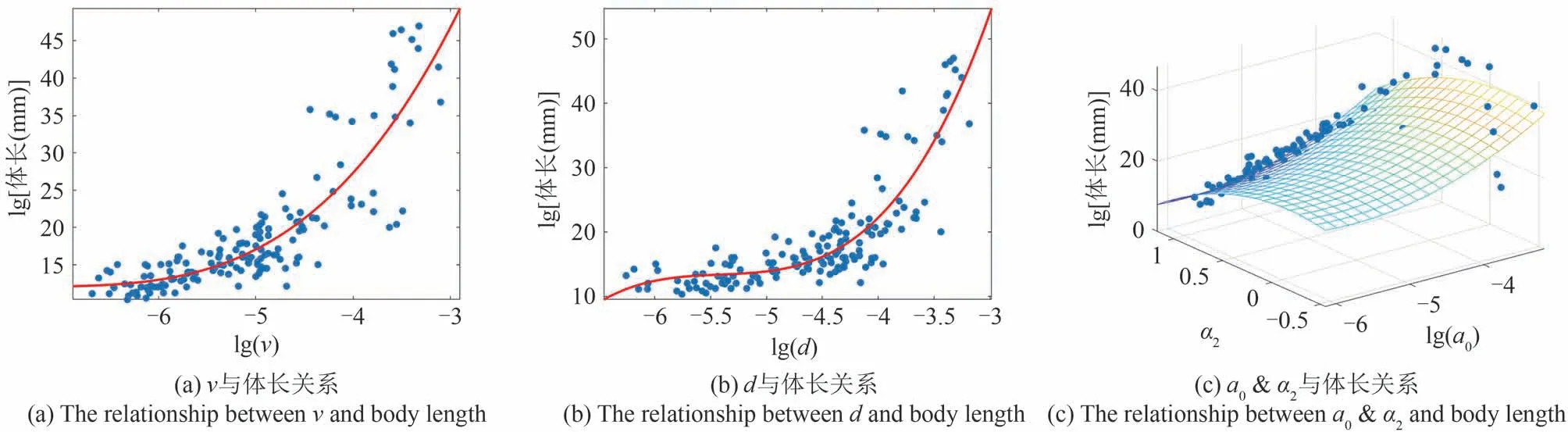
图6 特征参数与体长的关系Fig.6 The relationship between characteristic parameters and body length

其中，lg(v)∈[-6.68，-3.10]，lg(d)∈[-6.26，-3.19]。

如图6（c）所示，a0&α2与体长也存在良好的拟合关系，对于a0&α2，使用二元回归方法拟合，其中a0和α2的拟合阶次均为二阶，拟合结果为：

公式（33）～（35）可作为v、d、a0&α2反演昆虫体长的经验公式。

v方法反演体长的MRE 为13.59%，拟合优度为0.76；d方法反演体长的MRE 为14.20%，拟合优度为0.76；a0&α2方法反演体长的MRE 为15.21%，拟合优度为0.76。为了方便与σmin作对比，表1 给出了四种方法反演体长的对比。结果显示，四种方法拟合体长精度接近，σmin方法精度最高，a0&α2方法精度最差。

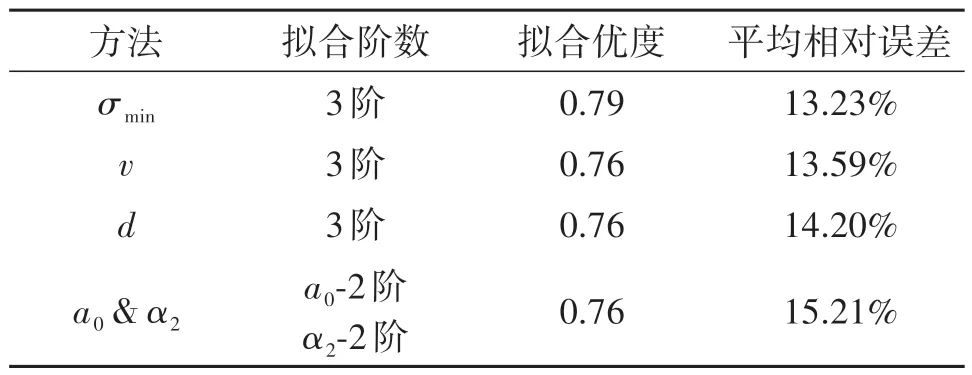
表1 昆虫体长反演方法对比Tab.1 Quantitative comparison of the insect body lengthestimation methods

5.3 体重反演

特征参数v、d、a0&α2与体重的映射关系如图7所示。三者与体重均存在较好的映射关系。使用二阶多项式拟合分别拟合体重与v和d，结果如图7（a）和图7（b）中红色曲线所示，拟合关系式为：

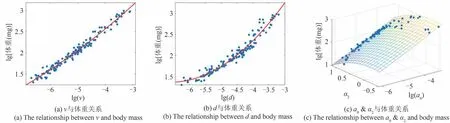
图7 特征参数与体重关系Fig.7 The relationship between characteristic parameters and body mass

使用二元回归拟合a0&α2与体重，其中a0和α2拟合阶数均为二阶，拟合关系式为：

公式（36）～（38）可作为v、d、a0&α2反演昆虫体重的经验公式。

v方法反演体重的MRE为11.54%，拟合优度为0.95；d方法反演体重的MRE 为14.53%，拟合优度为0.91；a0&α2反演体重的MRE为10.97%，拟合优度为0.96。为方便与σmin作对比，表2 同样给出四种方法反演体重精度的对比。结果显示，四种方法反演体重精度接近，a0&α2方法精度最高，d方法精度最差，σmin法精度略差于a0&α2和v方法。

表2 昆虫体重反演方法对比Tab.2 Quantitative comparison of the insect body mass estimation methods

6 极化误差影响仿真

前文已经对比了四种方法反演昆虫体长和体重的精度，对于体长反演，作为无须昆虫类别先验信息的σmin方法精度优于v和a0&α2方法，这是一个令人惊喜的结果。对于体重反演，与前人研究结果类似，需要判断昆虫类型的v方法和a0&α2方法最优，然而根据式（29）和式（31），特征参数v和α2的计算非常依赖于差分特征值相位φ的符号。图8给出了暗室测量昆虫和外场雷达实测昆虫的差分特征值相位分布对比，存在大量目标差分特征值相位接近0。在此情况下，全极化系统通道间相位不一致非常容易造成特征参数v和α2的计算错误，从而导致较大的体型参数反演误差。此外，全极化系统通道间幅度不一致、极化隔离度等极化误差也会对RCS 特征参数的计算产生影响，因此本节将分析系统极化误差对于四种方法精度的影响。

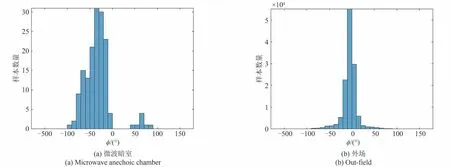
图8 暗室和外场测量昆虫差分特征值相位φ分布Fig.8 φ distribution measured in microwave anechoic chamber and out-field

全极化系统测量得到的昆虫散射矩阵可以表示为［18］：

其中，sij(i，j=h，v)表示理想散射矩阵四个元素；M表示测量得到的散射矩阵，g包含了信号在传输中的增益和衰减，可以通过有效的RCS 定标补偿，且其与散射矩阵差分特征值的计算无关，因此在后边的仿真中假设g=1；ar表示系统H 和V 接收通道间的幅相不一致性；at表示系统H 和V 发射通道间的幅相不一致性；Ci(i=1，2，3，4)表示发射和接收时H 和V 通道间的交叉串扰。Ci(i=1，2，3，4)的值通常较小，我们以课题组研发的高分辨全极化昆虫雷达系统实测极化隔离度为标准，设定Ci(i=1，2，3，4)=-25 dB。

基于此模型，假设收发通道的幅相不一致性相同，以157只昆虫散射矩阵为真值，设置不同的幅相不一致乘到昆虫散射矩阵上，即可仿真不同极化误差下四种方法反演体长和体重的精度。

考虑到在实际系统中，经过有效的极化校准后，系统的极化误差会控制在一定范围内，因此本文仿真时设置的幅度不一致性在正负1.5 dB 以内，相位不一致性在正负15°以内。

首先，仿真相位不一致对四种方法体型反演精度的影响。系统相位不一致设置的变化范围为-15°～15°，系统幅度不一致设置为无误差。相位不一致对四种方法估计体长和体重精度影响的仿真结果如图9 所示，在估计体长和体重时，v方法和a0&α2方法受到相位误差影响最大，特别是当相位误差增大时，随着昆虫类别判别错误率的增加，体长和体重估计的平均相对误差迅速增大，而d方法和σmin几乎不受影响。

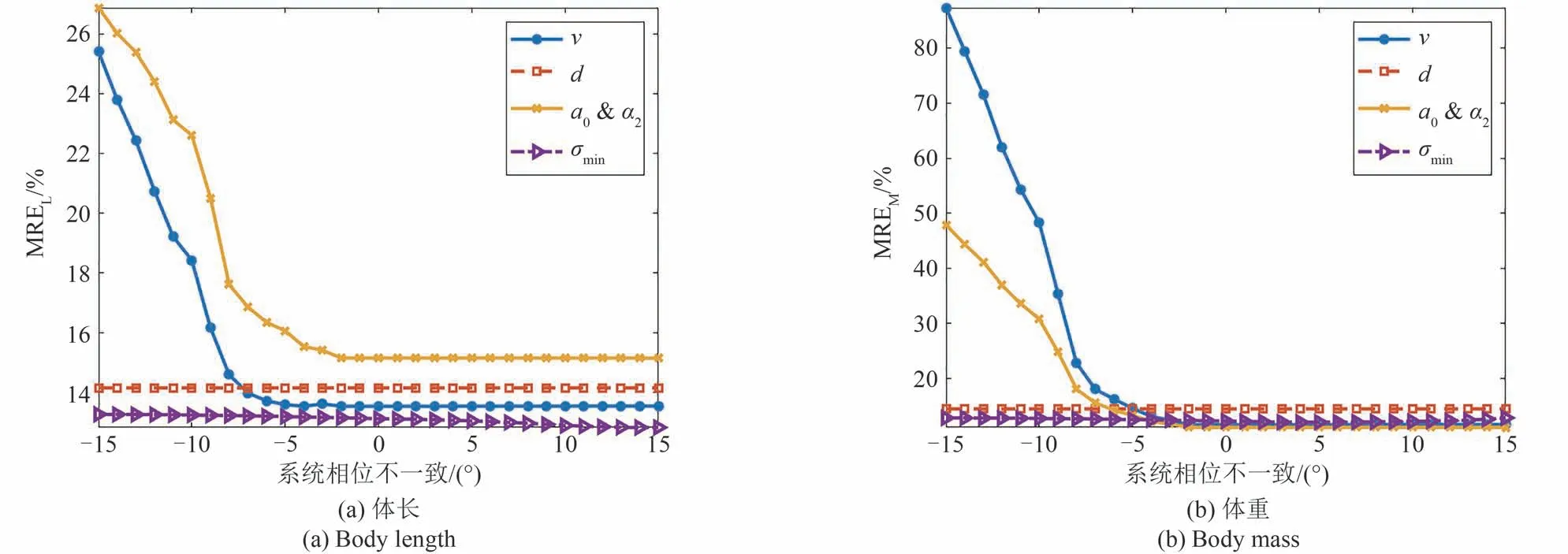
图9 不同相位不一致性下体长和体重估计精度对比Fig.9 Error comparison of insect morphological parameters estimation by four methods at different phase inconsistency

其次，仿真幅度不一致对四种方法体型反演精度的影响。系统幅度不一致设置的变化范围为-1.5 dB～1.5 dB，系统相位不一致设置为无误差。幅度不一致对四种方法估计体长和体重精度影响的仿真结果如图10 所示，在估计体长和体重时，四种方法在不同程度上都受到了幅度误差的影响。其中，在估计体长时a0&α2方法受幅度误差影响最大，其余三个方法所受影响接近；在估计体重时，d方法所受影响最小，其余三种方法所受影响接近，但是在幅度不一致较小的时候，另外三种方法估计体重的精度显然要高于d方法。

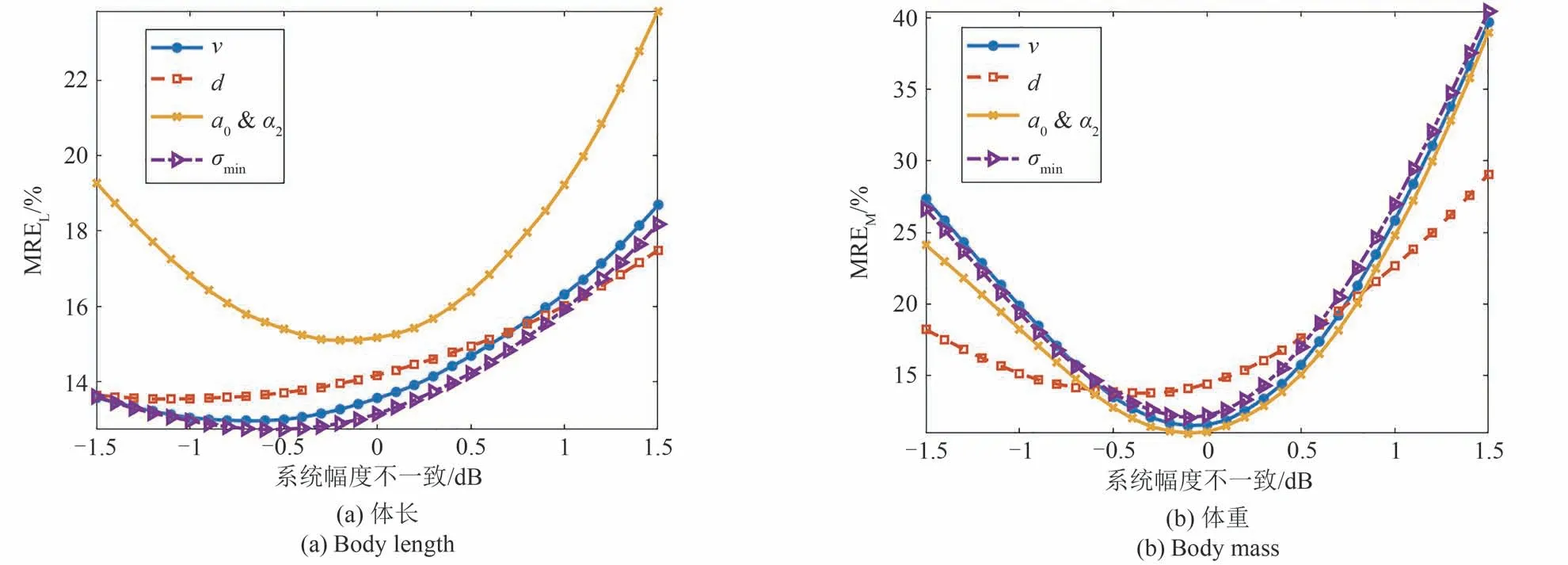
图10 不同幅度不一致下体长和体重估计精度对比Fig.10 Error comparison of insect morphological parameters estimation by four methods at different amplitude inconsistency

以上结果表明，v方法和a0&α2方法抗相位误差性能非常差，d方法和σmin方法几乎不受相位误差影响。a0&α2方法反演体长时抗幅度误差性能差，其余方法抗幅度误差性能接近。

需要注意的是，上述仿真是使用暗室测量的数据进行的，但是从和图8（a）和（b）的对比可知，在实测目标中，差分特征值相位在0°附近的昆虫占比远大于暗室昆虫，因此在实际测量中受相位误差影响的目标会更多，使用v方法和a0&α2方法时反演误差会更大。相对而言d方法和σmin方法抗相位噪声能力强，几乎不受相位误差的影响，且抗幅度误差性能接近。考虑到σmin方法精度更高，在实际使用中σmin方法可能会有更好的性能。

7 结论

本文通过分析昆虫腹部面极化RCS 特性发现昆虫的最小极化RCSσmin与其体长和体重存在较好的映射关系，可以将其作为特征估计昆虫的体长和体重。通过对称昆虫模型，推导了极化方向图形状的判断条件，结果显示当差分特征值实部小于1时，极化方向图为“十”字形，差分特征值实部大于等于1 时，极化方向图为圆形或者“8”字形，并基于此结果推导了昆虫最小极化RCS 的解析表达，从而给出了基于昆虫最小极化RCS 估计体长和体重的经验公式。方法对比显示，σmin方法反演体长精度最高，反演体重精度略低于v方法和a0&α2方法。然而特征参数v和α2的计算需要判断昆虫类型，当昆虫类型判别错误时，会造成计算的特征参数v和α2存在较大误差，从而可能造成较大的体长和体重估计误差。通过仿真分析了极化误差对于四种方法反演精度的影响，结果表明，v方法和a0&α2受极化相位误差影响非常严重，相对而言σmin方法和d方法抗极化误差性能好，几乎不受相位误差的影响。在实际测量中，存在相当数量的昆虫差分特征值相位在0°附近，这必然会造成v方法和a0&α2方法的精度大打折扣，相比而言，抗极化误差性能与d方法接近但精度比d方法高的σmin实用性更好。