多维地震作用下结构的瑞利阻尼系数实用计算方法

徐汉勇, 何泽, 余志武, 李玲瑶

(1.长沙学院 土木工程学院,湖南 长沙 410022; 2.珠海市建筑工程勘察设计院有限公司,广东 珠海 519000; 3.中南大学 高速铁路建造技术国家工程实验室,湖南 长沙 410083)

瑞利阻尼模型广泛应用于结构的抗震计算中,瑞利阻尼系数取值会对瑞利阻尼模型和结构动力响应产生显著影响。因此,国内外学者针对瑞利阻尼系数的计算方法展开了研究。

第一类瑞利阻尼系数的计算方法是通过对结构进行模态分析,提取前若干阶模态,选取任意二阶振型频率作为指定频率,根据瑞利阻尼模型求得的该二阶振型阻尼比与事先假定阻尼比相等的原则确定瑞利阻尼系数。CHOPRA A K[1]、CRUZ C等[2]、ERDURAN E[3]和楼梦麟等[4]指出,该类阻尼系数计算方法只能考虑二阶指定频率对阻尼系数的影响,在应用时,除指定频率外,其余各阶频率对应的阻尼比都存在误差,且指定频率的选择对结构响应影响显著。

第二类瑞利阻尼系数的计算方法是先对结构进行模态分析,提取N阶振型,建立由事先指定的该N阶振型阻尼比、振型阻尼比变化量平方的权重系数、质量瑞利阻尼系数和刚度瑞利阻尼系数表示结构响应变化量平方的表达式,并根据响应误差最小的原则得到阻尼系数优化计算式。相比第一类瑞利阻尼系数的计算方法,第二类计算方法能够考虑多阶频率对阻尼系数的影响,其关键是权重系数的构建与计算。按照响应类别,已有的权重系数计算方法可分为基于节点位移[5-11]、基底剪力[12]和结构整体应变能响应[13-15]3种。按照所采用的方法类别,已有的权重系数计算方法可分为时程分析法[5-9,12-14]、多维组合法[10]和多维虚拟激励法[11,15]3种。按照激励维数,已有的权重系数计算方法可分为基于单维地震激励[5-9,12]和多维地震激励[10-11,13-15]两种。

在已有的第二类瑞利阻尼系数计算方法中,对于由节点位移或基底剪力组成的权重系数,节点序号或位移方向或基底剪力方向的改变,势必会影响阻尼系数的取值,进而影响结构响应。相比之下,结构整体应变能响应不受此影响。同时,作用于实际工程结构的地震激励是多维的。因此,用多维地震激励作用时的结构整体应变能响应构建权重系数更合理,如文献[13-14]。但文献[13-14]中的权重系数计算方法需要先构建以振型频率和振型阻尼比为动力特性的单自由度体系,并计算出该体系在各向地震波作用下的伪速度反应谱。显然,当振型阶次发生变化时,振型频率势必发生改变,致使各向伪速度反应谱也发生变化。以实际工程中常用的塔式结构[16]或大跨空间结构[17]为例,在振型分析时,所取振型数目常在60阶及以上,以使各向振型质量参与系数累计数满足《建筑抗震设计规范》(GB 50011—2010(2016年版))[18](以下简称《规范》)要求,并假设承受三维平动地震激励,在利用文献[13-14]中的权重系数计算方法时,需要利用时间步积分法求得各阶振型对应的3个伪速度反应谱,共计180个及以上伪速度反应谱,计算量略大。文献[15]中构建了多维激励振型参与系数矩阵,并以此提出了计算多维激励应变能响应的虚拟激励法和瑞利阻尼系数计算方法,但计算过程均较复杂。因此,本文在前人研究成果的基础上,先后利用CQC振型组合法和SRSS多维组合法求得应变能响应,并提出应用更方便的瑞利阻尼系数实用计算方法,且以带楼板的多塔结构和不带楼板的空间结构为例,对瑞利阻尼系数实用算法、文献[13-14]算法和文献[15]算法求得的节点位移和杆件内力进行对比分析。应注意的是,在已有瑞利阻尼系数优化计算方法中[5-15],均以利用基于事先拟定振型阻尼比的振型分解法求得的结构响应为标准,本文也以此来确定标准。

1 SRSS多维组合应变能响应计算

(1)

取前N阶振型,记φi为第i阶振型的节点位移幅值向量,qi(t)为位移振型坐标,根据振型叠加原理和振型正交规则,得平衡方程为:

(2)

利用式(2)求得qi(t),并得到结构在x向地震激励下的应变能时程响应Wx(t)为:

(3)

式中:φj为第j阶振型的节点位移幅值向量;qj(t)为第j阶位移振型坐标。

利用振型正交性,可将式(3)变为:

(4)

式中Ei为第i阶振型应变能。

(5)

对于非隔震土木工程结构,常用材料阻尼比较小,根据文献[19],可得振型坐标qi(t)最大值为:

(6)

将式(6)代入式(4)的累加项,可得累加项最大值。应注意的是,式(4)中累加项值仅取决于相应单阶振型。因此,可将累加项最大值看作相应单阶振型对应的最大应变能Eimax,

(7)

在式(7)基础上,只需利用振型组合方式便可求得单维地震激励作用下的应变能响应值。按照《规范》给出的CQC振型组合方式,得到x向地震激励单独作用时的结构应变能响应Wx:

(8)

式中:ρij为振型相关系数[18];Ejmax为第j阶振型对应的最大应变能;Ej为第j阶振型应变能;rxj为沿x向第j阶振型参与系数;axj为第j阶振型对应的地震影响系数;ωj为第j阶振型圆频率。

类似式(8),可分别求得y向和z向地震激励单独作用下的应变能响应Wy和Wz:

(9)

(10)

式中:ryi、ryj分别为第i阶振型和第j阶振型的y向振型参与系数;rzi、rzj分别为第i阶振型和第j阶振型的z向振型参与系数;ayi、azi分别为以第i阶振型频率和振型阻尼比为特性的单自由度体系对应的水平y向和竖直z向地震影响系数,其中ayi与axi相等。

当考虑多维地震激励作用时,根据SRSS多维组合法规则,可得结构应变能响应W的平方为:

(11)

2 瑞利阻尼系数实用计算方法

按照瑞利阻尼模型构造原理,阻尼矩阵C[1]为

C=αM+βK。

(12)

式中:α为质量阻尼系数;β为刚度阻尼系数。

文献[6-7]构建了结构响应变化量Qk与瑞利阻尼系数的优化方程:

(13)

提取式(11)的后面累加项,可得

(14)

则

(15)

(16)

(17)

(18)

(19)

3 工程案例

3.1 塔式结构

相比文献[13-14],式(8)—(19)所示的瑞利阻尼系数实用计算方法不需要计算各向地震波各阶振型对应的伪速度反应谱,只需结合《规范》给出显式曲线来计算地震影响系数。相比文献[15],该计算过程简单,且SRSS多维组合法是在工程实践中得到认可的计算方法。为进一步说明各类阻尼系数计算方法的差异,分别以常用的带楼板钢筋混凝土塔式结构和不带楼板的K8单层球面网壳结构作为案例进行分析。

塔式结构如图1所示,底盘一层,塔楼1与塔楼3、塔楼2与塔楼4在几何位置、构件几何尺寸和材料强度等方面都满足水平双向对称要求。记各塔楼各层楼面质量分别为M1、M2、M3和M4,构建比值为1∶1∶1∶1的水平双向对称、1∶1∶2∶1的水平单向偏心以及1∶1∶2∶2和1∶1∶2∶4的水平双向偏心多塔结构。利用ANSYS软件构建有限元模型,用beam4单元模拟梁柱,用shell63单元模拟楼板,进行模态分析和提取振型参与质量比值。选取了水平双向对称(1∶1∶1∶1)和水平双向偏心(1∶1∶2∶4)最显著的多塔结构进行分析,结果如图2所示。

图1 四塔结构

由图2可知,无论对于带楼板的双向对称多塔结构,还是对于带楼板的双向偏心多塔结构,各向多阶振型参与质量显著不为零,尤其是水平双向偏心结构更显著。

3.2 空间网壳结构

K8单层球面网壳结构如图3所示,所有环向构件、径向构件采用的材料强度、几何尺寸以及底部支座约束均满足球对称条件。假设球面质量集中分布在构件交点上,并按照集中质量大小将球面分成4个区域,集中质量分别记为M1、M2、M3和M4,构建1∶1∶1∶1的水平双向对称、1∶2∶1∶1和1∶1∶2∶1的水平单向对称和1∶2∶3∶4的水平双向偏心的空间结构。利用ANSYS有限元软件的beam4单元模拟环向和径向构件,mass21模拟集中质量点,建立数值模型,并进行模态分析和提取前100阶振型的振型参与质量比值。选取了水平双向对称(1∶1∶1∶1)和水平双向偏心(1∶2∶3∶4)的网壳结构进行分析,结果如图4所示。

图3 K8单层球面网壳质量分布

图4 K8单层球面网壳结构振型参与质量比值分布

由图4可知,不带楼板的双向对称和双向偏心K8单层球面网壳结构,多阶振型的参与质量也显著大于零,偏心结构更显著。

4 算法比较

假设各类塔式结构和各类K8单层球面网壳结构均位于Ⅱ类场地,设计基本地震加速度为0.10g,抗震设计分组为两组。根据该地震环境,并结合《规范》,可绘制出动力系数反应谱曲线。依据动力系数反应谱曲线相似的原则,确定了Kobe波和Taft波的动力系数反应谱曲线,如图5所示。

图5 动力系数反应谱曲线的比较

4.1 塔式结构比较

按照文献[13-14]算法、文献[15]算法,以及本文提出的瑞利阻尼系数实用计算方法的计算过程,并结合MATLAB软件规则,编制各算法对应的计算程序。对于各钢筋混凝土塔式结构,根据《规范》,各振型阻尼比可拟定为0.05,利用各阻尼系数算法的计算程序求得相应质量阻尼系数α和刚度阻尼系数β(×10-3),结果见表1。对于文献[13-14]算法,表中给出了各塔楼在Taft波作用下得到的阻尼系数。表中塔1、塔2、塔3和塔4分别表示M1∶M2∶M3∶M4为1∶1∶1∶1、1∶1∶2∶1、1∶1∶2∶2和1∶1∶ 2∶4的塔式结构。

表1 基于不同算法的塔式结构阻尼系数的比较

以基于拟定振型阻尼比求得的结构三维平动地震激励时程响应最大值为标准,对基于各阻尼系数算法求得的结构时程响应最大值进行比较。响应包括节点位移和杆件内力,节点为各结构塔楼1左下角第1列柱的13个节点,并选取该列柱的12根杆件。图6给出了塔1和塔4的响应误差比较结果,并按照文献[13-14]阻尼系数算法,给出了图7所示的以塔4结构前60阶振型频率和振型阻尼为特性的单自由度体系在三维Kobe地震波作用下的伪速度反应谱。

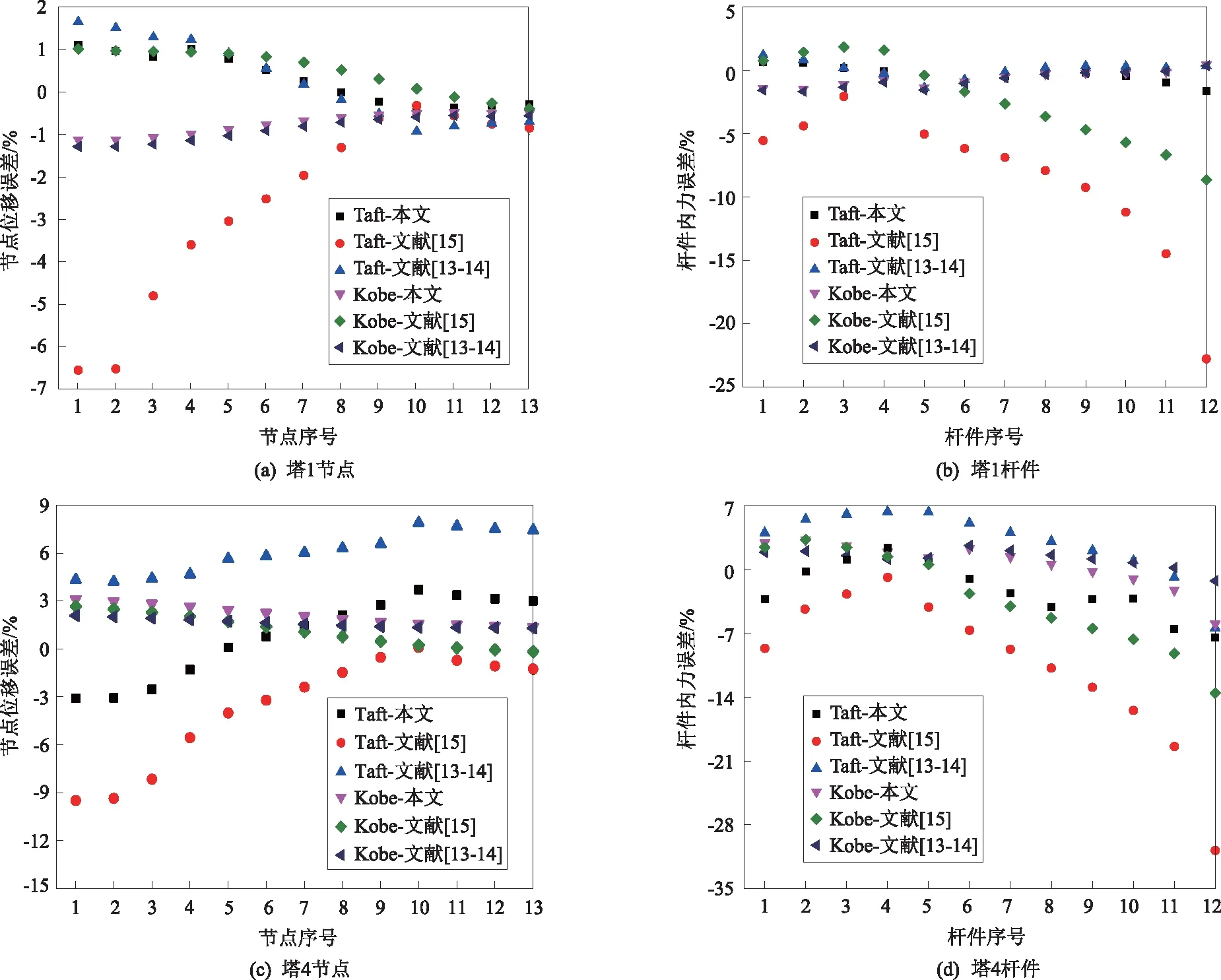
图6 在Taft、Kobe两种地震波作用下基于不同算法的塔式结构响应误差比较

图7 三维Kobe地震波作用下的伪速度反应谱

由图6可知,对于塔式结构,基于本文瑞利阻尼系数实用算法得到的节点位移误差和杆件内力误差与基于文献[13-14]算法得到的误差相差不大,但明显小于基于文献[15]算法得到的误差。这是由于塔楼底盘的强连接作用,致使局部塔的振动引起其他位置塔的振动,表现为该类结构的空间作用显著。而本文瑞利阻尼系数实用算法和文献[13-14]算法本质上都是基于SRSS多维组合法,文献[15]算法中的系数矩阵缺乏足够的理论依据,致使该算法并不是基于SRSS多维组合法。此外,按照文献[13-14]的计算方法,需要构建以振型频率和振型阻尼比为动力特性的单自由度体系,并求得该体系在各向地震激励作用下的各向伪速度反应谱。显然,当振型阶次发生变化时,振型频率也随着改变,各向伪速度反应谱也发生变化(图7)。本文选取了两条三维地震波,取了前60阶振型,文献[13-14]算法需要采用时间积分步法计算360个伪速度反应谱,而本文的实用算法只需直接利用《规范》中的公式计算240个地震影响系数。因此,计算效率更高,应用更方便。

4.2 空间网壳结构

拟定各类K8单层球面网壳结构各阶振型阻尼比为0.02,表2给出了利用各类阻尼系数算法求得的质量阻尼系数α和刚度阻尼系数β(×10-3),表中的壳1、壳2、壳3和壳4分别表示质量比M1∶M2∶M3∶M4分别为1∶1∶1∶1、1∶2∶1∶1、1∶1∶2∶1和1∶2∶3∶4的K8网壳结构,对于文献[13-14]算法,表中给出了各网壳结构在Kobe波作用下得到的阻尼系数。

表2 基于不同算法的K8单层球面网壳阻尼系数比较

选取球面第1环的8个节点和该环的8根杆件进行计算,图8给出了壳1、壳4节点位移误差和杆件内力误差的比较结果。

图8 在Taft、Kobe两种地震波作用下基于不同算法的K8单层球面网壳响应误差比较

由图8可知,对于网壳结构,基于本文瑞利阻尼系数实用算法、文献[13-14]算法和文献[15]算法求得的节点位移误差和杆件内力误差均较小,未出现类似塔式结构误差显著的现象。其原因为网壳结构杆件之间没有通过钢筋混凝土楼板相连,理论上局部振动可以是独立的。此外,在利用文献[13-14]算法时,取了前100阶振型,累计求得600个伪速度反应谱,在用本文实用算法时,累计求得400个地震影响系数。

5 结论

1)结合应变能响应计算公式和SRSS多维组合法,构建了振型阻尼比变化量平方的新型权重因子,并提出了能合理考虑多阶振型和多维地震作用对结构响应影响的瑞利阻尼系数实用计算方法。

2)基于瑞利阻尼系数实用计算方法得到的带楼板塔式结构和不带楼板网壳结构的地震响应误差均较小,且相比已有基于应变能响应的瑞利阻尼系数计算方法,计算过程更简便,应用更方便。